图像处理 傅里叶正逆变换与余弦正逆变换 【附C++实现】
一点说明
1. 完成情况
- 傅里叶变换(DFT)与余弦变换(DCT)
- 快速傅里叶变换(FFT)与快速傅里叶逆变换(IFFT)
- 快速余弦变换(FCT)与快速余弦逆变换(IFCT)
2. 项目结构
- root/
- bin/(存放可执行文件,双击直接运行)
- src/(存放项目源代码,编译需要先配置OpenCV)
- Photos/(存放图片样例,包括原图与变换后的图片)
- Data/(存放图像变换生成的数据,如幅度值与相位值)
- README.md(技术分析报告)
思路分析
1. 傅里叶变换
利用二维的傅里叶变换,我们可以将图像信号从空间域(spatial domain)变换到其对应的频域(frequency domain)中进行分析,这与我们日常观察世界的视角是截然不同的。
所谓傅里叶变换其实是正交变换的一种,其原理是“周期与非周期信号都可用正弦函数的加权积分表示”。在图像处理中,我们一般用到的是二维离散傅里叶变换,具体公式如下。
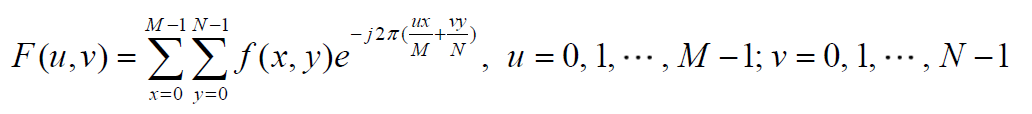
在具体的编码实现时,我们常常利用欧拉变换将公式中的实部与虚部分离(如下图)。
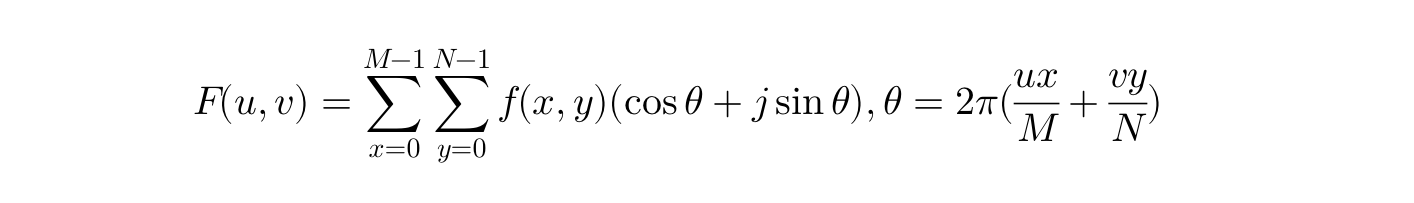
可以发现, 通过上述变换,我们将二维离散傅里叶变换的公式由\(F(u,v)=|F(u,v)|e^{jφ(u,v)}\)的形式转化成了\(F(u,v)=R(u,v)+jI(u,v)\)的形式,所以有下式。
上式中的 \(φ(u,v)\)为图像信号在\((u,v)\)点的幅度值,\(|F(u,v)|\)为信号在\((u,v)\)点的相位值。通过上面的拆分,我们可以轻松地编写程序进行计算,得到所谓的幅度图像和相位图像。其中幅度图像包含了我们所需要的图像几何结构的所有信息,在图像分析和处理中应用最为广泛。
2. 余弦变换
余弦变换也是正交变换的一种。由前面提到的傅里叶变换公式可以知道,偶函数的傅立叶变换的虚部为零,因而不需要计算,只计算余弦项变换,这就是余弦变换 。显然,余弦变换的变换核为实数的余弦函数(公式如下),其计算速度相比傅里叶变换要快得多,所以余弦变换被广泛应用于图像有损压缩和语音信号处理等众多领域。
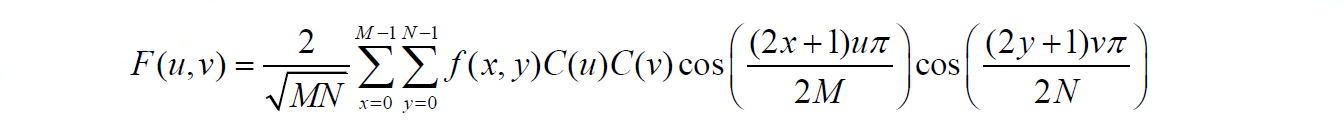
3. 逆变换
可以证明,傅里叶变换与余弦变换都是可逆的,其逆变换公式可以通过矩阵的逆运算性质求出,具体公式如下。
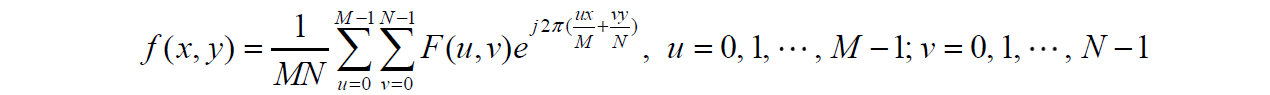
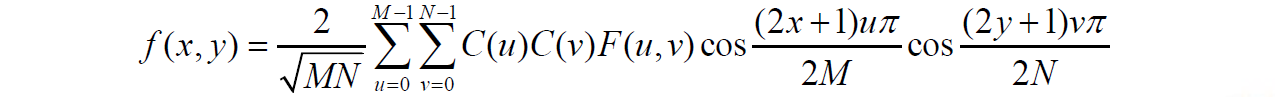
4. 快速变换
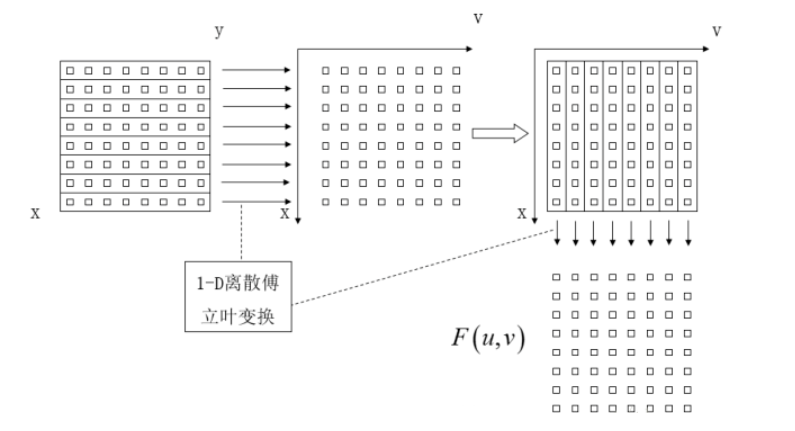
无论是快速傅里叶变换还是快速余弦变换,其实都是利用了变换的可分离性,借助动态规划的思想,将二维离散变换的复杂度从 \(O(n^2)\) 优化到 \(O(nlogn)\) 。基本思路如下图所示(图源博客)。
关键代码
此处仅贴出了快速傅里叶正逆变换(FFT&IFFT)与快速余弦正逆变换(FCT&IFCT)等关键代码,其他代码如简单离散傅里叶变换(DFT)与余弦变换(DCT)的代码请见附件。
1. 主函数与主要参数
constexpr auto AMAX = 100; //调整幅度值可视化参数
constexpr auto CMAX = 50; //调整余弦变换可视化参数
//可选的照片:"photo" "Gundam" "lena"
static String name = "Gundam";
//将图像存储容器中的值映射到[0,255]的灰度区间内
enum StandardType
{
AMPLITUDE, //幅度图
PHASE, //相位图
COSINE, //余弦变换图
SIFFT, //傅里叶逆变换
SIFCT //余弦逆变换
};
int Shift(Mat& src, Mat& dst); //中心化
int Standard(Container src, Mat& dst, int type); //映射到[0,255]区间
int DFT(Mat src, Container& A, Container& φ); //二维离散傅里叶变换
int DCT(Mat src, Container& C); //二维离散余弦变换
int FFT(Mat src, Container& R, Container& I, Container& A, Container& φ); //快速傅里叶变换
int FCT(Mat src, Container& C); //快速余弦变换
int IFFT(Container R, Container I, Mat& dst); //快速傅里叶逆变换
int IFCT(Container& C, Mat& dst); //快速余弦逆变换
2. 快速傅里叶变换
int FFT(Mat src, Container& R, Container& I, Container& A, Container& φ) {
double M = src.rows; double N = src.cols;
for (int v = 0; v < N; v++) {
vector<double> listR, listI;
for (int x = 0; x < M; x++) {
double r = 0.0, i = 0.0;
for (int y = 0; y < N; y++) {
double t = -2 * PI * v * y / N;
r += src.ptr<uchar>(x)[y] * cos(t);
i += src.ptr<uchar>(x)[y] * sin(t);
}
listR.push_back(r);
listI.push_back(i);
}
for (int u = 0; u < M; u++) {
double r = 0.0, i = 0.0;
for (int x = 0; x < M; x++) {
double t = -2 * PI * u * x / M;
r += listR[x] * cos(t) - listI[x] * sin(t);
i += listR[x] * sin(t) + listI[x] * cos(t);
}
R[u].push_back(r); I[u].push_back(i);
A[u].push_back(sqrt(r * r + i * i));
φ[u].push_back(atan(i / r));
}
}
return 0;
}
3. 快速余弦变换
int FCT(Mat src, Container& C) {
for (int v = 0; v < N; v++) {
vector<double> list;
for (int x = 0; x < M; x++) {
double c = 0.0;
for (int y = 0; y < N; y++) {
double t = (2.0 * y + 1.0) * v * PI / (double)(2.0 * N);
t = (double)src.ptr<uchar>(x)[y] * cos(t);
if (v == 0) t /= sqrt(2);
c += t;
}
list.push_back(c);
}
for (int u = 0; u < M; u++) {
double c = 0.0;
for (int x = 0; x < M; x++) {
double t = (2.0 * x + 1.0) * u * PI / (double)(2.0 * M);
t = list[x] * cos(t);
if (u == 0) t /= sqrt(2);
c += t;
}
C[u].push_back(c * 2 / sqrt(M * N));
}
}
return 0;
}
4. 快速傅里叶逆变换
int IFFT(Container R, Container I, Mat& dst) {
double M = dst.rows; double N = dst.cols; Container Cdst(M);
for (int v = 0; v < N; v++) {
vector<double> listR, listI;
for (int x = 0; x < M; x++) {
double r = 0.0, i = 0.0;
for (int y = 0; y < N; y++) {
double t = 2 * PI * v * y / N;
r += R[x][y] * cos(t) - I[x][y] * sin(t);
i += R[x][y] * sin(t) + I[x][y] * cos(t);
}
listR.push_back(r);
listI.push_back(i);
}
for (int u = 0; u < M; u++) {
double ifft = 0.0;
for (int x = 0; x < M; x++) {
double t = 2 * PI * u * x / M;
ifft += listR[x] * cos(t) - listI[x] * sin(t);
}
Cdst[u].push_back(ifft / (M * N));
}
}
Standard(Cdst, dst, SIFFT);
return 0;
}
5. 快速余弦逆变换
int IFCT(Container& C, Mat& dst) {
double M = dst.rows; double N = dst.cols; Container Cdst(M);
for (int v = 0; v < N; v++) {
vector<double> list;
for (int x = 0; x < M; x++) {
double c = 0.0;
for (int y = 0; y < N; y++) {
double t = (2.0 * y + 1.0) * v * PI / (double)(2.0 * N);
t = C[x][y] * cos(t);
if (v == 0) t /= sqrt(2);
c += t;
}
list.push_back(c);
}
for (int u = 0; u < M; u++) {
double c = 0.0;
for (int x = 0; x < M; x++) {
double t = (2.0 * x + 1.0) * u * PI / (double)(2.0 * M);
t = list[x] * cos(t);
if (u == 0) t /= sqrt(2);
c += t;
}
Cdst[u].push_back(c * 2.0 / sqrt(M * N));
}
}
Standard(Cdst, dst, SIFCT);
return 0;
}
结果展示
1. 基本展示
从左到右依次为 原图 - 幅度图 - 余弦变换图 - 相位图



2. 傅里叶变换
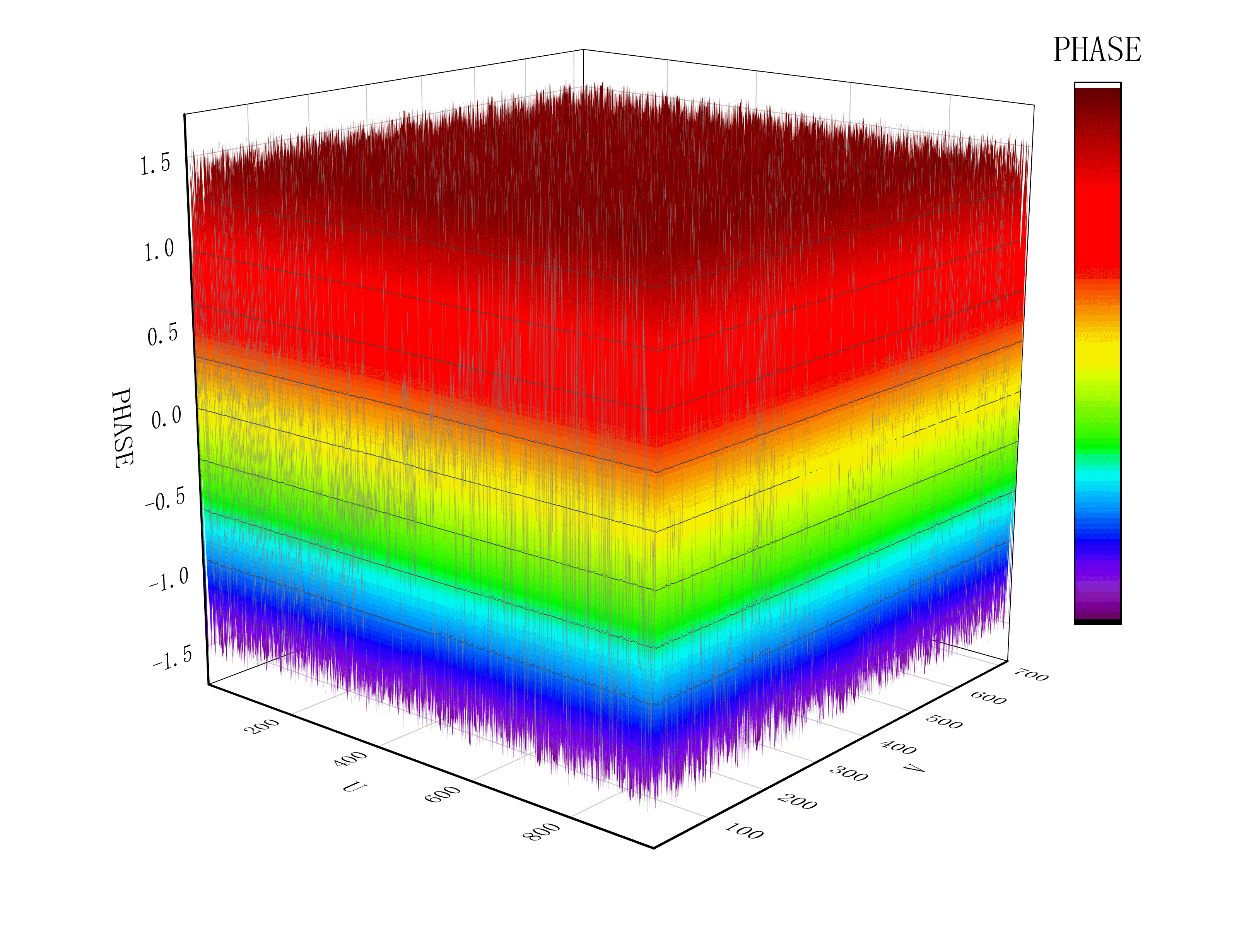
为了更好的展示两种变换的特点,避免将数据映射到[0,255]灰度区间所带来的数据丢失,我在三维空间坐标系中重新绘制了幅度图与相位图,如下图所示。
(1)幅度图
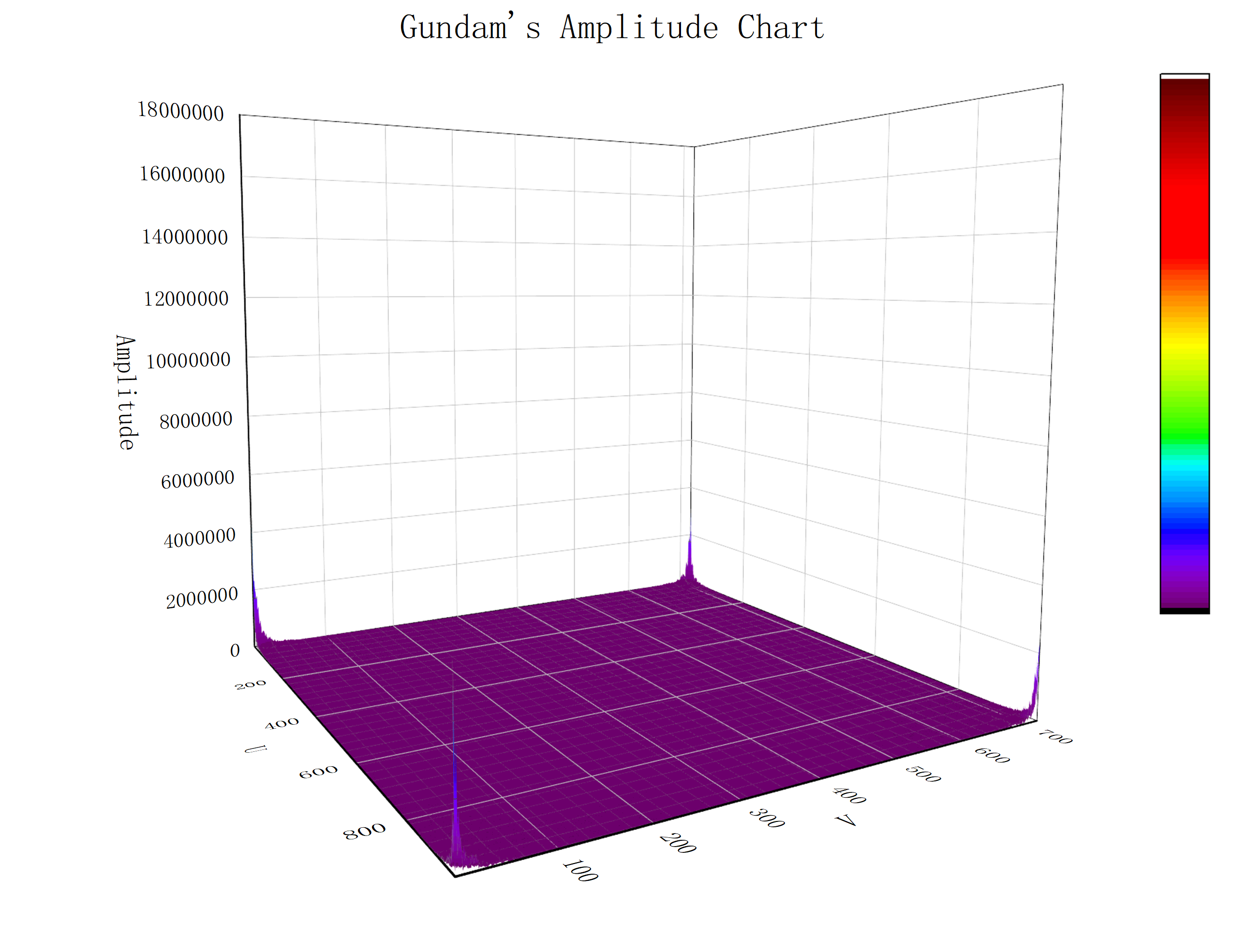
(2)中心化以后的幅度图
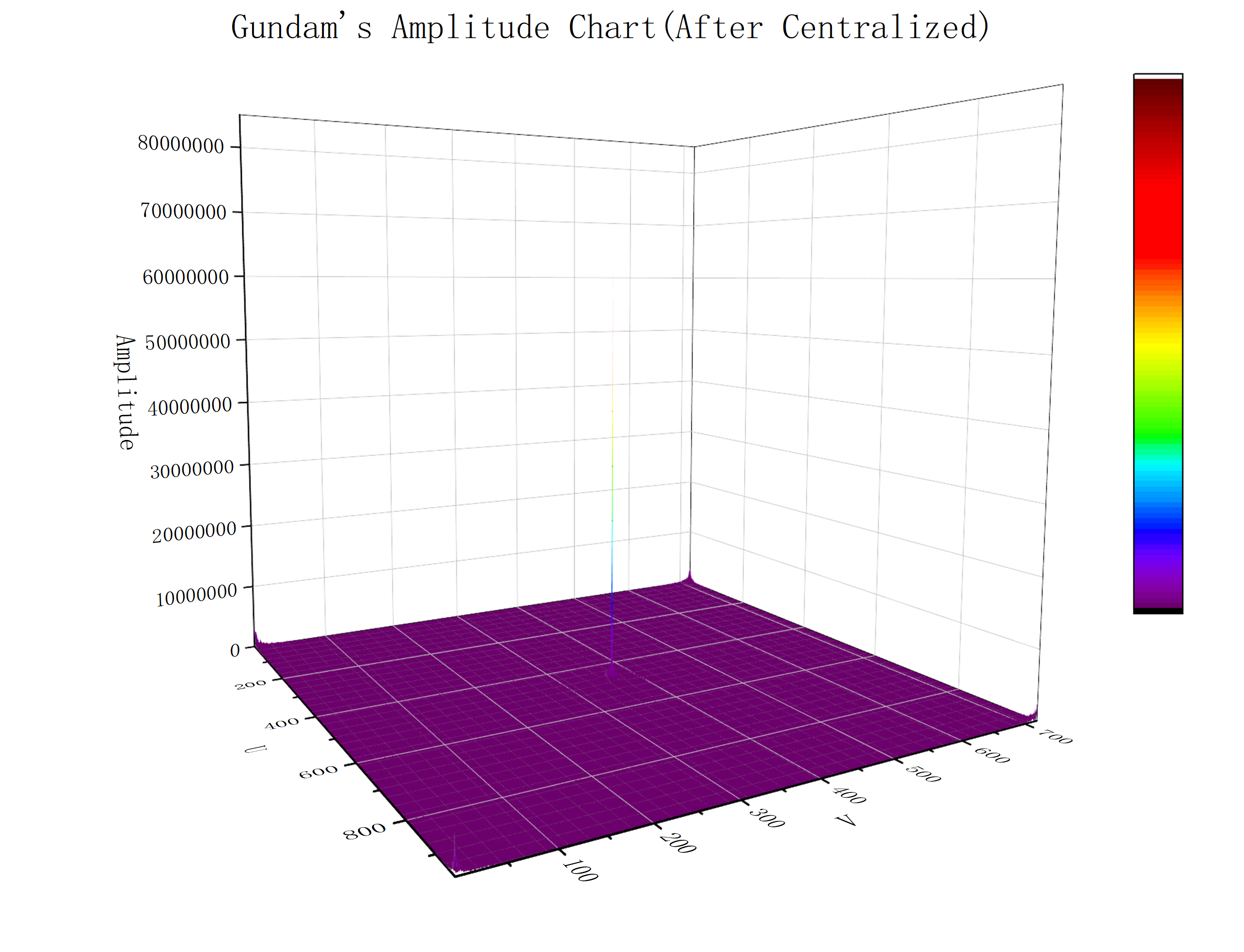
(3)相位图
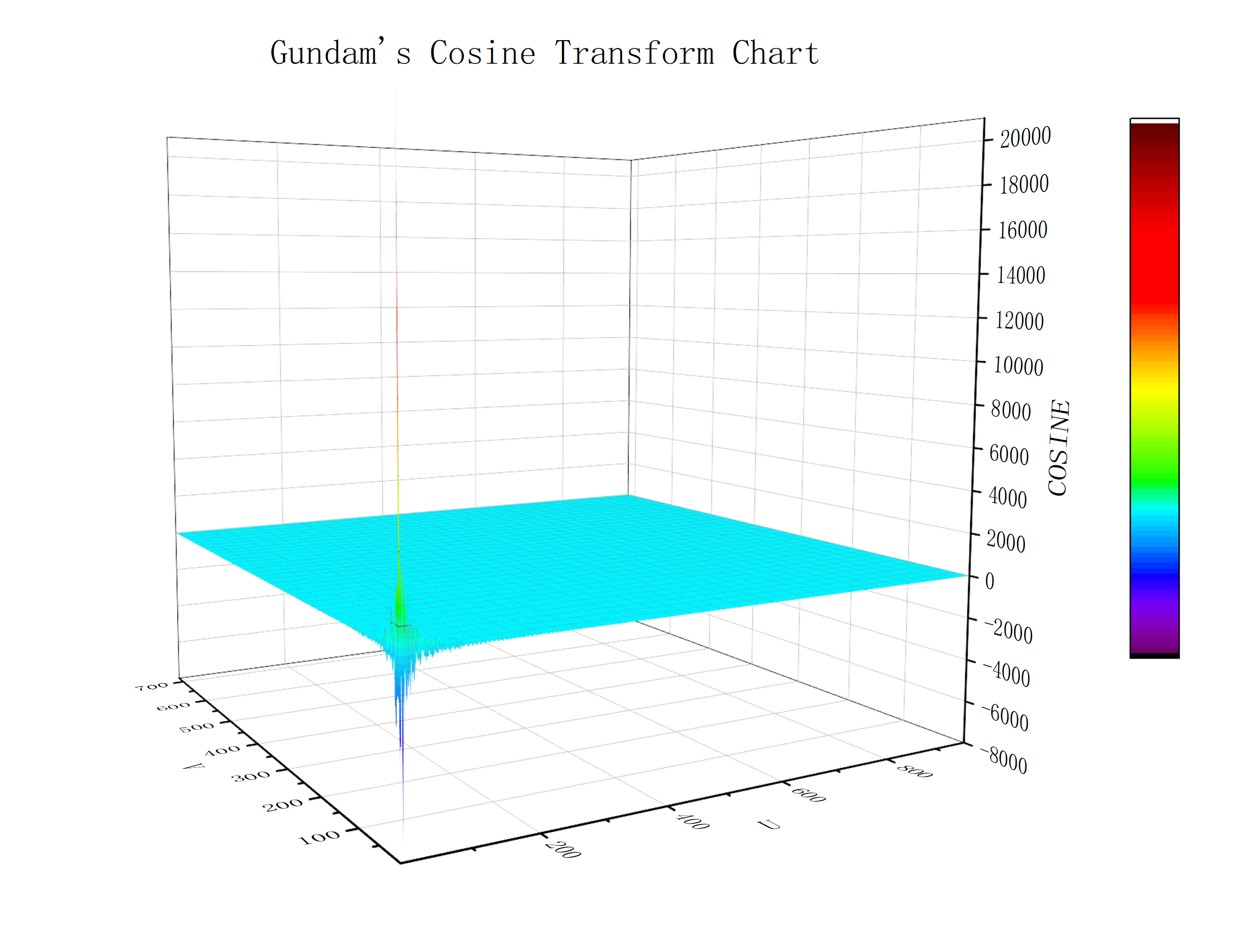
2. 余弦变换
从下图我们可以看出,余弦变换后图像信号的能量集中于一角,这是余弦变换最显著的特点。
作业小结
- 本次作业使用C++语言进行编写,在编写过程中,数字精度的控制给我造成了很大的困扰;
- 映射到[0,255]灰度区间时不同映射函数的选择也给我带来了很大的麻烦,最后我为不同的图像设置了不同的映射函数,通过枚举变量作为参数进行选择;
- 一直没有找到合适的可视化方法,直到 Origin 出现在我的面前;
- 傅里叶变换与余弦变换的原理掌握还不够透彻,需要进一步理论的加强;
- 本想要做滤波等傅里叶变换的实际应用,但终是没有时间,下次一定,下次一定!

