拟阵学习笔记

• 定义：\(M=(S,\mathcal{I})\) 表示一个定义在有限集 \(S\)，独立集的集合是 \(\mathcal{I}\) 的拟阵，其中 \(\mathcal{I}\subseteq 2^S\)
  即 \(\mathcal{I}\) 是 S 中一些子集构成的集合

• 公理：\(I\in \mathcal{I},J\subseteq I\to J\in \mathcal{I}\)
  \(I,J\in \mathcal{I}\)，且 \(|J|>|I|\)，那么存在 \(z\in J/I\)，满足 \(I\cup z\in \mathcal{I}\)

• 基与环：对于一个独立集 \(I\)，若 \(I\) 加上任意一个 \(S/I\) 中的元素都会变成非独立集，那么 \(I\) 是拟阵的一个基
  对于 \(I\) 若去掉 \(I\) 中任意一个元素都会变成独立集，那么 \(I\) 是一个环
  对于一个拟阵，所有基大小相同（有扩张性得知）

• 秩函数：基的元素个数称为拟阵的秩，用 \(r(U)\) 表示 U 中极大独立集的大小

• 拟阵上的最优化（例如无向图最小生成树）
  

• 拟阵交问题：
  给出两个矩阵 \(M_1,M_2\)，要找到一个 \(I\) 满足在两个拟阵中都为独立集，最大化 \(I\)，或最大化 \(\sum_{e\in I}w_e\)
  下面介绍拟阵交算法
  我们先介绍关键的最大最小定理：\(max_{I\in \mathcal{I}_1\cap \mathcal{I}_2}|I|=min_{U\subseteq S}(r_1(U)+r_2(S/U))\)
  首先 \(|I|=|I\cap U|+|I\cap (S/U)|\le r_1(U)+r_2(S/U)\)
  我们在拟阵交算法的过程中会给出取等的构造，容易发现构造出来了取等条件就找到了最优解

• 定义 \(A\) 的闭包算子 \(cl(A)=\{e\in S\mid r(A\cup \{e\})=r(A)\}\)
  性质：\(A\subseteq B\to cl(A)\subseteq(cl(B))\)
  \(e\in cl(A),cl(A\cup \{e\})=cl(A)\)，\(cl(A)=cl(cl(A))\)

• 强基交换定理：对于拟阵 \(M\) 和两个不同的基 \(A,B\)，对于任意元素 \(x\in A/B\)，都存在 \(y\in B/A\)，使得 \(A-\{x\}+\{y\}\) 和 \(B-\{y\}+\{x\}\) 都是基
  证明：\(B\) 是基 \(\to\) \(B+\{x\}\) 包涵一个唯一的环 \(C\)，且 \(x\in C\)，即 \(x\in cl(C-\{x\})\to x\in cl((A\cup C)-\{x\})=cl(A\cup C)\)
  又有 \(S=cl(A)\subseteq cl(A\cup C)=cl((A\cup C)-\{x\})\)，所以 \((A\cup C)-\{x\}\) 有一个基，设其为 \(A'\)，有 \(|A'|>|A-\{x\}|\)，故必定存在 \(y\in A'/(A-\{x\})\) 使得 \(A-x+y\) 是基
  又 \(A'/(A-x)\subseteq (A\cup C-x)/(A-x)\subseteq C-x\)，所以存在 \(y\in C-x\) 使得 \(A-x+y\) 是基，由 \(C\) 是环知 \(B-y+x\) 也是基

• 拟阵交算法：这个算法定义在一种叫交换图的二分图上
  对于拟阵 \(M\) 和一个独立集 \(I\)，定义 \(M\) 中 \(I\) 的交换图 \(D_M(I)\) 如下：
  有 \(I,S/I\) 两部点构成，一条连接 \(y\in I,x\in S/I\) 的边存在，当且仅当 \(I-y+x\in \mathcal{I}\) 成立
  性质：
  令 I，J 都为独立集，且 \(|I|=|J|\)，那么在 \(D_M(I)\) 中存在一个关于 \(I/J\) 和 \(J/I\) 的完美匹配
  证：不妨令 \(I,J\) 都是基，由强基交换定理：取 \(x\in I/J\)，存在 \(y\in J/I\)，使得 \(I-x+y\) 为独立集
  那么一定存在 \((x,y)\) 的一条边，将这条边匹配，然后令 \(I:=I-x+y,J:=J-y+x\)，继续匹配
  令 I 为独立集，\(|I|=|J|\)，若存在唯一的 \(I/J,J/I\) 的完美匹配，那么 J 也是独立集
  证：我们先将点排好序，\(I/J\) 的点 \(x_i\) 只能向 \(J/I\) 中 \(y_j(j\ge i)\) 的点连边
  假设 J 存在环 \(C\)，取最大的 \(y_i\) 满足 \(y_i\in C\)，由于是最大的，所以 \(C-y_i\subseteq cl(I-x_i)\)（\(x_i\) 只向后面的点连了边）
  故 \(cl(C-y_i)=cl(I-x_i)\)，所以 \(y_i\in cl(I-x_i)\) 这和交换图的定义矛盾

• 给定两个拟阵 \(M_1,M_2\)，和 \(I\in \mathcal{I}_1\cap \mathcal{I}_2\)
  定义一个二部图，两边的点是 \(I,S/I\)，一条边 \(y\in I,x\in S/I\) 存在，当且仅当 \(I-y+x\in \mathcal{I}_1\)，
  一条边 \(x\in S/I,y\in I\) 存在，当且仅当 \(I-y+x\in \mathcal{I}_2\)

• 算法流程：
  令初始 \(I\) 为空，定义 \(X_1=\{x\notin I\mid I+x\in \mathcal{I}_1\},X_2=\{x\notin I\mid I+x\in \mathcal{I}_2\}\)
  若 \(X_1\) 和 \(X_2\) 交不为空，我们显然可以加入交集中的一个元素
  否则我们考虑换掉 I 中的一些元素，我们找到一条 \(X_1\) 到 \(X_2\) 在交换图中的最短路
  将 \(S/I\) 中的点加入，\(I\) 中的点删除（走到的点）,一次迭代过后大小显然增加 1
  结束时，不存在 \(X_1\) 到 \(X_2\) 的路径，且 \(U=\{z\}\)，z 可以到达 \(X_2\)

• 正确性证明：
  先证最后的 \(|I|=\min r_1(U)+r_2(S/U)\)，注意到我们只需证明 \(r_1(U)\le |I\cap U|\)
  假设 \(r_1(U)> |I\cap U|\)，那么存在 \(x\in U/I\)，使得 \((I\cap U)+x\in \mathcal{I}_1\)
  若 \(I+x\) 是 \(M_1\) 的独立集，那么 \(x\in X_1\)，存在路径，否则存在 \(y\in I/U\)，满足 \(I-y+x\in \mathcal{I}_1\)，这导致 \(y\in U\)（最优性）
  下面是合法性的证明：
  

• 复杂度：每一步是个 \(n\) 个点 \(rn\) 条边的图，要跑 \(r\) 次，复杂度 \(O(r^2n)\)

• 带权拟阵交：
  有扩展最大最小定理：
  
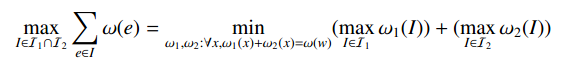
  我们将上述过程加上点权（\(S/I\)中的是正，\(I\)中的是负），跑最长路（边数小为第二关键字）就可以了