P1502 窗口的星星 题解

题目传送门。

思路

扫描线

扫描线

首先，将题目中给出的条件和问题进行转化：

首先先不考虑边框上的点不算在内的限制，考虑一个点可以对那些矩形产生贡献。

只考虑矩形的右上角，容易发现，每个星星的亮度只对右上角在以星星为左下角的长为 \(W\)，高为 \(H\)的矩形有贡献。
如图。

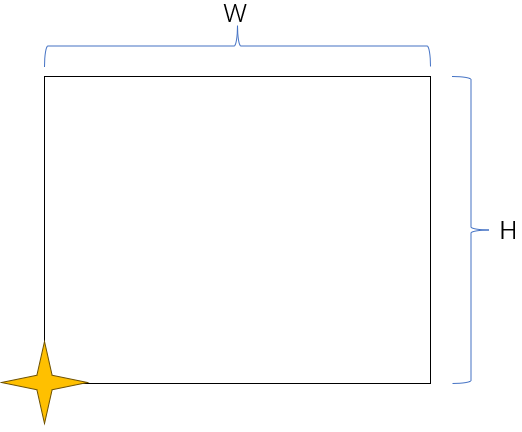
那么便可以把问题进行转化：在平面直角坐标系上有 \(n\) 个有权值矩形，求他们最大的重合的权值。

于是就可以用扫描线来解决了。

再考虑边框上的点不算在内的限制，因为可以这样框：

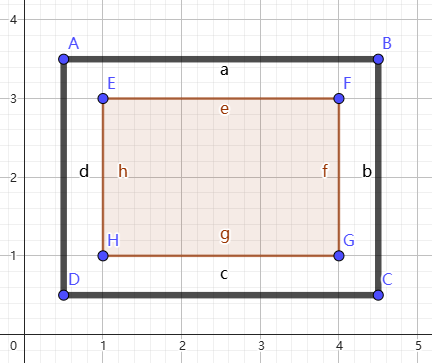
有效的矩形就相当于 \(W - 1\)，\(H - 1\) 的能取边框上的点的矩形，然后像上面那样做就可以了。

细节

对线进行排序时，要注意若两条线重合，应按权值从大到小排序。
因为可能两个矩形贴合，而又能取矩形边框上的点，所以不排序的话权值可能算小。

点击查看代码

代码

/*
  --------------------------------
  |        code by FRZ_29        |
  |          code  time          |
  |          2024/08/11          |
  |           11:02:16           |
  |             星期天            |
  --------------------------------
                                  */

#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
typedef long long LL;

using namespace std;

void RD() {}
template<typename T, typename... U> void RD(T &x, U&... arg) {
    x = 0; LL f = 1;
    char ch = getchar();
    while (ch < '0' || ch > '9') { if (ch == '-') f = -1; ch = getchar(); }
    while (ch >= '0' && ch <= '9') x = (x << 3) + (x << 1) + ch - '0', ch = getchar();
    x *= f; RD(arg...);
}

const LL N = 1e4 + 5;

#define LS (rt << 1)
#define RS (rt << 1 | 1)
#define MID (l + r >> 1)
#define LF(i, __l, __r) for (LL i = __l; i <= __r; i++)
#define RF(i, __r, __l) for (LL i = __r; i >= __l; i--)

struct tree{
    LL l, r, mx, add;
    tree(LL l = 0, LL r = 0, LL mx = 0, LL add = 0) : l(l), r(r), mx(mx), add(add) {}
} tr[N << 4];
struct seg {
    LL l, r, h, val;
    seg(LL l = 0, LL r = 0, LL h = 0, LL val = 0) : l(l), r(r), h(h), val(val) {}
} a[N << 1];
LL t, n, w, h, Y[N << 1];

void up(LL rt) { tr[rt].mx = max(tr[LS].mx, tr[RS].mx); }
bool cmp(seg a, seg b) { return (a.h != b.h ? a.h < b.h : a.val > b.val); }

void Init() {
    memset(a, 0, sizeof(a));
    memset(tr, 0, sizeof(tr));
}

void build(LL rt, LL l, LL r) {
    tr[rt] = tree(l, r, 0LL, 0LL);
    if (l == r) return;
    build(LS, l, MID), build(RS, MID + 1, r);
}

void down(LL rt) {
    tr[LS].mx += tr[rt].add;
    tr[RS].mx += tr[rt].add;
    tr[LS].add += tr[rt].add;
    tr[RS].add += tr[rt].add;
    tr[rt].add = 0;
}

void update(LL rt, LL L, LL R, LL val) {
    LL l = tr[rt].l, r = tr[rt].r;
    
    if (L <= l && r <= R) {
        tr[rt].mx += val;
        tr[rt].add += val;
        return;
    }

    down(rt);
    if (L <= MID) update(LS, L, R, val);
    if (R > MID) update(RS, L, R, val);
    up(rt);
}

int main() {
    RD(t);

    while (t--) {
        Init();
        RD(n, w, h);
        w--, h--;

        LF(i, 1, n) {
            LL x, y, l;
            RD(x, y, l);
            Y[2 * i - 1] = y, Y[2 * i] = y + h;
            a[2 * i - 1] = seg(y, y + h, x, l);
            a[2 * i] = seg(y, y + h, x + w, -l);
        }

        n <<= 1;
        sort(Y + 1, Y + n + 1);
        LL len = unique(Y + 1, Y + n + 1) - Y - 1;
        sort(a + 1, a + n + 1, cmp);

        LF(i, 1, n) {
            LL low_l = lower_bound(Y + 1, Y + len + 1, a[i].l) - Y;
            LL low_r = lower_bound(Y + 1, Y + len + 1, a[i].r) - Y;
            a[i].l = low_l, a[i].r = low_r;
        }

        build(1, 1, len);
        LL ans = 0;

        LF(i, 1, n) {
            update(1, a[i].l, a[i].r, a[i].val);
            ans = max(ans, tr[1].mx);
        }

        printf("%lld\n", ans);
    }
    return 0;
}

/* 
 * ps:FRZ弱爆了 
 * 感冒写的代码唐爆了……
 */

前尘隔海，古屋不再。