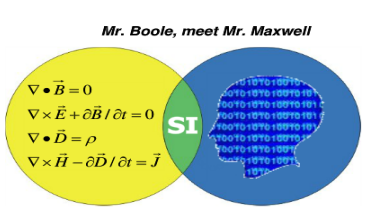
SI解释1
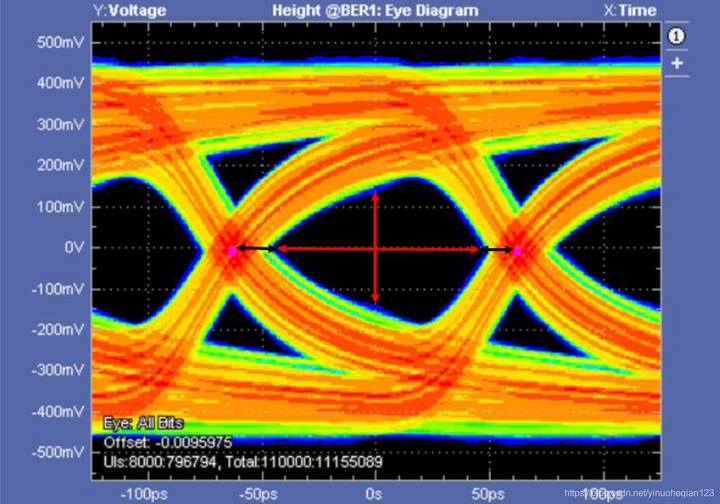
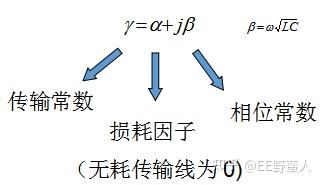
估计大多数硬件工程师在工作的头几年，都读过Eric版的《信号完整性分析》这本书。我的第一份工作也是做SI。当时从学校毕业出来也没接触过SI，能在学校里面接触SI的机会应该也非常少。后来也是开始啃这本《信号完整性分析》，然后知道了始端匹配，末端端接，传输线的特性阻抗等等。学了有一段时间之后，也总有这样那样的一些困惑。这也是学习新事物的必然规律，开始从第一个阶段，提不出什么问题，因为都是问题，然后有问题，有困惑，去找答案，再到想明白问题，最后到实践验证自己的想法，然后又发现很多新问题，呵呵。对于学习过一段时间SI的同学，不知道会不会有下面这样一个疑惑，如下图:
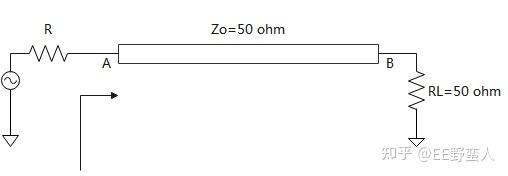
我们知道当RL等于特性阻抗Zo的时候，在负载点B的位置，反射系数是0。没有反射。就如大家都知道的反射公式计算的那样。
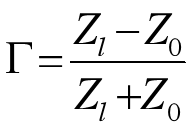
好，接下来，让我们考虑两个问题。
Q1： 我们想在A点，从上图箭头方向看过去，没有反射，条件是R=Zo嘛?
可能大部分人应该都能立刻说出答案，确实是R=Zo=50 ohm，不过这里肯定是有个“但是”滴。之前初学反射的时候，书本上很多时候都是告诉我们始端电阻（具体可能是信号源内阻+外接始端串联电阻）=传输线特性阻抗的时候，阻抗匹配，没有反射，very nice。但是那时候我就一直觉得很奇怪，感觉怎么把一个集总式的电阻去和一个有点像分布式的特性阻抗的东西去比较呢？这两个难道不是属于不同类型的东西嘛？刚开始看Eric的那本书的时候也是没有找到答案。直到后来才搞明白，这里的答案R=Zo=50 ohm是有一个前提条件的，那就是：RL=50 ohm。
Q2：当RL = x 不等于50 ohm的时候，我们的R又该怎么选才能在A点看过去没有反射呢？
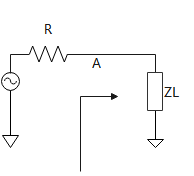
这次可能很多人都要回答不上来了，看上面这个图里面，如果把传输线和RL等效成了ZL，（我们的反射计算公式中，其实用的也都是阻抗，而不一定是电阻）是不是我们的R如果等于ZL，反射系数就等于0了。
之前当RL=50 ohm，Zo=50 ohm的时候，其实实质就是因为等效的ZL就等于50 ohm，所以才有了那个答案：R=50 ohm的时候反射系数是0。所以这个是有前提条件的。那么怎么计算ZL呢？RL变到ZL是一个传输线阻抗变换的过程。这个过程如果从史密斯圆图上去理解，就非常直观简单了。
这里引出了一些诸如阻抗变换，史密斯圆图的概念。其实是从射频电路理论里面弄出来的概念。当时学习信号完整性的时候，太注重从时域角度去理解，对一些东西理解起来其实比较难。但是从频域角度去理解就有种豁然开朗的感觉，因为数字信号的方波，可以理解为一系列的单一频点的正弦波的叠加（傅里叶级数），是一个宽带信号，而这些正弦波里面的基频正弦波尤为重要，一般是高速数字信号研究的重点对象。对于研究单一频点的正弦波（窄带信号）在频域角度是最佳的，分析思路完全按照射频理论那一套来就可以。所以其实高速SI理论其实还是以射频理论为基础的，特别是里面的传输线理论尤为重要。上面的问题就是一个最好的引子，让我们在从时域角度看SI一段时间之后，转到频域角度去审视一下它。
想从频域研究SI，免不了先要理解一下传输线。电压和电流在一对传输线上传播。就如下图，假设我们的信号就是一个单一频率的正弦波，但是频率很高，导致在这个传输线上传播过程中，线上面的各个点的电压电流都是随着位置（z）和时间（t）是波动变化的。这也就使得对于这根“线”来说我们不能等同于普通的电源线那样，接上电之后，线上的任何一点电压都几乎是一样的(不考虑压降)，并且不会随时间波动。世上本没有传输线，通过的信号频率高了，也就有了我们这里的传输线。
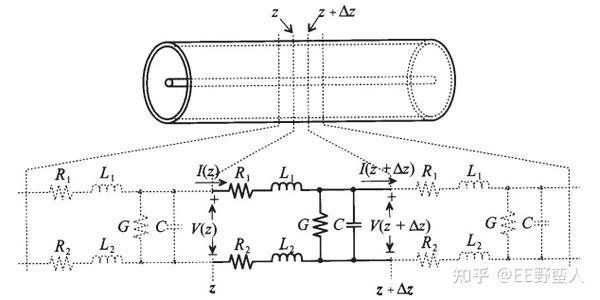
对于传输线，通常的研究方法是，对其中某一个小段进行微观的研究。用微积分的思想取其中一小段，这一小段有分布电阻，分布电感，分布电导，分布电容。
在工程上，对于高速数字信号来说，PCB上的导体损耗就是由分布电阻引起的，而介质损耗就是由于分布电导引起的。当频率高到一定程度之后，介质损耗会大于导体损耗占主导地位。电感和电容则是无耗的，但是会产生相移。上面一个单元电路的基尔霍夫定律的方程，经过一定的微分方程的复杂运算之后，就得到了下面很有名方程组，称之为电报方程：
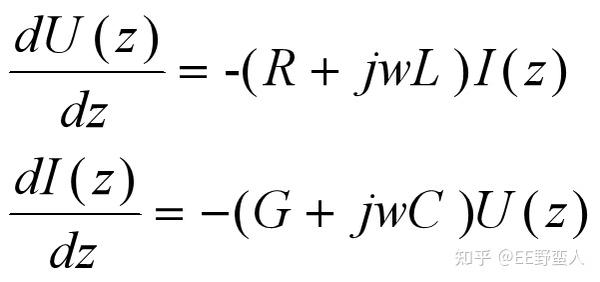
而它的解，如下所示，它揭示了在某一点的电压和电流分别由入射波和反射波两部分组成：
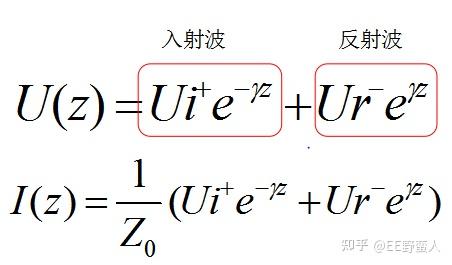
而这里的
Zo就是我们在上文提到的特性阻抗。
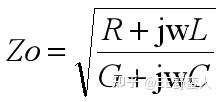
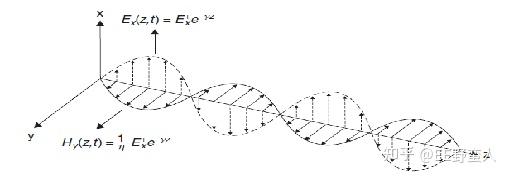
当我们把电压和电流分成入射波和反射波两部分看待的时候，可以发现特性阻抗其实就是入射电压波与入射电流波的比，或者是反射电压波与反射电流波的比。特性阻抗是对于单一方向的波而言的，对于总的电压值来说毫无意义。
当传输线为理想无耗的时候，我们的模型里的R和G就为0了，当然实际上这样的无耗是不存在的。只是在一些理想建模的情况下可以把R,G忽略。可以想想把R,G去掉，Zo就成了什么？
SI是研究信号完整性的，而这个信号，我们之前从数字方波的宽带信号，简化为研究单一频点的窄带信号，而这个单一频点的信号，又是由入射波和反射波叠加在一起组成的，哪接下来只要把信号分成入射波和反射波单独研究不就行了。再直白一点，SI研究的单一频点的波，可以近似理解为TEM波，传播方向只朝着传输线方向前进。
参考文献：
微波工程（第三版）David M. Pozar
对了，最近开通的微信公众号，可以微信搜索 “ 电子工程师那些事儿” 加关注，里面会同步更新原创类《电子工程师那些事儿》，想要了解硬件与嵌入式软件设计以及它们之前如何连结的故事，可以关注专辑。除此之外还会带一些其他的杂散类技术相关的分享，欢迎关注，评论！
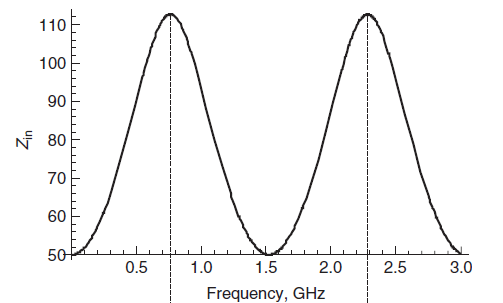
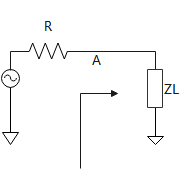
上文，我们提到了要判断真正的阻抗匹配，必须得到Zin的等效输入阻抗。就是下图这个Zin。这次我们就来聊这个问题。
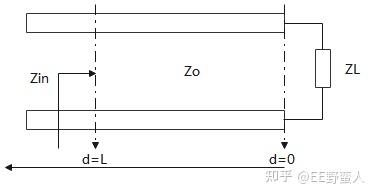
还记得上文说道传输线忽略电阻和电导的时候，是无耗传输线模型。我们研究这个Zin的时候也是需要先用无耗的模型。先看简单的，复杂的就是简单的叠加而已。并且简单的更能看清楚其中的套路。我们设d=0点的反射系数是 Γ0 ，而d=L处的反射系数是 Γ� 。
对于无耗传输线来说，之前的电压方程就简化成了下面这样。
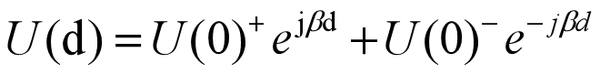
假设我们给一个初始条件，负载阻抗是ZL，当然传输线的特性阻抗是Zo：
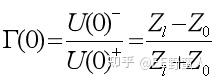
则：
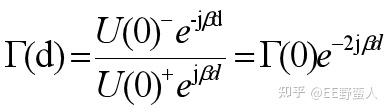
结论1：:在一段传输线，末端有负载的情况下，传输线距离d处的反射系数与负载端(d=0)的反射系数的模是一样的，并且反射系数本身是周期性的。
有了上面的这个公式，对Ud / Id做进一步的简化：
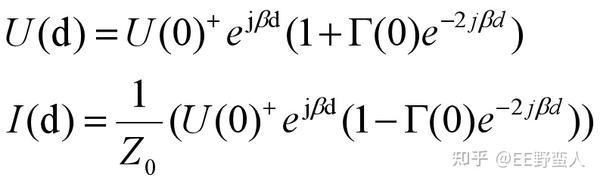
最后：
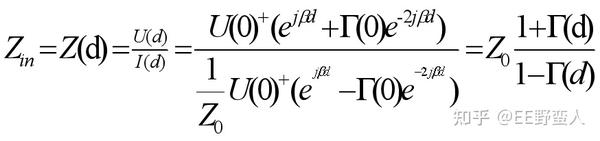
当然我们已知的是 Γ0 ，所以经过一个比较复杂的运算之后，终于得到了Zin最后的样子。
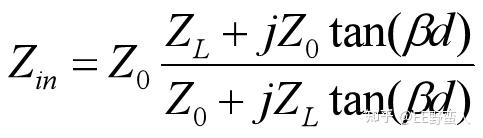
结论2：等效输入阻抗也是周期性变化的，并且周期是1/2波长。
虽然这里公式相对来说理论性比较强一点，但是估计这个是传输线理论最重要的算式了。它揭示了一个负载经过一段传输线（长度为d）之后，呈现出来的等效输入阻抗和反射系数都是周期性变化的，并且反射系数的模还不变，只是相位发生变化。这个对于我们后面理解理想回损曲线为什么是周期的，以及理解史密斯圆图上的等反射系数圆等等，极其重要。
对于Zin的结果，有几个特殊场景：
当ZL=0，ZL= ∞ ，或者d= � /4 三种情况的时候，即负载短路，负载开路，线长等于1/4波长的时候：
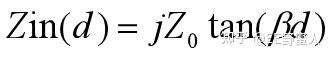
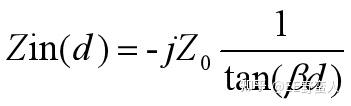
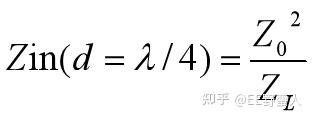
其中
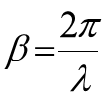
后面其实大多数情况我们在说传输线的长度的时候不常用长度d, 而是会用电长度（几分之几波长）来表示，这样更方便在频域中来理解。
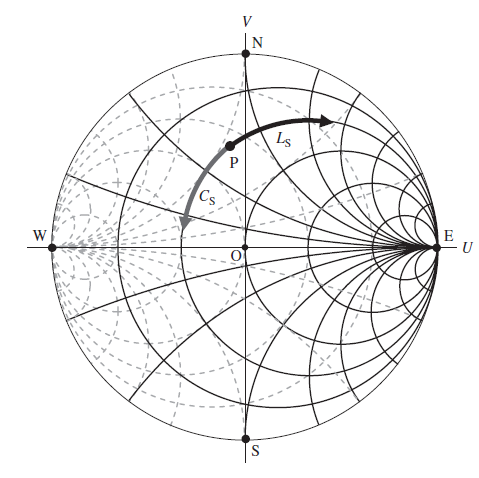
接着上篇，理解了一个负载阻抗经过一段传输线之后，能得到一个等效的阻抗。但是计算过程或者说公式却非常复杂。想起以前初中代数课的时候，数学老师讲过用图像方法解代数问题，让问题更加直观明了。史密斯圆图就是这么一个工具。把抽象的算式直接对应到一张圆图上，简洁明了。当时刚学习这个东西的时候，就感觉是个神奇的存在。记得在前面刚开始分享SI的第一篇就提到，用史密斯圆图去理解阻抗变换非常简单。其实就是一个点在圆图上转圈圈就完成了变换。
上文列出的两个重要公式结论，
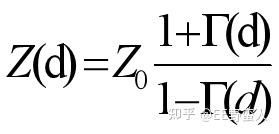
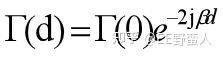
Smith圆图的核心思想是进行阻抗的归一化以及电角度的归一化：
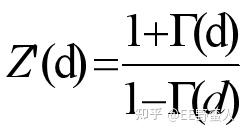
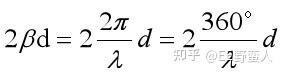
当d长度等于1/2波长的时候，正好反射系数是一个周期。在圆图上就是1/2波长传输线对应旋转360度。这里可见圆图都是跟具体的波长即频率挂钩的，所以都是研究单一频点的。
对上面算式用阻抗的实部虚部以及反射系数的实部虚部来表示的话就可以得到Smith原理图的等电阻圆以及等阻抗圆了，如下图。具体推导的话，可以参考[1]。
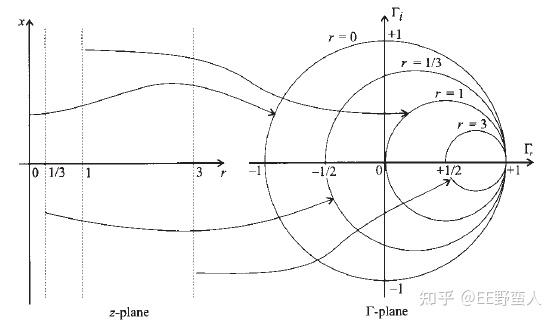
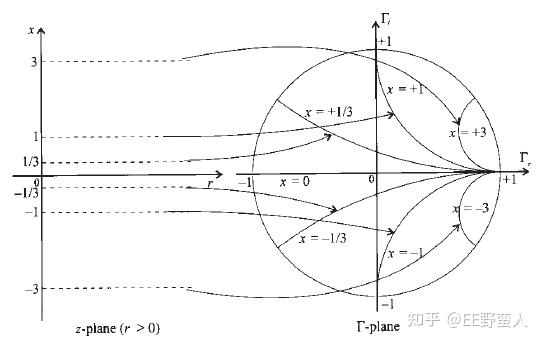
特别需要注意的地方就是：
1) 1/2的波长 表示圆图的一周。
2) 圆图的中心点表示归一化的阻抗r=1，其他所有阻抗在放到圆图之前都必须要先除以特性阻抗归一化。
3) 圆图的横轴最右边一点表示负载开路点，反射系数是1，最左边一点是负载短路点，反射系数是-1。
4) 顺时针旋转是向着源方向，逆时针旋转是向着负载方向。
有了以上的结论之后，再来看看SI第一篇的时候提的一个问题，总的等效输入阻抗的问题。
其实就是先确定负载阻抗归一化之后在圆图上的位置，然后因为由之前的公式得知，反射系数的模是一个定值。而反射系数的模就是归一化阻抗到圆点的距离。那等效阻抗就等价于负载阻抗绕着等反射系数圆顺时针旋转一个传输线长度（电角度）之后，就可以得到等效阻抗了。例如下图就是一个ZL负载在电角度为192°的传输线之后，的等效输入阻抗Zin。
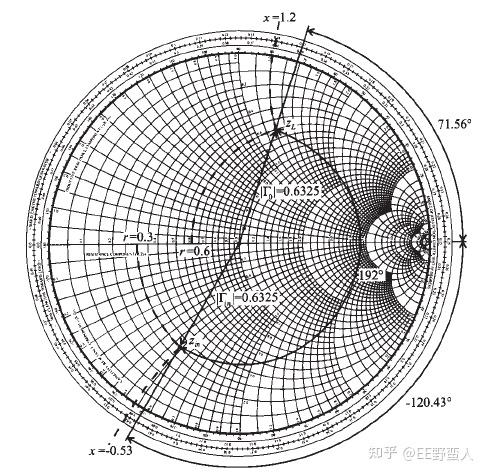
对于无耗传输线来说，我们旋转的轨迹都是在等反射系数圆上，就是一个理想的圆形轮廓，这让我们看到圆图里面解决反射系数和阻抗之间关系的问题变得简单和直观。如果传输线有耗了呢？用直觉想想，这里的旋转轨迹就不再是一个圆形，而会变成一个螺旋线了，反射系数模将会变大。如果传输线很长，负载阻抗点绕着圆图的原点旋转，最后可能就是一个半径不断在扩大的螺旋线。
关注微信公众号：电子工程师那些事儿
有更多相关内容
参考文献
1. RF circuit design Theory and Application Reinhold Ludwig
