为何50Ω占多数？同轴特性阻抗详解
在选择同轴线缆或组件时，一般我们都会看到或者要求传输线阻抗需要保持在50欧姆，有时这也会成为传输线的特性阻抗，当然75欧姆偶尔也会被用到，为何这两者会如此固定？本期我们将从这个角度出发，探讨同轴中的另一个重要参数，特性阻抗。
其实这个问题也很简单，我们快速做一个总结，可以直接看下图。
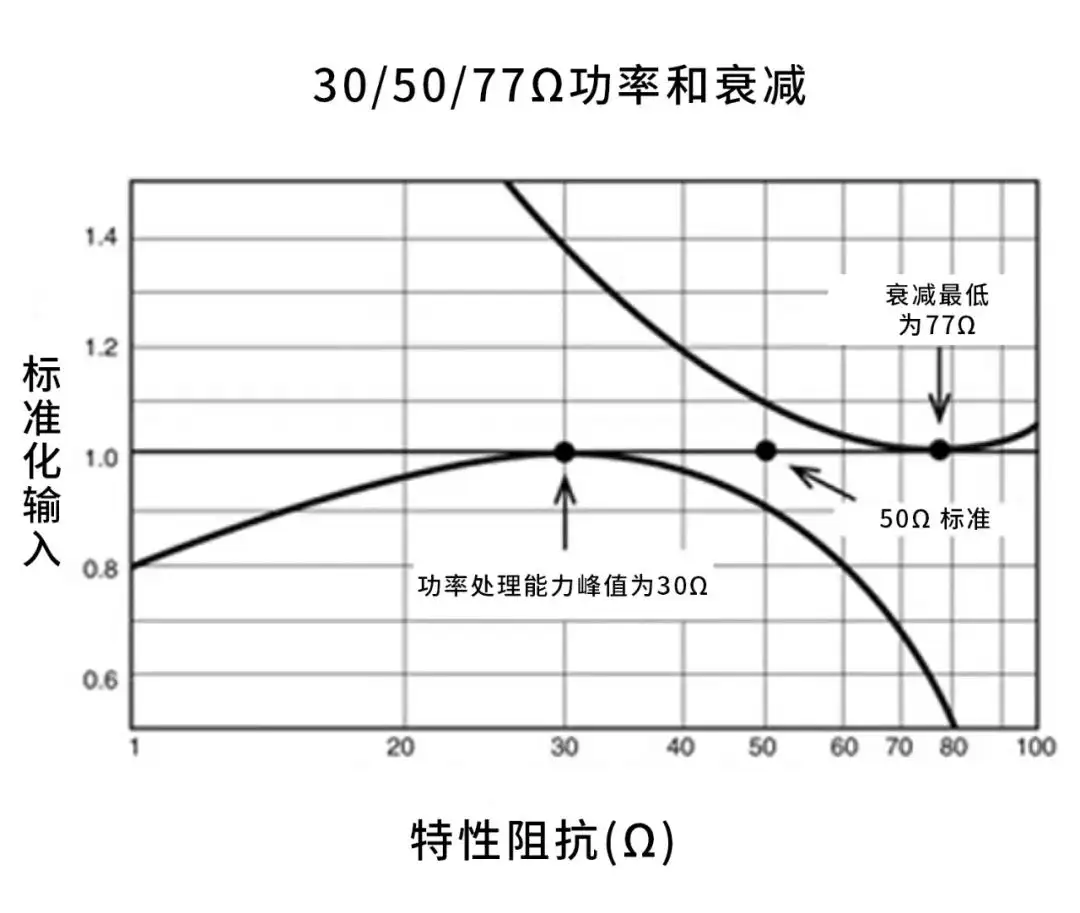
根据实验证明，插入损耗最小，约为77欧姆。另一方面，如果绘制最大功率传输与特性阻抗的关系曲线，则最大功率约为30欧姆。当下降到最大功率传输时，特性阻抗值为30欧姆，而理论上最小衰减（损耗）的特性阻抗为77.5欧姆。
在损耗和功率之间需要权衡的RF和微波，选择传输线的阻抗值为50欧姆。另一方面，当在较长的同轴线缆（如电缆或卫星电视）中要求最小的损耗时，对功率传输的优化就不再那么担心了，因此在这些系统中使用阻抗更高的75欧姆线缆和连接器。
不同的阻抗也会有不同的应用领域，一般我们会做到如下的区分，当然这也不一定是最准确的，仍然需要参考实际需求。
50Ω阻抗连接器和线缆主要用于在双向通信系统中传输数据信号，其应用领域比较广泛，包括信号测试、计算机以太网主干网、无线天线馈电线缆、GPS全球定位卫星天线馈送线缆和手机系统等
75Ω阻抗连接器和线缆主要用于传输视频信号。其中通过线缆传输电视信号是一种典型应用，此时常用F型连接器，例如家庭有线电视天线连接。另一种应用是在DVD机、VCR、安防监控等系统和设备间传输视频信号，此时通常也称为音频/视频（A/V）线缆和连接器，此时常用BNC和RCA连接器。75Ω线缆常用为实心中心导体线缆RG59B/U和绞合中心导体线缆RG59A/U。
我们以BNC连接器作为例子，辨别这两种规格的方式非常简单，如图所示：50欧姆BNC连接器的接口处带绝缘体，而75欧姆则无绝缘体。
聊过了标题提出的问题后，我们回转过来，来看看特性阻抗这个关键参数。特性阻抗是射频传输线影响无线电波电压、电流的幅值和相位变化的固有特性，等于各处的电压与电流的比值，用V/I表示。
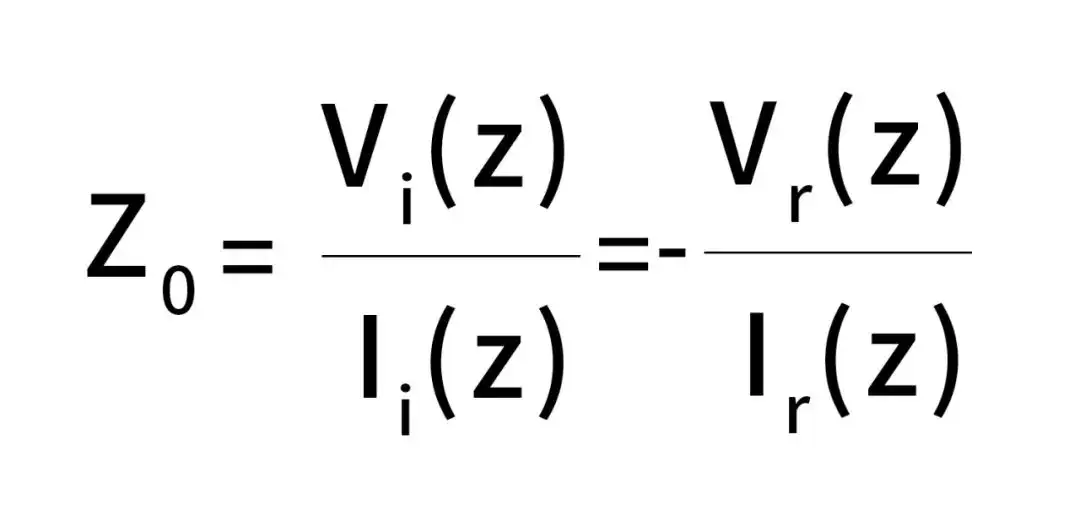
如果按照分布参数的理论去表示，传输线的特性阻抗可以表示为：
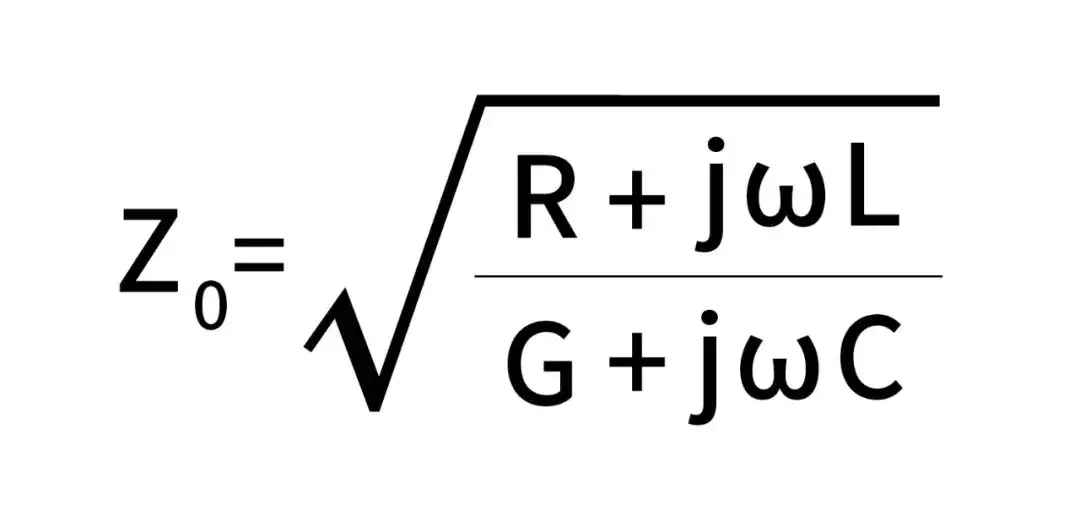
从上式可以看出，对于一个有耗传输线来说，特性阻抗是一个复数，有耗传输线的损耗就来自于这个传输线的电阻。而对于理想的无耗传输线来说，特性阻抗就是一个实数。
注意点：同轴电缆的特性阻抗和导体内、外直径大小及导体间介质的介电常数有关，而与工作频率传输线所接的射频器件以及传输线长短无关。对于一个已知特性阻抗的传输线来说，它与频率无关。
上面我们列出了阻抗50Ω和75Ω的同轴线缆的不同应用，接下来我们通过产品的形式看看它们各自应用环境下，在产品上会有什么区别。
射频工程师必知必会——为什么是“50欧姆”？
在我们的射频电路设计中，我们经常会遇到一个特殊的阻抗——50Ohm。为什么一定是50Ohm？10Ohm或者100Ohm不行吗？
带着这个问题我们一起看一下究竟？
五十欧姆阻抗的标准化可以追溯到1930年代开发用于千瓦无线电发射机的同轴电缆。A. S. Gilmour，Jr.在《Microwave Tubes》中对选择50欧姆做出了很好的解释。这个答案就是：对于空气电介质同轴电缆，50欧姆是功率容量和损耗之间的平衡。
那我们一起看一下是不是这样的吧？
为了证明这个“平衡”，我们先复习一下同轴传输线的知识。
- 同轴线是由内导体和外导体组成的双导体微波传输线。结构如下图所示：
- 同轴线主要工作模式是TEM模，主要用于宽频带馈线，设计宽频元器件；
- 当同轴线的横向尺寸和波长相比拟时，同轴线中将出现TE和TM模，是同轴线的高次模。
- 同轴线的场分布图如下：
- 同轴线的阻抗公式：
- 同轴线的功率容量：
- 同轴线的损耗：
根据上文给出的同轴线的相关公式，我们一起来计算一下到底是不是这样子的？1，假设同轴线的外导体内径为10mm，内导体外径为d从0.1mm变化到9mm，我们通过Matlab计算看一下他的功率容量和损耗都是怎么个变化吧。为了简便，我们把公式中的常数设为1。代码如下：D=10; %同轴线外导体内径为10mm
d=0.1:0.1:9;%同轴线内径为变量从0.1mm递增到9mm
%循环计算得到阻抗不同内径的阻抗值和功率容量和损耗值
for i=1:max(size(d))
P(i)=(d(i)*d(i))/120*log(D/d(i));
Z(i)=60*log(D./d(i));
Loss(i)=10/(120*3.14*D)*(1+D./d(i))/log(D./d(i));
end
[a,b]=min(Loss); %取得损耗最小值和坐标
[c,d]=max(P);%取得功率容量最大值和坐标
plot(Z,P,Z,Loss)%画图
hold on
plot(Z(b),a,'o');
text(Z(b),a+0.01,['Z=',num2str(Z(b)) ',' ,'Lmin=',num2str(a)]);
hold on
plot(Z(d),c,'<');
text(Z(d),c+0.001,['Z=',num2str(Z(d)) ',' ,'Lmin=',num2str(c)]);
hold off
运行得到：
上图中蓝色线为空气填充同轴线功率容量与阻抗的关系曲线，我们可以看到，当阻抗Z=29.6578Ohm时，功率容量最大。当阻抗Z=76.3779Ohm时，同轴线的损耗最小。那么为了得到一个较理想的功率容量，又使得损耗可以接受，我们取这两个特殊阻抗的中间为标准值Z0=（29.6578+76.3779）/2= 53.0178 Ohm。简便起见，取Z0=50Ohm
到此，我们证明了50OHm既不是一个最好的阻抗，也不是一个最差的阻抗，它只是在射频应用中的一个大家都可接受的折中方案。
那么在有些设计中上面两个阻抗极点也是极其重要的。比如在同轴滤波器设计中，我们希望同轴谐振器的损耗最低，那就需要用到 Z=76.3779Ohm这个阻抗了。这时候的同轴线内外半径比为：D/d=3.5714时，谐振腔的损耗最低。
当然如果功率容量时设计瓶颈的化，我们也会用到Z=29.6578Ohm这个特殊阻抗。这个时候同轴线的外径内径比为：D/d=1.6129.
结语：工程设计本身就是一个平衡的过程，我们平衡性能，工艺，成本。我们根据系统的需要去做有效的平衡。这本身就贯穿射频工程设计的各个阶段。
《
