高通、低通、带通 三种滤波器的工作原理
滤波器作为一种选频装置，是信号处理中的一个重要概念。目前主要由低通滤波器、高通滤波器和带通滤波器和带阻滤波器四种，当然也可以按照电路工作原理分为无源和有源滤波器两大类。
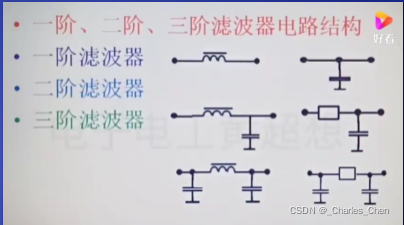
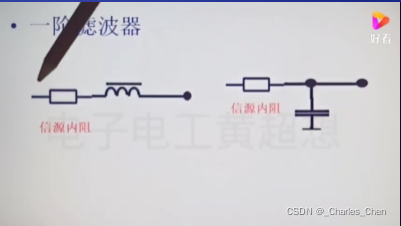
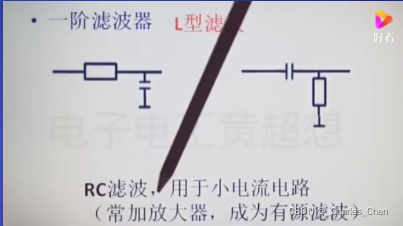
按照电容电感数量和滤波次数分：一阶、二阶、三阶滤波等。是按照多少个储能器件即滤波次数有关；两个电容并联或者串联算是一阶；
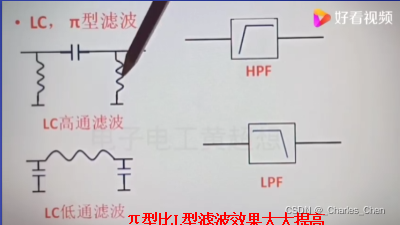
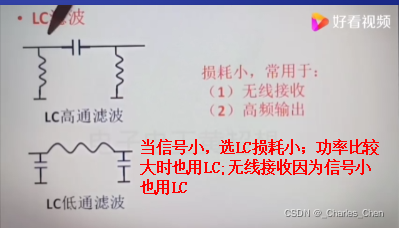
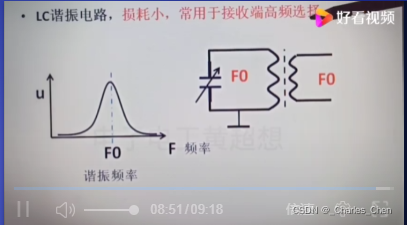
高通低通：用RLC器件构成；LC比RC损耗小，滤波效果更好。
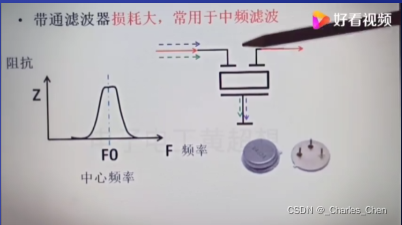
带通：有RC,LC,还有专用带通滤波器通常用专用带通滤波器：三端和五端滤波器。
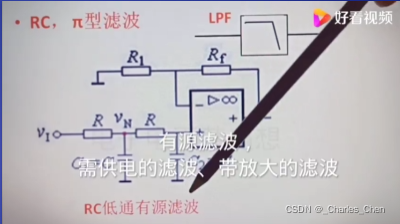
仅仅RC LC滤波的叫无源滤波
RC LC加上放大器的叫有源滤波
L 型、π型、T型
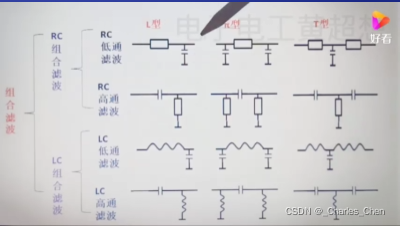
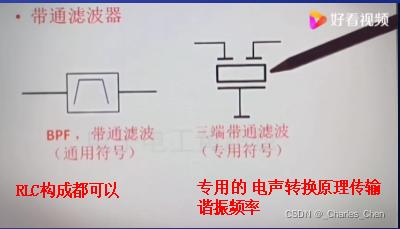
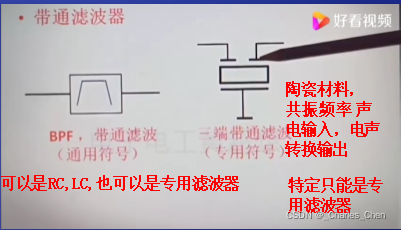
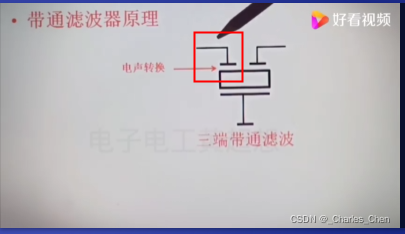
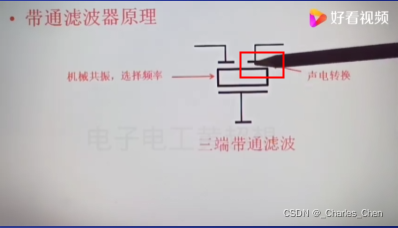
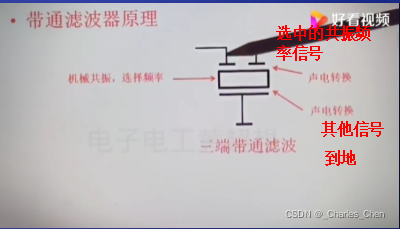
低频和高频没有被选择输出，只有合适的频率谐振频率F0才会被选择输出最强的信号，输出顶端是一个平滑的曲线 。
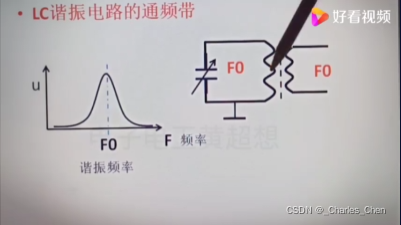
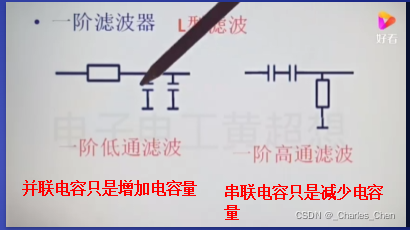
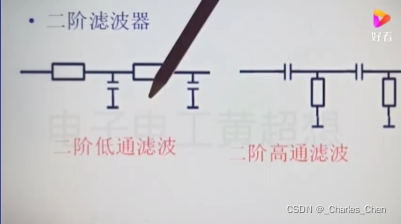
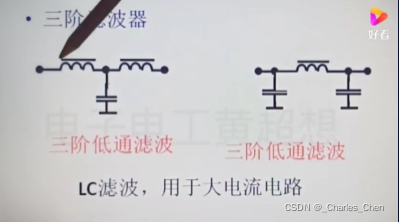
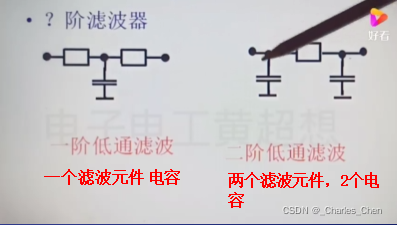
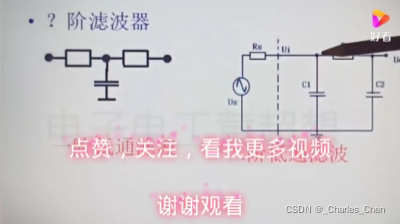
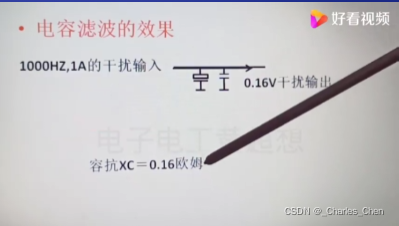
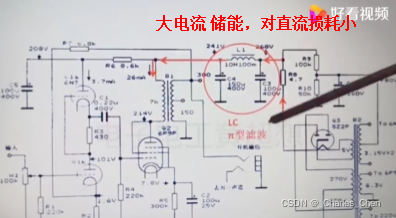
π型滤波效果（1000uf胆电容分解为两个500uf电容π滤波）
干扰输出仅为原来的0.016V，为原来的1/10
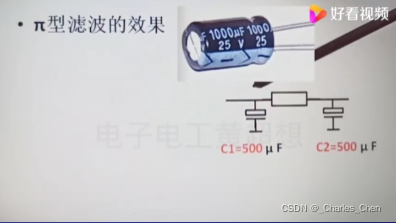
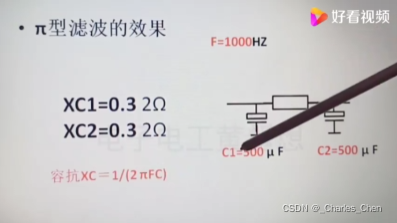
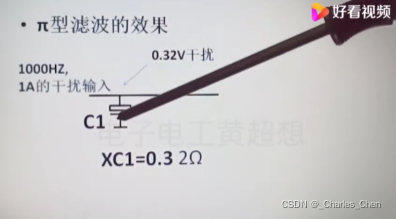
π滤波，减少纹波，提高滤波效果；R选择：几Ω到几十Ω之间；
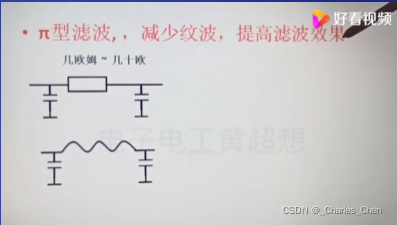
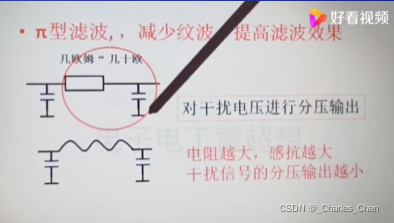
以下是低通、高通、带通滤波器的原理详述。
一、低通滤波器
【定义】
电感阻止高频信号通过而允许低频信号通过，电容的特性却相反。信号能够通过电感的滤波器、或者通过电容连接到地的滤波器对于低频信号的衰减要比高频信号小，称为低通滤波器。
负载是电阻，电感的感抗，电容的容抗三种复合物，统称为阻抗；即以下公式：
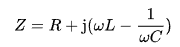其中R为电阻，wL为感抗，wC为容抗，j为虚数单位；如果括号中>0，为感性负载；如果括号中<0，称为容性负载；
【原理】
利用电容通高频阻低频、电感通低频阻高频的原理。对于需要截止的高频，利用电容吸收电感、阻碍的方法不使它通过；对于需要放行的低频，利用电容高阻、电感低阻的特点让它通过。最简单的低通滤波器由电阻和电容元件构成，如下图。
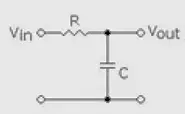
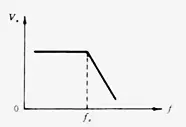
该低通滤波器的作用是让低于转折频率f。的低频段信号通过， 而将高于转折频率f。的信号去掉。
当输入信号Vin中频率低于转折频率f。的信号加到电路中时，由于C的容抗很大而无分流作用，所以这一低频信号经R输出。当Vin中频率高于转折频率f。时，因C的容抗已很小，故通过R的高频信号由C分流到地而无输出，达到低通的目的。这一RC低通滤波器的转折频率f。
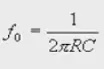
上图是主要涉及到的公式。
低通滤波器的原理解释完之后，再看下面的积分电路：
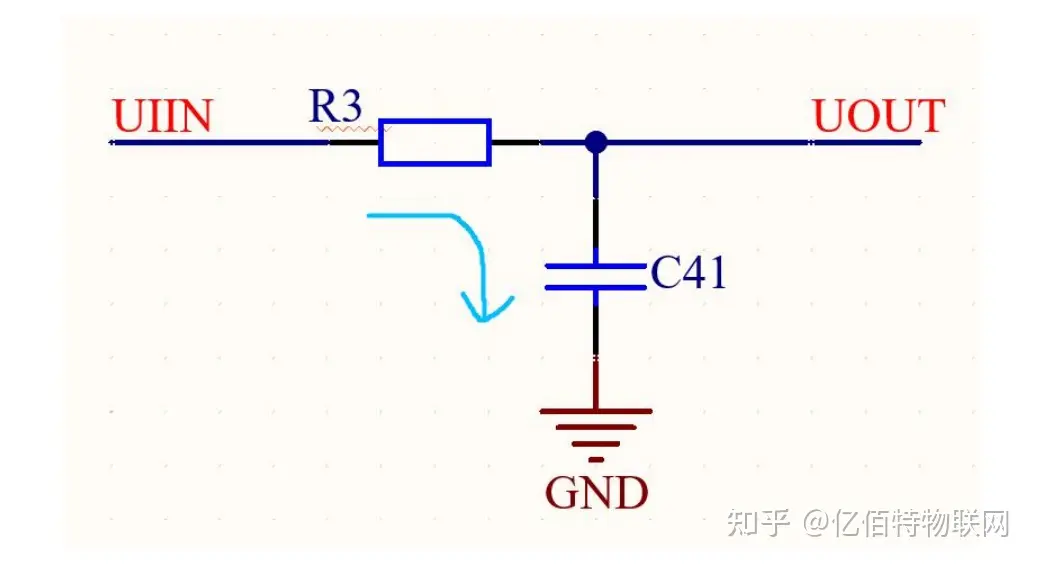
上图是简化电路之后的一个无源积分电路，简单分析这个积分电路，假设要求它的时间常数 T 需要大于它的信号脉冲宽度，而由于 T=RC，所以这个电路工作原理就是：
假设输入信号为矩形脉冲波（也可以是正弦波），当第一个脉冲波出现时，输入端产生一个电流，通过对 R3 和 C41 进行充电（电容两端的电压是不会突变的），这个时候，电容 C41 上的电压慢慢增加，当脉冲过去之后，输入端的信号 UIN 就会为 0（电容两端电压不会突变），所以时间常数 T 会比较大，相对地，它的放电就会变得很缓慢。
慢慢地，第二个脉冲又过来了，在这时，由于之前的电还是没有放掉，就可以知道，当输入脉冲波越密集，我们的 UOUT 就会越大。
总结一下来说，所谓的积分电路就是获取输入信号 UIN 的平均值形成的电路，换句话说也可以是低通滤波器电路。总结原理就是对低频段的信号进行采集采样，通过后面的电容存储，最后进行获取输入电流的平均值。下图可以形象描述：
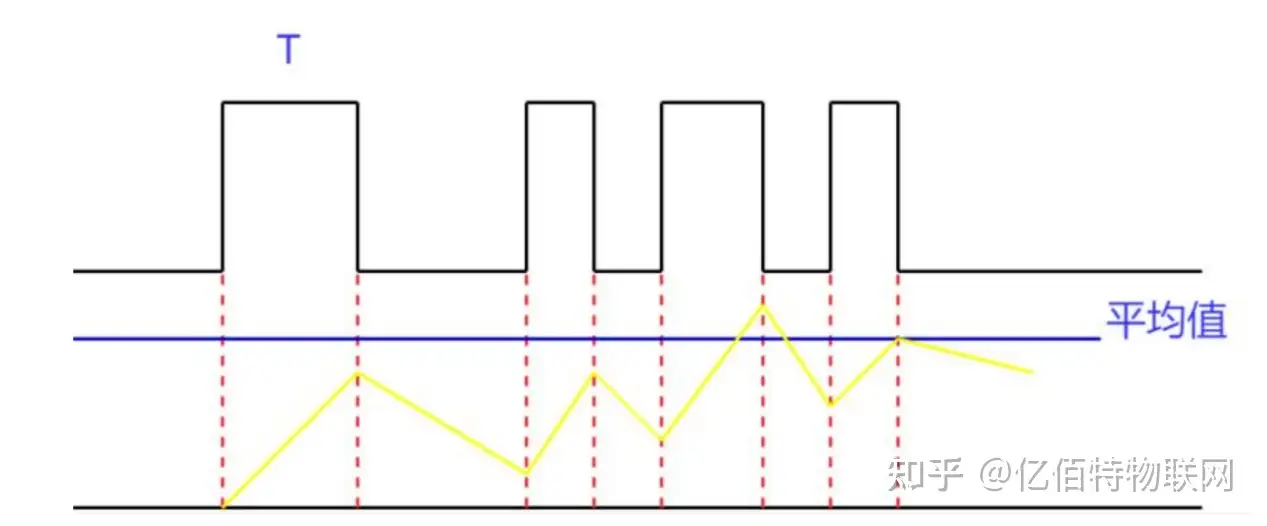
在弄清楚积分电路之后，再看低频滤波器电路就会一目了然，下面是小编绘制的两个低频滤波器电路：一阶低通滤波器、二阶低通滤波器。
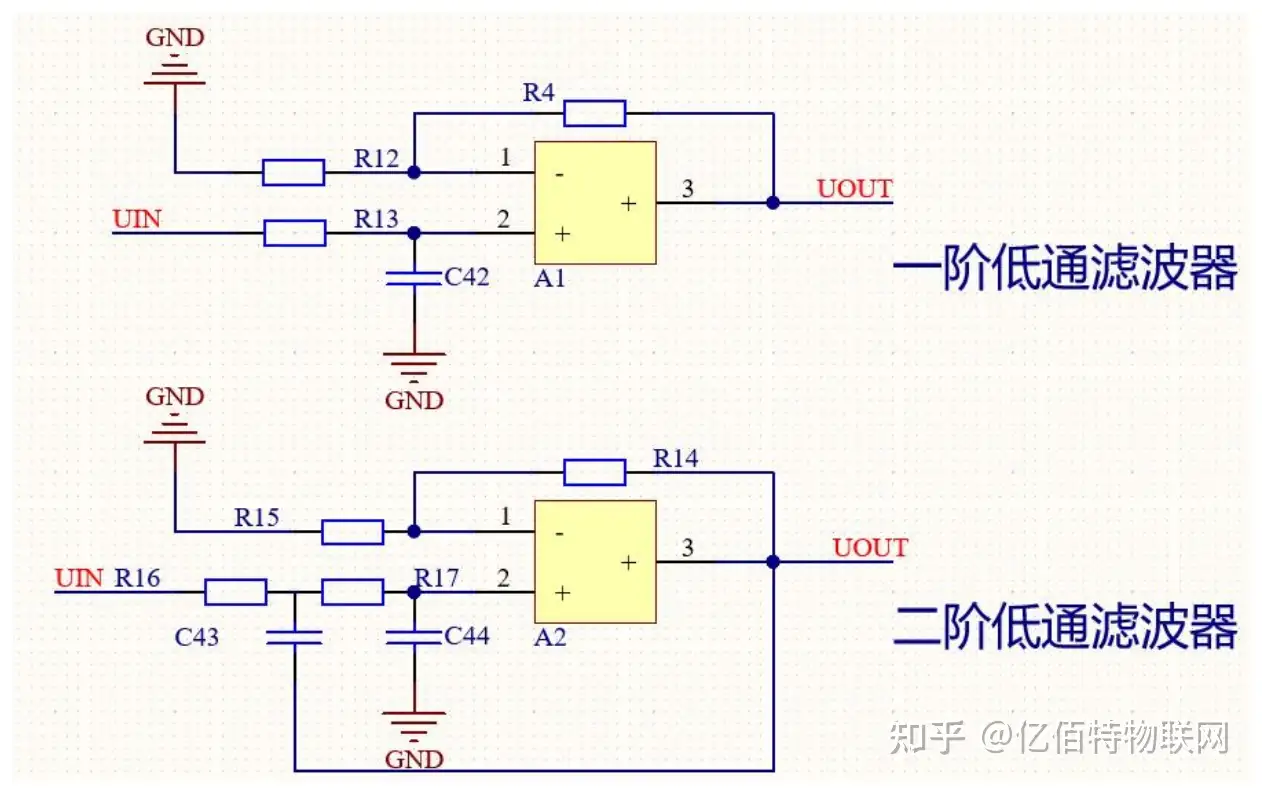
从图中，我们可以看到，两个滤波器都是由集成运放和无源低通滤波器组成（积分电路），而滤波器中反馈则是为了使运放工作在线性区域里面。分析这个一阶低通滤波器电路：
同比例运算电路（电压并联负反馈）由公式 AuP=（R4/R12）+1 计算放大倍数。
W=2πf=2π/t 计算角频率。
电阻和电容属于串联谐振，串联谐振频率就为：f0=1/（2πR13C42）。由于 PC 串联是只能用在交流回路上面进行分析的，而 RC 并联就可以用在交流和直流上。
平时电路设计中，常用的滤波器都是二阶和多阶，通过很多次的验证，都表明对于一阶滤波电路的滤波效果远远不如二阶滤波器电路效果，可以观察上面二阶滤波器原理图，有颗 C47 电容，它的作用是充当了一个正反馈的形式来改善截至频率附近的幅频效果。
二、高通滤波器
【定义】
最简单的高通滤波器是“一阶高通滤波器”，它的的特性一般用一阶线性微分方程表示，它的左边与一阶低通滤波器完全相同，仅右边是激励源的导数而不是激励源本身。当较低的频率通过该系统时，没有或几乎没有什么输出，而当较高的频率通过该系统时，将会受到较小的衰减。
实际上，对于极高的频率而言，电容器相当于“短路”一样（容抗很小，xC=1/2πfc），这些频率，基本上都可以在电阻两端获得输出。换言之，这个系统适宜于通过高频率而对低频率有较大的阻碍作用，是一个最简单的“高通滤波器”，如下图。
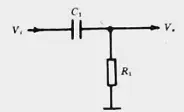
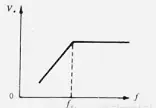
RC高通滤波器的幅频特性曲线
【工作原理】
当频率低于f。的信号输入这一滤波器时，由于C1的容抗很大而受到阻止，输出减小，且频率愈低输出愈小。当频率高于f。的信号输入这一滤波器时，由于C1容抗已很小，故对信号无衰减作用，这样该滤波器具有让高频信号通过，阻止低频信号的作用。这一电路的转折频率f。
上图是主要涉及到的公式。
同之前分析低通滤波器一样，如图分析上面的微分电路，学习电路知识的我们知道，于积分电路而言，时间常数 T 是大于输入信号的脉冲宽度的；反之，对于微分电路，时间常数 T是远远小于输入信号宽度的。
从电路分析，当一个输入信号冲出瞬间，由于电容两端电压不能突变，此时就可以把电容看成一个短路，流过的脉冲全部留到了电阻上，电阻的电压也就变得最大，但是对于微分电路来说，因为时间常数远小于输入信号的脉冲宽度，所以很快电容就开始充电，由于电容两端的电压不能马上突变，所以电容还在充电，这时候电容充电满了，充满之后，电容就成了开路状态（同时 Uout 也是 0），也就是断开了输入，这时输入脉冲就会断开消失，而变成开路的结果就是没有电流流过电阻，电阻上面就没有电压，就是相当于输入端接地。
观察电压的输入极性，左边是正右边是负，那么这个时候电阻上的电压还是最大，只不过变成了最大的负电压。这个时候开始放电，放电的同时电容两端的电压不能突变，那么这个时候，电阻上的电压还是最大，然后快速放电（由于时间 T 很小），放完之后，等待下一次的脉冲过来，此时 Uout 还是 0。
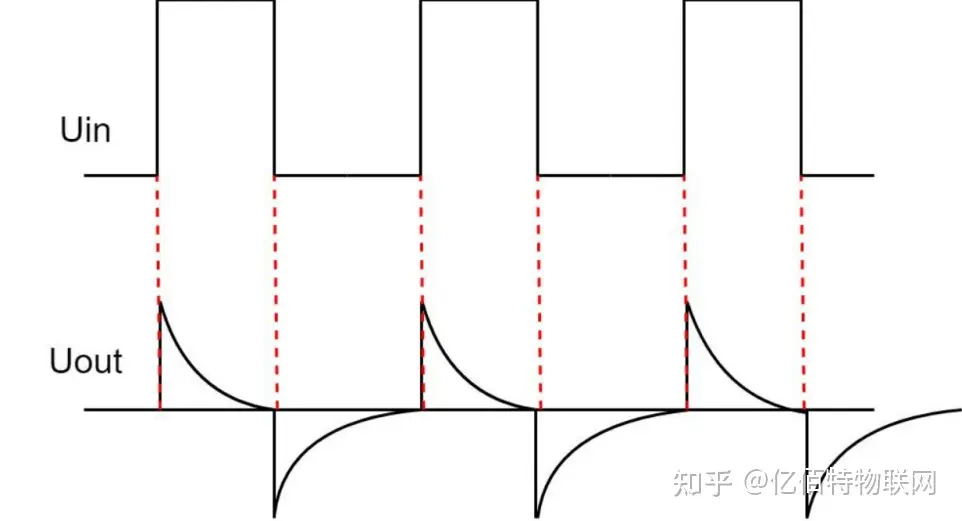
简单总结一下：微分电路其实就是通过电容不能突变的特性，让脉冲不断产生尖波，从而求出输入信号的突变成分，也就是通过改变电容和电阻阻值，来获得某一频率范围下的信号，通过一系列的尖波突变，可以知道 Uin 输入的大小不变，所以结论就是：微分电路无输出。
同样，在弄清楚微分电路之后，再看高频滤波器电路就会一目了然，下面是小编绘制的两个高通滤波器电路：一阶高通滤波器和二阶高通滤波器。
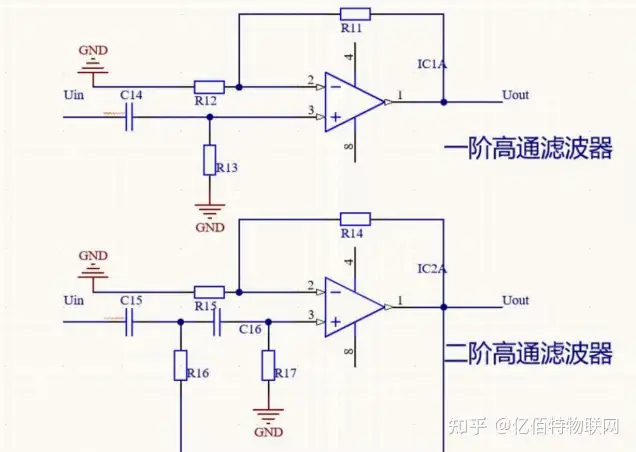
Aup=1+（R11/R12），F0=1/(2πR6C3)，二阶也是对于增加性而增加的正反馈引入。
三、带通滤波器
【定义】
带通滤波器是一种仅允许特定频率通过，同时对其余频率的信号进行有效抑制的电路。由于它对信号具有选择性，故而被广泛地应用现在电子设计中。
比如RLC振荡回路就是一个模拟带通滤波器。带通滤波器是指能通过某一频率范围内的频率分量、但将其他范围的频率分量衰减到极低水平的滤波器，与带阻滤波器的概念相对。
【工作原理】
需要注意的是，在使用过程中，滤波器并不能够将期望频率范围外的所有频率完全衰减掉，尤其是在所要的通带外还有一个被衰减但是没有被隔离的范围。这通常称为滤波器的滚降现象，并且使用每十倍频的衰减幅度的dB数来表示。
通常，滤波器的设计尽量保证滚降范围越窄越好，这样滤波器的性能就与设计更加接近。然而，随着滚降范围越来越小，通带就变得不再平坦，开始出现“波纹”。这种现象在通带的边缘处尤其明显，这种效应称为吉布斯现象。
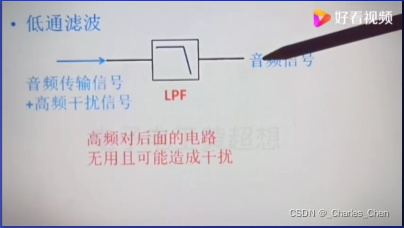
低通滤波低通滤波（low-pass filtering）：是一种滤波方式，规定为低于设定临界值频率的信号能正常通过，而高于设定临界值频率（fc）的信号则被阻隔和衰减（图1）。低通滤波可以简单的认为：设定一个频率点，当信号频率高于这个频率时不能通过。
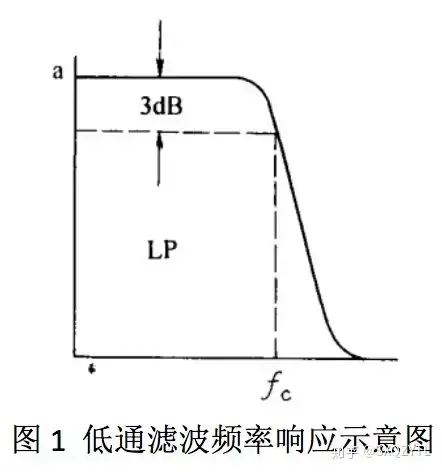
低通滤波器（low-pass filter）：只允许某一频率以下的信号无衰减地通过滤波器，其分界处的频率称为截止频率。
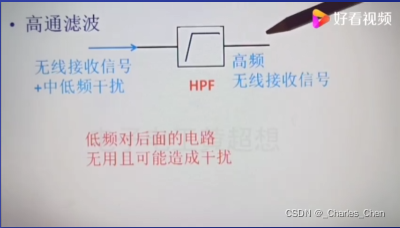
注：截止频率（cut-off frequency）在电子滤波器当中是指当保持输入信号的幅度不变，改变频率使输出信号降至最大值的0.707倍，用频响特性来表述即为输出信号降低3dB点处所对应的频率即为截止频率。它是用来说明频率特性指标的一个特殊频率，简单点说是指滤波器的输出频响幅值降低3dB时所对应的频率点。高通滤波高通滤波(High-pass filtering)：规定为高于设定临界值频率（fc）的信号能正常通过，而低于设定临界值频率(fc)的信号则被阻隔和衰减（图2）。换句话说就是只对低于某一给定频率（前述的“临界值频率”）以下的频率成分有衰减作用，而允许这个截止频率以上的频率成分通过。但是阻隔和衰减的幅度则会依据不同设定临界值频率（fc）以及不同的滤波程序（目的）而改变。
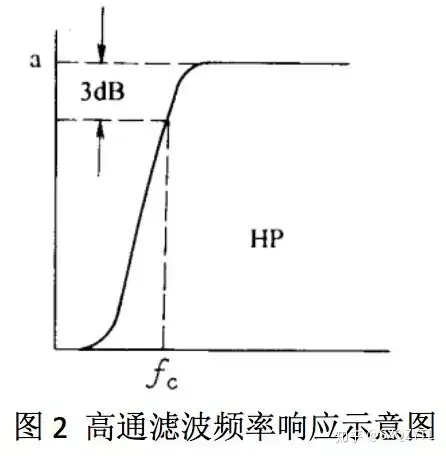
高通滤波器（High-pass filter）：只允许某一频率以上的信号无衰减地通过滤波器，去掉了信号中低于该频率的不必要的成分或者说去掉了低于该频率的干扰信号。
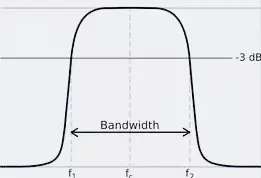
带通滤波带通滤波（band-pass filtering）：允许特定频率信号通过的滤波器，降低或消除该频带上下频率的信号（图3）。
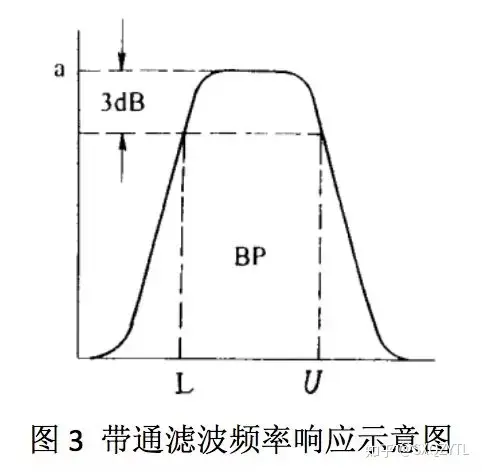
带通滤波器（band-pass filter）：可以看做是由高通和低通滤波器协同作用的结果，高通和低通滤波器的截止频率可作为通带的下限频率和上限频率（图3中的L和U点）。其主要参数是中心频率和带宽，上限频率和下限频率之差就是滤波器的带宽。
在分析噪声的频谱特征或主要频率成分时，常以一组相互衔接的带通滤波器将整个音频范围划分成若干个通带。通带的划分可以采用等带宽、等百分比、等比划分等几种形式。
带阻滤波器带阻滤波器（bandstop filters，简称BSF）：指能通过大多数频率分量、但将某些范围的频率分量衰减到极低水平的滤波器，与带通滤波器的概念相对。其中陷波滤波器（notch filter）是一种特殊的带阻滤波器，它的阻带范围极小。
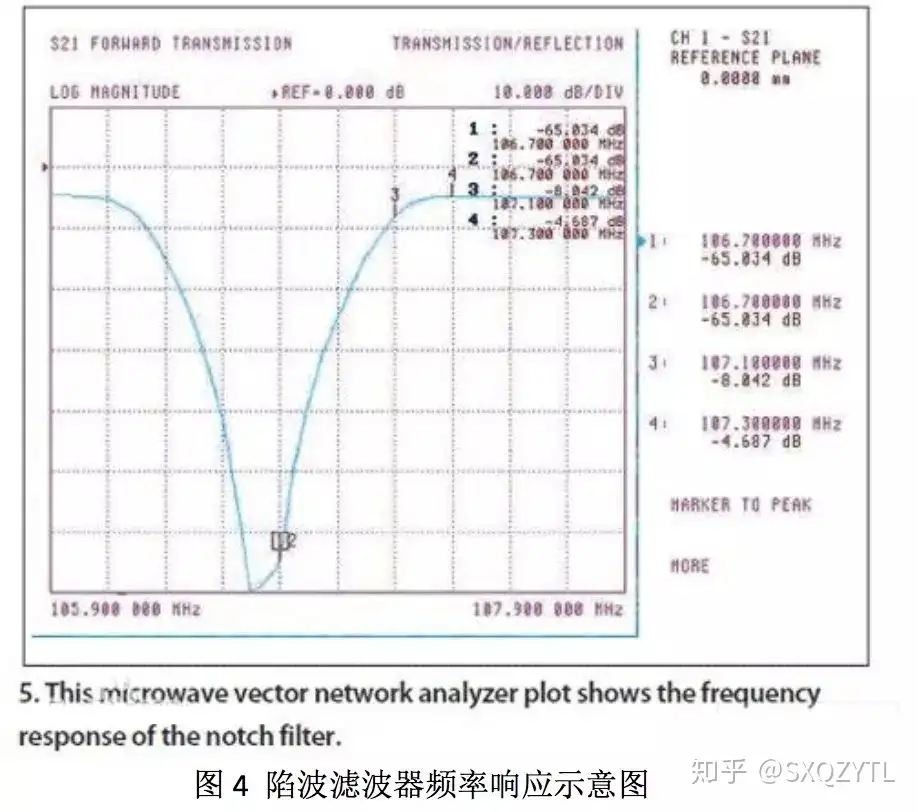
陷波滤波器陷波滤波器（notch filter）：是一种谐振电路，用在电路上滤除不需要的频率的信号，其谐振的频率就是要滤除的频率。该滤波器可以在某一个频率点迅速衰减输入信号，以达到阻碍此频率信号通过的滤波效果。一个理想的陷波滤波器的频率响应特点是：要在消除的信号频率点其值等于零，而在其他频率处其值不为零且要等于1。
听力学 应用
在听觉诱发反应中，电极记录到的反应在经过放大器之前，为了去除一些无关的电活动，需要采用一些滤波技术，以及经过放大后还需要进一步去除一些无关的电活动而采用滤波技术，该功能就是通过不同的滤波器组合来实现。例如，已知短声诱发的听性脑干反应（ABR）的主要成分在100Hz-3000Hz的范围，则可通过滤波去除小于100Hz和大于3000Hz的电活动，这样就可以保留ABR成分，获得更清晰的ABR波形，有利于临床ABR波形判别以及获得更好的反应阈值。此外，还要通过陷波滤波器消除日常公用交流电的干扰。
临床听力学中，在诱发电位测试中常用陷波滤波器用以去除50Hz的公用交流电的干扰（在欧美是用于去除60Hz的公用交流电）。对于不同的诱发电位的记录，会采用不同的高通和低通截止频率来实现信号的最有效记录。
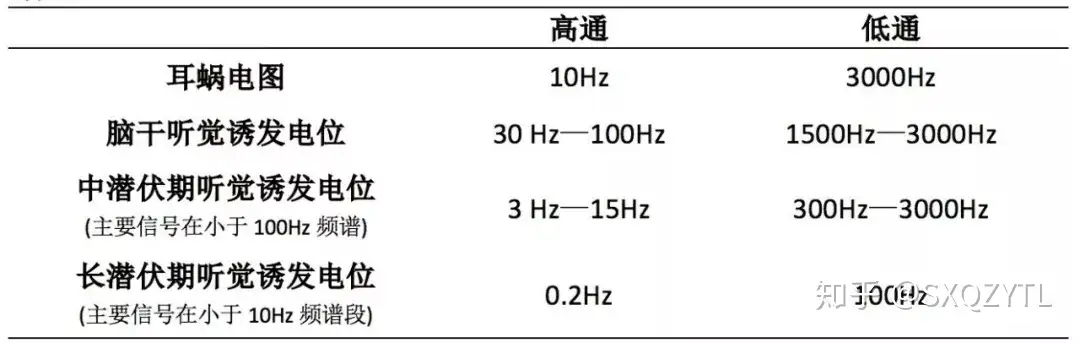
以下是临床上常见的一些诱发电位测试中常规带通滤波设置：
参考文献：
1奥本海默．信号与系统：西安交通大学出版社，2010年
2童诗白, 华成英．模拟电子技术基础（第四版）：高等教育出版社，2006
