03串行FIR滤波器

01实战原理

FIR在实现上的本质是带抽头延迟的加法器和乘法器的组合，每一个乘法器对应一个系数。只有当FIR的h(n)对称时，FIR滤波器才具有线性相位特性。使用matlab工具设计FIR时，得到的h(n)也都是具有对称性的。实现FIR滤波器的过程其实就是实现卷积的过程，卷积公式如下：

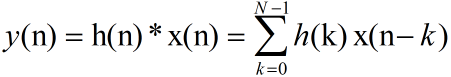
首先无论是matlab还是fpga都要得到滤波器系数，这里方法如下：

1、把matlab定义到自己路径下，并回车“fdatool”。

 

 2、设置如下参数：采样频率10KHz、截止频率3KHz

 

 3、导出FIR滤波器系数：File--Export

 

 

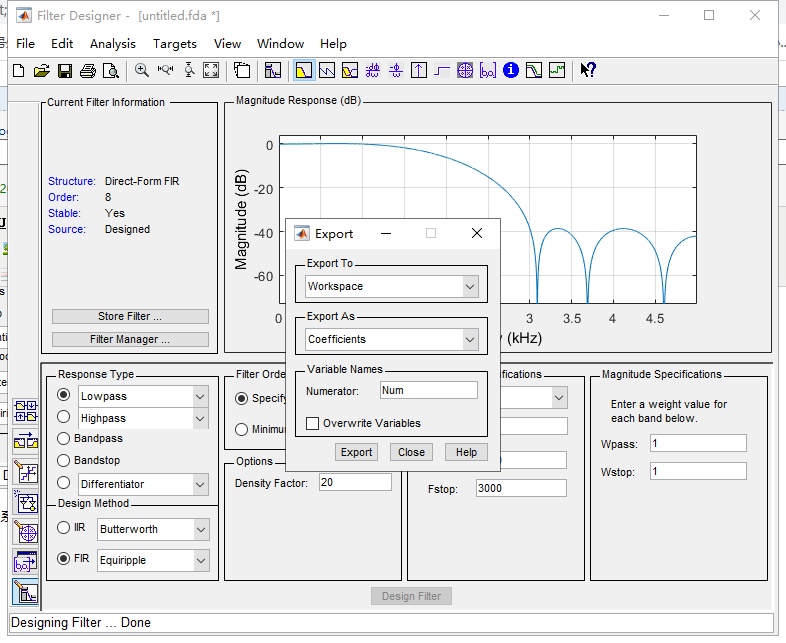
 4、将导出的8点滤波器系数放大256倍，以便于在fpga中使用

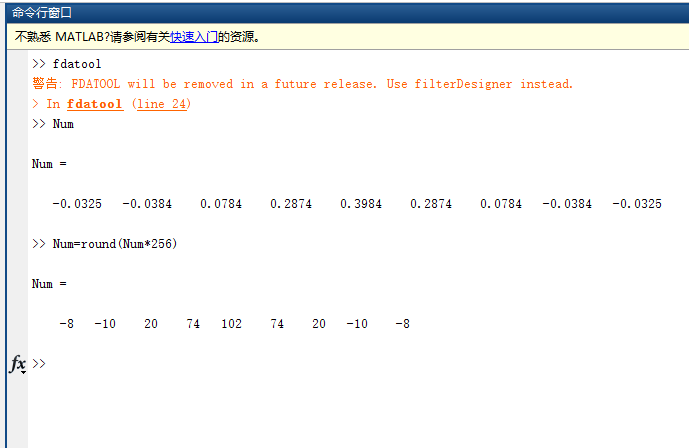
02matlab实现

使用matlab生成一个1khz+3khz+4khz的混合频率信号，并写入文本中

Fs = 10000; %采样频率决定了两个正弦波点之间的间隔
N = 4096; %采样点数
N1 = 0 : 1/Fs :N/Fs-1/Fs;
in =round((sin(1000*2*pi*N1) + sin(3000*2*pi*N1) + sin(4000*2*pi*N1))*20);
coeff =[-8,-10,20,74,102,74,20,-10,-8];
out =conv(in,coeff);%卷积滤波
%==========================================
fidc = fopen('G:\test\serial_fir\doc\out.txt','wt');  %将结果写入out.txt文件，便于和modesim数据对比
for x = 1 :4104   
    %fprintf(fidc,'%s\n',num2str(out(x))/256);
    fprintf(fidc,'%d\n',(out(x)));
end
fclose(fidc);  

subplot(2,1,1);
plot(in);
xlabel('滤波前');
axis([0 200 -150 150]);

subplot(2,1,2);
plot(out);
xlabel('滤波后');
axis([100 200 -5000 5000]);

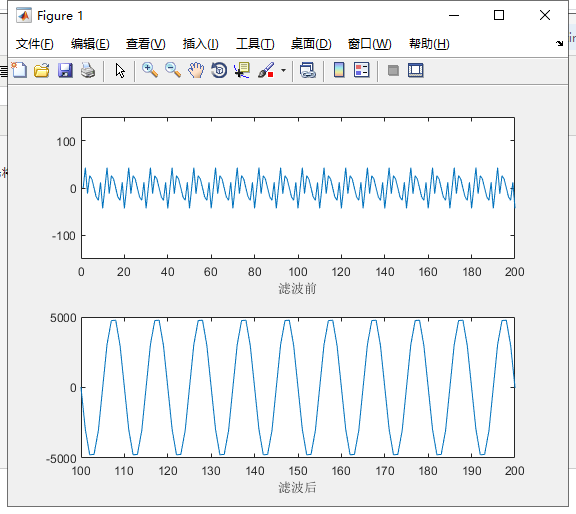
03fpga实现

设计8阶滤波器，那么长度为9。

matlab产生1khz+3khz+4khz三个正弦波叠加波形，用于激励文件的仿真输入波形

Fs = 10000; %采样频率决定了两个正弦波点之间的间隔
N = 4096; %采样点数
N1 = 0 : 1/Fs : N/Fs-1/Fs;
s = sin(1000*2*pi*N1) + sin(3000*2*pi*N1) +sin(4000*2*pi*N1);%三种正弦波
fidc = fopen('G:\test\serial_fir\sim\mem.txt','wb');  %将结果写入mem.txt文件，便于modesim使用

for x = 1 : N
    A = round(s(x)*20);
   if (A >= 0)
      bin_x = dec2bin(A, 8);        % 正数的反码和补码都和原码一样
      fprintf(fidc,'%s\n',bin_x);
   else
      bin_x = dec2bin(2^8 + A, 8);
      fprintf(fidc,'%s\n',bin_x);
   end
end 

fclose(fidc);  

04fpga仿真