02 串行FIR滤波器(利用IP核)
01实战原理
滤波器是一种用来渐少或消除干扰的电气部件,其功能是对输入信号进行过滤处理得到所需的信号。滤波器最常见的用法是对特定频率的频点或该频点以来的频率信号进行有效滤除,从而实现消除干扰、获取某特定频率信号的功能。这里设计的滤波器是低通滤波器:容许低于截止频率的信号通过而高于截止频率的信号则不能通过。数字滤波器可分成无限脉冲响应(Infinite Impulse Response,IIR)滤波器和有限脉冲响应(Finite Impulse Response,FIR)滤波器,二者的根本区别在于系统函数结构不同。
FIR:
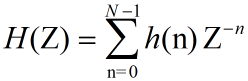
IIR:
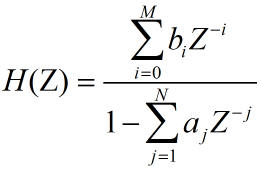
FIR滤波器,即有限脉冲响应滤波器,顾名思义,是指单位脉冲响应的长度是有限的滤波器。具体来讲,FIR滤波器的突出特点是其单位取样响应h(n)是一个N点长的有限长序列,0 ≤ n ≤ N-1。滤波器的输出y(n)可表示为输入序列x(n)与单位取样响应h(n)的线性卷积。
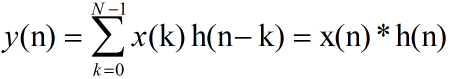
其系统函数为:

FIR滤波器是由一个抽头延迟线加法器和乘法器的集合构成的,每一个乘法器的操作系数就是一个FIR系数。因此,FIR的这种结构也被人们称为抽头延迟线结构。
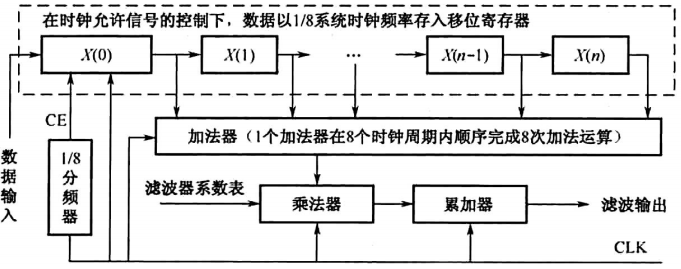
图 串行结构实现FIR滤波器的结构图
02matlab仿真
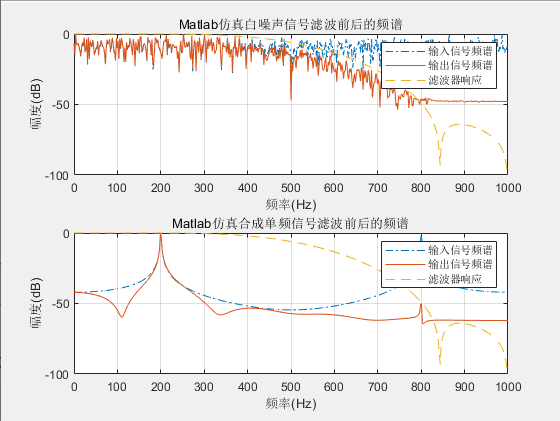
a.设计一个串行fir滤波器,结果显示未量化的实线以及12bit系数量化的虚线,其中虚线才作为真正的滤波器。

%matlab实现一个串行fir滤波器 function hn=serial_fir N=16; %滤波器长度 fs=2000; %采样频率 fc=500; %低通滤波器的截止频率 B=12; %量化位数 %生成布莱克曼窗函数; w_kais=blackman(N)'; %采用fir1函数设计FIR滤波器 b_kais=fir1(N-1,fc*2/fs,w_kais); %量化滤波器系数 Q_kais=round(b_kais/max(abs(b_kais))*(2^(B-1)-1)) hn=Q_kais; %转化成16进制数补码 Q_h=dec2hex(Q_kais+2^B*(Q_kais<0)) %求滤波器的幅频响应 m_kais=20*log(abs(fft(b_kais,1024)))/log(10); m_kais=m_kais-max(m_kais); Q_kais=20*log(abs(fft(Q_kais,1024)))/log(10); Q_kais=Q_kais-max(Q_kais); %设置幅频响应的横坐标单位为Hz x_f=[0:(fs/length(m_kais)):fs/2]; %显示正频率部分的幅频响应 m5=m_kais(1:length(x_f)); m6=Q_kais(1:length(x_f)); %绘制幅频响应曲线 plot(x_f,m5,'-',x_f,m6,'--'); xlabel('频率(Hz)');ylabel('幅度(dB)'); legend('未量化','12bit量化'); grid;

使用这个滤波器进行对噪声的滤波仿真以及对混频信号滤波的仿真:

f1=200; %信号1频率为200Hz f2=800; %信号2频率为800Hz Fs=2000; %采样频率为2KHz N=12; %量化位数 %产生信号 t=0:1/Fs:1; c1=2*pi*f1*t; c2=2*pi*f2*t; s1=sin(c1);%产生正弦波 s2=sin(c2);%产生正弦波 s=s1+s2; %产生两个单载波合成后的信号 %产生随机序列信号 noise=randn(1,length(t));%产生高斯白噪声序列 %归一化处理 noise=noise/max(abs(noise)); s=s/max(abs(s)); %12比特量化 Q_noise=round(noise*(2^(N-1)-1)); Q_s=round(s*(2^(N-1)-1)); %调用自已设计的滤波器函数对信号进行滤波 hn=serial_fir; Filter_noise=filter(hn,1,Q_noise); Filter_s=filter(hn,1,Q_s); %求信号的幅频响应 m_noise=20*log(abs(fft(Q_noise,1024)))/log(10); m_noise=m_noise-max(m_noise); m_s=20*log(abs(fft(Q_s,1024)))/log(10); m_s=m_s-max(m_s); %滤波后的幅频响应 Fm_noise=20*log(abs(fft(Filter_noise,1024)))/log(10); Fm_noise=Fm_noise-max(Fm_noise); Fm_s=20*log(abs(fft(Filter_s,1024)))/log(10); Fm_s=Fm_s-max(Fm_s); %滤波器本身的幅频响应 m_hn=20*log(abs(fft(hn,1024)))/log(10); m_hn=m_hn-max(m_hn); %设置幅频响应的横坐标单位为Hz x_f=[0:(Fs/length(m_s)):Fs/2]; %只显示正频率部分的幅频响应 mf_noise=m_noise(1:length(x_f)); mf_s=m_s(1:length(x_f)); Fmf_noise=Fm_noise(1:length(x_f)); Fmf_s=Fm_s(1:length(x_f)); Fm_hn=m_hn(1:length(x_f)); %绘制幅频响应曲线 subplot(211) plot(x_f,mf_noise,'-.',x_f,Fmf_noise,'-',x_f,Fm_hn,'--'); xlabel('频率(Hz)');ylabel('幅度(dB)');title('Matlab仿真白噪声信号滤波前后的频谱'); legend('输入信号频谱','输出信号频谱','滤波器响应'); grid; subplot(212) plot(x_f,mf_s,'-.',x_f,Fmf_s,'-',x_f,Fm_hn,'--'); xlabel('频率(Hz)');ylabel('幅度(dB)');title('Matlab仿真合成单频信号滤波前后的频谱'); legend('输入信号频谱','输出信号频谱','滤波器响应'); grid; %将生成的数据以十进制数据格式写入txt文件中 fid=fopen('G:\test\serial_fir\doc\int_noise.txt','w'); fprintf(fid,'%8d\r\n',Q_noise); fprintf(fid,';'); fclose(fid); fid=fopen('G:\test\serial_fir\doc\int_s.txt','w'); fprintf(fid,'%8d\r\n',Q_s); fprintf(fid,';'); fclose(fid); %将生成的数据以二进制数据格式写入txt文件中 fid=fopen('G:\test\serial_fir\doc\bin_noise.txt','w'); for i=1:length(Q_noise) B_noise=dec2bin(Q_noise(i)+(Q_noise(i)<0)*2^N,N) for j=1:N if B_noise(j)=='1' tb=1; else tb=0; end fprintf(fid,'%d',tb); end fprintf(fid,'\r\n'); end fprintf(fid,';'); fclose(fid); fid=fopen('G:\test\serial_fir\doc\bin_s.txt','w'); for i=1:length(Q_s) B_s=dec2bin(Q_s(i)+(Q_s(i)<0)*2^N,N) for j=1:N if B_s(j)=='1' tb=1; else tb=0; end fprintf(fid,'%d',tb); end fprintf(fid,'\r\n'); end fprintf(fid,';'); fclose(fid);
这里的噪声以及混频需要matlab生成,并将滤波前相关波形生成十进制数据转换为二进制,其中二进制文本可以用在fpga仿真程序的读取。
其中matlab生成的滤波前的数据bin_noise以及bin_s两个文本,用在fpga仿真程序中。
03fpga实现
这里设计15阶(长度为16),传统抽头延迟线需要16次乘法和15次加法。
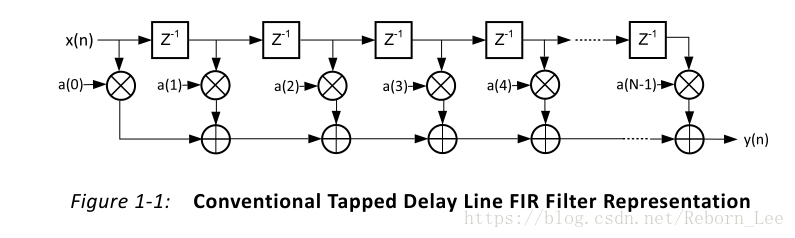
因此这里考虑到FIR滤波器的对称性,可以使得8次乘法和16次加法。
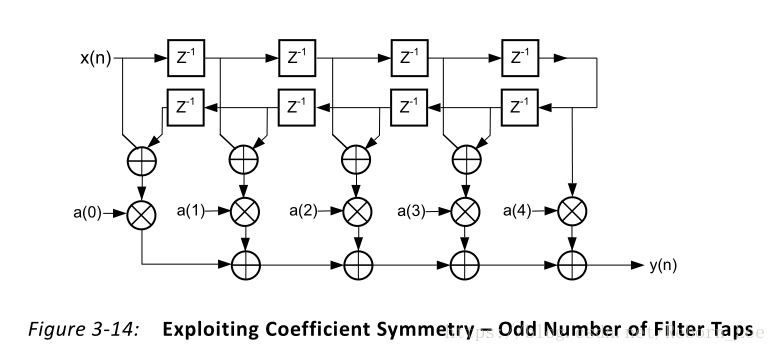
设计要点:
1、代码中coe是滤波器系数a(0) a(1) a(2) a(3)...
2、8次乘法
1 always @(posedge clk or posedge rst) 2 if (rst) 3 begin 4 add_a <= 13'd0; 5 add_b <= 13'd0; 6 coe <= 12'd0; 7 end 8 else 9 begin 10 if (count==3'd0) 11 begin 12 add_a <= {Xin_Reg[0][11],Xin_Reg[0]}; 13 add_b <= {Xin_Reg[15][11],Xin_Reg[15]}; 14 coe <= 12'h000;//c0 15 end 16 else if (count==3'd1) 17 begin 18 add_a <= {Xin_Reg[1][11],Xin_Reg[1]}; 19 add_b <= {Xin_Reg[14][11],Xin_Reg[14]}; 20 coe <= 12'hffd; //c1 21 end 22 else if (count==3'd2) 23 begin 24 add_a <= {Xin_Reg[2][11],Xin_Reg[2]}; 25 add_b <= {Xin_Reg[13][11],Xin_Reg[13]}; 26 coe <= 12'h00f; //c2 27 end 28 else if (count==3'd3) 29 begin 30 add_a <= {Xin_Reg[3][11],Xin_Reg[3]}; 31 add_b <= {Xin_Reg[12][11],Xin_Reg[12]}; 32 coe <= 12'h02e; //c3 33 end 34 else if (count==3'd4) 35 begin 36 add_a <= {Xin_Reg[4][11],Xin_Reg[4]}; 37 add_b <= {Xin_Reg[11][11],Xin_Reg[11]}; 38 coe <= 12'hf8b; //c4 39 end 40 else if (count==3'd5) 41 begin 42 add_a <= {Xin_Reg[5][11],Xin_Reg[5]}; 43 add_b <= {Xin_Reg[10][11],Xin_Reg[10]}; 44 coe <= 12'hef9; //c5 45 end 46 else if (count==3'd6) 47 begin 48 add_a <= {Xin_Reg[6][11],Xin_Reg[6]}; 49 add_b <= {Xin_Reg[9][11],Xin_Reg[9]}; 50 coe <= 12'h24e; //c6 51 end 52 else 53 begin 54 add_a <= {Xin_Reg[7][11],Xin_Reg[7]}; 55 add_b <= {Xin_Reg[8][11],Xin_Reg[8]}; 56 coe <= 12'h7ff; //c7 57 end 58 end
3、16次加法:进行完一个8次乘法,就开始一次移位寄存器,一共有16次移位寄存器
1 always @(posedge clk or posedge rst) 2 if (rst) 3 //初始化寄存器值为0 4 begin 5 for (i=0; i<15; i=i+1) 6 Xin_Reg[i]=12'd0; 7 end 8 else 9 begin 10 if (count==7) 11 begin 12 for (j=0; j<15; j=j+1) 13 Xin_Reg[j+1] <= Xin_Reg[j]; 14 Xin_Reg[0] <= Xin; 15 end 16 end
04fpga仿真
本次实战未实现fpga的仿真,只有matlab对噪声以及混频进行滤波仿真。
05提出问题
1、诸如这两条代码是什么意思?
add_a <= {Xin_Reg[0][11],Xin_Reg[0]};
add_b <= {Xin_Reg[15][11],Xin_Reg[15]};
解答:
reg [11:0] Xin_Reg[15:0];,这里变量Xin_Reg是16个,每一个有12位。
这里的操作add_a <= {Xin_Reg[0][11],Xin_Reg[0]};就是在第0个Xin_Reg的第12位,拼接多一位,然后赋给13位的add_a。
同理可得第二个操作。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号