单目相机成像过程
单目相机成像过程
01 理想情况下相机成像模型
在理想情况下,相机成像模型可以看作是小孔成像模型:
| 相机成像模型 |
为了便于计算,我们将像平面进行翻转,它们在数学上是等价的,并且相机硬件会自动帮我们处理,我们假设成像平面翻转到了相机光心的正前方。相机模型如下,其主要包含4个坐标系:
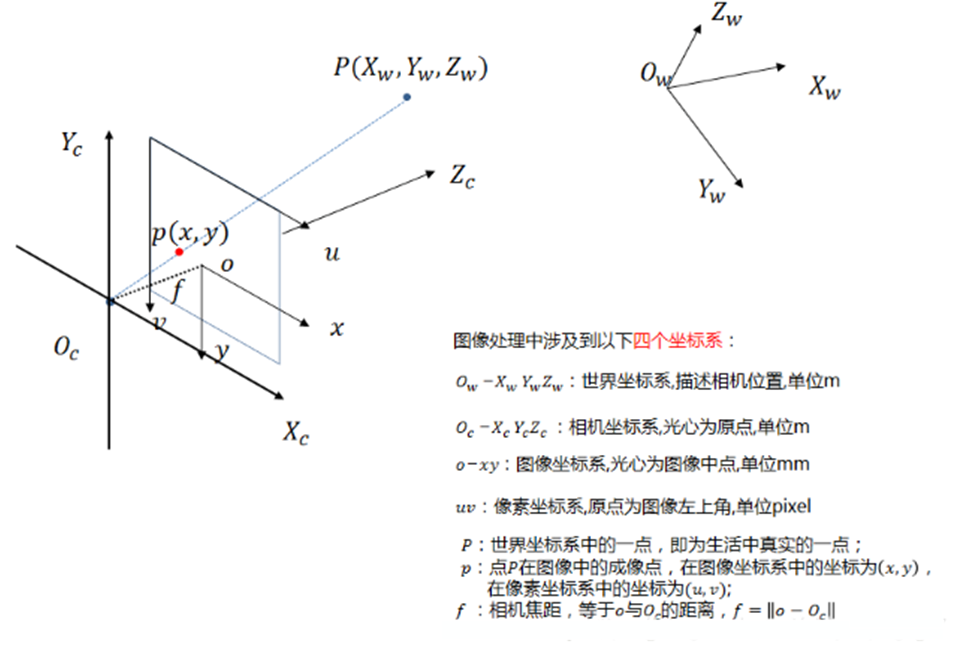 |
|---|
| 图1 相机程序系统中的四大坐标系 |
此外,还有一个归一化平面,其实际是图像坐标系的等比缩放,也就是当 \(f=1\)的情况,主要是便于公式推导,它与图像坐标系是等比缩放关系,只需要乘以 \(f\) 即可完成相互转换。
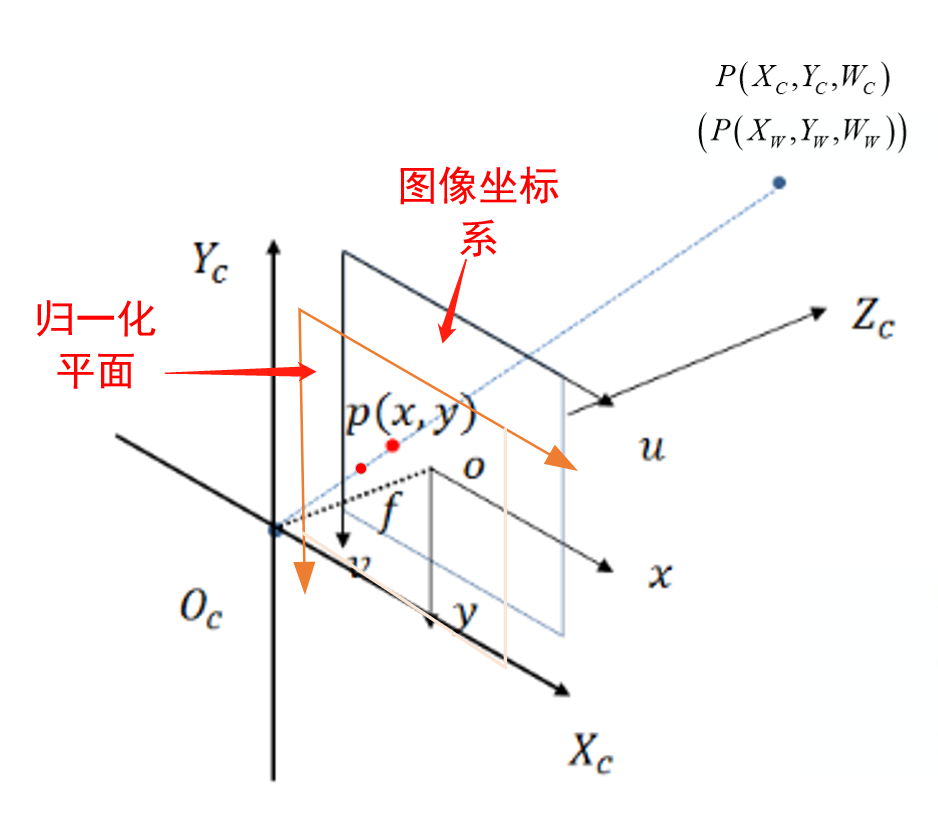 |
|---|
| 图2 归一化平面(坐标系)与图像坐标系关系 |
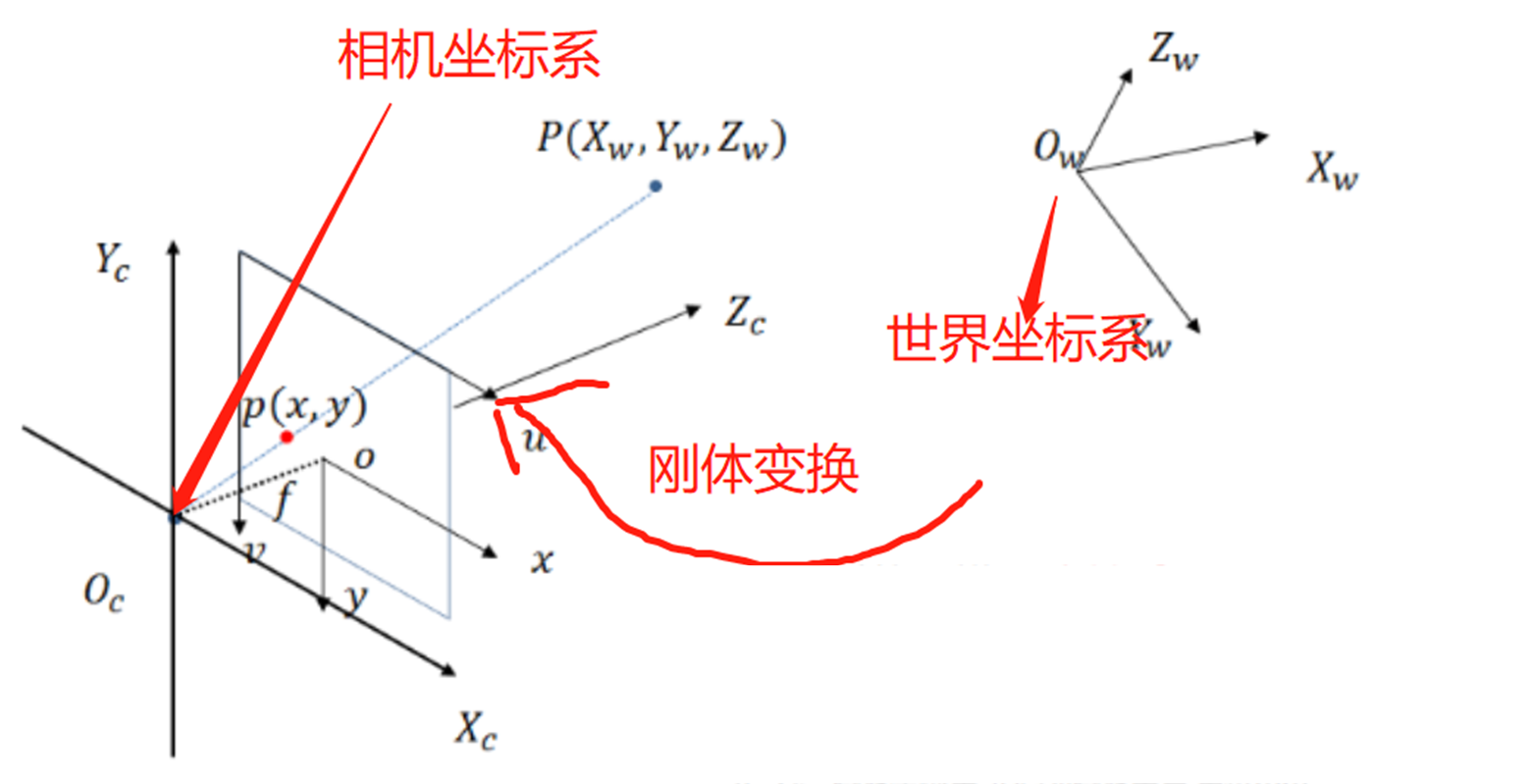
1)世界坐标系 -> 相机坐标系
 |
|---|
| 图3 世界坐标系 -> 相机坐标系(刚体变换) |
假设该点世界坐标系为 \([X_W,Y_W,Z_W]^T\),世界坐标系到相机坐标系的变换是一个刚体变换,那么同样的该点,在相机坐标系下的坐标 \([X_C,Y_C,Z_C]^T\) 如下:
为了将旋转矩阵和平移矩阵两个矩阵形式统一,需要引入齐次坐标表示形式:
2)相机坐标系 -> 图像坐标系
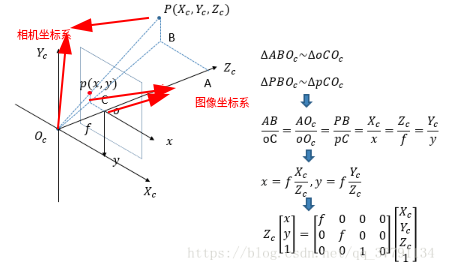
从相机坐标系 \([X_C,Y_C, Z_C,1]^T\) 到 图像坐标系 \([x,y]^T\)(成像平面) 的变换是个相似三角形变换,推导如下:
 |
|---|
| 图4 相机坐标系 -> 图像坐标系(相似三角形) |
总结:
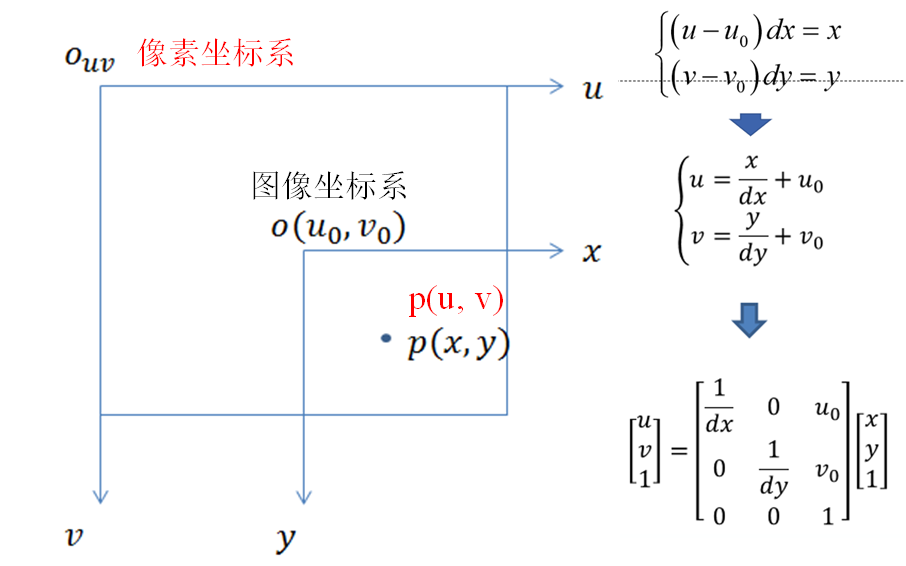
3)图像坐标系 -> 像素坐标系
图像坐标系和像素坐标系处在同一平面,但是有两点不同:
- 坐标原点不同:图像坐标系,成像平面的中心;像素坐标系,成像平面左上角;
- 单位不同:图像坐标系,单位mm,属于物理单位;像素坐标系,单位pixel(\(1 \ pixel= dx \ or \ dy \ mm\)),平常描述一个像素点都是几行几列;
它们之间的转换关系如下,包含平移与缩放两个变换:
总结:
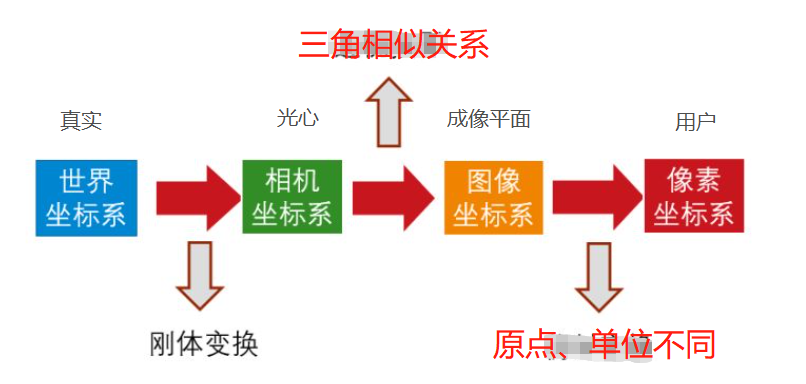
4)总结
从世界坐标系到像素坐标系的转换关系如下:
-
世界坐标系到相机坐标系:
\[\underbrace {\left[ {\begin{array}{*{20}{c}} {{X_C}}\\ {{Y_C}}\\ {{Z_C}}\\ 1 \end{array}} \right]}_{相机坐标系} = \underbrace {\left[ {\begin{array}{*{20}{c}} {{R_{3 \times 3}}}&{{T_{3 \times 1}}}\\ 0&1 \end{array}} \right]}_{刚体变换}\underbrace {\left[ {\begin{array}{*{20}{c}} {{X_W}}\\ {{Y_W}}\\ {{Z_W}}\\ 1 \end{array}} \right]}_{世界坐标系} \] -
相机坐标系到图像坐标系:
\[{Z_c}\underbrace {\left[ {\begin{array}{*{20}{c}} x\\ y\\ 1 \end{array}} \right]}_{\rm{图像坐标系}} = \underbrace {\left[ {\begin{array}{*{20}{c}} f&0&0&0\\ 0&f&0&0\\ 0&0&1&0 \end{array}} \right]}_{相似三角}\underbrace {\left[ {\begin{array}{*{20}{c}} {{X_C}}\\ {{Y_C}}\\ {{Z_C}}\\ 1 \end{array}} \right]}_{相机坐标系} \] -
图像坐标系到像素坐标系:
\[\underbrace {\left[ {\begin{array}{*{20}{c}} u\\ v\\ 1 \end{array}} \right]}_{像素坐标系} = \underbrace {\left[ {\begin{array}{*{20}{c}} {\frac{1}{{dx}}}&0&{{u_0}}\\ 0&{\frac{1}{{dy}}}&{{v_0}}\\ 0&0&1 \end{array}} \right]}_{平移+缩放}\underbrace {\left[ {\begin{array}{*{20}{c}} x\\ y\\ 1 \end{array}} \right]}_{图像坐标系} \]
将之前所有的变换合并,可以得到:
将它们相乘后化简:
以上是理想情况下世界坐标系到像素坐标系的转换,而由于相机制造工艺的原因,其成像过程中难免存在着畸变,在后续构建精确的三维重建算法前,我们要对相机的畸变进行矫正,以提高算法重建的精度,这一步骤也称为相机标定。
02 考虑畸变情况下相机成像模型
相机畸变主要有两种类型:径向畸变 和 切向畸变,我们分别介绍这两种情况。
1)径向畸变
原因:在相机制造过程中,很难保证镜头的厚度完全均匀,由于制造工艺的原因,通常为这种情况为中间厚、边缘薄,因而光线在远离透镜中心的地方,会发生更大程度的扭曲,这种现象在鱼眼相机(桶形畸变)中尤为明显。
径向畸变主要有两种类型:枕型畸变和桶型畸变,示意图如下:
 |
 |
|---|---|
 |
 |
| 桶型畸变 | 枕形畸变 |
它们可以由 \(k_1,k_2\) 构成的下列数学公式描述:
其中:
- \(r\) 为曲率半径,有:\(r^2 =x^2 + y^2\);
- \(k_1,k_2,k_3\) 为径向畸变系数;
- \(x, y\) 为发生畸变后角点的坐标,也就是我们实际看到的;
- \(x',y'\) 为畸变矫正,也就是去除畸变后的正确坐标;
注:这里无论是 \(x, y,x',y'\),其均为归一化平面上角点的坐标。
通常:我们只用 \(k_1,k_2\) 来矫正相机,对于畸变较小的图像中心区域,主要是 \(k_1\) 在起作用,对于畸变较大的图像边缘区域,主要是 \(k_2\) 在起作用,而对于鱼眼相机这类广角相机,我们才会用 \(k_3\)。需要注意的是,这里并不是用的系数越多,整个矫正结果越精确,我们应该考虑相机的实际情况。
2)切向畸变
原因:切向畸变产生的原因在于相机在制造过程中,成像平面与透镜平面不平行,产生了透视变换。
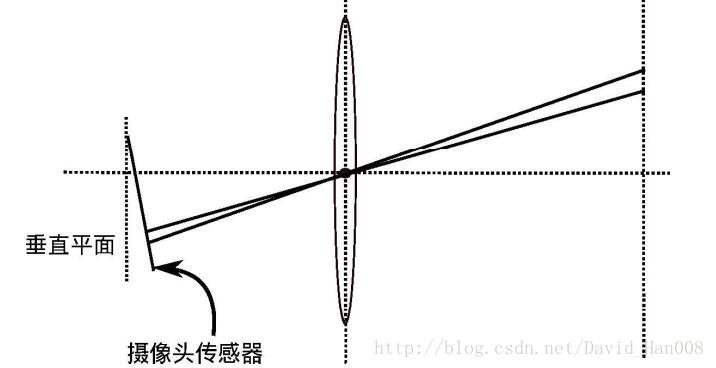
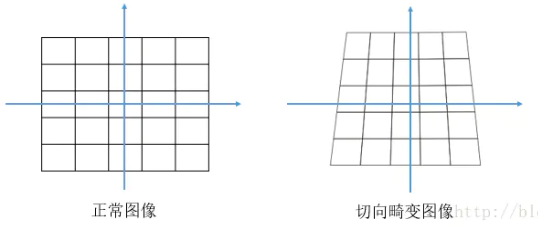
这种畸变可以由以下公式描述,它也与距离图像中心的距离半径有关:
其中:\(p_1,p_2\) 称为切向畸变矫正系数,其它的含义与径向畸变中公式相同。
3)合并考虑畸变
原因:其实也很简单,两种畸变是同时发生在成像过程中的,发生的原因也是相互独立的,而且也都是关于距离的表达式,你似乎也找不到更好的方式来综合考虑这两种误差,实践证明,这种合并考虑畸变的情况效果还不错。
将径向畸变和切向畸变合并,只需要将两个畸变矫正直接加起来即可,公式如下:
其中:
- \(k_1,k_2,k_3\) 为径向畸变系数;
- \(p_1,p_2\) 为切向畸变系数;
不过在此之前,我们特别注意一点,相机畸变现象发生的位置:
- 世界坐标系 -> 相机坐标系,刚体变换,不存在畸变现象;
- 相机坐标系 -> 图像坐标系,也就是成像过程,理想情况下是相似三角形,但实际由于相机制造、装配的原因,成像过程存在畸变现象;
- 图像坐标系 -> 像素坐标系,坐标原点、单位不同,仅仅平移与缩放,不存在畸变现象;
03 成像过程总结
现在,我们将这些公式进行整理,假设:
- 某点世界坐标系为\(P(X_W,Y_W,Z_W)\);
- 对应的实际得到的像素坐标系为 \(P(u,v)\)(未矫正的);
- 正确的像素坐标为 \(P(u',v')\);
- 假设我们已知畸变系数 \(k_1,k_2,k_3,p_1,p_2\);
那么从世界坐标系 \(P(X_W,Y_W,Z_W)\) 到正确的像素坐标系 \(P(u',v')\) 的推导如下,对于像素坐标系下某点 \(P(u,v)\),有:
-
像素坐标系 -> 归一化坐标系
这个变换仅仅是平移与缩放,不存在畸变,因而只需要一个逆变换,归一化坐标 \(P=(x,y)^T\) 推导如下:
\[\begin{array}{c} \underbrace {\left[ {\begin{array}{*{20}{c}} u\\ v\\ 1 \end{array}} \right]}_{像素坐标} = \underbrace {\left[ {\begin{array}{*{20}{c}} {\frac{1}{{dx}}}&0&{{u_0}}\\ 0&{\frac{1}{{dy}}}&{{v_0}}\\ 0&0&1 \end{array}} \right]}_{平移+缩放}\underbrace {\left( {\underbrace {\left[ {\begin{array}{*{20}{c}} x\\ y\\ {1/f} \end{array}} \right]}_{归一化坐标} \times f} \right)}_{图像坐标} \\ \Downarrow \\ \underbrace {\left[ {\begin{array}{*{20}{c}} x\\ y\\ {1/f} \end{array}} \right]}_{归一化坐标} = \underbrace {\left( {{{\left[ {\begin{array}{*{20}{c}} {\frac{1}{{dx}}}&0&{{u_0}}\\ 0&{\frac{1}{{dy}}}&{{v_0}}\\ 0&0&1 \end{array}} \right]}^{ - 1}}\underbrace {\left[ {\begin{array}{*{20}{c}} u\\ v\\ 1 \end{array}} \right]}_{像素坐标}} \right)}_{图像坐标}/f \end{array} \] -
归一化坐标系(带畸变的) -> 归一化坐标系(畸变矫正后)
在前一成像过程,也就是相机坐标系到归一化平面透射中,相机发生了畸变,因而我们需要将实际的归一化坐标 \(P=(x,y)^T\) 纠正到理想的无畸变归一化坐标 \(P=(x',y')^T\):
\[\left[ {\begin{array}{*{20}{c}} {x'}\\ {y'}\\ {1/f} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\left( {1 + {k_1}{r^2} + {k_2}{r^4} + {k_3}{r^6}} \right)x + 2{p_1}xy + {p_2}\left( {{r^2} + 2{x^2}} \right)}\\ {\left( {1 + {k_1}{r^2} + {k_2}{r^4} + {k_3}{r^6}} \right)y + 2{p_2}xy + {p_1}\left( {{r^2} + 2{y^2}} \right)}\\ {1/f} \end{array}} \right] \] -
归一化坐标系(理想)-> 相机坐标系
理想的无畸变归一化坐标 \(P=(x',y')\) 到相机坐标系,它们是相似三角形关系:
\[{Z_c}\underbrace {\left( {\underbrace {\left[ {\begin{array}{*{20}{c}} {x'}\\ {y'}\\ 1/f \end{array}} \right]}_{归一化坐标系(准确)} \cdot f} \right)}_{图像坐标} = \underbrace {\left[ {\begin{array}{*{20}{c}} f&0&0&0\\ 0&f&0&0\\ 0&0&1&0 \end{array}} \right]}_{相似三角形}\underbrace {\left[ {\begin{array}{*{20}{c}} {{X_C}}\\ {{Y_C}}\\ {{Z_C}}\\ 1 \end{array}} \right]}_{相机坐标} \\ \Downarrow \\ \left[ {\begin{array}{*{20}{c}} {{X_c}}\\ {{Y_c}}\\ {{Z_c}}\\ 1 \end{array}} \right] = f \cdot {Z_c} \cdot {\left[ {\begin{array}{*{20}{c}} f&0&0&0\\ 0&f&0&0\\ 0&0&1&0 \end{array}} \right]^{ - 1}}\left[ {\begin{array}{*{20}{c}} {x'}\\ {y'}\\ {1/f} \end{array}} \right] \]注:这里 \(3 \times 4\) 矩阵的逆是伪逆。
-
相机坐标系 -> 世界坐标系
相机坐标系到世界坐标系,仅仅是之前刚体变换的反变换:
\[\underbrace {\left[ {\begin{array}{*{20}{c}} {{X_C}}\\ {{Y_C}}\\ {{Z_C}}\\ 1 \end{array}} \right]}_{相机坐标系} = \underbrace {\left[ {\begin{array}{*{20}{c}} {{R_{3 \times 3}}}&{{T_{3 \times 1}}}\\ 0&1 \end{array}} \right]}_{刚体变换}\underbrace {\left[ {\begin{array}{*{20}{c}} {{X_W}}\\ {{Y_W}}\\ {{Z_W}}\\ 1 \end{array}} \right]}_{世界坐标系} \\ \Downarrow \\ \left[ {\begin{array}{*{20}{c}} {{X_W}}\\ {{Y_W}}\\ {{Z_W}}\\ 1 \end{array}} \right] = {\left[ {\begin{array}{*{20}{c}} {{R_{3 \times 3}}}&{{T_{3 \times 1}}}\\ 0&1 \end{array}} \right]^{ - 1}}\left[ {\begin{array}{*{20}{c}} {{X_C}}\\ {{Y_c}}\\ {{Z_c}}\\ 1 \end{array}} \right] \]
所以,我们只需要将上述的四个公式合并起来即可,像素坐标系\(P=(u,v)\)转换到世界坐标系 \(P=(X_W,Y_W,Z_W)\)。
04 思考问题
现在的问题是,我们如何求得这些畸变系数 \(k_1,k_2,k_3,p_1,p_2\)?得到这些系数之后,我们就能建立像素坐标系与世界坐标系的映射。这个问题可以由张正友标定法来实现。
对于张正友标定法的原理,略微有些复杂,在下一节推送中,我们从它的实现开始讲起,然后如果你们有兴趣,可以看我们的拓展阅读《张正友标定法数学基础及原理推导》。
先回过头来看前面的式子,我们可以看到,即使考虑了畸变,从像素坐标系到世界坐标系的转换,其实还是一些乘法运算,但是这里有两个问题需要大家思考:
1)问题一
对于考虑了畸变的相机模型,世界坐标系与像素坐标系之间的转换公式,其实是存在一个问题的:不能写成完全矩阵\(x,y\) 的乘法形式。因为相机模型的切向畸变部分包含非线性项 \(xy,x^2,y^2\):
有人说,这样似乎也没什么问题嘛,无非是计算速度慢一点而已,但事情不是这样的,矩阵方程里存在着非线性项,而且还有一个加法,我们那些关于方程组解、求特征值、正定、半正定、正交这些理论武器,全部都失去作用了。
事实上,一些质量较好的工业相机,切向畸变都是很小的(话说,相机都不准,你拿它做什么精确的三维重建…),张正友标定法在初始的时候即假设相机不存在径向畸变(之后会求),也就是 \(p_1,p_2\) 都等于零,另外同样\(k3=0\)。这样的好处在于,考虑畸变的相机模型,在初期跟理想模型的差别在于乘以一个常数项,整个式子就可以写为一个单应性矩阵的形式,方便我们对方程组进行优化:
其中:
- \(s\) 称为尺度因子;
- $\tilde m $ 为像素坐标系,$\tilde M $ 为世界坐标系;
- \(A\) 为单应性矩阵;
- \([R_{3 \times 3} \ T_{3\times1}]\) 是外参矩阵;
2)问题二
还有个问题,假设我们得到了这些畸变系数,能否由像素坐标系推导到世界坐标系?事实上是不能的,比如下面这种图:
 |
 |
|---|---|
| 图a 单目相机失真 | 图2 单目相机模型 |
光心 \(O_c\) 与\(P(X_C,Y_C,Z_C)\) 的整条连线上的三维点,在成像平面的像点均在点 \(p(x,y)\) 上。所以在单目相机的标定方法中,甚至不需要知道棋盘格的实际大小也能完成相机的标定。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号