CF15E
这个题解最后的式子写错了，看最后
（注意一下算层数要 n /= 2 ！）
这里面关于 \(ans\) 的用法：为什么是 \(2\times ans^2+8\times ans+10\) 已经讲得很清楚了。
主要补充一下怎么求 \(ans\) 的部分。
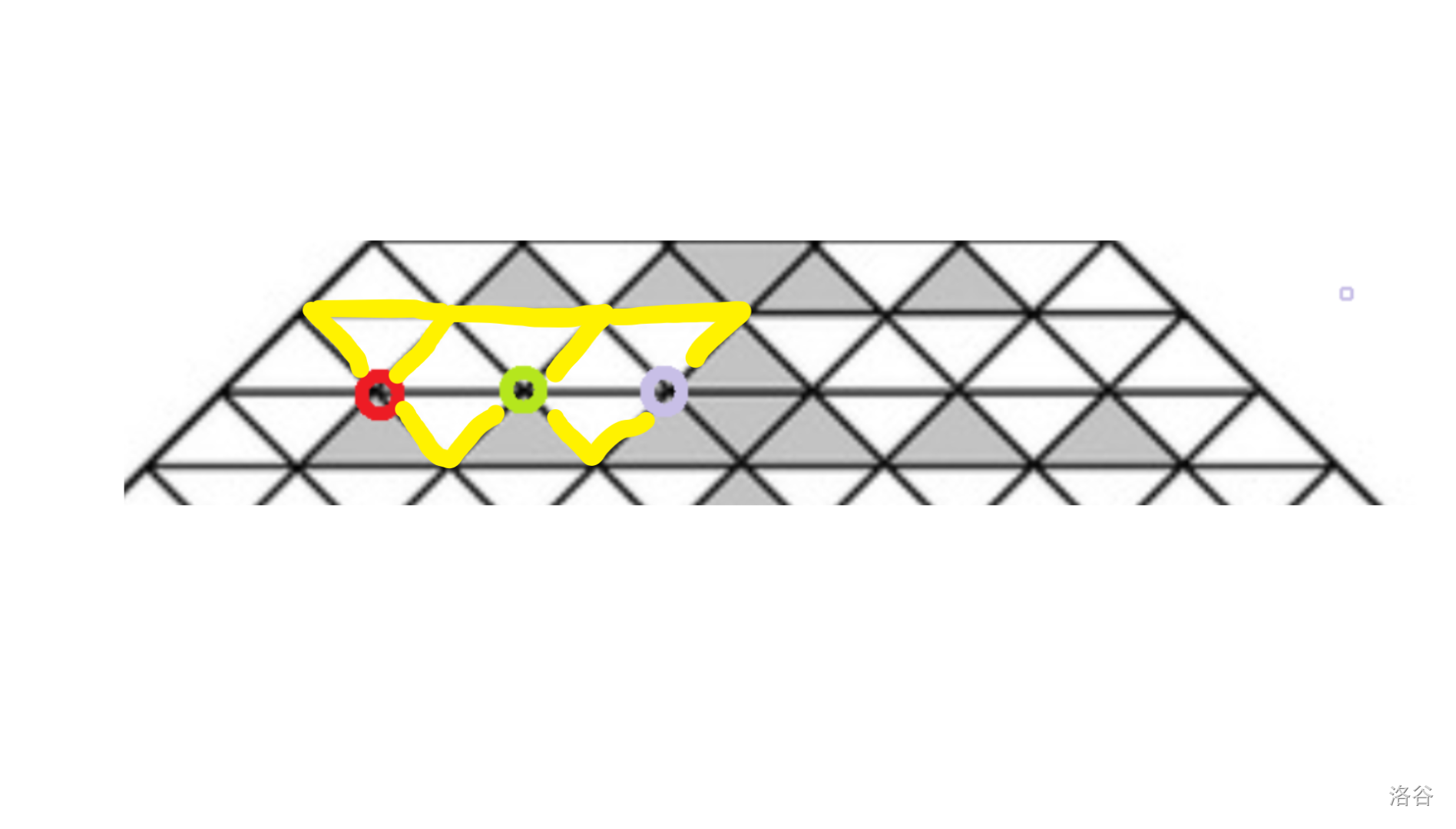
如图，三个决策点的所在部分可以视作一个三角形 + 若干个斜着的梯形。
经过这一层的方案数 = 只经过三角形的数量 + 经过三角形和一个梯形的数量 + ... + 经过所有梯形的数量。
如果只经过三角形，有 \(1\) 种。
如果经过三角形和一个梯形（即红点和绿点），有 \(4\) 种。
如果两个梯形，\(8\) 种。
观察得出，如果是 \(x\) 个梯形，就有 \(2^{x+1}\) 种。
这是为什么呢？因为每个梯形的下半部分有 \(2\) 种可能通往下一个梯形的边界。同时最后一个梯形有 \(2\) 种可能回去，除了最后一个梯形，都只能走上边界回去。
所以这一层的方案数，假设有 \(k\) 个梯形，答案就是 \(1+\displaystyle\sum_{i=1}^k 2^{i+1}=1+\sum_{i=2}^{k+1}2^i=\sum_{i=0}^{k+1}2^i-2=2^{k+2}-3\) 种可能。
如果 \(n\) 那一层（这里的层指的是原本的层）是很多个黑三角的，简单；如果只有一个黑三角，还要特判一下最后一层。
【一开始想错了的点】
题解最后的式子应该是 \(ans=\displaystyle\sum_{i=2}^k[4\times \prod_{j=2}^i(2^j-3)]\)
同时再解释一下最后的 \(ans=\displaystyle\sum_{i=2}^k[4\times \prod_{j=2}^i(2^j-3)]\)，其中最外层的求和是分类，分的类是 \(ans\) 走到第几层就回来；内层的累乘是分步，意思是每一层的方案数分别乘起来；那个 \(4\) 是最后一层返回的方案数。
