P8293 序列变换题解
先将括号序列建树。
具体而言,假设当前根结点为 \(rt\),当前括号序列为 \(s\)。若 \(s\) 能分成 \(cnt\) 组括号,则 \(rt\) 有 \(cnt\) 个儿子。对于第 \(i\) 个儿子,以它为新根结点,第 \(i\) 组括号为新括号序列,递归建树。
例如 (()())(()) 建出来的树长这样:
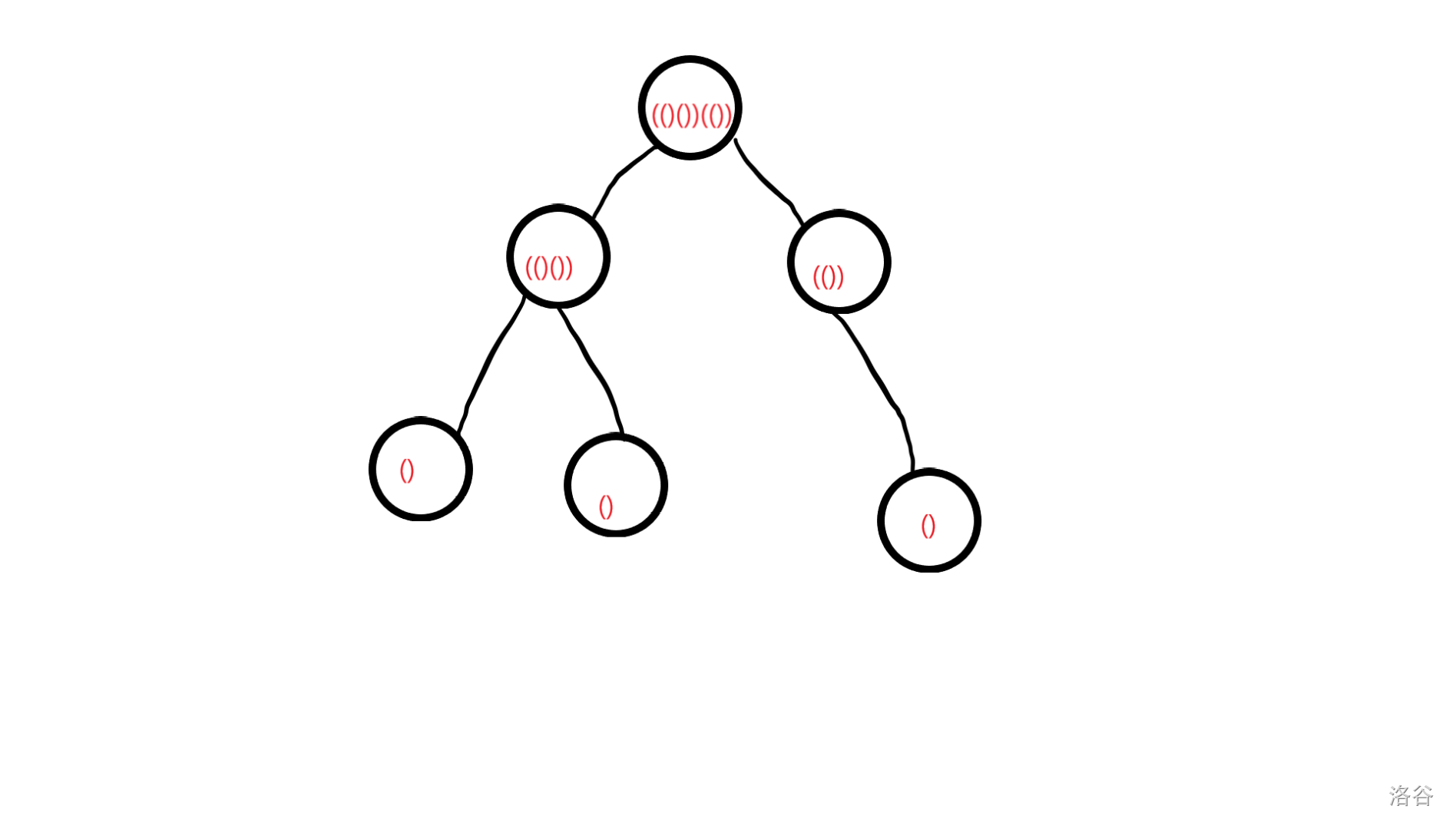
同时,在每个结点上记录它代表的括号序列中第一个左括号的权值,作为这个结点的权值。\(u\) 的权值记为 \(a_u\)。
题目中给出的两个操作可以对应到树上的操作。
操作一:交换相邻两颗子树,无代价。
操作二:选定两个儿子 \(c,d\),将 \(d\) 作为 \(c\) 的儿子,\(d\) 的子孙们都变成 \(u\) 的儿子。代价为 \(a_c\times x+a_d\times y\)。称为 “下降” 操作。
形象点:
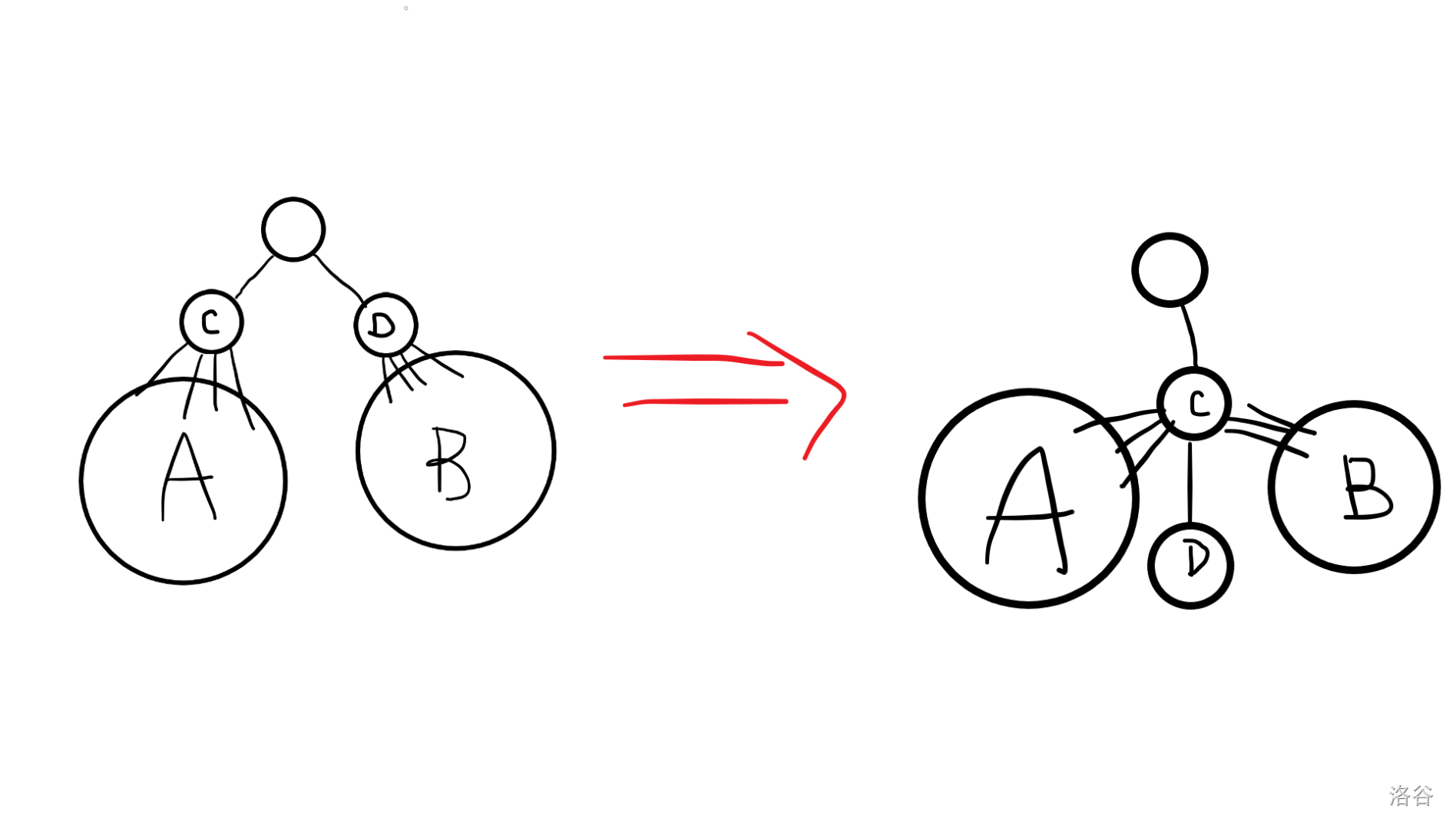
题目最终的要求是花费最小的代价让这棵树变成链。
先给出一个结论:一定存在最优解,先对浅的结点下降,再对深的结点下降。
证明很简单,因为先下降浅的结点的后续可能性包含了所有先下降深的结点的后续可能性。所以先下降浅的结点一定不差。
下面分类讨论。
\(x=y=0\) 时很显然,答案为 \(0\)。
\(x=y=1\) 时,给出一个贪心方法。假设当前层有 \(t\) 个结点 \(v_1\sim v_t\),且 \(a_{v_1}\le\dots\le a_{v_t}\)。我们先依次选定 \((v_1,v_2),(v_1,v_3),\dots,(v_1,v_{t-1})\),让 \(v_2\sim v_{t-1}\) 下降。然后选定 \((v_1,v_t)\) 让 \(v_1\) 下降。
这一层花费是 \((t-2)v_1+(v_1+v_2+\dots+v_t)\)。
而我们知道这一层总归是需要留下一个结点的。但是如果留下的不是 \(v_t\),可以换成 \(v_t\),这样更深的层花费会更少。因此按照这个贪心就行了。
\(x=0,y=1\) 时,每一层的花费是这一层所有要下降的结点权值和。如果选择下降 \(v_1\sim v_{t-1}\),不仅本层的花费最小,而且对未来也更优。
最后是 \(x=1,y=0\),这种情况是最难的,因为如果下降权值小的,对未来更优,但是留在本层的要收费,对现在不优;如果下降权值大的,对未来不优。
我们加几个定义:
假设最后链长为 \(n\)。\(cnt[i]\) 表示处理第 \(i\) 层时第 \(i\) 层有多少个结点,\(mn[i]\) 表示处理第 \(i\) 层时权值最小的结点的权值,\(w[i]\) 表示留了一个权值为 \(w[i]\) 的在第 \(i\) 层。
则总修改代价 \(cost = \displaystyle\sum_{i=1}^{n-1} mn[i](cnt[i]-2)+allsum-w[n]\),其中 \(allsum\) 表示所有节点的权值和。
这个式子是怎么推出来的?对于第 \(i\) 层,最终留下 \(w[i]\),最优决策就是让 \(mn[i]\) 把其他结点都下降,然后让 \(w[i]\) 下降 \(mn[i]\)。因此本层的最优决策是 \(mn[i](cnt[i]-2)+w[i]\)。于是总修改代价就是 \(1\sim n-1\) 层的代价求和。
我们的目标是使 \(cost\) 最小,因为 \(allsum\) 为常数,所以就等价于让 \(\sum mn[i](cnt[i]-2)-w[n]\) 最小。
当 \(cnt[i]\ge 3\) 时,我们可以贪心地每次让本层的最小值和最大值都下降,随便留下一个其他的就行了。因为留下哪一个其实对总代价没影响,而下降最小值可以让未来的 \(mn\) 更小,下降最大值可以让 \(w[n]\) 尽可能的大。
于是我们解决了 \(cnt[i]\ge 3\) 的情况,\(cnt[i]=1\) 就结束了,只剩 \(cnt[i]=2\) 的情况。
这个时候我们再补充一个观察:\(cnt\) 数组一旦开始下降,就会一直下降。
为什么呢?因为每一层下降只会减少一个结点,连只减少 \(1\) 都无法挽回,说明下一层没有结点了。既然没有结点,就会一直下降直到成链。
于是 \(cnt[i]=2\) 的情况一定是连续的,也就是某一层 \(cnt=2\),然后两个结点中连着一个结点,这个结点又连着一个 …… 直到某一个结点有两个儿子,\(cnt=3\) 了,这之前 \(cnt=2\)。
我们称 \(cnt=2\) 的部分为上部分,比上部分深的部分为下部分。显然上部分会有一个结点下降到下部分,记这个结点为 \(p\);同时记下部分中最大值为 \(q\)(不包括上部分下来的 \(p\))。上部分与下部分的分界层为 \(l\)。
当 \(p\le q\),总花费为 \(sum_{up}-p+\displaystyle \sum_{i=l}^{n-1}mn[i](cnt[i]-2)+(sum_{down}+p)-q\),其中 \(sum_{up}\) 为上部分的权值之和,\(sum_{down}\) 为下部分的权值之和。手推一下就行。
发现 \(p\) 抵消掉了,\(q\) 和 \(cnt\) 都是固定的,所以我们选择下降最小的下去,这样能让 \(mn\) 更小。
当 \(p>q\),总花费类似刚刚的式子: \(sum_{up}-p+\displaystyle \sum_{i=l}^{n-1}mn[i](cnt[i]-2)+(sum_{down}+p)-p\)。抵消后剩一个 \(-p\),而且因为 \(p>q\),下部分最大的都比 \(p\) 小了,\(p\) 也不可能对 \(mn\) 有贡献了,所以肯定要 \(p\) 越大越好。
至此,\(cnt=2\) 的情况也解决了。那整个问题也就解决了。



