倍增 LCA
【朴素 LCA】
LCA 是树的一个重要概念，意为两结点的最近公共祖先。
先给出朴素求 LCA 的代码。
int get_LCA(int u, int v) {
if (d[u] > d[v])
swap(u, v);
while (d[u] != d[v])
v = p[v];
while (u != v)
u = p[u], v = p[v];
return u;
}
其中 \(d_i\) 表示结点 \(i\) 的深度，\(p_i\) 表示结点 \(i\) 的父节点。
但是，这样最坏情况下需要遍历整棵树，时间复杂度为 \(O(n)\)。
我们需要优化这个过程。
观察可知，时间复杂度太高的瓶颈在于每次都只能往上提一个结点。
那有没有办法可以一次多提一些结点呢？有的。
它就是倍增算法。
【倍增 LCA】
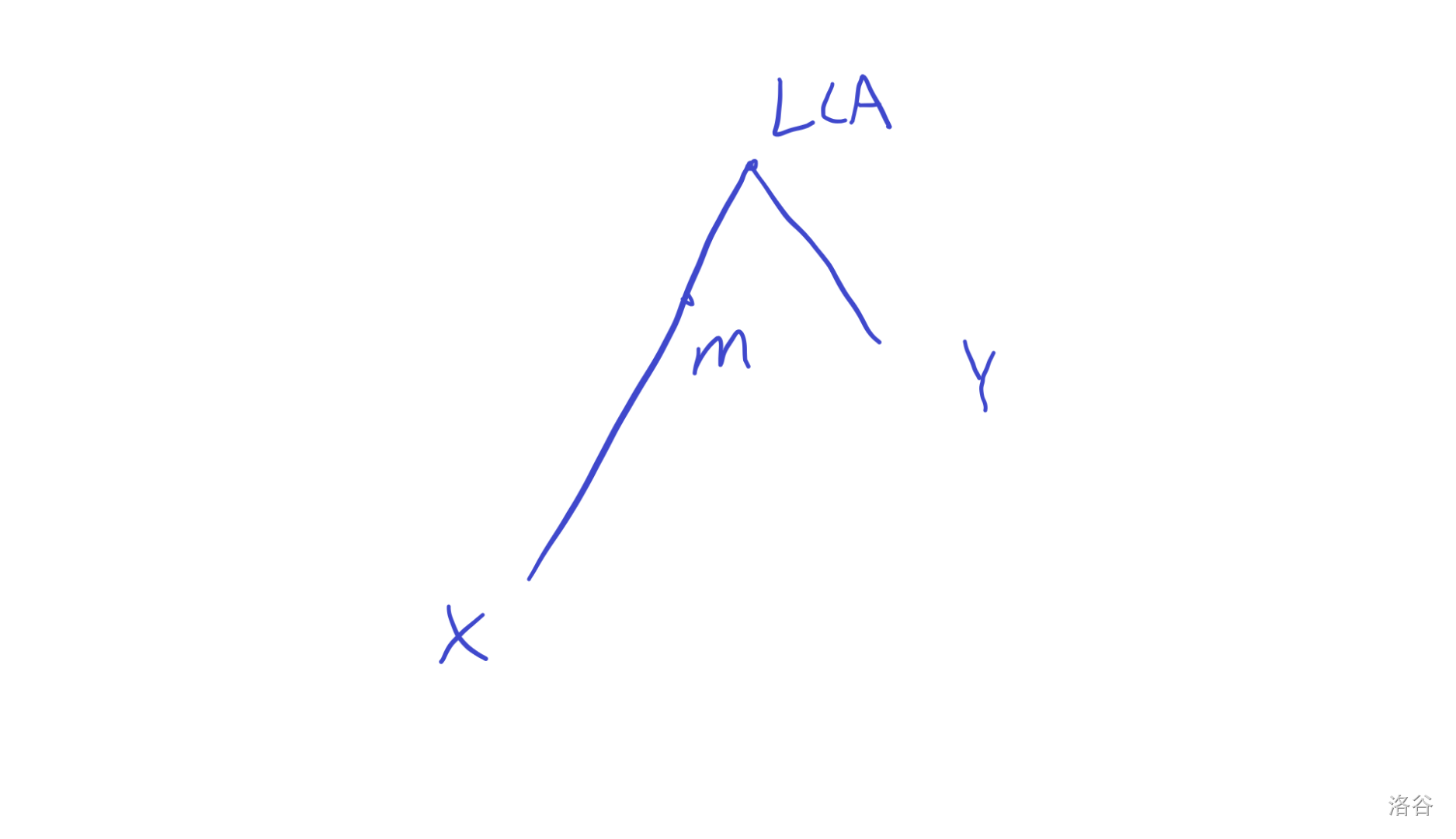
定义 \(f_{i,\;j}\) 为结点 \(i\) 的 \(2^j\) 级祖先。（零级是父结点，一级往上提两个，二级往上提四个，三级提八个，以此类推）
这个数组预处理也很简单：
\(f_{i,j}=f_{f_{i, j-1},j-1}\)，其实就是 \(2^j=2^{j-1}+2^{j-1}\)
看看有了这个数组要怎么求 LCA 。
假设现在要求 \(u\) 和 \(v\) 的 LCA 。
朴素 LCA 分两步：一是使 \(d_u=d_v\)，二是一个一个提。
倍增 LCA 也是一样的步骤，不妨 \(v\) 比 \(u\) 深。
循环 \(i\) 从 \(\log_2^{\;\,n}\) 到 \(0\)。
每次如果 \(d_{f_{v,\;i}} \ge d_u\)，就令 \(v = f_{v,\;i}\)。
这相当于把所差的深度二进制分解了，从高到低遍历每一位。
这时 \(d_u=d_v\)，这里有一个需要注意的点：若 \(u=v\)，返回 \(u\)。
这个特判就是判定 \(u\) 的子树是否包含 \(v\)。
然后我们继续循环 \(i\) 从 \(\log_2^{\;\,n}\) 到 \(0\)。
每次如果 \(f_{u,\;i}\neq f_{v,\;i}\)，则使 \(u=f_{u,\;i}\)，\(v=f_{v,\;i}\)。
可是 LCA 不是 \(u=v\) 吗？为什么是不等于呢？
因为我们没法判断在不在 LCA 上面，所以只好提升到 LCA 下面一个。
也因此我们最后返回的是 \(p_u\) 。
【code】
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
typedef long long ll;
#define elif else if
int n, m, s, d[500005];
vector<int> e[500005];
int pw[25] = {1}, lg[500005] = {0};
int p[25][500005];//p[j][i]为i的2^j代祖先
void srh(int x, int ftr, int dep)//当前点，父节点，深度
{
d[x] = dep, p[0][x] = ftr;
for (int i = 1; i <= 20; i++)
p[i][x] = p[i - 1][p[i - 1][x]];
for (auto i : e[x])
if (i != ftr)
srh(i, x, dep + 1);
}
void init()
{
for (int i = 1; i <= 20; i++)
pw[i] = pw[i - 1] * 2;
for (int i = 1; i <= n; i++)
lg[i] = lg[i / 2] + 1;
// for (int i = 1; i <= 20; i++)
// for (int j = 1; j <= n; j++)
// p[i][j] = p[i - 1][p[i - 1][j]];
}
int anc(int x, int k)//x的k层祖先
{
for (int i = 20; i >= 0; i--)
if (k >= pw[i])
x = p[i][x], k -= pw[i];
return x;
}
int lca(int x, int y)
{
if (d[x] < d[y])
swap(x, y);
x = anc(x, d[x] - d[y]);
if (x == y)
return x;
for (int i = 20; i >= 0; i--)
if (p[i][x] != p[i][y])
x = p[i][x], y = p[i][y];
return p[0][x];
}
int main()
{
cin >> n >> m >> s;
for (int i = 1, x, y; i < n; i++)
cin >> x >> y, e[x].push_back(y), e[y].push_back(x);
init();
srh(s, s, 0);
for (int i = 1, a, b; i <= m; i++)
cin >> a >> b, cout << lca(a, b) << endl;
return 0;
}
【LCA 的扩展】
- 树上路径，可以视作两个点分别走到 LCA。两点距离可以用深度差求出来。
仓鼠找 sugar：两条路径有交点，等价于有一个 LCA 在另一条路上
Misha, Grisha and Underground：
三个点取LCA，一定有两个点先汇合，不妨A、B先，lca(A,B)=X
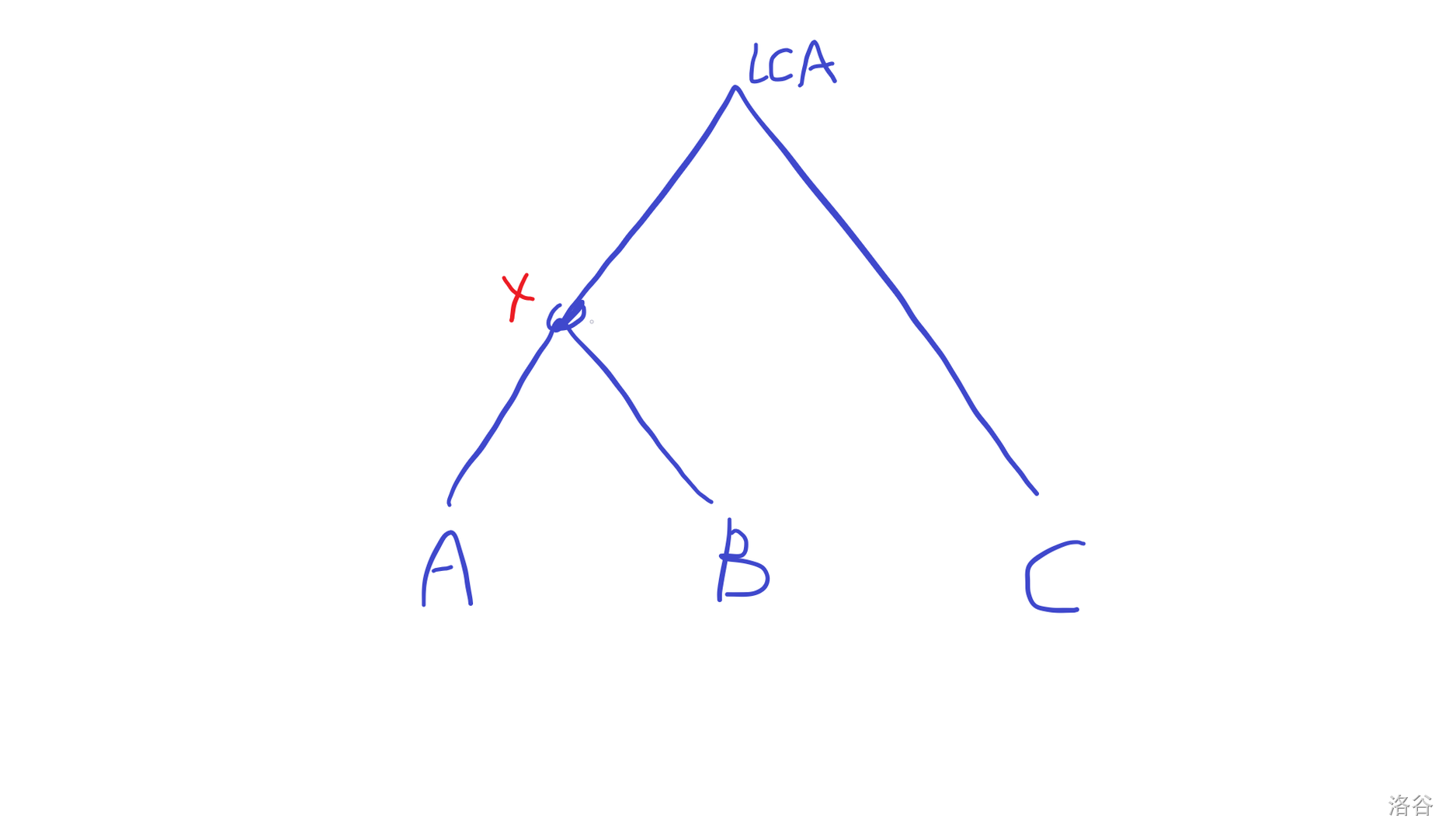
那么三个点之间的路径相当于从X伸出去的三条中走两条。
X到A，X到B，X到C 的距离，求最大值即可。
推论：如果 \(z\) 到 \(x,y\) 的距离相等，则 \(z\) 到 \(x,y\) 的路径一定是先到 \(x,y\) 的中点，再去 \(x,y\) 。
推论证明：
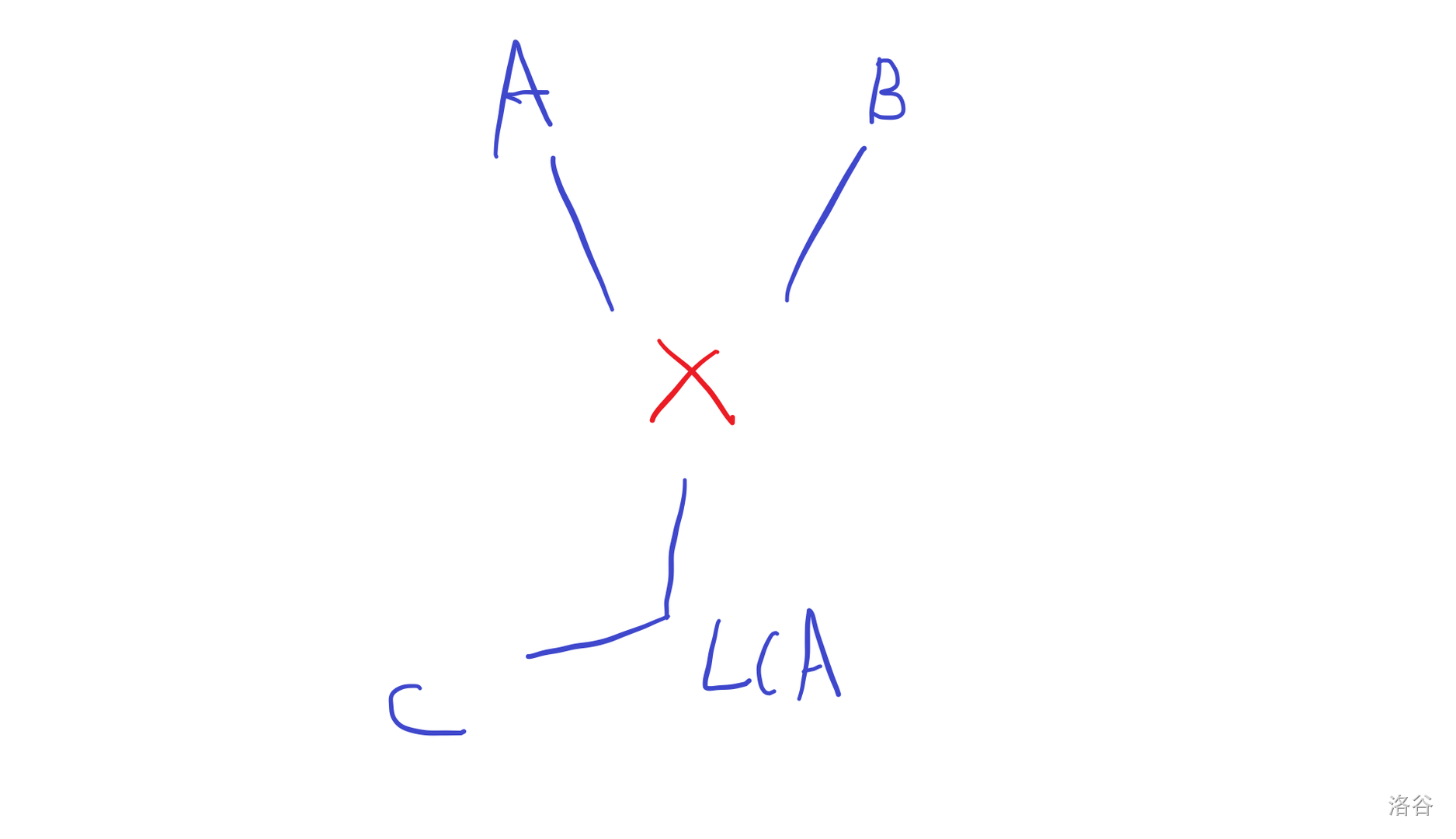
因为任意三点在树上的形态一定是这样：
所以 \(z\) 到 \(x,y\) 一定是先到了路径上，再分别去 \(x,y\)。（直接去 \(x\)，再从 \(x\) 去 \(y\) 也可以）
而从 \(z\) 去 \(x,y\) 路径上的部分是一样的，要长度相等，到路径上一定是到了中点。
证毕。
再看。
设 \(m\) 是 \(x,y\) 中点，\(LCA=lca(x,y)\)
- \(m\neq LCA\)
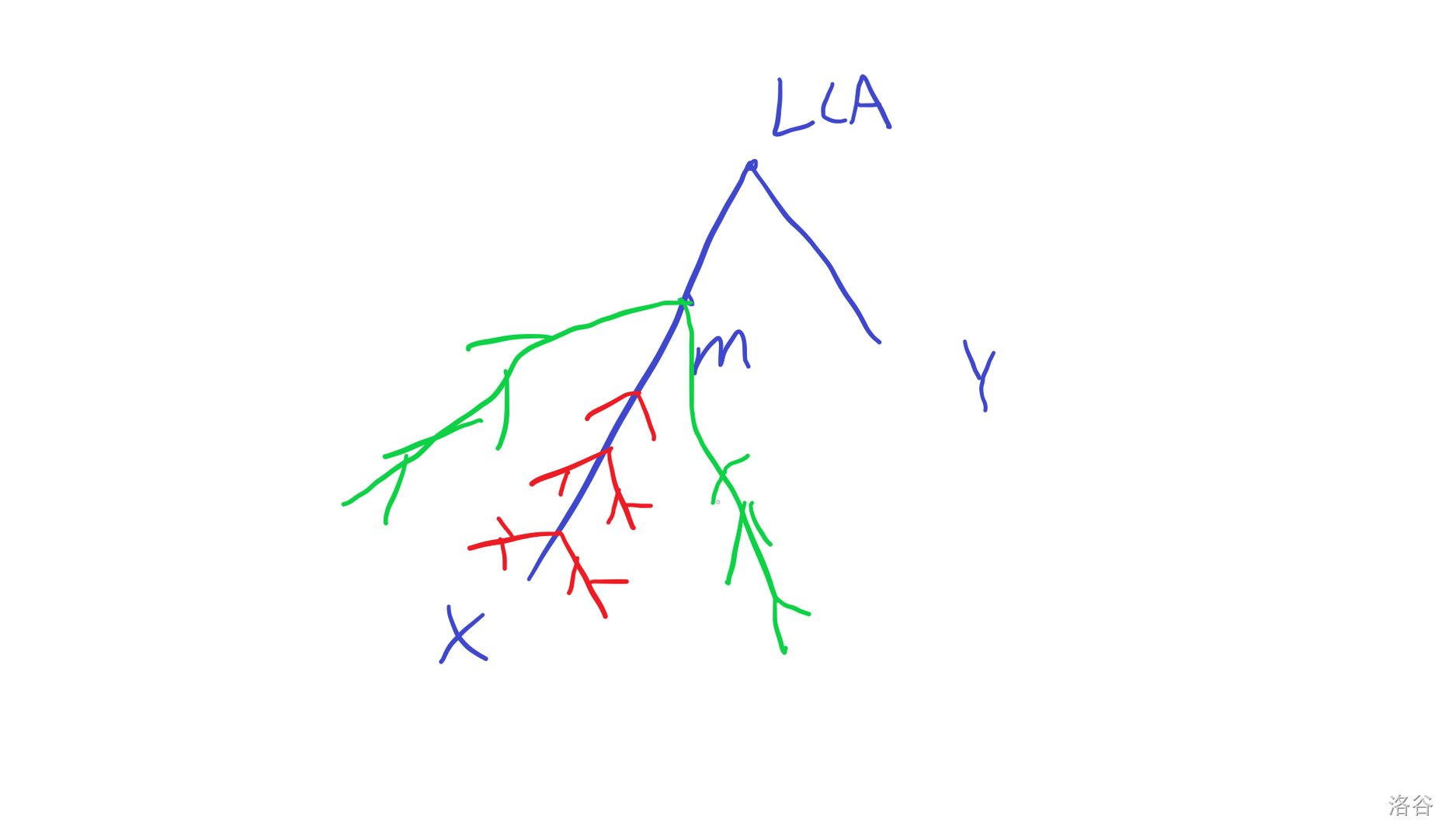
只有图中的绿色部分可以先到 \(m\)，再到 \(x,y\) 。
这些点的个数就是 \(sz[m]-sz[u]\)，\(u\) 是 \(m\) 向 \(x\) 方向的子结点。
- \(m=LCA\)
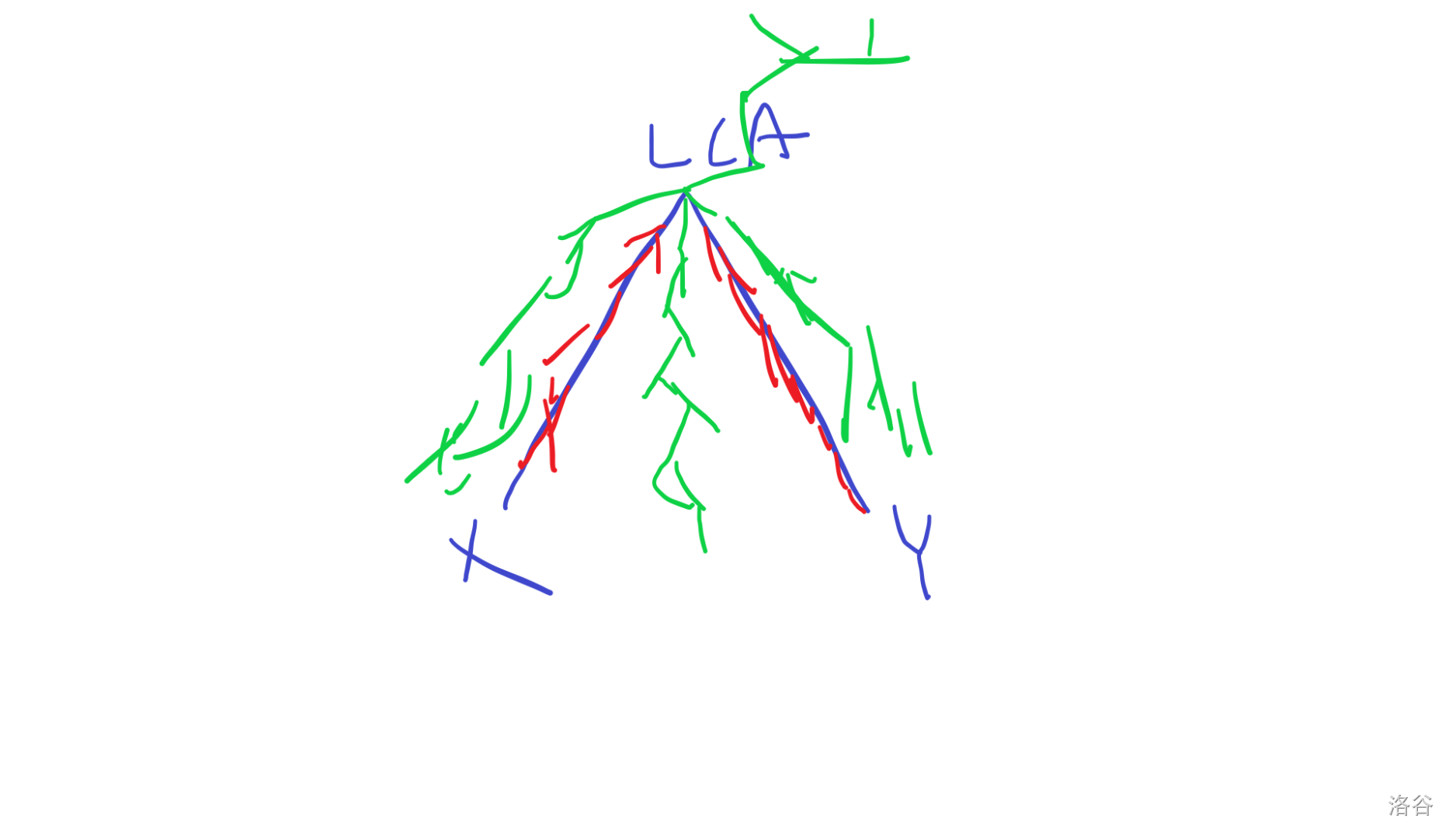
除了红色部分都可以（两个子结点的子树）。
个数就是 \(n-sz[u]-sz[v]\)，\(u,v\) 是两个子结点。
询问之前搜一遍，预处理 深度、倍增LCA等。
如果距离是奇数，没有点。
如果距离是偶数：
让深度较深的点往上走 \(dis/2\) 个，这个就是中点。
判断中点是不是 LCA，按上面分类讨论。
找对应的子结点用 \(anc()\) 函数即可。
紧急集合：
结论：三个点的LCA，到三个点的距离之和最小。
证明：
只需证明到其他点不会更好。
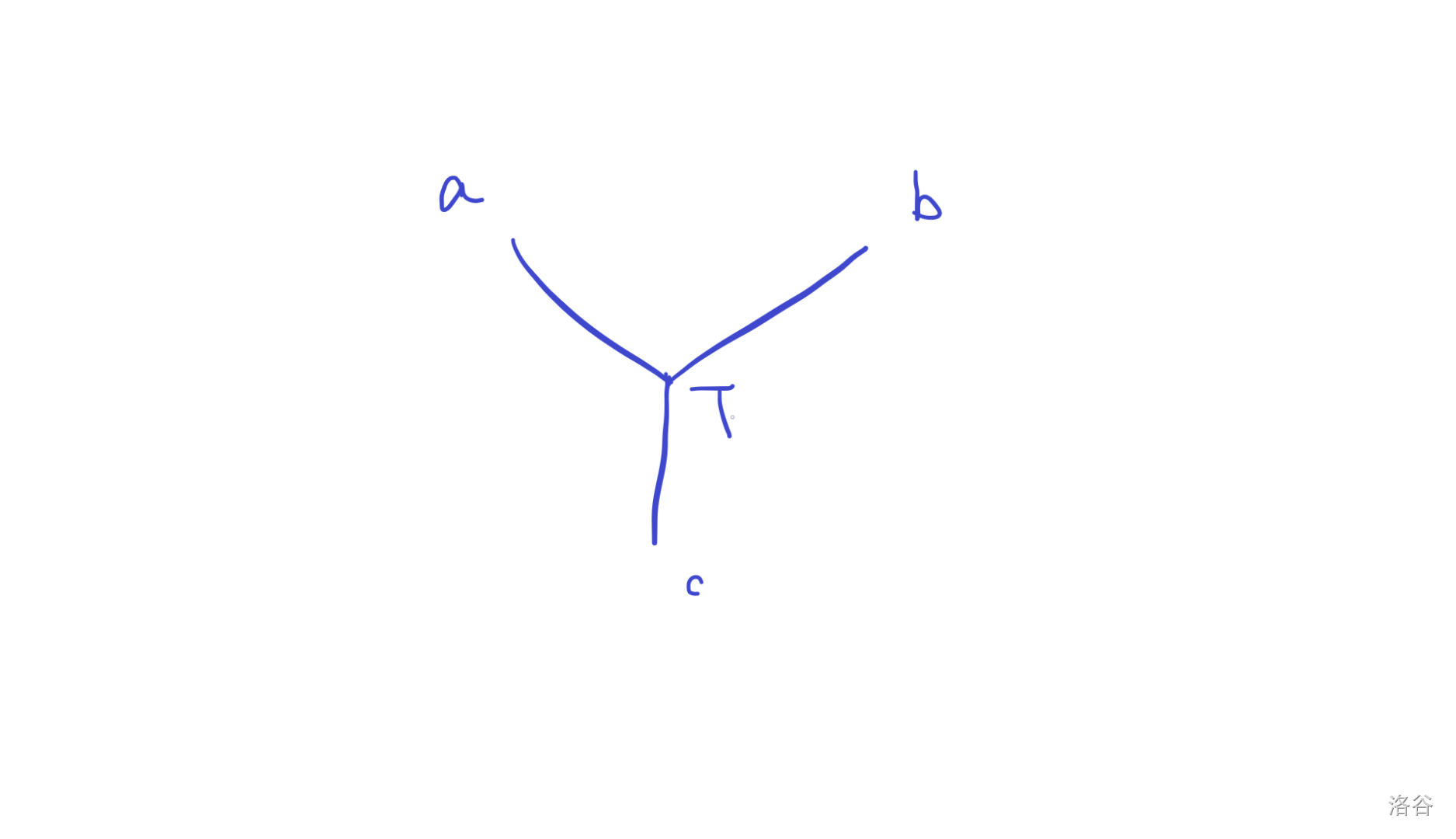
设 \(T\) 是三点 LCA 。
- 在 \(T\) 到三点的路径上的其他点
如果把这个点往 \(T\) 方向挪一个，总体距离会减少 1.
- 不在路径上的其他点
设这个点是 \(u\)，\(u\) 到 \(b,c\) 一定先到 \(b,c\) 路径上。
而从这个 \(b,c\) 路径上的点都比 \(T\) 远（上一类），\(u\) 一定比 \(T\) 更远。
综上，三点 LCA 到三个点的距离之和最小。
【题目分析】
火柴排队：
这是一道贪心题。
\(\sum\,(a_i-b_i)^2=\sum\,({a_i}^2+{b_i}^2-2a_ib_i)\)
而 \({a_i}^2+{b_i}^2\) 是固定的，所以我们为了使值最小，那么 \(a_ib_i\) 就要最大。
根据排序不等式，顺序和 \(\geq\) 乱序和 \(\geq\) 逆序和。
所以我们只需要把两列火柴从小到大排序即可。
先记录下编号，把两列火柴排序之后，把一列火柴的编号当作下标，另一列火柴的编号当作值，两个同样位置的火柴就构成元素。
求这些元素构成的数组的逆序对数即可。
这题下标关系有点乱，debug了10min。
Max Flow P，松鼠的新家：树上差分。
我们要给树上的一条路径上所有点加一个相同的权。
这条路径设为 \(u,v\)，记 \(LCA=lca(u,v)\)
我们只需要使 \(ans_u\)，\(ans_v\) 各加一，\(ans_{LCA}\)，\(ans_{fa[LCA]}\) 各减一即可。
最后一个结点的权，就是它子树里所有 \(ans\) 的和。
这样，我们相当于在树上做了一个差分。
\(ans_u\!+\!+\)，把根结点到 \(u\) 的都加了 1 .
\(ans_v\!+\!+\)，把根结点到 \(v\) 的都加了 1 .
\(ans_{LCA}\!-\!-\)，把根结点到 \(LCA\) 的都减了 1 .
\(ans_{fa[LCA]}\!-\!-\)，把根结点到 \(fa[LCA]\) 的都减了 1 .
这样我们看一下，从 \(u,v\) 到 \(LCA\) 的只被加了一个 1，没被减过。
\(LCA\) 加了两个 1，但是减了一个 1，抵消了。
从 \(fa[LCA]\) 到根结点，加了两个 1，也减了两个 1，抵消。
操作之后，再搜索一遍求子树和即可。
（注：本来还有两个 \(ans_0\!-\!-\)，但是因为 0 不在范围内就不写）
松鼠的新家还有一个坑点，不能直接把访问顺序连续两个看作路径
因为这样的话所有 既做过终点也做过起点的（2~n-1）就会多算。
所以最后还得循环减掉这多余的一个。
首先为了方便，给所有入度为 0 的点都添加一个父亲（太阳）。
接着，我们可以发现一件事情：
如果生物 \(a\) 会灭绝，等价于 \(a\) 所有的食物都会灭绝。
而 \(a\) 所有的食物都会灭绝，等价于这些食物的 \(LCA\) 会灭绝。
被捕食者的 vector 存储捕食者（食物链同向）。
把太阳设置为 0 。
拓扑排序，每删除一个点，就把所有捕食它的生物的入度减一。
还要更新所有捕食它的生物的食物 LCA。
如果入度为 0，加入队列，并把这个结点连向其食物LCA，食物 LCA 为父结点。，并更新这个结点的各层倍增LCA。
拓扑排序结束后，开始建二号图。
根据上面加粗的字体连的边，建成一棵树，0 号结点为根。
每个结点的 “灾难值” 就是这个点的子树规模 - 1.（不算自己）
\(dp[i]\) 表示当第 \(i\) 块积木归位时，前 \(i\) 块积木的最大归位数。
考虑 \(dp[i]\) 能由 \(dp[j]\) 转移的条件：
在 \(a[i]\) 能归位的情况下，\(a[j]\) 也能归位。
首先，\(a[i]\) 能归位，需要 \(a[i]\leq i\) 。
其次，\(a[j]\) 能归位，需要 \(a[j]\leq j\)，但因为我们把不可行赋值成 \(-\infty\)，所以不用理会。
再次，\(a[i] > a[j]\) 。
然后，\(a[j]\) 需要往下掉 \(j-a[j]\) 格，\(a[i]\) 也随之掉 \(j-a[j]\) 格，所以现在 \(a[i]\) 在 \(i-(j-a[j])=i-j+a[j]\) 格。
而 \(a[i]\) 要到 \(a[i]\) 处，所以 \(i-j+a[j]\ge a[i]\)，即 \(i-a[i]\geq j-a[j]\)。
所以：
\(i>j,a[i]-a[j]\leq i-j, i-a[i]\leq a[j]-j\)
而后两个条件可以推出第一个条件。
\(a[i]-a[j]\leq i-j, i-a[i]\leq a[j] - j\)
在 DP 之前把 \(a\) 按照 \(i - a[i]\) 排个序，可以再消除一个条件。
当然这就需要额外记录原来的编号，所以建议结构体。
\(dp[i]=max(dp[j]\;\,|\;\,a[i]>a[j])+1\)
所以来一个树状数组维护最大值，每次更新完就把 \(tr[i]\) 加上 \(dp[i]\) 。
更新时查询一下小于 \(a[i]\) 的最大值再加一。
题意简述：
给定一棵 \(n\) 个结点的带边权树和 \(m\) 条树上路径。
现在可以把一条边的边权改为 0 。
问：这 \(m\) 条路径上边权总和最大值最小是多少？
最大值最小，明摆着告诉你要二分。
那我们就二分，显然越小越好，越大越可行。
\(chk(mid)=true\) 表示最大值等于 \(mid\) 时可行。
现在我们的任务就变成了判断最大值是 \(mid\) 时可不可行。
最大值是 \(mid\) 可行，等价于：存在一条边删去之后，所有的路径的边权和都小于等于 \(mid\) 。
又等价于：存在一条边删去后，最长的边边权小于等于 \(mid\)，而且这条边是所有边权和大于 \(mid\) 的路径的公共边。
而一条边是公共边，就相当于这条边重复的次数就是路径条数。
这个东西可以用树上差分。
