ST表

【倍增算法】

先来介绍一些倍增。

倍增是用来加速枚举过程的算法。

一般可以把算法变成 $\log$ 级别 $O (n) => O (\log n)$ 。

举个栗子。

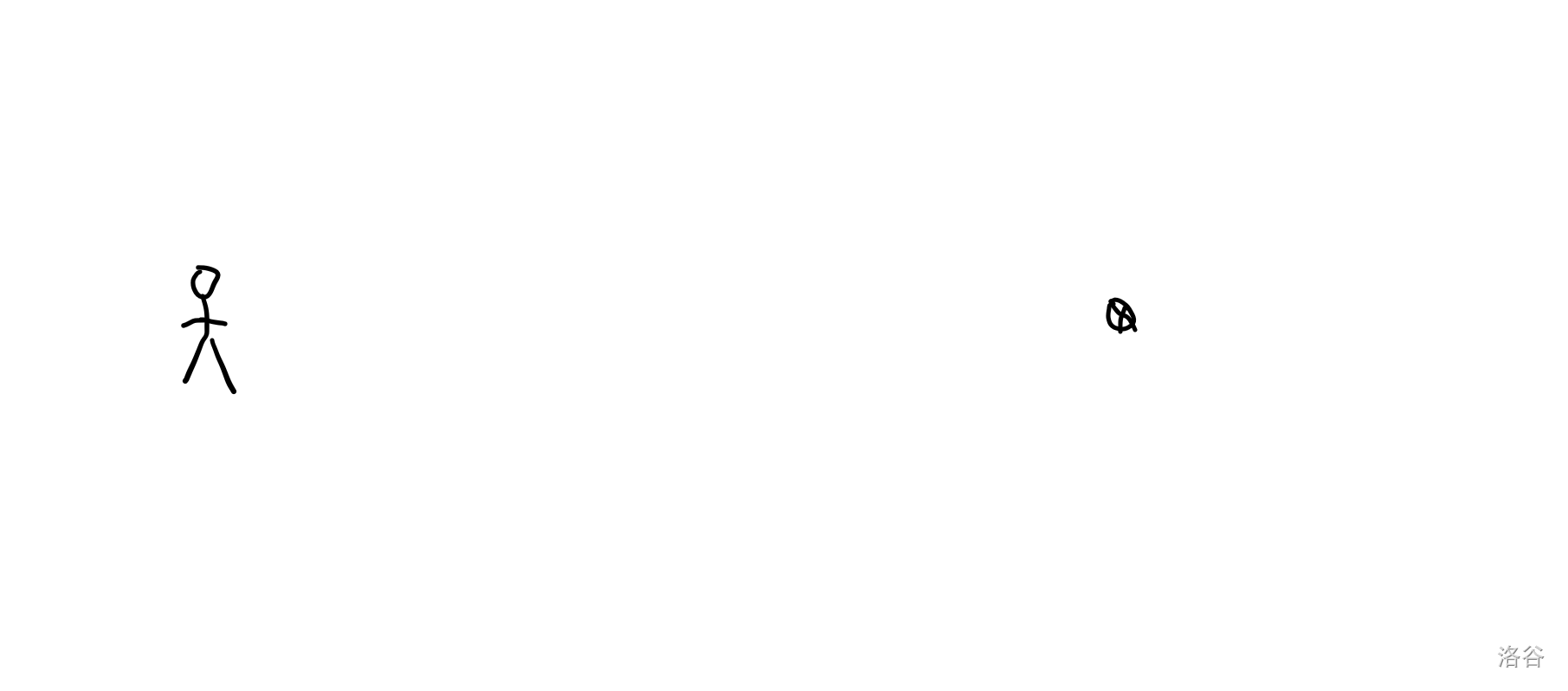
这里有一个小人，他想去右边的目标，但是他并不知道这个目标有多远。

不过他知道目前自己是在终点的左边还是右边。

我们说，他可以一步一步走，每走一步就看一下到了没，这当然可以走到终点。

但是这太慢了，所以我们要用第二种方法【倍增】。

我们让小人的步幅每次乘 2，于是小人就会这么走：

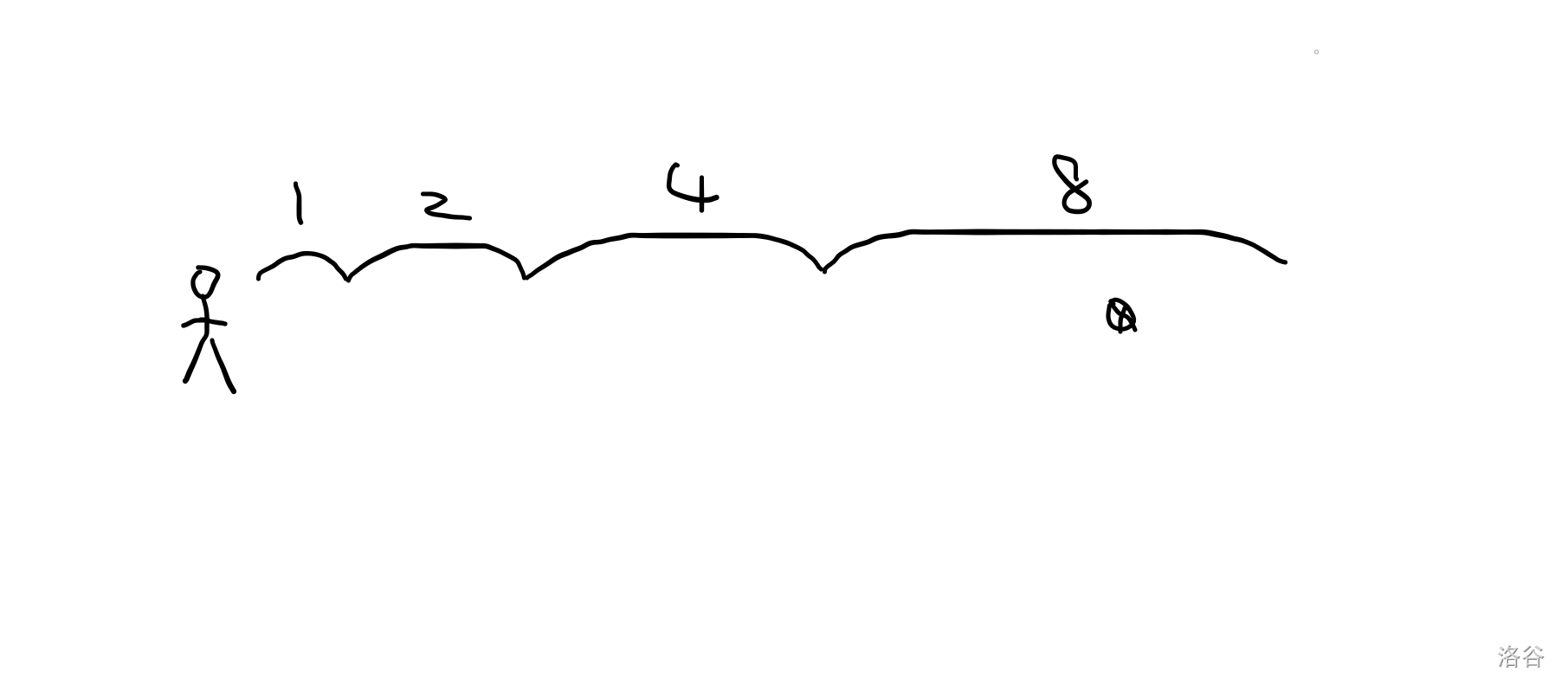
显然小人走超了。

但是，因为他是走了 8，所以他现在距离目标一定小于 8。

于是我们让他走 4。

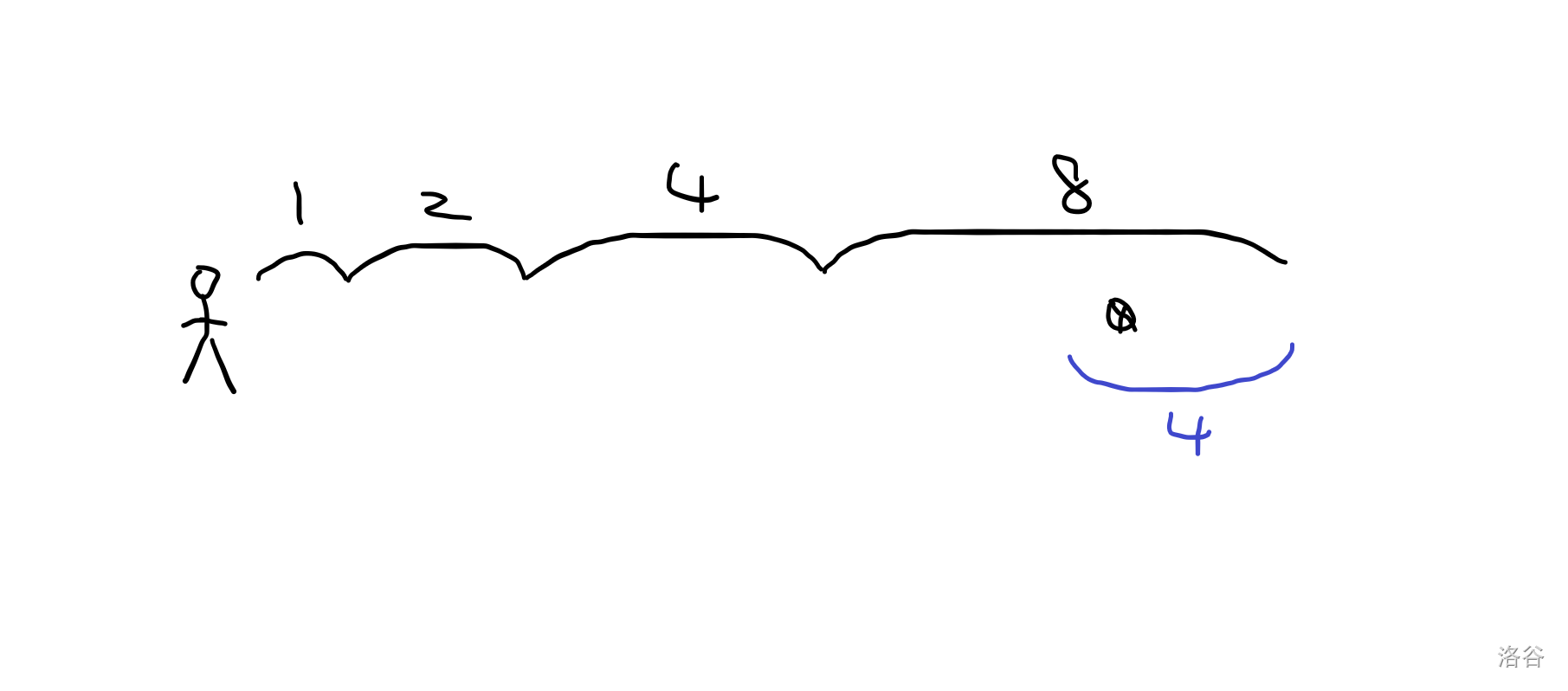
这一走又走过头了，但是同理，他现在距离目标小于 4 。

于是我们让他走 2 。

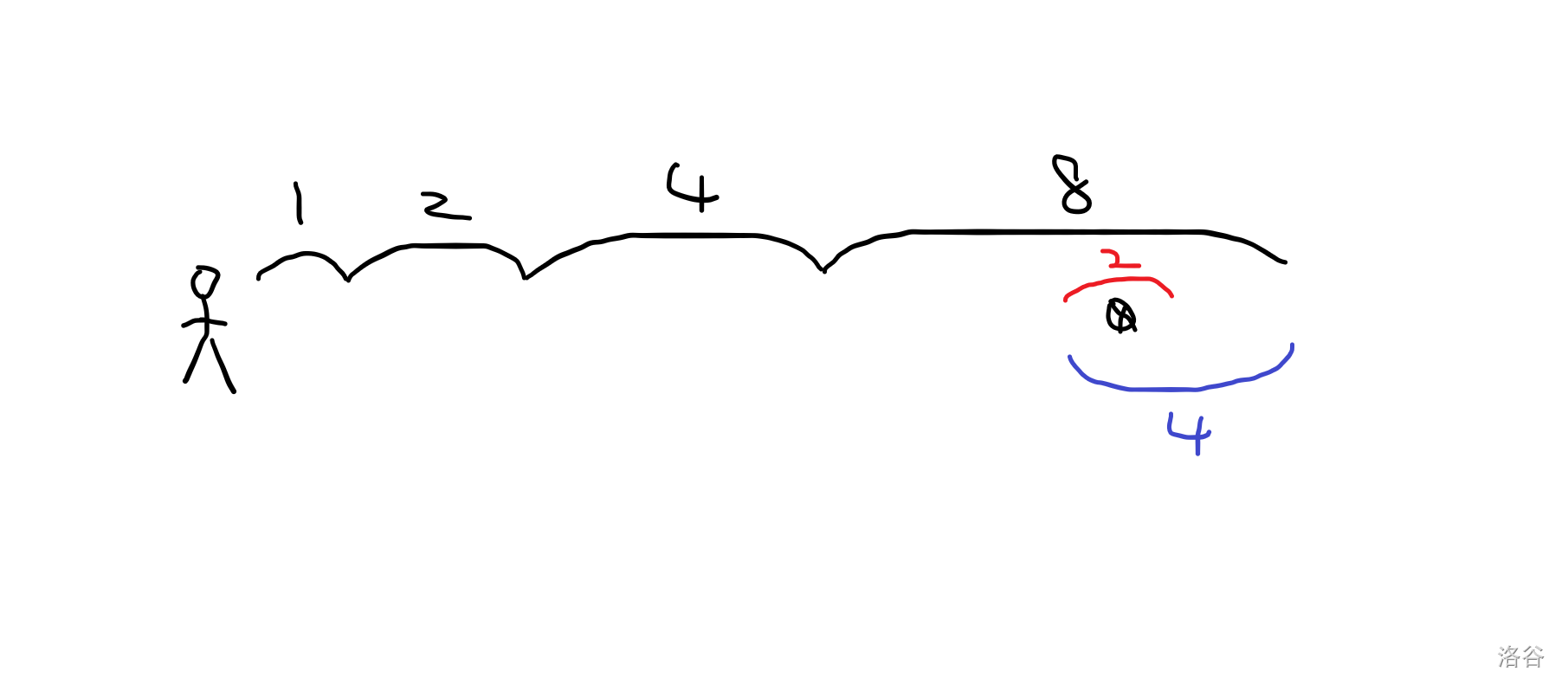
他又超了，但是距离目标小于 2 。

所以走 1。

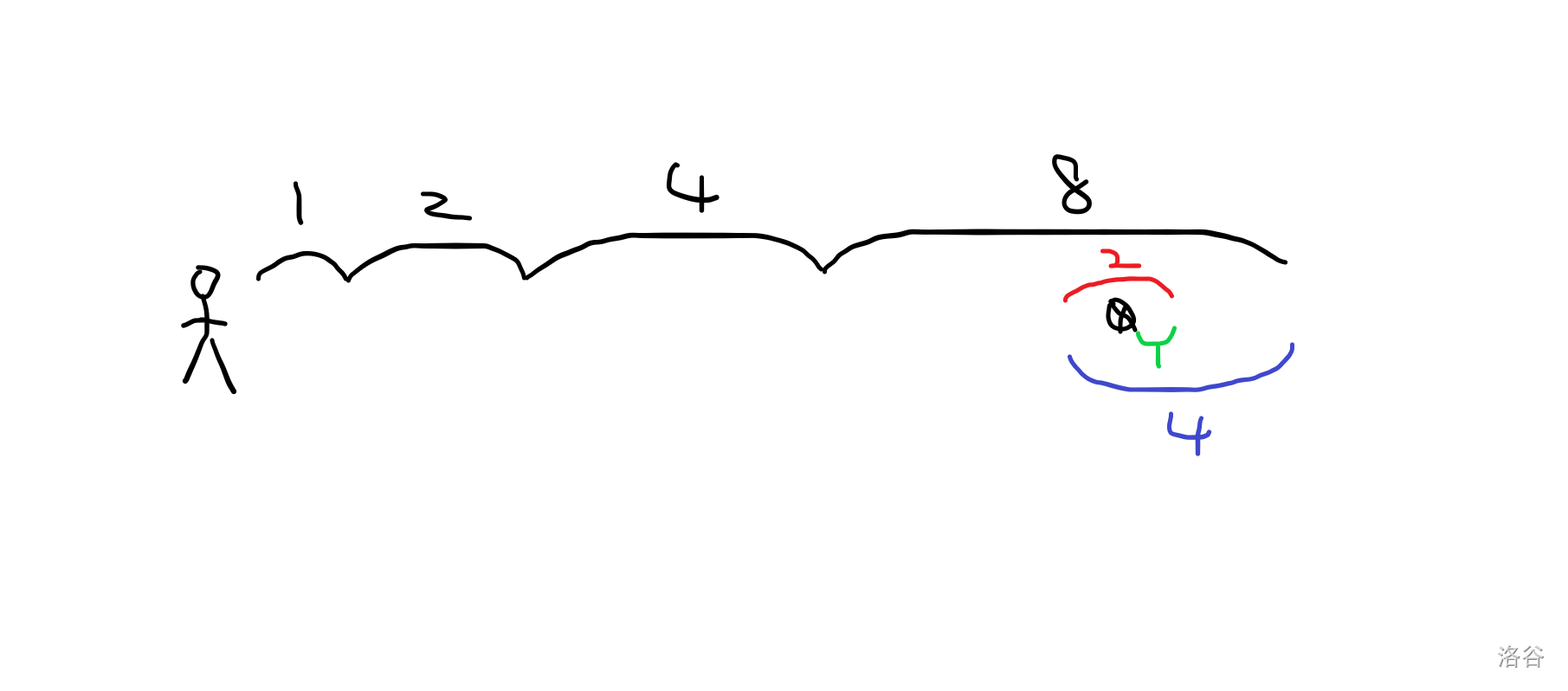
刚好到，整个过程是 $O (\log n)$ 的。

但是，我们需要多次判断是到了还是超了，还要倒回来，太麻烦。

于是，我们在代码实现时，会写一个 “倍减”。

换个栗子：

现在知道路程小于 32，我们就一定不会走一步 32 的。

考虑先走 16 。

我们判断一下，走了 16 之后还没到，所以可以走。

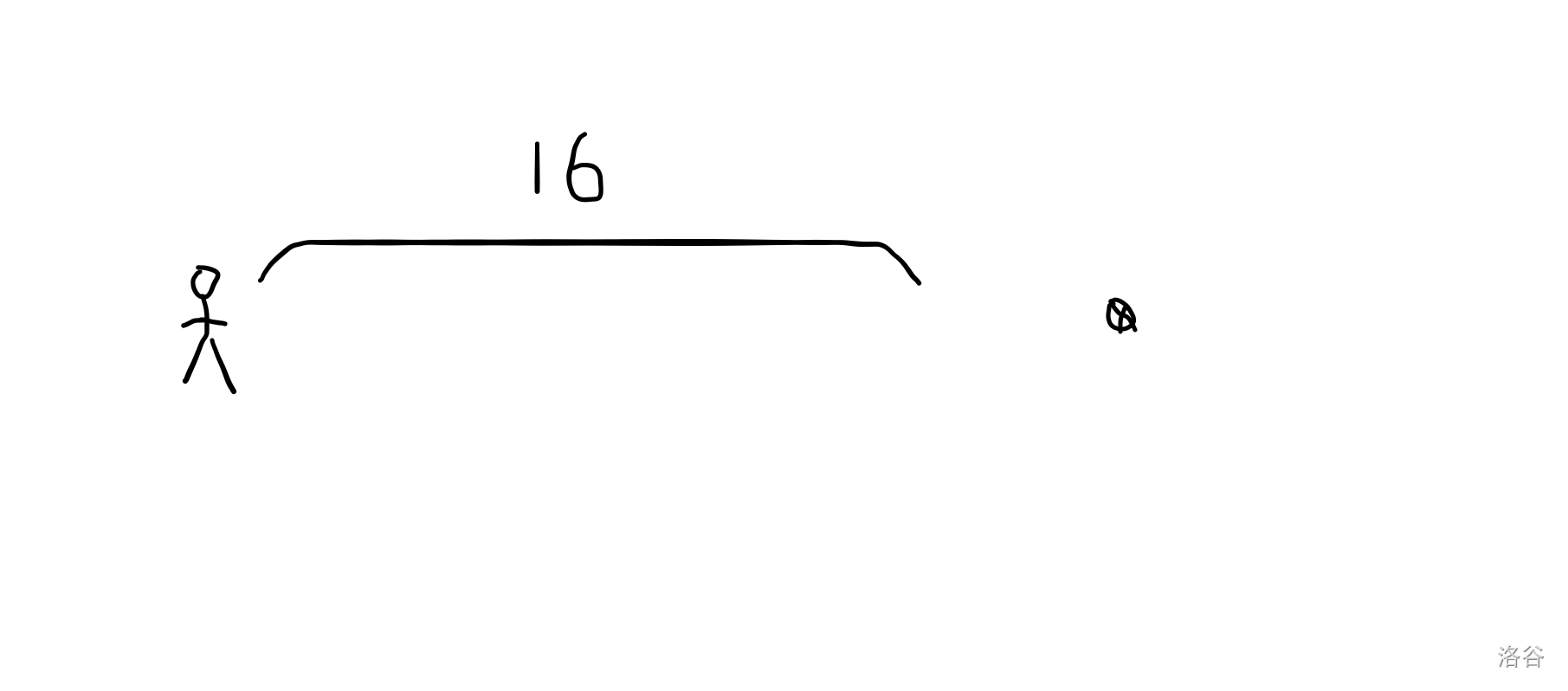
接着考虑走 8，但是我们一看，走 8 就超了，所以不走 8 。

接着考虑走 4，但是走 4 也超了，所以不走 4 。

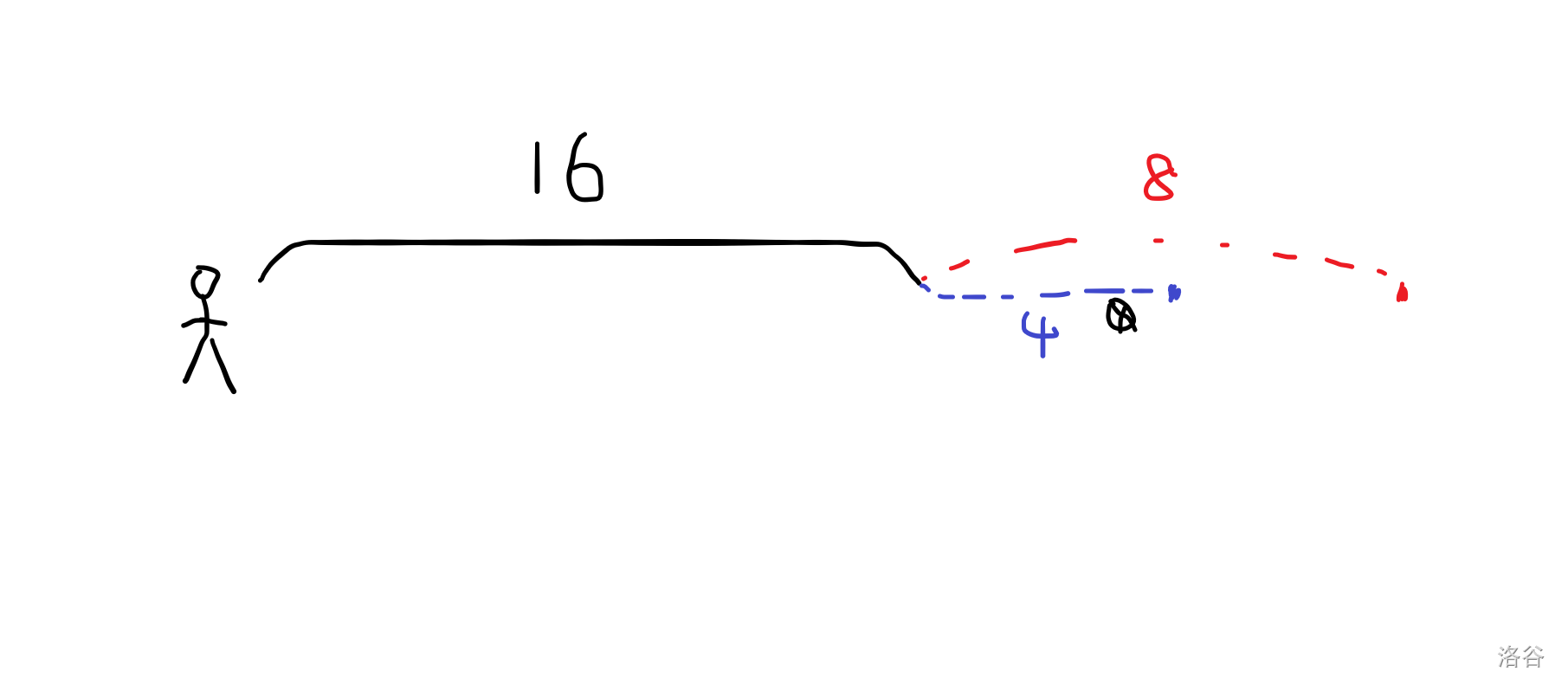
考虑走 2，发现不会超，于是走。

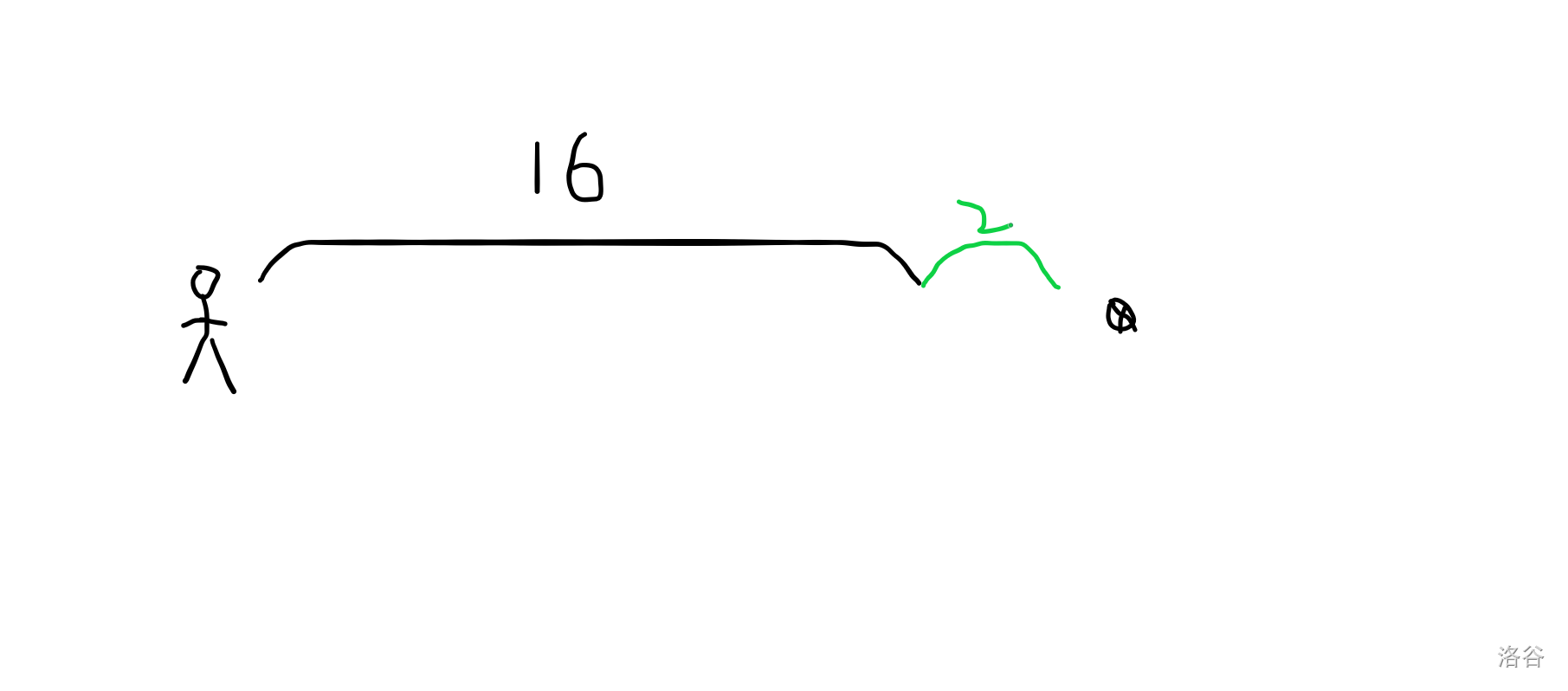
再走 1 。

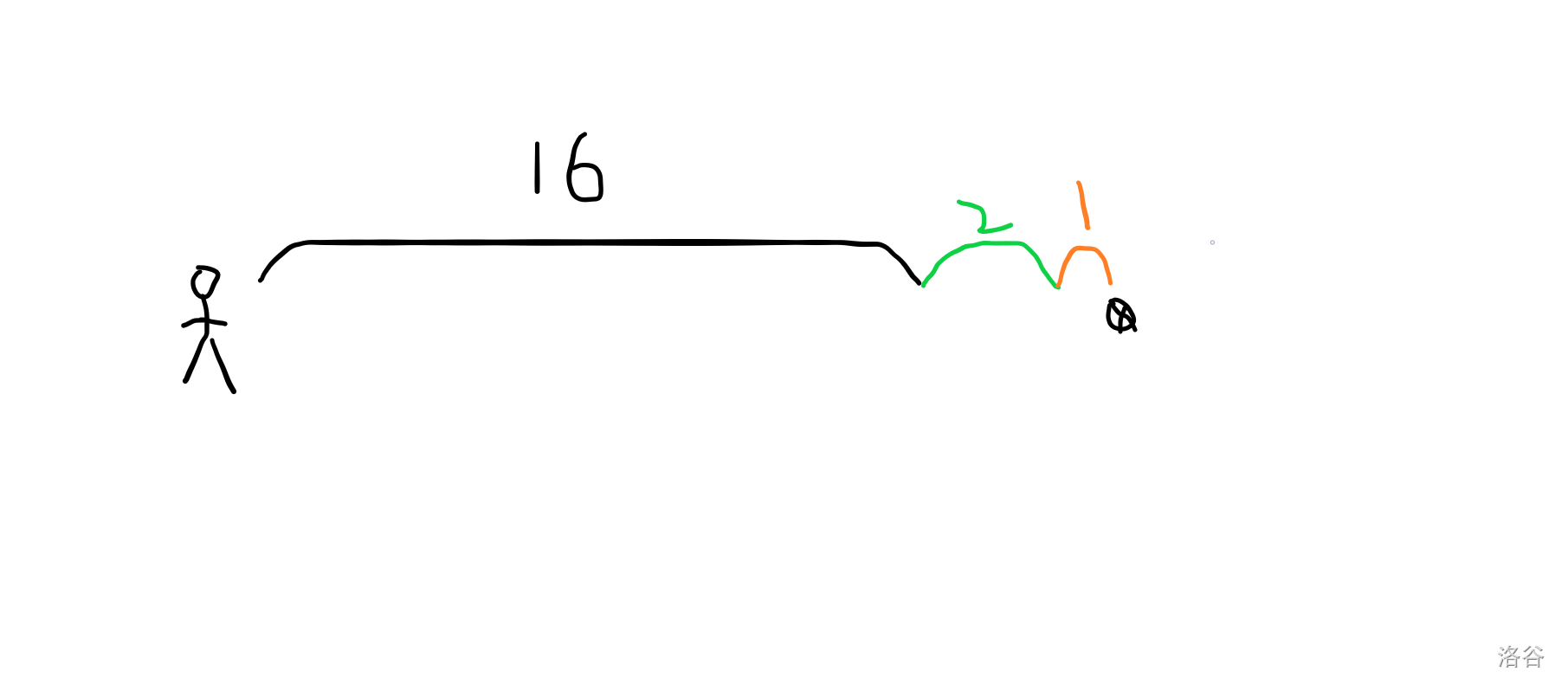
刚好到。

整个过程相当于把路程给二进制拆位了。

但是，我们可以知道，我们第一步设置的步幅一定要足够大，不然怎么走都走不到终点。

【倍增简单应用】

求 $\sqrt{n}$ 。

我们考虑定义 $a n s$ 和 $s t e p$ 。

初始 $a n s = 0$ ， $s t e p = n$ 。

不停循环，直到 $s t e p$ 达到所需精度。

每次循环判断 $a n s + s t e p$ 是否超过 $\sqrt{n}$ ，如果不超过就加上。

#include <cstdio>
using namespace std;


int main()
{
	int n = 10;
	scanf("%d", &n);
	//对步长step，每次折半 
	double ans = 0, step = n;
	while ((step /= 2) > 1e-10) //只要步长还不够小，就继续跳 
		if ((ans + step) * (ans + step) <= n) //如果跳了不到，则跳 
			ans += step;
	printf("%.10lf\n", ans); 
    return 0;
}

快速幂。

【倍增写法】

我们要求 $a^{b} m o d p$

考虑 $a^{1}, a^{2}, a^{4}, a^{8}, . . .$

把 $b$ 二进制拆位，把每一位 1 所对应的 $a$ 的幂乘进 $a n s$ 里。

【减治写法】

如果 $b \equiv 1 (\mod 2)$ ， $a^{b} = (a^{b / 2})^{2} \times a$ 。

否则 $a^{b} = (a^{b / 2})^{2}$ 。

递归即可。

#include <iostream>
using namespace std;

//倍增写法 
//long long fpow(long long a, long long b, long long p) { //a^b % p 
//	long long ans = 1, step = 1;
//	while (b > 0) {
//		if (b % (step * 2) != 0)
//			ans = (ans * a) % p, b -= step;
//		a = (a * a) % p, step *= 2;
//	}
//	return ans;
//} 

//减治写法 
long long fpow(long long a, long long b, long long p) { //a^b % p 
	if (b == 0)
		return 1;
	long long t = fpow(a, b / 2, p);
	return (b % 2 == 0) ? (t * t) % p : (t * t % p) * a % p;
} 
int main()
{
	long long a, b, p;
	cin >> a >> b >> p;
	cout << a << "^" << b << " mod " << p << "=" << fpow(a, b, p) << endl;
    return 0;
}

【RMQ问题和ST表】

RMQ：查询区间最值，ST 表专门处理这种问题。

【使用场景】

所需性质 “可结合性”。

“可加性” 就是两个区间的属性相加，就能求合起来的区间的属性。

“可结合性” 就是两个区间的属性可以做一个运算求合起来的区间的属性，而且不在乎两个区间是否重复。（比如 max，min，gcd）

优点：常数小，速度快，代码短。

缺点：只支持查询，不支持修改。

【实现】

记 $f [i] [j]$ 为 $i$ ~ $i + 2^{j} - 1$ 号元素中的最大值

初值： $f [i] [0] = a [i]$

转移： $f [i] [j] = m a x (f [i] [j - 1], f [i + 2^{j - 1}] [j - 1])$ （前一半和后一半）

查询：对于区间 $[l, r]$ ，其最值可以 $O (1)$ 地由 $f$ 数组推出

记 $l e n$ 为 $r - l + 1$ ， $\log_{2}^{l e n} = s$ ，则 $2^{s + 1} > l e n$

区间 $[l, r]$ 最大值 $= m a x (f [l] [s], f [r - 2^{s} + 1] [s])$

因为 $2 \times 2^{s} = 2^{s + 1} > r - l + 1$ ，所以两段必可完全覆盖

因为 max 有 “可结合性”，所以可以直接取 max。

预处理 $l o g$ 和 $p o w e r$ 的数组：

$p w_{i} = p w_{i - 1} \times 2$ ， $p w_{0} = 1$

$l g_{i} = l g_{[i / 2]} + 1$ ， $i$ 为大于 1 的正整数。

#include <cstdio>
#include <algorithm>
using namespace std;
//st[i][j]为2^i长度，j开始的区间（[j, j + 2^i - 1]）最值
int n, m, l, r, a[100005], pw[25] = {1};//pw[i]为2^i 
int st[20][100005];
//lg[i] 为 log_2 i下取整，即i长度区间需要两个lg[i]层的区间拼成 
int lg[100005] = {0}; 
void init() { //初始化st表与指数、对数表(pw, lg) 
	for (int j = 1; j <= n; j++) //第0层 
		st[0][j] = a[j];
	for (int i = 1; i <= 20; i++)
		pw[i] = pw[i - 1] * 2;
	for (int i = 2; i <= n; i++)
		lg[i] = lg[i / 2] + 1;
	for (int i = 1; pw[i] <= n; i++)//第i层，对应长度pw[i]，它应该小于n 
		for (int j = 1; j + pw[i] - 1 <= n; j++) //从j开始 
			st[i][j] = max(st[i - 1][j], st[i - 1][j + pw[i - 1]]);
} 

int qry(int l, int r) {//查询[l, r]最值 
	int i = lg[r - l + 1];//所需两个区间的层数  
	return max(st[i][l], st[i][r - pw[i] + 1]); 
}

int main()
{
	scanf("%d%d", &n, &m);
	for (int i = 1; i <= n; i++)
		scanf("%d", &a[i]);
	init();
	for (int i = 1; i <= m; i++) {
		scanf("%d%d", &l, &r);
		printf("%d\n", qry(l, r));
	}
    return 0;
}

【ST 表的一些扩展】

极差ST表，其实就是两个ST表，最大和最小；
二维ST表，大同小异， $s t_{i, x, y}$ 表示以 $(x, y)$ 为左上角，边长为 $2^{i}$ 的方阵的最值；
改变更新顺序的ST表， $s t_{i, j}$ 表示以 $j$ 结尾长度为 $2^{i}$ 的最值，这样每加入一个数都可以就地更新。

忠诚：一个字符都不用改的模板。

Frequent values：

把st表的每一个元素变成一个结构体，记录左端连续长度、右端连续长度、答案，更新照常更新，询问分为两块，然后看一下有没有重复部分。

索引和值、加加减减的比较容易混淆。

Strip：

动态规划， $d p_{i}$ 表示前 $i$ 个至少需要分成多少块。

初值：全部 inf，除了 $d p_{0} = 0$

递推：

$d p_{i} = d p_{p} + 1$ ， $p$ 是从小到大第一个满足条件的位置。

而且发现 $p$ 一定单调不降，所以只需要一个变量即可。

判断是否满足条件用st表加速。

答案： $d p_{n}$

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;
const int inf = 0x3f3f3f3f;

int n, s, l;
int a[100005];

int st1[25][100005];
int st2[25][100005];
int pw[25] = {1};
int lg[100005];

void init() {
	for (int i = 1; i <= 20; i++)
		pw[i] = pw[i - 1] * 2;
	for (int i = 2; i <= n; i++)
		lg[i] = lg[i / 2] + 1;
	
	for (int i = 1; i <= n; i++)
		st1[0][i] = st2[0][i] = a[i];
	for (int i = 1; pw[i] <= n; i++)
		for (int j = 1; j + pw[i] - 1 <= n; j++) {
			st1[i][j] = max(st1[i - 1][j], st1[i - 1][j + pw[i - 1]]);
			st2[i][j] = min(st2[i - 1][j], st2[i - 1][j + pw[i - 1]]);
		}
}

int qrymx(int l, int r) {
	int s = lg[r - l + 1];
	return max(st1[s][l], st1[s][r - pw[s] + 1]);
}

int qrymn(int l, int r) {
	int s = lg[r - l + 1];
	return min(st2[s][l], st2[s][r - pw[s] + 1]);
}

int qry(int l, int r) {
	return qrymx(l, r) - qrymn(l, r);
}

int dp[100005];
//前i个至少分成dp[i]份 

int main() {
	cin >> n >> s >> l;
	for (int i = 1; i <= n; i++)
		cin >> a[i];
	if (n < l) {
		cout << -1 << endl;
		return 0;
	}
	init();
	memset(dp, inf, sizeof dp);
	int p = 0;
	dp[0] = 0;
	for (int i = l; i <= n; i++) {
		while (i - p >= l && (qry(p + 1, i) > s || dp[p] == inf))
			p++;
		if (i - p >= l)
			dp[i] = min(dp[i], dp[p] + 1);
	}
	
//	for (int i = l; i <= n; i++)
//		cout << dp[i] << ' ';
	if (dp[n] == inf)
		cout << -1 << endl;
	else
		cout << dp[n] << endl;
	return 0;
}

Friends and Subsequences：

因为 $m a x$ 单调递增， $m i n$ 单调递减，所以在固定 $l$ 的时候，满足条件的 $r$ 一定是连续的，考虑二分。

二分出 $l l, r r$ ，分别代表最小的满足条件的右端点，和最大的满足条件的右端点，做差求和。

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;
const int N = 2e5 + 5;

int n, a[N] = {0}, b[N] = {0};
int st_mx[30][N]=  {0}, st_mn[30][N] = {{0}};
int pw[30] = {1}, logN[N];

void init() {
	for (int i = 2; i <= n; i++)
		logN[i] = logN[i / 2] + 1;
	for (int i = 1; i <= 20; i++)
		pw[i] = pw[i - 1] * 2;
	for (int i = 1; i <= n; i++)
		st_mn[0][i] = b[i], st_mx[0][i] = a[i];
	for (int i = 1; pw[i] <= n; i++)
		for (int j = 1; j + pw[i] - 1 <= n; j++) {
			st_mx[i][j] = max(st_mx[i - 1][j], st_mx[i - 1][j + pw[i - 1]]);
			st_mn[i][j] = min(st_mn[i - 1][j], st_mn[i - 1][j + pw[i - 1]]);
		}
}

int qry_mx(int l, int r) {
	int k = logN[r - l + 1];
	return max(st_mx[k][l], st_mx[k][r - pw[k] + 1]);
}

int qry_mn(int l, int r) {
	int k = logN[r - l + 1];
	return min(st_mn[k][l], st_mn[k][r - pw[k] + 1]);
}

int qry(int l, int r) {
	return qry_mx(l, r) - qry_mn(l, r);
}

int cal(int x) {
	int ll, rr;
	int l = x - 1, r = n; 
	while (r - l > 1) {
		int mid = (l + r) / 2;
		if (qry(x, mid) >= 0)
			r = mid;
		else
			l = mid; 
	}
	ll = r;
	
	l = x, r = n + 1;
	while (r - l > 1) {
		int mid = (l + r) / 2;
		if (qry(x, mid) > 0)
			r = mid;
		else
			l = mid; 
	}
	rr = l;
	
	if (qry(x, ll) == 0 && qry(x, rr) == 0)
		return rr - ll + 1;
	return 0;
}

int main() {
	cin >> n; 
	for (int i = 1; i <= n; i++)
		cin >> a[i];
	for (int i = 1; i <= n; i++)
		cin >> b[i];
	init();
	long long ans = 0;
	for (int i = 1; i <= n; i++)
		ans += cal(i);
	cout << ans << endl;
	return 0;
}

posted @ 2024-02-05 14:31 FLY_lai 阅读(30) 评论(0) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

相关博文：

· 倍增 LCA

· 单调性优化

· 倍增 ST表

· 算法笔记——ST表

· 倍增算法学习指南

阅读排行：
· 阿里最新开源QwQ-32B，效果媲美deepseek-r1满血版，部署成本又又又降低了！
· 单线程的Redis速度为什么快？
· SQL Server 2025 AI相关能力初探
· AI编程工具终极对决：字节Trae VS Cursor，谁才是开发者新宠？
· 展开说说关于C#中ORM框架的用法！

公告

昵称： FLY_lai
园龄： 1年1个月
粉丝： 9
关注： 10

+加关注

2025年3月

日

一

二

三

四

五

六

FLYlai

ST表

【倍增算法】

【倍增简单应用】

【倍增写法】

【减治写法】

【RMQ问题和ST表】

【使用场景】

【实现】

【ST 表的一些扩展】

公告

搜索

常用链接

我的标签

合集

随笔分类

随笔档案

阅读排行榜

评论排行榜

推荐排行榜

最新评论