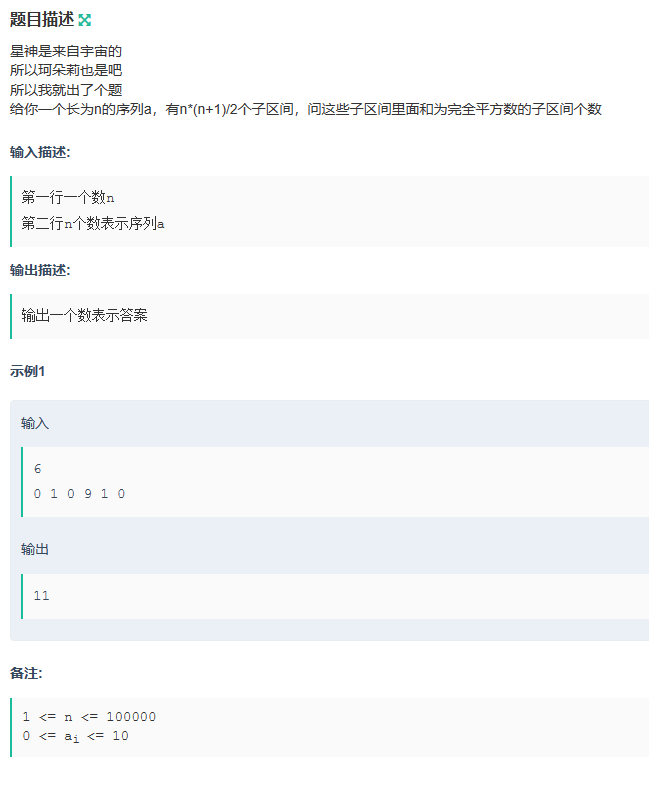
珂朵莉与宇宙

#include<bits/stdc++.h>
const int N = 1e6 + 10;
int Cnt[N], S[N];//Cnt用于记录前缀和出现的次数 S用于计算前缀和
using namespace std;

int main()
{
int n, x = 0;
long long ans = 0;//记录最终答案

Cnt[0] = 1;//第一个数初始化
// 因为前缀和为0也是一种完全平方数
scanf("%d", &n);

for(int i = 1; i <= n; i++ ){
scanf("%d", &x);
S[i] = S[i - 1] + x; //预处理前缀和

for(int j = 0; j * j <= S[i]; j++ )//从0到当前前缀和枚举完全平方数
ans += Cnt[S[i] - j * j];
Cnt[S[i]] ++;// 更新前缀和出现的次数
}

printf("%lld\n", ans);
return 0;
}

 

在一个长为n的序列里找子区间个数关于和为完全平方数

而枚举的对象是子区间的和，自然就可联想到前缀和的知识点来解决，可以找到任意一段区间的前缀和

计算l到r的和的公式为 S[r] - S[l - 1]

要他的和为完全平方数 即 有一个数num满足 S[r] - S[l - 1] = num * num

移一下就变成了 S[r] - num * num = S[l - 1]

对于每个 j从0开始枚举到sqrt(S[i]), 如果S[i] - j方的前缀和出现过，那么就存在一个子区间的和为S[i]

最后更新cnt[S[i]] 表示当前前缀和出现了一次  最终答案存储在ans中 输出既可