算法笔记之并查集

一、并查集的定义

并查集是一种树型的数据结构，用于处理一些不相交集合（disjoint sets）的合并及查询问题。常常在使用中以森林来表示。

并查集，顾名思义，支持以下两种操作操作：

• 并(Union)：把两个不相交的集合合并为一个集合。

• 查(Find)：查询两个元素是否在同一个集合中。

二、并查集的实现

并查集往往用树来存，使用 \(f\) 数组表示每个节点的父节点，初始 \(f_i=i\)，即认自己为父亲，

那么我们就可以得到这样的一颗树：

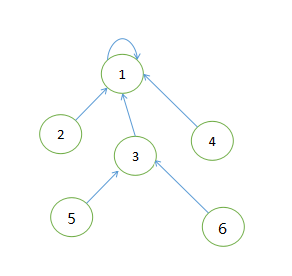
查询

查询 \(x\) 的根节点就是找到其祖先。

int f[N];
int find(int x)
{
	if(f[x]==x)return x;
	return find(f[x]);
}

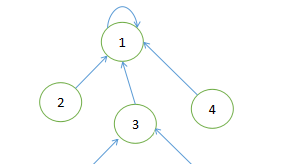
但这样会有一个问题：当数据很大时，树的深度会很高，所以我们需要压缩路径。

我们可以在查询的过程中，让 \(x\) 认自己的祖先为父亲，那么就可以大大缩小深度。

优化代码如下：

int f[N];
int find(int x)
{
	if(f[x]==x)return x;
	return f[x]=find(f[x]);
}

\[这个人颓废去了，n年后再更 \]