线性回归

线性回归(Linear regression)是利用回归方程(函数)对一个或多个自变量(特征值)和因变量(目标值)之间关系进行建模的一种分析方式。

特点：只有一个自变量的情况称为单变量回归，大于一个自变量情况的叫做多元回归

通用公式：h(w) = w₁x₁+w₂x₂+w₃x₃+...+b=w^Tx + b

其中w，x可以理解为矩阵：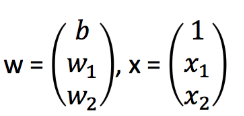 

线性回归当中的关系有两种，一种是线性关系（单特征与目标值的关系呈直线关系，或者两个特征与目标值呈现平面的关系），另一种是非线性关。

线性回归损失函数定义为：

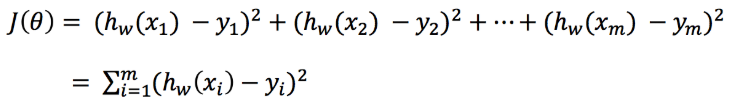
• y_i为第i个训练样本的真实值
• h(x_i)为第i个训练样本特征值组合预测函数
• 又称最小二乘法

 

线性回归经常使用的两种优化算法：

1. 正规方程

理解：X为特征值矩阵，y为目标值矩阵。直接求到最好的结果

缺点：当特征过多过复杂时，求解速度太慢并且得不到结果

 

2. 梯度下降(Gradient Descent)

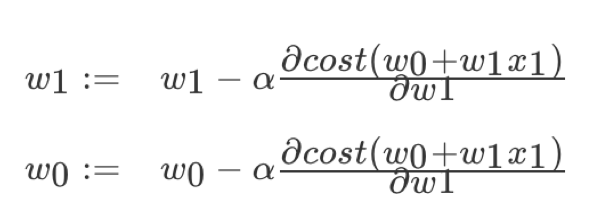
理解：α为学习速率，需要手动指定（超参数），α旁边的整体表示方向，沿着这个函数下降的方向找，最后就能找到山谷的最低点，然后更新W值

使用：面对训练数据规模十分庞大的任务 ，能够找到较好的结果

 

sklearn提供的线性回归API

sklearn.linear_model.LinearRegression(fit_intercept=True)

通过正规方程优化
fit_intercept：是否计算偏置
LinearRegression.coef_：回归系数
LinearRegression.intercept_：偏置
sklearn.linear_model.SGDRegressor(loss="squared_loss", fit_intercept=True, learning_rate ='invscaling', eta0=0.01)

通过使用SGD优化
loss:损失类型 *
fit_intercept：是否计算偏置
learning_rate : string, optional

学习率填充
'constant': eta = eta0
'optimal': eta = 1.0 / (alpha * (t + t0)) [default]
'invscaling': eta = eta0 / pow(t, power_t)
power_t=0.25:存在父类当中
SGDRegressor.coef_：回归系数
SGDRegressor.intercept_：偏置

 

示例： 波士顿房价预测

数据集来源：UCI datasets 

 

 

分析
回归当中的数据大小不一致，会导致结果影响较大，所以需要做标准化处理，同时对目标值也需要做标准化处理。
1. 数据分割与标准化处理
2. 回归预测
3. 线性回归的算法效果评估

 

回归性能评估

均方误差(Mean Squared Error)MSE)评价机制：

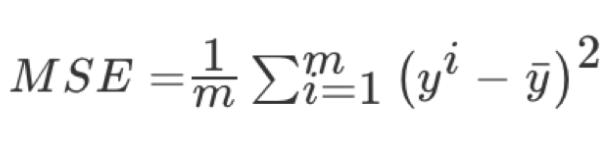
yⁱ为预测值，¯y为真实值

 

回归性能评估的sklearn API：

sklearn.metrics.mean_squared_error(y_true, y_pred)
均方误差回归损失
y_true:真实值
y_pred:预测值
return:浮点数结果

 

完整代码：

?

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58

from sklearn.model_selection import train_test_split from sklearn.metrics import mean_squared_error from sklearn.linear_model import (     LinearRegression,     SGDRegressor ) from sklearn.preprocessing import StandardScaler from sklearn.datasets import load_boston     def mylinearregression():     """     线性回归预测房价     :return:     """     lb = load_boston()       # 对数据集进行划分     x_train, x_test, y_train, y_test = train_test_split(         lb.data, lb.target, test_size=0.3, random_state=24     )       # 需要做标准化处理对于特征值处理     std_x = StandardScaler()       x_train = std_x.fit_transform(x_train)     x_test = std_x.fit_transform(x_test)       # 对于目标值进行标准化     std_y = StandardScaler()       y_train = std_y.fit_transform(y_train.reshape(-1, 1))     y_test = std_y.transform(y_test.reshape(-1, 1))       y_test = std_y.inverse_transform(y_test)       # 使用线性模型进行预测 使用正规方程求解     lr = LinearRegression()     lr.fit(x_train, y_train)       y_lr_predict = std_y.inverse_transform(lr.predict(x_test))       print("正规方程预测的结果为：", y_lr_predict)     print("正规方程的均方误差为：", mean_squared_error(y_test, y_lr_predict))       # 梯度下降进行预测     sgd = SGDRegressor()     sgd.fit(x_train, y_train)     print("SGD的权重参数为：", sgd.coef_)       y_sgd_predict = std_y.inverse_transform(sgd.predict(x_test))     print("SGD的预测的结果为：", y_sgd_predict)     print("SGD的均方误差为：", mean_squared_error(y_test, y_sgd_predict))       return None     mylinearregression()

 

执行结果

 

 梯度下降预测方法：

?

1 2 3 4 5 6 7 8 9

SGDRegressor()   def __init__(self, loss="squared_loss", penalty="l2", alpha=0.0001,                  l1_ratio=0.15, fit_intercept=True, max_iter=None, tol=None,                  shuffle=True, verbose=0, epsilon=DEFAULT_EPSILON,                  random_state=None, learning_rate="invscaling", eta0=0.01,                  power_t=0.25, early_stopping=False, validation_fraction=0.1,                  n_iter_no_change=5, warm_start=False, average=False,                  n_iter=None):

通过调参，可以找到学习率效果更好的值

 

线性回归的两种优化方法对比：

梯度下降	正规方程
需要选择学习率	不需要
需要迭代求解	一次运算得出
特征数量较大可以使用	需要计算方程，时间复杂度高O(n3)

 适用范围：

• 小规模数据：
  • LinearRegression(不能解决拟合问题)
  • 岭回归
• 大规模数据：SGDRegressor