数据结构
线段树
维护的信息需要满足结合律。
懒标记维护的信息还需要满足交换律。
如果我们要维护多种类的修改标记呢,比如 乘法和加法。直观反应是某个运算标记遇到另一个就直接下传,但是其实这个行不通,万一下传之后又遇到另一个标记了,那岂不是要一直下传了,复杂度就不对了。只需要考虑 \(\times\) 遇到了更早的 \(+\),和 \(+\) 遇到了更早的 \(\times\)。考虑乘法对于加法有分配律,我们直接在 \(\times x\) 遇到 \(+y\) 的时候,改为 \(+(x\times y)\),遇到加法直接加在加法标记上,然后下传的时候先乘后加即可。
历史信息
区间加,区间赋值,区间历史最大值。
步骤分为信息设计,标记设计,和标记合并。
- 信息设计
我们维护 \(mx\) 和 \(h\) 分别表示区间最大值和区间历史最大值。
信息合并就是直接从左右儿子取 \(\max\) 即可。
- 标记设计
对于维护 \(mx\),我们需要设计 \(ad,as\) 分别表示增加的值和赋值的值。
考虑两个标记的共存问题,可以发现有 \(ad\) 的时候可以更新 \(as\) 并清空 \(ad\),有 \(as\) 的时候更新 \(ad\) 的话直接 \(as\gets ad\) 即可。
更新的时候如果有 \(as\),那么 \(mx\gets as\),否则 \(mx\gets mx+ad\)。
对于维护 \(hs\),我们需要设计 \(h_{ad},h_{as}\),表示第一次赋值操作之前的历史最大前缀和和历史最大赋值(可以发现第一次赋值操作之后,此后的加法操作都变成了赋值操作)。
更新的时候直接 \(h\gets \max(h,h_{as},mx+h_{ad})\)。
- 标记合并
现在需要处理标记下传之后相遇的情景。
我们设 \(l\) 是先打上的标记,\(r\) 是后打上的标记。
可以发现之前说过分水岭是是否有过 \(as\) 标记,所以我们直接对于 \(4\) 种情况讨论是否有 \(as\) 标记即可。
都没有 \(as\) 标记,
只有 \(l\) 有 \(as\) 标记,此时 \(ad\) 直接设为 \(0\) 即可。
只有 \(r\) 有 \(as\) 标记,此时 \(ad\) 直接设为 \(0\) 即可。
\(l,r\) 都有 \(as\) 标记,此时 \(ad\) 直接设为 \(0\) 即可。
历史和
比历史信息好写啊。就是我们维护当前区间和 \(s\),历史和 \(hs\) 还有区间长度 \(len\),然后维护标记 \(ad,had\) 表示加法标记,历史和加法标记。一个在 \(T_1\) 版本加入的信息 \(v\),在 \(T_2\) 版本的贡献就是 \((T_2-T_1)\times v\),因此对于 \(h\) 类信息的更新一律要乘以当前版本 \(T_i\),最后答案就是 \(T\times s-h_s\)。
一些思考
本质就是设计要维护的信息 Info 和对应维护信息的标记 Tag,然后有三个合并,左右儿子合并 Info+Info,标记更新 Info+Tag,下传标记 Tag+Tag
CF1677E. Tokitsukaze and Beautiful Subsegments
定义一个区间 \([l,r]\) 是好的,当且仅当存在 \((i,j)\),满足 \(l\le i<j\le r\) 且 \(p_i\times p_j=\max\limits_{k=l}^rp_k\)。给定 \(q\) 次询问,每次给出 \([l_i,r_i]\),求其中有多少个好的子区间。\(n\le 10^5,q\le 2\times 10^5\)。
自己想出来了,很有成就感。
尝试找到可以贡献的区间放到二维平面内,其中横坐标代表左端点,纵坐标代表右端点,然后求子区间就是平面矩阵求和。
对于 \(p_i\times p_j\) 是一个经典的调和级数处理,我们枚举 \(p_i\),再枚举 \(p_j\) 满足 \(p_i\times p_j\le n\),是 \(O(n\operatorname{ln} n)\)。此时确定了 \(i,j\) 之后可以唯一确定 \(k\),接着根据三者位置关系可以得到若干满足条件的区间。
可以用单调栈求出 \(p_k\) 作为最大值的区间 \([ml_k,mr_k]\),如果 \(i,j\in [ml_k,mr_k]\) 的话,我们就可以得到左端点在 \([ml_k,\min(i,j,k)]\) 之间,右端点在 \([\max(i,j,k),mr_k]\) 之间的区间可以对于答案产生贡献。
对于一个 \(k\) 可能有多个贡献区间,某些贡献会算重。考虑去重,对于 \(k\) 所支配的若干个区间 \((l_i,r_i)\),我们以 \(l_i\) 为第一关键字降序排序,\(r_i\) 为第二关键字升序排序。考虑 \((l_{i-1},r_{i-1})\) (棕线) 和 \((l_i,r_i)\) (银线),可以发现银线中去除棕线内容后就是红色部分,于是我们每次截取这个红色部分矩阵加入贡献即可。
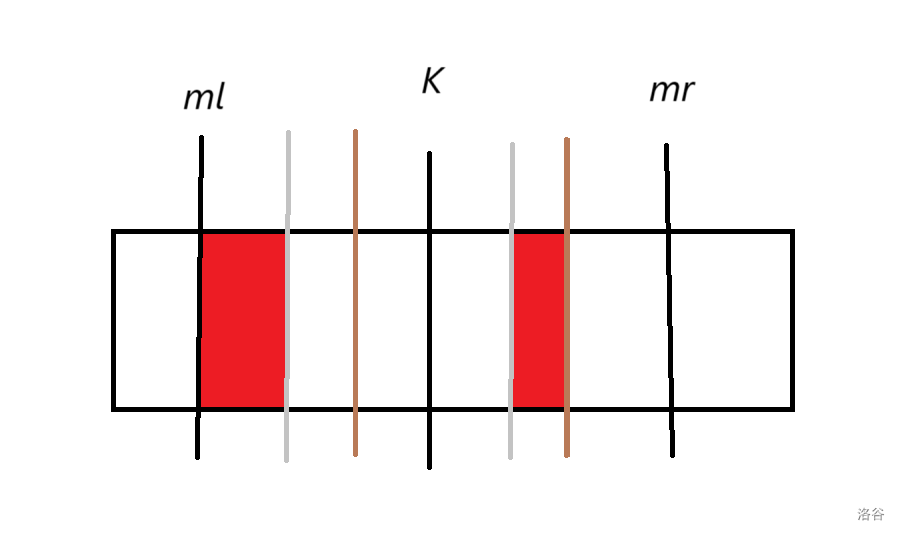
这样子就不会算重了,问题就变成了若干次矩阵加之后进行若干次矩阵求和,可以用扫描线加历史和来解决。
时间复杂度 \(O(n\log^2 n)\)。贡献区间个数是 \(O(n\operatorname{ln} n)\) 级别的,所以是 2log。
P8868 [NOIP2022] 比赛
记区间 \([l,r]\) 的答案为 \(g(l,r)\)。
考虑扫描线去扫右端点 \(R\),我们同时维护左端点的答案 \(f_L\) 表示对于满足 \(L\le i \le R\) 的右端点 \(i\) 的答案之和,也就是 \(f(L)=\sum\limits_{i=L}^Rg(L,i)\)。那么在扫到 \(R\) 的时候,对于询问 \([x,R]\),答案就是 \(\sum\limits_{i=L}^R f(i)\)。可以发现每次将 \(R\to R+1\) 的时候,对于每个 \(f(L)\),新增的区间都是 \([L,R+1]\),可以暴力从后往前扫一遍得到每个 \([i,R+1]\) 的 \(a,b\) 最大值更新答案。这样子维护的时间复杂度是 \(O(n^2+nq)\),如果改用线段树直接维护 \(f\) 的话可以做到 \(O(n^2+q\log n)\),但是 \(n^2\) 的瓶颈导致拿不到更多的分。
每次新加入一个数影响了一段后缀,于是用单调栈处理出新加入的位置作为后缀的最大值的长度,随机数据情况下长度期望为 \(\log n\),暴力更新这段后缀,做一个其余部分保持不变但是累加贡献,可以发现这是一个历史和的形式,于是就可以拿下 \(52 pts\) 了。
暴力更新整个后缀过于麻烦,可以发现每个数最多入栈一次,我们如果在更新单调栈的时候每次对于一整个管辖区间进行更新,均摊单次是 \(O(1)\) 的。于是问题就变成了对于后缀最值 \(c_i,d_i\) 的区间修改,求 \(\sum c_id_i\) 的历史和。
我们设计信息为 \((sa,sb,sab,hab)\),懒标记为 \((da,db,sa,sb,hab)\),跑历史信息线段树即可,时间复杂度 \(O((n+q)\log n)\)。
ZROI 比赛
扫描线
U403634 糊纸
考虑扫描线扫 \(R\),维护 \(L\) 处的贡献 \(f_L\) 表示有多少 \(i\in [L,R]\) 满足 \([L,i]\) 两两互质。对于一组询问 \((l_i,r_i)\) 就直接在扫描到 \(r_i\) 的时候对于 \(f\) 进行 \([l_i,r_i]\) 的区间求和。
我们需要在 \(R-1\to R\) 的时候,对于满足 \([i,R]\) 两两互质的位置 \(i\) 进行 \(+1\)。不难发现对于满足要求的 \(i\) 是一段后缀,于是我们考虑求出最小的 \(i\) 满足 \([i,R]\) 内两两互质,记为 \(t_R\),然后对于 \([t_R,R]\) 进行区间加。
首先 \(t_R\) 满足双指针性质,也就说 \(t_R\ge t_{R-1}\)。其次对于 \(a_R\) 我们只要求出与其不互质的第一个点,然后 \(+1\) 之后和 \(t_{R-1}\) 取 \(\max\) 即可。
求出与 \(a_R\) 不互质的第一个点,我们可以维护每个质数出现过的最远位置,然后在 \(a_R\) 的质因数集内寻找即可,同时每次更新 \(a_R\) 质因数集合内的数最远位置为 \(R\)。值域范围内质因数个数不超过 \(7\) 个,因此是可以接受的。
CF983D Arkady and Rectangles
JOISC2019D ふたつのアンテナ (Two Antennas)
发现 \(i,j\) 对称,不妨假设我们要求的是 \(i<j\)。
可以直接对于询问进行扫描线,扫 \(j\),线段树维护 \(i\) 位置处的答案。
在扫描线扫到 \(i+l_i\) 时标记 \(i\) 可用,在扫到 \(i+r_i+1\) 时标记为不可用。只需要在扫描线扫到对应位置的时候插入删除即可。
然后对于每个 \(j\) 在 \([j-r_j,j-l_j]\) 中为 \(i\) 的可能集合。于是我们用 \(a_j\) 在线段树上区间更新即可,线段树上维护 \(\lvert a_j-a_i\rvert\) 的最大值。
实现方法是我们在线段树上维护五个标记 \(mx,mn,tmx,tmn,A\) 前两个表示区间 \(a_i\) 的最大最小值,中间两个表示区间 \(a_j\) 的最大最小值,最后一个表示区间的答案。一定要注意 \(i,j\) 要分开来维护,不能混用。每次就用 \(mx-tmn\) 和 \(tmx-mn\) 来更新答案即可。
上面还提到了 \(a_i\) 的插入与删除,其实做法就是把单点修改 \(mx\gets 0\),\(mn\gets -\infty\)。
时间复杂度 \(O((n+m)\log n)\)。
扫描线很平凡,但是维护方式很新颖的技巧。
时间复杂度 \(O((n+m)\log n)\)
ZROI2981.最后的战役
维护复杂信息
一些最大子段和之类的信息可以通过线段树上维护多种信息来合并得到答案。
ABC365F Takahashi on Grid
本题需要观察得到区间行走方式,并且分类。
在线段树上维护一二类区间的端点即可。
ZROI.2843 流苏花
先思考暴力,考虑 \(p\to l\) 的过程,我们反向思考从 \(l\) 开始推一个时间区间表示在当前点符合要求的开始时间。初始为 \((-\infty,\infty)\),每次 \(i\to i+1\) 的时候 \([L,R]\bigcap [l_i,r_i]\),由于 \(i+1\) 可以等待 \(t_{i+1}\) 的时间, 所以 \(L\gets L-t_{i+1}\)。就这么一直扩展,如果出现区间不合法那么就不合法了。
思考本质,对于 \(r\) 就是一直一个 chkmin 的过程,对于 \(l\) 也是一个不断减然后 chkmax 的过程,所以 \(l\) 就是 \(\max l_j-\sum\limits_{k=j+1}^{i-1}t_k\)。
考虑固定 \(r_i\),思考什么 \(l_j\) 会使得当前的 \(r\) 不合法,对于 \(j<i\),\(l_j-\sum\limits_{k=j+1}^{i} t_k>r_i\),对于 \(j>i\),\(l>r\)。对于第一个条件转化为 \(l_j-\sum\limits_{k=j+1}^nt_k>r_i-\sum\limits_{t=i+1}^n t_k\),记 \(a_j=l_j-\sum\limits_{k=j+1}^nt_k\),\(b_i=r_i-\sum\limits_{k=i+1}^nt_k\),维护 \(\max a_j,\min b_i, \max\limits_{j<i} a_j-b_i\) 即可。还有 \(\max l,\min r,\min\limits_{i<j} r_i-l_j\),支持进行区间修改。另一个方向的同理。
不过这个区间求和的东西更新起来也太麻烦了,明明是单点修改,但是最后却变成了区间修改。思考一下原因,因为我们要用到当前区间外的信息!那个 \(t\) 的求和式范围延展到了区间外。于是换一种维护方式,我们维护区间 \(\sum t\),尝试只利用区间内 \(\sum t\) 信息。在合并两个左右儿子的时候,我们可以在相交端点处判断是否合法,那么只需要记录 \(\max\limits_{i\in [l,r]} l_i-\sum\limits_{j=i+1}^{r} t_j\) 和 \(\min\limits_{i\in [l,r]} r_i+\sum\limits_{j=l}^{i}t_j\) 即可,每次早在区间交点处合并,正好把两部分 \(\sum t\) 合成了一个完整的。这样子只需要单点修改 \((l,r,t)\) 了。代码难度减小了很多。
时间复杂度 \(O(n+q\log n)\)。
兔队线段树
P4198 楼房重建
记斜率为 \(k_i\),对于每个区间维护区间 \(k_i\) 最大值,还有考虑整个区间 \([l,r]\) 之后,\([mid+1,r]\) 的答案。
CF671E Organizing a Race
一些额外功能
- 重构功能,对于支持快速合并的信息,如果需要重构,线段树是一个不错的选择,因为修改一个点只需要重构 \(\log\) 次。这个时候线段树本身是没有什么区间查询之类的作用的,它的唯一功能就是利用这个良好的结构进行少量重构。一个典型的例子就是 P2056 [ZJOI2007] 捉迷藏,下标是点的编号(其实是啥都无所谓),每个节点维护对应点集的直径,由于直径端点是支持合并的,所以这是对的。如果要求的是子树直径,把下标改为 dfs 序就可以了。
树状数组
\(c_i\) 维护的是 \((i-\operatorname{lowbit}(i),i]\) 的和。
- 后缀 BIT 就是把查询和修改操作跳 \(\operatorname{lowbit}\) 反过来,查询的时候就是 \((l)-(r+1)\)。
P3586 [POI2015] LOG
简单题,不过有一个地方不太好办。对于每次询问很显然的转化就是求是否 \(\sum\min(a_i,s)\ge s\times c\),把 \(a_i\) 拆成 \(a_i\) 个 \(1\) 相加,那么对于 \(s\),只要取前 \(s\) 个 \(1\) 即可。我们可以用动态开点线段树来维护,对于一个 \(a_i\) 就把线段树上 \([1,a_i]\) 集体加 \(1\),查询就是对于区间 \([1,s]\) 求和。可是这显然通过不了 \(10^6\) 的数据。
考虑使用小常数数据结构树状数组,可以树状数组可以维护的值域有限。我们只能维护相对大小关系,于是我们统计出 \(a_i\ge s\) 的个数,然后用 \(c\) 减去这些,再对于 \(a_s \le s\) 求和,这样子就成功将维护信息转化成了有相对大小的东西。
树状数组倍增
必须从头也就是 \(0\) 位置开始倍增,如果不是 \(0\) 零位置可以巧妙转化,不过不一定每一个模型都能转化,反正我在 APIO 2019 路灯上面成功转化过从任意位置开始倍增。
P6619 [省选联考 2020 A/B 卷] 冰火战士
类比课内数学题求 \(\max\limits_x\{\min\{f(x),g(x)\}\}\),一般都是两个函数交点部分吧。本题冰和火的分别能量和关于温度一个单增,一个单减。显然就是交点处可以最大化最小值,树状数组倍增维护一下即可。注意如果不是严格有一个整交点,要求出两边分别最逼近的整点。
KD-Tree
KD-Tree的精髓就在于剪枝,我们要设计出一个良好的估价函数。
KD-Tree非强制在线的插入,可以提前插入,然后打上激活标记。
下面给出一个例子,\(f_i=\min\{\sqrt{f_j+(A_i-A_j)^2}~|~0\le j<i,A_i \ge B_j\}\)
这是一个类似于 CDQ 分治斜率优化的问题,可以用 KDT 来查询。
加点 \((A_i,F_i^2)\),对应估价函数为 \(y_p+\max(x-x_1(p),x_0(p)-x,0)^2\)。
P2093 [国家集训队] JZPFAR
这里的估价函数就是记录每个节点各个方向延伸的最大长度,然后可以计算出每个维度的理论最远距离。用优先队列记录前 \(k\) 大,如果已经满了的话,进入一个节点条件就是理论最大值要大于队列中的最短距离。根据理论最远距离决定先走左孩子还是右孩子。
P4148 简单题
维护二维带修改求和。如果是可以离线的话像这种维护带修改二维信息可以用 CDQ 分治。但是本题在线。
KDT 如果动态加点可能会造成不平衡,于是我们引入平衡常数,如果最大的子节点的大小超过平衡常数倍的当前节点大小那么就暴力重构。重构就按照中序遍历找出所有子节点然后重构。
平衡树
来点科技,这玩意儿也就看一个乐,反正我是不会去用的,除非考试没时间了。
pb_ds
首先是头文件
#include <ext/rope>
using namespace __gnu_cxx;
定义:crope a,b[maxn];
\(\operatorname{push\underline~back}\) 末尾添加
\(\operatorname{insert(p,x)}\) \(p\) 位置后面加字符串 \(x\)
\(\operatorname{erase(p,x)}\) 删除 \(p\) 后面 \(x\) 个
\(\operatorname{replace(p,x)}\) 从位置 \(p\) 开始替换为 \(x\)
\(\operatorname{substr(p,x)}\) 提取 \(p\) 后 \(x\) 个
\(\operatorname{at(x)}\) 访问第 \(x\) 个
注意操作 2 4 都不包含 \(p\)
可并堆
可持久化左偏树
每个合并的时候,新建一个节点复制一份即可。
int merge(int x, int y) {
if (!x || !y) return x + y;
if (v[x] > v[y]) swap(x, y);
int p = ++cnt;
lc[p] = lc[x];
v[p] = v[x];
rc[p] = merge(rc[x], y);
if (dist[lc[p]] < dist[rc[p]]) swap(lc[p], rc[p]);
dist[p] = dist[rc[p]] + 1;
return p;
}
P2483 【模板】k 短路
先对于 \(n\) 建立最短路树,最短路径显然是最短路树上的路径,由于我们是要求 \(k\) 短路,所以需要用非树边进行拼凑。走出来的应该是一条树边与非树边交错的路。我们设 \(\Delta w\) 为加入一条非树边所用额外代价,\(\Delta w=dis_v+e_w-dis_u\)。
我们现在有两种操作,在边序列末尾加入边或者替换边。替换某条边则可以在末尾边起点以及其祖先那里选择非树边进行替换。加入则则是在末尾边的终点以及其祖先上选择非树边加入。用一个优先队列保存候选答案即可。
时间复杂度 \(O((n+m)\log n+k\log k)\)。
ODT
在数据随机,且有大量区间赋值操作的时候可以用。
原理就是用 set 来维护连续段。
set 的每一个元素都是一个以 \(l\) 为关键字比较的结构体,存着区间和对应的值。
首先是 split 操作,我们要把某个包含 \(pos\) 的区间分成 \([l,pos-1],[pos,r]\)。用 lower_bound 函数寻找即可,记得特判。
assign 区间推平操作。一定要注意先 split(r+1),再 split(l)。然后直接删除这一段,最后插入新的即可。
区间加,就是暴力遍历然后 \(+\)。
根号分治
应用技巧:一般多出现于有两个乘积小于等于定值时。一般其中一个根号计算较为简单,另一个根号计算感觉要难一点,还是要积累一下方法
AT_arc160_b [ARC160B] Triple Pair
题面中 \(xy \le n\) 不要被小于等于迷惑,此处依然可以使用根号分治。不过严谨来说不是根号分治,但是还是用这题提醒一下自己看到乘积大约为定值的时候考虑根号。以 $ \sqrt{n}$ 为分界点,\(x\) 和 \(y\) 必定有一个数小于 \(\sqrt{n}\) ,于是不妨设 $x \le y \le z $ ,此时 \(y \le \sqrt{n}\) 于是枚举 \(y\) 再乘法原理计数即可。
P5309 [Ynoi2011] 初始化
修改次数与修改周期乘积 \(\le n\) 。修改次数 $ \le T$ 时候直接暴力修改,修改次数 \(\ge T\) 时候说明每次修改的间隔很短。可以维护每一个修改周期下的修改位置。其实题目本质上就是在 \(mod\) \(x = y\) 的位置上增加值,于是对于每个模数 \(x\) 维护取模后值的前后缀和统计即可。
CF1039D You Are Given a Tree
P3396 哈希冲突
这个维护简单直接维护小于 \(T\) 的模数的池子,大于 \(T\) 的暴力累加即可。
笛卡尔树
应用:可以找数列中的每一个位置作为区间最小值的时候的最大区间。实际应用时可以用单调栈寻找。
01 Trie
下面是一些基本操作。
P6665 [清华集训2016] Alice 和 Bob 又在玩游戏 涉及了启发式合并,mex,整体异或一个数。
启发式合并:按层递归合并,合并到叶子节点的时候合并 \(sz\) 数组之类的,别忘记 pushdown 和 pushup。
mex: 看看左子树有没有填满,决定往左走还是往右走。
整体异或:pushdown 的过程中看看这层有没有被涉及到(tag>>d&1),如果涉及到了就交换左右儿子。
整体 \(+1\),首先必须从低位到高位建树,交换左右儿子,同时会对之前 \(ch_{u,1}\) 也就是现在的 \(ch_{u,0}\) 的子节点产生影响。于是递归继续修改即可。
P10218 [省选联考 2024] 魔法手杖
有一个可以用二分答案的思路,就是对于关键点建立虚树,然后压缩 trie,这样子树的大小就是 \(O(n)\) 了。时间复杂度 \(O(nk)\)。
支配对
点对贡献答案,但是可能的点对有 \(O(n^2)\) 种,不过有些是没有用的被其他点对偏序了,利用单调栈或者笛卡尔树结构可以找到 \(O(n)/O(n\log n)\) 对有用的点对然后对于这些点对进行扫描线。
- 需要注意有额外约束条件的时候,有的时候就无法使用支配对了。比如编号区间树上最小距离可以用,最大区间无法使用(构造一条 \(1-n\) 的链就可以卡成 \(O(n^2)\) 个),因为对于同一分治中心,不能选同一子树内的两个点,而最小距离可以忽视这个约束(多放点偏大的距离无影响,毕竟我们要求的是小的),最大距离不能忽视,就倒闭了。
序列问题,如果想要区间尽可能长就建立笛卡尔树,每个节点管辖的区间就是支配对了。如果想要区间尽可能短,那就单调栈。
树上问题考虑 dsu on tree 或点分治。如果是 LCA 相关选择前者,如果是距离相关选择后者。
P11392 [JOI Open 2019] 三级跳 / Triple Jump
支配对好题。
对于第一次跳跃的 \((i,j)\) 进行考虑,根据题目的跳跃约束条件 \(j-i\le k-j\),我们其实是希望其间距尽可能小。同时题目要求最大化 \(a_i+a_j+a_k\),我们肯定是希望 \(a_i+a_j\) 尽可能大。在这两个条件之下,我们可以发现对于 \((l,r)\),如果存在 \(l\le i < j\le r\),满足 \(a_i+a_j\ge a_l+a_r\),这个时候 \((l,r)\) 是没有用的,因为任何时候都可以将 \((l,r,k)\) 替换为 \((i,j,k)\) 这个调整是不劣的,因为 \((i,j)\) 在区间间距和权值两个维度都比 \((l,r)\) 优秀。
所以我们其实是要找出所有点对 \((l,r)\) 满足,\(\max\limits_{l<i<r} a_i< \min(a_l,a_r)\)。这个条件等价于建立小根笛卡尔树之后,某个点管辖的区间为 \([l+1,r-1]\)。由笛卡尔树的节点数可知,这样子的有效点对是 \(O(n)\) 对的。
确定前两个点的最优二元组之后,第三个点 \(k\) 需要满足 \(k\ge 2\times j-i\)。
对于区间询问转化为扫描线,用线段树下标为 \(k\) 的线段树维护区间 \(\max a_i+b_i\),同时支持对于 \(a_i\) 进行 chkmax。
时间复杂度 \(O(n\log n)\)。
P11364 [NOIP2024] 树上查询
可以用 dsu on tree 求出所有极长连续段,也可以直接利用结论区间 LCA 一定是区间内相邻两点 LCA 中的一个。
对于 \(k_i=1\) 特判一下。
对于 \(k_i>1\),令 \(r_i\gets r_i-1,k_i\gets k_i-1\)就是在 \([l_i,r_i]\) 之内找到一个区间 \([l,r]\) 满足区间长度 \(\ge k\),且 \(\min a_i\) 最大。
考虑求出所有支配对 \((l,r)\),然后对于区间分类。
-
\(l\le l_i\le r_i\le r\),直接二维偏序即可。
-
\(l\le l_i\le r\le r_i\),按照区间长度从大往小加入所有区间查找 \([l_i+k_i-1,r_i]\) 之内的最大值即可。
-
\(l_i\le l\le r_i\le r\) 同理类似第二种维护。
-
\(l_i\le l\le r\le r_i\),直接当成第二种即可。
时间复杂度 \(O((n+q)\log n)\)。
P9058 [Ynoi2004] rpmtdq
树上距离相关,考虑使用点分治求出支配对。
对于一个分治中心,我们求出其下所有点到它的距离。对于所有二元组,\((u,dis_u)\),按照 \(u\) 排序之后,对于 \(dis_u\) 建立单调栈,正反跑两遍找到每个点下标的前驱和后继即可找到支配对。注意每个点在每层分治中心之下产生 \(\le 2\) 个支配对,由于一个点会在 \(O(\log n)\) 层中出现,所以支配对的总数是 \(O(n\log n)\) 的。
使用扫描线 + BIT,时间复杂度 \(O(n\log^2n )\)。
猫树
P6109 [Ynoi2009] rprmq1
先考虑扫描线,扫 \(x\) 维度。矩阵加法可以用差分转化为两次区间加,然后对于矩阵 \(\max\),可以转化为执行时间 \([1,x_2]\) 内的操作,但是只统计时间 \([x_1,x_2]\) 内的区间历史最大值。
看到一段时间内的信息,可以用线段树分治来解决。但是这样子的话,由于每个询问会被分裂成 \(\log\) 个区间,所以最后 \(q\) 前面的系数会多一个 \(\log\),会造成对于 \(q\) 是 \(2\log\) 的。这样子会被卡常。于是我们采用猫树分治就可以去掉这个 \(\log\) 了。
由于是猫树分治,所以每一层内部使用扫描线,从左往右扫,对于加法操作,左加右减就行了。每次在询问右端点查询区间历史最大值,为了防止在不受到前面的影响,我们可以在进入左端点前给后面加上 \(\infty\),最后再减去即可。也可以打了一个标记,表示 \(his\gets mx\)。
时间复杂度 \(O(m\log^2n+q\log n)\)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号