字符串基础
KMP
\(Next_i\) 代表的是以 \(i\) 为终点的后缀和以 \(Next_i\) 为终点的前缀相等。
注意 \(Next_1\) 的值为 \(0\),若为 \(1\) 则成环。
经典应用: P4391 [BOI2009] Radio Transmission 无线传输
结论:若 \(i \bmod (i-next_i)=0\) 且$\dfrac{i}{i-next_i}>1 $,则 \(S\) 有长度为 \(i-next_i\) 的循环节。
P2375 [NOI2014] 动物园
求解 \(f_i\) 的时候跳到 \(\le \dfrac{i}{2}\) 处是错误的,会导致 \(f_i\) 求解的不正确。
于是我们考虑先求一遍 \(f_i\), 然后再来一遍类似的流程,只不过这次要求跳到 \(\le \dfrac{i}{2}\) 处。
P3193 [HNOI2008] GT考试
建立 KMP 自动机,设 \(g_{u,v}\) 表示有多少种添加字符的方式可以从自动机上的 \(u\) 节点转移到 \(v\) 节点。设 \(f_{i,u}\) 表示 \(X\) 串的前 \(i\) 位目前匹配状态是在 \(u\) 节点的方案数。\(g\) 的计算可以直接看看自动机上 \(u\) 有多少出边指向 \(v\)。
那么有 \(f_{i+1,v}\gets \sum\limits_{u} f_{i,u}\times g_{u,v}\),发现这是矩阵乘法的形式,于是直接上矩阵快速幂即可。时间复杂度 \(O(m^3\log n)\)。
QOJ5256. Insertions
给定三个串 \(S,T,P\),需要在 \(S\) 中插入 \(T\)(可以在开头或者末尾),求所有插入位置中与模式串 \(P\) 匹配次数最多的位置个数,最考前的位置,最靠后的位置。字符串长度均 \(\le 10^5\)。
一道很巧妙的字符串匹配题,并不需要用什么高级后缀结构。
题目给的三个小问启发我们其实应该是转化为求出在每个位置插入的匹配次数,而非单纯找一些最大的。
记 \(S,T,P\) 的长度分别为 \(n,m,p\)。
有一些很显然的匹配形式,假设我们在 \(S(i,i+1)\) 处插入字符串 \(T\),那么 \(S[1:i],S[i+1:n],T[1:m]\) 都是可以直接和 \(P\) 匹配的,这个可以预处理。
还有一些比较难处理,我们分成两类,一种是 \(S[l:i]+T[1,r]\) 或 \(T[l,m]+S[i+1,r]\),另一种是 \(S[l:i]+T+S[i+1,r]\)。
对于模式串 \(P\) 建立 fail 树。
对于第一种匹配两个类别是对称的,不妨讨论 \(S[l:i]+T[1,r]\),也就是一段前缀拼后缀。我们用 \(T\) 的前缀 \(T[1:j]\) 匹配 \(P\) 的后缀 \(P[p-j+1,p]\)(Z 函数可以统计),对于符合要求的匹配点 \(p-j+1\) 我们在 fail 树上标记一下这个点的上一个位置 \(p-j\)(代表如果 \(S\) 能匹配到 \(p-j\),就能和后面的连一起产生贡献) 。然后我们只需要在 \(S\) 上满足前缀要求即可,可以维护当前 \(S[1:i]\) 的后缀与 \(P\) 的前缀匹配的最长位置,所有满足 \(S[1:i]\) 的后缀与 \(P\) 的前缀匹配的位置都是上述的最长位置跳 fail 得来的,于是也就是当前点到根节点路径上标记点的个数。
对于第二类匹配类似地,我们找到所有的 \((l,r)\) 满足 \(T=P[l:r]\),同时必须满足 \(l\neq 1,r\neq n\),否则会会和前面的统计产生重复贡献,标记二元组 \((l-1,r+1)\)。建立 \(P\) 的正反串 fail 树,然后就变成了一个两颗树上数两个点到根节点公共点个数的 ds 题,注意此处的公共点表示可以构成被标记的二元组 \((l,r)\)。做法类似于 IOI2018 werewolf 是对于标记点对 \((p,q)\) 改为 \((dfn_p,dfn_q)\),注意两个 \(dfn\) 不同,分别表示在两颗树上 dfs 序。我们用扫描线来扫描第一颗树的 dfs 序,线段树维护第二颗树的 dfs 序,每次进行区间修改,单点查询即可。
\(n,m,p\) 视为同阶,时间复杂度 \(O(n\log n)\)。
KMP自动机
和 AC 自动机一模一样,唯一区别就是 AC 自动机是多个串之间各个状态的转移,而 kmp 自动机是单串。由于多串需要字典树辅助一下,单串不需要字典树,因为 \(s_i\) 之后只有 \(s_{i+1}\) 这个选择。于是就同理建立就行了,AC 自动机上的 fail 数组就是 kmp 中的 \(f\) 数组。
CF1721E Prefix Function Queries
最直观的解法就是我们先对于串 \(s\) 求一遍 kmp。然后对于加入的后缀 \(t\) 接到 \(s\) 后面,对于串 \(s+t\) 从 \(\lvert s\rvert+1\) 位置开始跑 kmp。
但是这个复杂度是错的,因为思考原版 kmp 是如果保证复杂度的,由于每次指针最多往后移动一位,所以我们的指针 \(j\) 向右的移动量最大为 \(n\)。因此向左的最大移动量也为 \(n\),这个是依赖均摊做到 \(O(n)\) 的。
但是如果这次我们还均摊的话,会把 \(\lvert s\rvert\) 也给摊上,做 \(q\) 次显然是不对的。思考如果加速 \(s\) 部分的转移,我们建立 kmp 自动机,对于每个位置往后加一个字符跳到哪里直接做一个链接,这样子在 \(i\le \lvert S\rvert\) 的部分就可以 \(O(1)\) 直接跳了。于是复杂度就正确了。
CF1575H Holiday Wall Ornaments
多模板串约束可以用 ACAM,对于单模式串我们同样可以建立 KMP 自动机来模拟赛匹配过程的变化,在自动机上 dp 即可,时间复杂度 \(O(n^3)\)。
ZJU训练题 整洁度
对于两个串,其整洁度为最长公共 border 的长度。求一个串的所有前缀任意排列之后,相邻整洁度之和。同时有 \(m\) 次修改,每次在末尾添加或者删除字符。\(n,m\le 5\times 10^5。\)
好题,可惜是内部题,无提交通道。
第一步是很显然的转化 P5829 【模板】失配树,就是离线求出 fail 树上 LCA 深度之和。
如何重排?有一个结论就是按照 dfs 序重排就是最优的。
离线建树之后,加减关键点,直接按照 P3320 [SDOI2015] 寻宝游戏 里面的方法用 std::set 维护 dfs 序即可,可以支持动态维护。
考虑如何建树,每次加字符就是要求出该点的 \(f\)。动态加减字符可能会让建树复杂度爆掉,我们直接建立 KMP 自动机就行了。
如果只有动态加字符很好做,就按照 CF1721E 里面的做法就行了。本质是如果一个字符会被后面多次添加影响到就需要建立自动机,但是你有了删除操作之后,你可以不断删除再添加,所以我们要对于每个新加入的点都动态建立自动机。
border 理论
周期:\(s_i=s_{i+T}\),就是可以把 \(s[1:T]\) 不断往后复制(最后一次复制可以只复制一部分)。
如果 \(s\) 有 \(\ge \frac{n}{2}\) 的 border \(i\),那么就有 \(n-i\) 的周期,如果 \(n-i\mid n\),那么就有循环节了。
字符串 \(S\) 的 border 集合等于其最长 border 的 border 集合并上 \(S\)。
字符串 \(s\) 所有不小于 \(\dfrac{\lvert s \rvert}{2}\)的 \(border\) 构成等差数列。
从周期角度理解,每次都是减少一个周期长度
可以把字符串的所有 border 长度分成 $\log \lvert s \rvert $ 段,每一段的 border 构成等差数列。
设 \(S\) 的最长 border 为 \(T\),那么 \(S\) 有 \(\lvert S\rvert-\vert T\vert\) 的周期。
于是对于 \(\vert R\rvert \equiv \vert S\vert \pmod{\lvert S\rvert-\vert T\vert}\) 的 \(\vert R\vert\),都是 \(S\) 的 border。以这个为开头来划分等差数列,由于每次取模都是减少一半的所以最多有 \(\log\) 段。
周期引理
对于串 \(S\) 的两个周期,如果满足 \(a+b-\gcd(a,b)\le\lvert S\rvert\),那么 \(\gcd(a,b)\) 也是一个周期。
ARC077F
很好的字符串周期题。
下文中讲题目所给的偶串 \(S\),表示为 \(SS\),也就是将其拆开表示。
考虑一次 \(f\) 变换中,\(SS\to S'S'\),当 \(S'=SS\) 的时候显然是最直观的变法,保证了是偶串但是不保证最短。所以我们考虑不用那么多,将第二个 \(S\) 拆分为 \(U+T\),然后令 \(S'=SU\),此时就是 \(SUT\to SUSU\),可以发现此时必须满足 \(T=\operatorname{prefix}(S)\),又因为此时 \(U\) 也是 \(\operatorname{prefix(S)}\)。
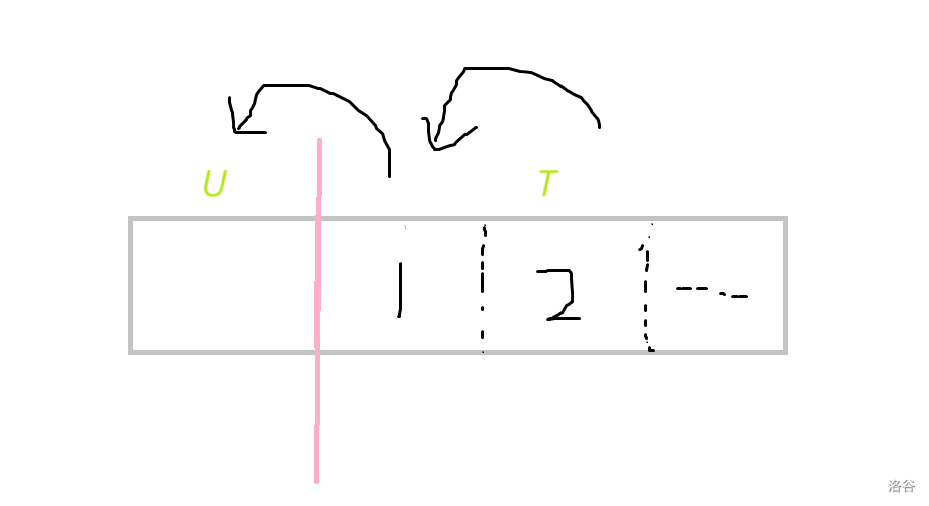
画个图可以发现 \(U=T_1,T_1=T_2...\)
由此可以得到 \(U\) 是 \(S\) 的周期,又因为要求长度尽可能短,所以 \(U\) 是 \(S\) 的最短周期。
上述讨论明确了 \(f(SS)\) 变换之后的结果。但是我们不能每次 \(f\) 变换都跑一遍 kmp 来找到周期,这样子太慢了。
考虑进一步寻找规律。
对于 \(\lvert S\rvert \bmod \lvert U\rvert=0\) 的情况,变换就是 \(SUSU\to SUUSUU\to SUUUSUUU\to ...\),由于是无限复制,所以只用看前半部分即可,也就是 \(SUUU...\),这个好算,直接找到 \((l,r)\) 对应的部分,分整散块处理一下即可。
对于 \(\lvert S\rvert \bmod \lvert U\rvert\neq 0\) 的情况就复杂点。这里给出结论此时 \(S\) 是串 \(SU\) 的最短周期。证明如下
采用反证法,假设存在比 \(S\) 更小的周期 \(P\)。
那么此时 \(P\) 也是 \(S\) 的周期,又因为 \(U\) 是 \(S\) 的最短周期,所以 \(\lvert P\rvert>\lvert U\rvert\)。
因此对于 \(i\in[\lvert S\rvert+1,\lvert S'\rvert]\),有 \(S'_i=S'_{i-\lvert S\rvert}=S'_{\lvert P\rvert}\)。
又因为上面得到了 \(\lvert P\rvert>\lvert U\rvert\),所以 \(i-\lvert S\rvert,i-\lvert P\rvert\le \lvert S\rvert\)。
根据 \(S\) 有周期 \(U\) 可知,\(i-\lvert S\rvert\equiv i-\lvert P\rvert \pmod{\lvert U\rvert}\)
故 \(\lvert S\rvert\equiv \lvert P\rvert \pmod{\lvert U\rvert}\)。
又因为 \(\lvert S\rvert> \lvert P\rvert\),所以 \(\lvert S\rvert\ge \lvert P\rvert+\lvert U\rvert\)。
根据弱周期引理有 \(S\) 有周期 \(\gcd(\lvert P\rvert,\lvert U\rvert)\)。
又因为 \(\lvert S\rvert\equiv \lvert P\rvert \pmod{\lvert U\rvert}\),且 \(\lvert S\rvert \bmod \lvert U\rvert\neq 0\)。所以 \(\lvert P\rvert\) 不是 \(\lvert U\rvert\) 的倍数,故 \(\gcd(\lvert P\rvert,\lvert U\rvert)<\lvert U\rvert\),这与 \(U\) 为最短周期不符合。
故矛盾,所以 \(SU\) 的最短周期为 \(S\)。
于是变换就是 \(SS\to SUSU\to SUSSUS\to SUSSUSUSSU...\)
还是只用考虑前半部分,这是一个斐波那契数列,增长速度近似于指数级,于是我们暴力递推斐波那契数列算贡献即可在 \(\operatorname{ploylog}\) 的复杂度内解决问题。
P1393 Mivik 的标题
如果按照 P3193 的 trick 来做的话是 \(O(\lvert S\rvert^3\log n)\) 的。
观察到本题和那题的区别其实是 \(\lvert S\rvert\) 大,但是 \(n\) 小。所以考虑对于 \(n\) 进行 dp 之类的。
一个串内可能多次出现 \(S\),为了不统计重复,我们在其第一次出现的时候统计他。设 \(f_i\) 表示 \(S\) 第一次出现在以 \(i\) 结尾的位置。那么后面就随便填了。
我一开始想太简单了,我觉得既然是第一次出现,我们就拿出现的方案数减去之前的 \([1,i-1]\) 之内的 \(f\) 乘以一个系数之类的不就行了吗?但其实有点小问题,因为我们已经钦定了 \([i-\lvert S\rvert+1,i]\) 之内的串为 \(S\),所以 \([1,i-\lvert S\rvert]\) 之内的 \(f\) 是不受影响的,可以乘以一个系数减去,但是 \([i-\lvert S\rvert+1,i]\) 之内的需要有限制不是随便填的。
具体来说,必须满足在 border 处的 \(f\) 才有可能造成重复贡献。因为在这些地方满足前缀和后缀是相等的,恰好可以放入。
如果暴力找 border 处的 \(f\),时间复杂度是 \(O(n\lvert S\rvert)\) 的。
运用 border 理论,\(S\) 的所有 border 都可以被划分为 \(\log\) 个等差数列,记录等差数列前缀和就可以 \(O(\log \lvert S\rvert)\) 转移。
时间复杂度 \(O(n\log \lvert S\rvert)\)。
失配树
\(KMP \to fail\) 树。Fail 树上可以得到一个 \(S[1:i]\) 的某个后缀作为 \(S\) 前缀出现的信息,详见上面的 QOJ5256。
P5829 【模板】失配树
两个前缀的 border 就是他们在 fail 树上的 lca。
Manacher
首先为了避免分类讨论,我们应该统一奇偶,在所有串每个空隙(包括首尾)之间插入一个无关字符,这样子回文中心就一定是某个字符了,而非空隙。
可以得到原串中最长回文子串的长度等于新串最长回文子串的半径减一,即 \(d=R-1\)。不是最长的未必满足这个性质。
我们维护当前右端点最远的对称中心 \(c\),设其半径为 \(r_c\),右端点为 \(R=c+r_c-1\)。设我们当前在考虑位置 \(i<R\),那么 \(i\) 关于 \(c\) 的对称点就是 \(2c-i\),
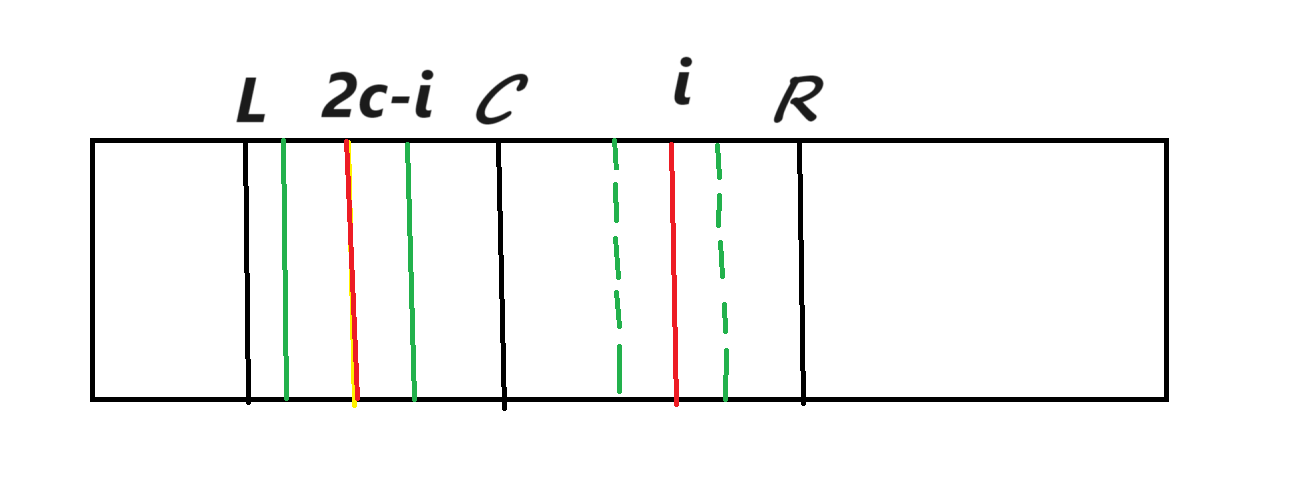
观察这张图,我们发现在 \(2c-i\) 地方的小区域对称正好也可以通过 \(c\) 点对称到 \(i\) 点来,但是注意如果 \(2c-i\) 的对称左端点越过了 \(L\) 就意味着多出来的那一部分无法通过 \(c\) 点传递我们也无法确认。于是 \(r_i \gets \min(r_{2c-i},R-i+1)\)。如果 \(r_i\) 取的是前者,那就意味着后面已经无法再继续匹配了,直接终止,如果取的是后者,我们暴力继续往外扩展即可。
可以发现最远右端点的移动的是 \(O(n)\) 的。所以时间复杂度线性。
这也可以证明一个字符串的本质不同回文子串个数不超过 \(n\) 个。
写代码时千万别忘记在开头加上分隔字符。
P4555 [国家集训队] 最长双回文串
我们只要求出 \(x_i\) 与 \(y_i\) 表示原串中以 \(i\) 开头和结尾的最长回文子串的长度即可,然后 \(\max x_i+y_{i+1}\) 拼接即可。如果求 \(x_i\) 呢?首先原串的每个位置 \(i\),在加入额外字符之后会变成 \(2\times i\),于是我们只要在新串的偶数位置更新即可,自己模拟几种情况我们可以发现 \(x_{i/2}=\max\limits_{c+r_c-1\ge i}\{i-c+1\}\)。除以 \(2\) 是因为要映射回原串,为了满足 \(c+r_c-1\ge i\) 的要求,我们在每次 \(i+r_i-1 > R\) (不能取等) 的时候暴力用 \(i\) 作为中心更新 \((R,i+r_i-1]\) 即可。
UVA11475 Extend to Palindrome
有点构造题的感觉。找到最小的 \(l\),满足 \([l,n]\) 为回文,然后直接将 \(s[1,l-1]\) 翻转后放到末尾即可。
P5446 [THUPC2018] 绿绿和串串
被硬控了。改改调调了半天。
考虑翻转一次是好做的,直接判断 \(i+r_i-1=n\) 即可。
翻转多次的话首先需要 \(i=r_i\),其次要翻转之后的那个末尾点也作为答案点(这样子才能继续往后翻)。
于是求出 \(r_i\) 之后,我们对着字符串倒着扫一遍处理答案即可。
exKMP
\(z_i\) 表示字符串 \(s\) 与 \(suf_i\) 的最长匹配长度,其中 \(z_1=n\)。
对于 \(z\) 的求法与思想 Manacher 类似,称 \([i,i+z_i-1]\) 为匹配段,我们只要维护最靠右的匹配段即可,记为 \([l,r]\)。假如当前考虑到了 \(i\),对于 \(i>r\),我们暴力匹配,对于 \(i\le r\),我们可以通过之前求出的结论得到 \(s[i,r]=s[i-l+1,r-l+1]\),这不正好和 \(z_{i-l+1}\) 有关吗,于是 \(z_i \gets \min(r-i+1,z_{i-l+1})\)。
和 Manacher 同理就是右端点的移动是线性的,所以复杂度为 \(O(n)\)。
CF432D Prefixes and Suffixes
首先用 KMP 匹配可以求出所有前缀等于后缀的地方。
然后这其实是一个关于前缀计数的东西,我们要统计出某些前缀在串中出现了几次,我们发现较短的前缀被包含在较大的前缀中,如果位置 \(i\) 的 \(Z\) 函数为 \(z_i\),那么 \([1,z_i]\) 的前缀都出现过,直接差分即可。
PKUSC2023 Border
面对这种类似单点修改全局查询的东西,且各个操作独立的题,一定要注意信息变化量很小,且只允许一个信息与原始的偏差。一个偏差意味着如果可以在替换情况下构成 border,那么我们找到第一个不符合条件的位置,然后它的前后必然都是符合条件的,并且该位置可以被符合条件的替换。
形式化地来说,可能产生贡献的位置必须满足之前 \(s[i,n]\) 和 \(s[1,n-i+1]\) 之间最多有一个位置不同。可以想到用 Z 函数。对于我们对于 \(i\) 找到 \(i+z_i\) 这个位置代表是第一个不同的位置。此时有两种可能,一种是 \(s_{i+z_i}\to t_{i+z_i}\) 之后符合条件,另一种是 \(s_{z_i+1}\to t_{z_i+1}\) 之后符合条件。我们对于两种分别判断即可。
于是本题的答案统计就以下几个部分:
- \(s_i=t_i\),那 \(ans_i\) 就是 \(s\) 的最长 border。
- \(s_i\neq t_i\),最基本的就是找到一个最长 border,其长度 \(l\) 满足 \(l<i<n-l+1\),这一部分可以对于序列前后两半分别扫描一遍统计。还有一种就是上文提到的替换后的贡献。
P5334 [JSOI2019] 节日庆典
ARC058F 文字列大好きいろはちゃん
Trie
01 Trie 就不在字符串这里记录了。
P7537 [COCI2016-2017#4] Rima
先考虑暴力,就是两两算一下能不能押韵,然后建边,以每个点为起点跑一遍最长链。
我们可以在字典树上解决这个问题,我们建反串,仔细思考一下这个问题,其实就是在从一个节点开始在字典树上行走,每次可以到父亲或者同父的兄弟,问最多能到达多少节点,树形 dp 一下即可。
AC自动机
\(\mathrm{Trie}\) 树 \(\to\) \(\mathrm{Trie}\) 图。
构建过程:先建立 Trie 树,然后把与根相连的第一个字符入队,同时 \(f\) 设为 \(0\),防止自环。然后开始扩展,如果当前 \(r\) 点没有字符 \(c\),那么 \(ch_{r,c}\gets ch_{f_r,c}\)。否则入队,然后 \(f_u\gets ch_{f_r,c}\),同时更新 \(last\) 数组,如果 \(f\) 位置有尾节点,那就是 \(f\) 了,否则就是 \(last_f\)。
bfs 性质保证了长度小的串先被遍历到,所以 \(f\) 与 \(last\) 数组一定可以保证连到。
CF710F String Set Queries
三种做法。
二进制分组
二进制分组,发现每一个字符串最多被重构 \(\log n\) 次,于是时间复杂度为 \(O(n\log n)\)。我们发现到答案的可减性,于是可以建立两个 AC 自动机分别负责添加和删除然后最后的答案就是添加组减去删除组。这里注意写法,直接创立两个个 AC 自动机的结构体,数组都在结构体里面开,每次调用不同结构体即可这样代码难度就减了很多。
实现细节,用每次当 \(sz_{top}=sz_{top-1}\) 的时候进行合并,合并的过程就是对应节点 \(val\) 相加。为了方便维护,我们在 getfail 的时候不能随便连 ch 了,必须新建立一个 sh 来连。
一种很典的做法
神奇的思路,我们设 \(\sum \lvert S_i \rvert=m\),于是\(\lvert S_i \rvert\) 的不同个数为 \(O(\sqrt n)\) 级别,每次枚举 \(T\) 中长度为 \(\lvert S_i \rvert\) 的字串,然后哈希判断即可。
根号分治
根号分治,较短串用字典树维护,较长串用 KMP 维护。
P2444 [POI2000] 病毒
直接在 AC 自动机上不碰到尾节点搜索,如果有环就可以无限绕着环走,这样是安全的。
注意有向图判环不能 \(0~1\) 标记,应该是 \(0~1~2\) 标记。
P2414 [NOI2011] 阿狸的打字机
经典 Trick:\(x\) 在 \(y\) 中出现可以转化为 \(y\) 中某个位置跳 fail 可以跳到 \(x\) 的终止节点。其中某个节点代表匹配上的最后一个位置。
我们发现其实就是对每个串建立一个 KMP,多个串的 KMP 自然就想到了 AC 自动机。
每次查询对于 \(y\) 链上的每个子串暴力跳 fail 的话太慢了,可以离线存下所有询问对于每个 \(y\) 链一起跳。
其实反过来考虑,这本质就是一个 \(x\) 的 fail 树的子树对于 \(y\) 求和问题。我们发现 \(y\) 是 AC 自动机上的一条链。于是可以顺着 AC 自动机的边走,进入累加,离开减去。这样所有时刻被累加的都是一条链上的贡献。
注意上述沿着 AC 自动机的边,指的是未创立 fail 之前的边,否则会成环。
CF163E e-Government
很套路的典题。
多模式串考虑建立 ACAM。
考虑如果刻画一个串 \(x\)(集合中的串)在另一个串 \(y\)(询问串)中是否出现/出现次数。我们用 \(y\) 在自动机上跑匹配,\(x\) 在 \(y\) 中出现是在 \(y\) 中某次到达(匹配过程中经过的节点,该状态为 \(y\) 的一个前缀)的状态跳 fail 可以跳到 \(x\)。也就是 \(y\) 中的某个状态在 \(x\) 的子树中,如果从最后的匹配来看,该位置也是匹配的末尾点。
于是问题就很简单了,我们反向考虑贡献,对于每个 \(x\) 都对其子树 \(+1\),这样子我们把 \(y\) 一路经过节点的权值累加就是最后的答案了。
考虑从集合中的删减,本质也就是子树的加减动态修改,BIT 维护即可。
时间复杂度 \(O(n\log n)\)。
CF547E Mike and Friends
首先建立 AC 自动机。
我们将 \([l,r]\) 拆成 \([1,r]-[1,l-1]\),然后进行扫描线,每次动态加入一个字符串就是相当于对于该串的所有状态节点加一,询问就是子树求和。
CF587F Duff is Mad
DP
其实 AC 自动机上 dp 一般就是出现某种些字符串可以得分或者某些字符串禁止出现。
前者是 P5319 [BJOI2019] 奥术神杖,后者是 ZROI2979.数数。
Shift-And 算法 / Bitset 优化字符串匹配
基本思路:用 std::bitset 移位求出模式串的每个终止位置。
我们建立 \(|\Sigma|\) 个 std::bitset \(c_*\),表示字符 \(*\) 在文本串 \(S\) 中出现位置,在对应出现位置权值为 \(1\)。
对于每次询问的模式串 \(T\),我们先开一个 std::bitset \(B\) 表示 \(T\) 与 \(S\) 匹配之后可能的结束位置。
我们枚举 \(T\) 的每一位 \(T_i\) 都将 \(c_{T_i}\) 左移 \(|T|-i\) 位和 \(B\) 按位与(注意二进制里面的左移是变大)。
最后得到的 \(B\) 中为 \(1\) 的位置集合,就是 \(T\) 与 \(S\) 匹配后 \(T\) 最后一个字符可能在的位置。
CF914F Substrings in a String
如果不带修改,就是对于询问串建立 ACAM,然后跑一遍文本串。但是带修改就很邪恶了。
很经典的题目,目前有三种解法。
- bitset 匹配
修改操作可以 \(O(1)\) 对于涉及到的两种字符的 bitset 作单点修改。
查询就是进行上述匹配后,求 \(B\) 区间内 \(1\) 的个数。区间是 \([l+|T|-1,r]\),特判一下 \(|T|>r-l+1\) 的情况后,答案就是 (B>>l+m-1).count()-(B>>(r+1)).count()。
时间复杂度 \(O(\dfrac{|S|(\Sigma |T|)}{\omega}+q)\)。
- 根号分治
这其实是一个 kmp 的过程。但是如果对于所有串都跑一遍 kmp 的话又太慢了。我们进行根号分治,大于阀值 \(L\) 的查询我们直接进行 kmp 匹配,这种串不会超过 \(\frac{\sum |T|}{L}\) 个。有一个优点就是反正我们是每次重构 kmp 数组,所以修改对它不会产生影响。
对于长度小于阀值 \(L\) 的查询,我们维护从每个下标开始的不超过 \(L\) 的每个哈希值。每次查询就是找 \([l,r-|T|+1]\) 的所有位置的长度为 \(|T|\) 的哈希值中和 \(T\) 相等的。这等价于在一个 \(L\times n\) 的平面内,求某一行的一个区间中等于 \(\rm Hash(T)\) 的元素个数。如果不带修改的话容易离线下来对于每一行作扫描线,带修改的话我们就需要对于平面的列进行分块,块长为 \(B\)。现在有 \(O(\dfrac{|S|}{B})\) 个块,每次块内维护 \(L\) 个 std::unordered_map 来保存哈希值对应的元素个数。修改的话就是暴力 \(O(L^2)\) 修改所有被影响到的位置即可。
时间复杂度 \(O(\dfrac{|S||T|}{L}+qL^2+q(\dfrac{|S|}{B}+B))\)。取 \(B=\sqrt {|S|},L=\sqrt[3]{\dfrac{|S||T|}{q}}\) 即可。\(L\) 可以往小调,因为 \(O(qL^2)\) 那一部分访问哈希表的常数很大。
- SAM \(+\) 分块。
对于 \(|T|>L\) 的询问,我们暴力建出区间的 SAM,然后查询出现次数。
对于 \(|T|\le L\) 的询问,考虑按照 \(L\) 对于序列分块,\(T\) 只有可能在块内和相邻两个块间出现。我们维护块内的 SAM,如果有修改就暴力重构即可。每次查询对于散块就是暴力建立 SAM,对于整块直接查询,对于块间的位置为了防止查到块内的出现位置,我们取分界点左右长度为 \(|T|-1\) 的段来建立 SAM(这部分的复杂度是 \(L\sum |T|\))。
取 \(L=\sqrt{|S|}\) 即可。总的时间复杂度 \(O(|S|\sqrt {|S|})\)。
CF963D Frequency of String
以下默认 \(n,q,|S|\) 同阶。
发现只需要找到询问串的 endpos 集合,找到最小的区间覆盖 \(k\) 个集合内的点就行了。显然可以直接双指针遍历这个集合,但是时间复杂度是 \(\sum size(endpos)\) 的。
本题最重要的一点是保证询问串两两不同,这里需要用到一个结论:
\(n\) 个不同的(长度之和为 \(L\) 的)串在同阶长度的中的文本串中的 endpos 集合大小为 \(O(n \sqrt{L})\)。
考虑证明:长度相同的不同子串的 endpos 集合大小 \(\le n\),由于询问串总长为 \(L\),那么一共有 \(O(\sqrt L)\) 种不同的长度,故总的 endpos 集合大小不超过 \(O(n\sqrt L)\)。
所以我们只需要求解
- bitset 匹配
可以发现上述算法求的正是 endpos 集合,那么如何取出 bitset 里面为 \(1\) 的位置呢?使用 _Find_first() 和 _Find_next(x) 函数即可。
时间复杂度 \(O(\dfrac{n^2}{w}+n\sqrt n)\)。
- SAM
在 parent 树上,使用线段树合并即可。但是由于要保存历史信息写起来很麻烦。
- 根号分治
考虑一个暴力做法,每次用哈希匹配字符串,暴力扫描,找到所有 \(m_i\) 出现位置,用双指针求解答案,我们采用根号分治,对于长度大于 \(B\) 的询问串,执行上述算法。
对于长度小于 \(B\) 的串,先找到文本串中所有长度 \(\le B\) 的 \(nB\) 个串,将他们与询问串匹配(这一步等价于暴力找到了所有串的 endpos 集合)。对于每个询问,在其对应的 endpos 集合内暴力扫一遍做匹配即可。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号