离散对数问题
离散对数问题
通常是解决 \(\bmod p\) 意义下 的 \(\log _ a b\) 这样的问题,等价于解 离散对数方程
这样的 \(x\) 可能有 零个,一个 甚至 多个,我们目的即是 找到这样的一个 \(x\)
当 \(a \perp p\) 时,我们一般使用 \(BSGS\) 解决,否则可以使用 \(exBSGS\) 解决
全文 绝大多数 内容是对 [0] 中讲述的 粗略抄写 和 胡乱加工
1. 大步小步算法
\(BSGS\),全称 \(Baby ~ Step ~ Giant ~ Step\),适用于在 \(a \perp p\) 的情形下解决 离散对数方程
核心是 根号平衡 的思想,根据 欧拉定理*,原方程若 有解 则必有一解在 \([1, p - 1]\) 中
故若设块长为 \(B\),则 \(x\) 可以表示成 \(pB - q\) 的形式,其中 \(q \in [1, B)\),原方程即
考虑枚举 \(i, j\) 以求解,只需用 哈希表 记录 出现过的余数,然后类似 \(meet ~ in ~ middle\)
就可以在 \(O (\max (i, j))\) 的时间内求解答案,显然,一般情况下,\(B = \sqrt p\) 时 最优
此时 \(i _ {\max} = \dfrac p B = \sqrt p\),\(j _ {\max} = B - 1 = \sqrt p - 1\),即时间复杂度 \(O (\sqrt p)\)
inline int Qpow (int a, int b, const int p);
inline int BSGS (const int a, const int b, const int p) {
static std::unordered_map <int, int> Vis;
int B = sqrt (p) + 1, P = Qpow (a, B, p), K = 1, Ans = (1ll << 31) - 1;
for (int i = 1; i <= B; ++ i)
K = 1ll * K * P % p, Vis[K] = i;
K = b;
for (int i = 0; i < B; ++ i) {
if (Vis.count (K)) Ans = min (Ans, Vis[K] * B - i);
K = 1ll * K * a % p;
}
return (Ans == ((1ll << 31) - 1)) ? -1 : Ans;
}
Luogu P3846 [TJOI2007] 可爱的质数 /【模板】BSGS
就是纯纯板子,注意要求输出 最小解
#include <bits/stdc++.h>
using namespace std;
inline int Qpow (int a, int b, const int p) {
int Ret = 1;
while (b) {
if (b & 1) Ret = 1ll * Ret * a % p;
a = 1ll * a * a % p, b >>= 1;
}
return Ret;
}
inline int BSGS (const int a, const int b, const int p) {
static std::unordered_map <int, int> Vis; Vis.clear ();
int B = sqrt (p) + 1, P = Qpow (a, B, p), K = 1, Ans = p;
for (int i = 1; i <= B; ++ i)
K = 1ll * K * P % p, (!Vis[K]) ? Vis[K] = i : 0;
K = b;
for (int i = 0; i <= B; ++ i) {
if (Vis.count (K)) Ans = min (Ans, Vis[K] * B - i);
K = 1ll * K * a % p;
}
if (a % p == 0) return b % p == 0 ? 1 : -1;
return (Ans == p) ? -1 : Ans;
}
int b, p, n;
signed main () {
cin >> p >> b >> n;
int Result = BSGS (b, n, p);
if (Result == -1) cout << "no solution" << '\n';
else cout << Result << '\n';
return 0;
}
虽然 本题保证了 \(a < p\),但是 不能忽视有些时候 \(p \mid a\) 的情况,比如 第一道经验
这个板子题 经验很多,可以帮助完善 各种细节,代码在每个 EXP 对应链接里
EXP - 1 - Luogu P4028 New Product(注意 \(p \mid a\),以及 同余数取最小值)
EXP - 2 - Luogu P2485 [SDOI2011] 计算器(注意 \(p \mid a\) 且 \(p \mid b\) 时,小心乘法爆掉 int)
EXP - 3 - Luogu P4454 [CQOI2018] 破解D-H协议(知道 \(g ^ a, g ^ b, g, P\),求 \(g ^ {ab}\),降蓝了!)
Luogu P3306 [SDOI2013] 随机数生成器
需要 推一些狮子,我们设 \(s_i \equiv \dfrac {x_i} {a ^ i} \pmod p\),于是
显然有 \(s_0 = x_0\),则 \(s_i = x_0 + \sum \limits _ {j = 1} ^ {i} \dfrac b {a_j}\),之后我们可以表示出 \(x_i\)
之后我们把 \(\dfrac b {a - 1}\) 挪到 左边 去,原式就成了 \(ca ^ i \equiv b \pmod p\) 的形式,\(BSGS\) 乱搞一下就行
注意到 \(a = 0, a = 1, b = 0\) 的情况,十分恶心,具体可以看我的 特判
int T;
int A, B, X, P, Q;
inline void Solve () {
cin >> P >> A >> B >> X >> Q;
int Rev = Qpow (A - 1, P - 2, P), Fac = 1ll * B * Rev % P, Result, Waste;
if (X == Q) {
Result = 0;
} else if (A == 0) {
Result = -2;
if (Q == B) Result = 1;
if (Q == X) Result = 0;
} else if (A == 1) {
EXGCD (B, P, Result, Waste);
Result = 1ll * Result * (Q + P - X) % P;
Result = (Result % P + P) % P;
if (B == 0) Result = (Q == X) ? 0 : -2;
} else
Result = BSGS (A, (Q + Fac) % P, P, (X + Fac) % P);
cout << Result + 1 << '\n';
}
板子太长,依旧没有什么 放出来的价值,完整代码
EXP - 1 - Luogu P4884 多少个 1?(\(a = 10, b = 1, x_0 = 1\),注意 long long 的开)
CF1106F Lunar New Year and a Recursive Sequence
\[\begin {aligned} f_i = \begin {cases} 1 ~ (i \in [1, k)) \\ q ~ (i = k) \\ \prod \limits _ {j = 1} ^ k { f_{i - j} ^ {b_j} } ~ (i \in (k, n]) \end {cases} \end {aligned} \]给出 \(f_n = m\),试求 \(q\) 的 可能值
不会线性代数基础的痛
一般我们认为 \(\prod\) 较难处理,考虑将其转化成 \(\sum\)
容易想到 取对数 这个经典操作,但这是在 模意义下,所以考虑 离散对数
设 \(f_i\) 的 离散对数 为 \(l_i\),于是 \(l_i = \sum \limits _ {j = 1} ^ {k} b_j l_{i - j} \pmod {\varphi (p)}\)
我们可以用 矩阵乘法 来表示这个东西
容易发现,我们的转移矩阵是一个 确定的矩阵 \(\textbf A\),我们需要这样转移 \(n - k\) 次
故我们可以对 转移矩阵 做 矩阵快速幂,然后通过 原始矩阵 乘上 转移矩阵 直接得到结果,即
我们注意到,\(l_1, l_2, ..., l_{k - 1}\) 对应 \(f_1, f_2, ..., f_{k - 1}\) 的 离散对数,即 \(1\) 的 离散对数,为 \(0\)
而我们只关心 \(l_n\) 的值,于是根据上述等式,我们可以得到下面的 同余式
而 \(l_n\) 可以 \(BSGS\) 快速求出,\(\textbf A ^ {n - k} _ {k, k}\) 矩阵快速幂 易得,于是这就等价于求解
这个 同余方程,于是 \(\operatorname {exgcd}\) 求解即可
矩阵乘法 记得清空答案矩阵
#include <bits/stdc++.h>
const int MAXN = 105;
const int MOD = 998244353;
using namespace std;
struct Matrix {} I, A;
inline Matrix Qpow (Matrix a, int b);
inline int Qpow (int a, int b, const int p);
inline int BSGS (const int a, const int b, const int p);
inline int EXGCD (const int a, const int b, int &x, int &y);
int N, M, D, K;
int Ans, Tmp;
int B[MAXN];
int main () {
cin >> K;
I.Init (K, 1), A.Init (K, 0);
for (int i = 1; i <= K; ++ i) cin >> B[i];
cin >> N >> M;
for (int i = 1; i <= K; ++ i) A.A[K - i + 1][K] = B[i];
for (int i = 1; i < K; ++ i) A.A[i + 1][i] = 1;
M = BSGS (3, M, MOD), A = Qpow (A, N - K);
D = EXGCD (A.A[K][K], MOD - 1, Ans, Tmp);
if (M % D != 0) return cout << -1 << '\n', 0;
Ans = 1ll * Ans * (M / D) % (MOD - 1), Ans = (Ans + MOD - 1) % (MOD - 1);
cout << Qpow (3, Ans, MOD) << '\n';
return 0;
}
注意模数是 \(p\) 还是 \(\varphi (p)\),完整代码
2. 扩展大步小步算法
\(ex BSGS\),显然我们又要扩展 \(a, p\) 不互质 的部分了
这里用 从已知推未知 的思路,即考虑把 \(a, p\) 从 不互质 的情况变成 互质的情况
设 \(d = \gcd (a, p)\),于是有
这里如果 \(d \nmid b\),则 该方程无解
由于 \(\dfrac a d\) 与 \(\dfrac p d\) 一定 互质,故 \(\dfrac a d\) 在模 \(\dfrac p d\) 意义下 一定有逆元 \(\left ( \dfrac a d \right) ^ {-1}\) ,可以 乘过去
此时 \(a\) 与 \(\dfrac p d\) 并不一定互质,于是我们 继续进行上述操作,直到 \(a \perp p\)
容易证明这样的 操作次数 至多为 \(O (\log p)\) 次,因为 每次消除一个公因数
我们认为 操作了 \(k\) 次 后左边变成了 \(a ^ {x - k}\),此时若 \(b = 1\),则要求的 \(x\) 解就是 \(k\),需求特判
显然 \(a ^ 0 \equiv 1\)
时间复杂度 \(O (\sqrt p + \log ^ 2 p)\),前半部分是 \(BSGS\),后半部分是 转化到互质 的过程
有 \(O (\log p)\) 次 除公因数 过程,每次需要 \(\operatorname {exgcd}\) 求一个 逆元
Luogu P4195 【模板】扩展 BSGS/exBSGS
板,注意 \(IO\) 时间
#include <bits/stdc++.h>
using namespace std;
inline long long EXGCD (const long long a, const long long b, long long &x, long long &y) {
if (b == 0) return x = 1, y = 0, a;
long long d = EXGCD (b, a % b, y, x);
y -= a / b * x; return d;
}
inline long long Inv (const long long a, const long long p) {
long long x, y;
EXGCD (a, p, x, y), x = (x + p) % p;
return x;
}
inline long long Qpow (long long a, long long b, const long long p) {
long long Ret = 1;
while (b) {
if (b & 1) Ret = Ret * a % p;
a = a * a % p, b >>= 1;
}
return Ret;
}
inline long long BSGS (const long long a, const long long b, const long long p) {
static std::unordered_map <long long, long long> Vis; Vis.clear ();
long long B = sqrt (p) + 1, P = Qpow (a, B, p), K = 1, Ans = p;
for (int i = 1; i <= B; ++ i)
K = K * P % p, (! Vis[K]) ? Vis[K] = i : 0;
K = b;
for (int i = 0; i <= B; ++ i) {
if (Vis.count (K)) Ans = min (Ans, Vis[K] * B - i);
K = K * a % p;
}
if (a % p == 0) return b % p == 0 ? 0 : -1;
return Ans == p ? -1 : Ans;
}
inline long long EXBSGS (long long a, long long b, long long p) {
a = a % p, b = b % p;
long long D = __gcd (a, p), K = 0;
while (D > 1) {
if (b == 1) return K;
if (b % D) return -1;
p /= D, b = (b / D) * Inv (a / D, p) % p;
D = __gcd (a %= p, p), ++ K;
}
long long Ret = BSGS (a, b, p);
return Ret != -1 ? (Ret + K) : -1;
}
long long a, b, p, q;
int main () {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
while (cin >> a >> p >> b) {
if (a == 0 && b == 0 && p == 0) break ;
cout << (((q = EXBSGS (a, b, p)) == -1) ? "No Solution" : to_string (q)) << '\n';
}
return 0;
}
EXP - 1 - SP3105 MOD - Power Modulo Inverted
Luogu P5345 【XR-1】快乐肥宅
依托构式,具体细节见代码,此处讲的可能不完备
存在 \(n\) 个 同余方程组 形如
\[k_i ^ x \equiv b_i \pmod {p_i} \]试求解 \(x\) 或 报告无解
容易想到,解 有三种情况,即 无解,唯一解,和 无穷解
若任意一个方程 无解,显然 整个方程组无解,退出程序
若任意一个方程 唯一解,则只需判断 是否所有方程均满足该解,根据情况 输出该解或无解
于是我们尝试判断 方程的解属于哪种情况,我们设 \(f_j = k_i ^ j \pmod {p_i}\)
可以说明,\(f_j\) 呈 \(\rho\) 形分布
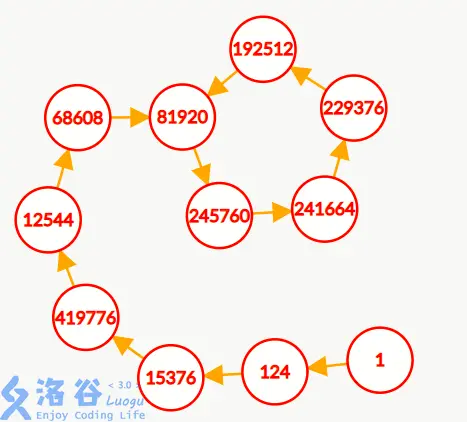
如图是 \(k_i = 124, p_i = 495616\) 的情况,来源 [1] —— 小粉兔
其中 尾巴部分 显然只有 唯一解,这对应我们 \(exBSGS\) 中 不断除去 \(a, p\) 公因数的过程
也就是若在此过程中,出现了 \(b = 1\) 从而得出解,则此解是该方程的 唯一解
证明需要用到 阶 的性质
我们称满足 \(a ^ x \equiv 1 \pmod p\) 的 最小正整数 \(x\) 为 \(a \bmod p\) 的 阶
而 阶 当且仅当 \(a \perp p\) 时 存在,而在 上述过程中,显然 \(a, p\) 并不互质
故不存在使得 \(a ^ x \equiv 1 \pmod p\) 的 正整数,故仅有 唯一解 \(x' = 0\)(即 \(x = k\))
而 在此过程之后,存在 \(a \perp p\),故若 \(BSGS\) 有解,则 原方程一定有无穷解,反之 原方程无解
容易证明,此时 通解 的 “循环节”(即 环长)就是 此时 \(a \bmod p\) 的 阶 \(g\),微调 \(BSGS\) 可求得
\(BSGS\) 求出 特解 使得 \(a ^ {x'} \equiv b_i \pmod p\),显然右式乘上 \(1\) 仍然成立
故环长即是使得 \(a ^ x \equiv 1 \pmod p\) 的 最小正整数 \(x\),即 \(a \bmod p\) 的 阶
微调 \(BSGS\) 目的是 不让其返回 \(0\)(\(a ^ 0 \equiv 1\))
于是我们就将原式 \(k_i ^ x \equiv b_i \pmod {p_i}\) 转化成了 \(x \equiv x'_i \pmod {g_i}\),一个 线性同余方程
之后 \(exCRT\) 即可,但是 模数会爆,我们需要在 模数大于 \(10 ^ 9\) 时 进行特判
如果下一个线性方程 符合当前答案,跳过
反之一定会使得 答案大于当前模数,即 答案大于 \(10 ^ 9\),报告无解
就结束了,代码细节一大堆
#include <bits/stdc++.h>
const int MAXN = 100005;
using namespace std;
inline long long EXGCD (const long long a, const long long b, long long &x, long long &y) {
if (b == 0) return x = 1, y = 0, a;
long long d = EXGCD (b, a % b, y, x);
y -= a / b * x; return d;
}
inline long long Inv (const long long a, const long long p) {
long long x, y;
EXGCD (a, p, x, y), x = (x + p) % p;
return x;
}
inline long long Qpow (long long a, long long b, const long long p) {
long long Ret = 1;
while (b) {
if (b & 1) Ret = Ret * a % p;
a = a * a % p, b >>= 1;
}
return Ret;
}
inline long long BSGS (const long long a, const long long b, const long long p) {
static std::unordered_map <long long, long long> Vis; Vis.clear ();
long long B = sqrt (p) + 1, P = Qpow (a, B, p), K = 1, Ans = p;
for (int i = 1; i <= B; ++ i)
K = K * P % p, (! Vis[K]) ? Vis[K] = i : 0;
K = b;
for (int i = 0; i < B; ++ i) { // ATTENTION : i = B -> Ans = 0, So replace i <= B with i < B
if (Vis.count (K)) Ans = min (Ans, Vis[K] * B - i);
K = K * a % p;
}
if (a % p == 0) return b % p == 0 ? 1 : -1;
return Ans == p ? -1 : Ans;
}
struct Node {
long long p, g; // ATTENTION : Special result (Min result) and Circle Length
} Q[MAXN];
inline Node EXBSGS (long long a, long long b, long long p) {
if (p == 1) return {0, 1}; // ATTENTION
a = a % p, b = b % p;
long long D = __gcd (a, p), K = 0;
while (D > 1) {
if (b == 1) return {K, -1}; // ATTENTION : the ONLY result
if (b % D) return {-1, -1};
p /= D, b = (b / D) * Inv (a / D, p) % p;
D = __gcd (a %= p, p), ++ K;
}
long long Ret = BSGS (a, b, p), Gen = BSGS (a, 1, p);
if (Ret == -1) return {-1, -1};
else return {Ret % Gen + K, Gen};
}
long long A[MAXN], B[MAXN], P[MAXN];
long long Max = 0;
inline long long EXCRT (const Node * T, const int N) {
long long Gcds = 1, RestDis = 0, AnsMul = 0, AnsMod = 0, x, y, AllDiv = T[1].g, AllRes = T[1].p;
for (int i = 2; i <= N; ++ i) {
if (AllDiv > 1e9) { // ATTENTION : If the Mod Bigger than 1e9
if ((AllRes % T[i].g) == (T[i].p % T[i].g)) continue ;
else exit ((cout << "Impossible" << '\n', 0));
}
Gcds = EXGCD (AllDiv, T[i].g, x, y), RestDis = ((- AllRes + T[i].p) % T[i].g + T[i].g) % T[i].g;
if (RestDis % Gcds) exit ((cout << "Impossible" << '\n', 0));
AnsMul = RestDis / Gcds, AnsMod = T[i].g / Gcds;
x = x * AnsMul % AnsMod, y = y * AnsMul % AnsMod;
AllRes = (AllRes + x * AllDiv), AllDiv = AllDiv * AnsMod, AllRes = (AllRes % AllDiv + AllDiv) % AllDiv;
}
if (AllRes < Max) AllRes += ((Max - AllRes - 1) / AllDiv + 1) * AllDiv; // ATTENTION
if (AllRes > 1e9) exit ((cout << "Impossible" << '\n', 0));
return AllRes;
}
int N, X = -1;
inline void Check (const long long x) {
for (int i = 1; i <= N; ++ i)
if (Qpow (A[i], x, P[i]) != B[i])
exit ((cout << "Impossible" << '\n', 0));
exit ((cout << x << '\n', 0));
}
int main () {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> N;
for (int i = 1; i <= N; ++ i) {
cin >> A[i] >> P[i] >> B[i];
Q[i] = EXBSGS (A[i], B[i], P[i]);
if (Q[i].p == -1) return cout << "Impossible" << '\n', 0;
if (Q[i].g == -1) X = Q[i].p;
Max = max (Max, Q[i].p);
}
if (~ X) Check (X); // ATTENTION : ONLY result Check, Must After All Input
// for (int i = 1; i <= N; ++ i)
// cerr << "Rest : " << Q[i].p << " Mod : " << Q[i].g << '\n';
cout << EXCRT (Q, N) << '\n';
return 0;
}

