素数

素数

即 质数，巨大多内容板块

此处获取本节调试数据 / 代码包

全文 绝大多数 内容是对 [0] 中讲述的 粗略抄写 和 胡乱加工

1. 基本概念

定义

如果数 \(p\) 有且仅有 \(1\) 和 \(p\) 两个因子，这个数就是 素数（质数）

反之即为 合数，显然，每个 \(>1\) 的整数要么是 素数，要么是 合数

特别的，规定 \(1\) 既不是素数，也不是合数

性质

1. 任何 正整数 \(n\) 均可表示为 若干素数 的 乘积

   根据定义容易证明，若一个数 有多个因数，可将其 分解为若干因数的乘积

   直到分解到 每个因数均不可再分解，此时的每个因数 即为素数

2. 算术基本定理：正整数 \(n\) 有且仅有 一种 分解成 若干素数乘积 的方式（不记顺序）

   考虑 反证法，若存在数 \(n\) 有 至少两种 分解方式，且 \(n\) 是 最小的 这样的数

   即 \(n = \prod p ^ {a} = \prod q ^ b ~ (\exists ~p \neq q)\)

   显然，\(p_1 \mid \prod q ^ b\)，则 \(q_1, q_2, ..., q_m\) 中至少存在一个 \(q_i\) 使得 \(p_1 \mid q_i\)

   不妨设 \(q_i\) 就是 \(q_1\)，于是 \(p_1 \mid q_1\)，又知道 \(p, q\) 均为 素数，故 \(p = q\)

   而若 \(a_1 > b_1\)，则 \(p_1 ^ {a_1 - b_1} \times p_2 ^ {a_2} \times ... \times p_n ^ {a_n} = q_2 ^ {b_2} \times q_3 ^ {b_3} \times ... \times q_n ^ {b_n}\)

   于是 \(q_2, q_3, ..., q_m\) 中至少存在一个 \(q_i\) 使得 \(p_1 \mid q_i\)，但 \(p_1 = q_1 \neq q_i ~ (i \in [2, m])\)

   故矛盾，同理当 \(a_1 < b_1\) 时 亦矛盾，则仅有 \(a_1 = b_1\) 这种可能

   于是 \(n' = \prod \limits _ {i = 1} ^ n p_i ^ {a_i} = \prod \limits _ {i = 1} ^ m q_i ^ {b_i}\)，我们可以将上述过程 推广到 \(n, m\) 来证明

   但其实由于我们 认为 \(n\) 是 最小的 这样的数，但显然 \(n' < n\)，故 矛盾

   则 原命题已经得证

3. 第 \(n\) 个 素数 \(P_n\) 大致大小为 自然对数 的 \(n\) 倍，即 \(P_n \sim n \ln n\)

4. 大小不超过 \(x\) 的 素数个数 \(\pi (x) \sim \dfrac x {\ln x}\)

   \(3./4.\) 的 证明十分的硬，此处不表

梅森数

和 素数 有些关系，梅森数 是 形如

\[2 ^ p - 1 \]

的数，其中 \(p\) 是 素数

显然，当 \(p\) 为 合数 时，\(2 ^ p - 1\) 一定 不是素数，因为其至少有 \(2 ^ m - 1\) 这个因子

\[2 ^ {km} - 1 = (2 ^ m - 1) (2 ^ {m (k - 1)} + 2 ^ {m (k - 2)} + ... + 1) \]

但当 \(p\) 为 素数 时，\(2 ^ p - 1\) 并 不一定是素数，例如 \(2 ^ {11} - 1 = 2047 = 23 \times 89\) 就假了

2. 互素关系

定义

当 \(\gcd (n, m) = 1 ~ (n, m \in \mathbb Z)\) 时，我们就称它们是 互素（互质）的

\[n, m \in \mathbb Z, \gcd (n, m) = 1 \Longleftrightarrow n \perp m \]

\(Stern-Brocot\) 树

可以用于构造所有 最简分数（\(\dfrac m n ~ (m \perp n)\)）的集合

其核心操作 十分简单，考虑从 \((\dfrac 0 1, \dfrac 1 0)\) 两个分数出发，重复若干次 下面这个操作

• 向 相邻两分数 \(\dfrac m n, \dfrac {m'} {n'} ~ (\dfrac m n < \dfrac {m'} {n'})\) 之间插入 \(\dfrac {m + m'} {n + n'}\) 这个 “中位分数”

这里就 忽略分母为 \(0\) 这个问题 了

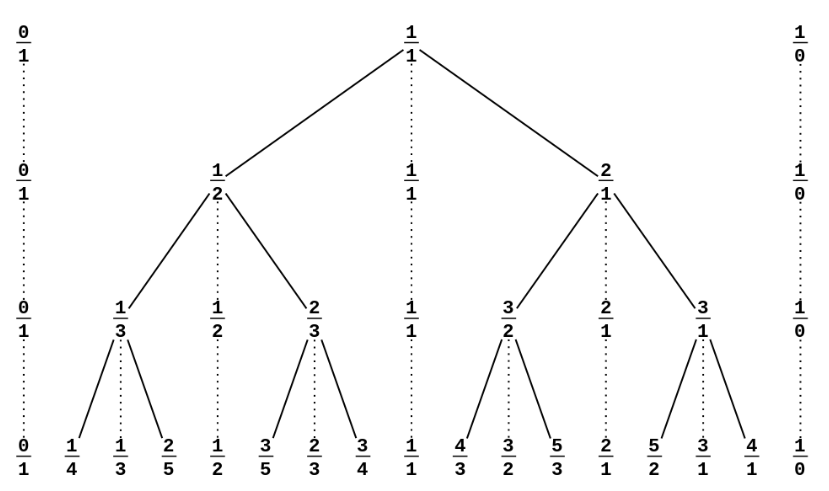
图片来源于 [1]

这相当于 一棵无尽的二叉树，我们 构造的序列 即是其 中序遍历 得到的序列

其中 每一个结点都代表一个分数，每一个分数都可以表示成 \(\dfrac {m + m'} {n + n'}\) 的 形式

其中 \(\dfrac m n\) 是 在它左边离它最近的祖先，\(\dfrac {m'} {n'}\) 是 在它右边离它最近的祖先

如何证明这种构造能 不重不漏的 得到 所有的 最简分数 呢？

首先，根据我们 小学奥数 中的 糖水原理，容易证明 两分数 生成的 中位分数 满足

\[\dfrac m n < \dfrac {m + m'} {n + n'} < \dfrac {m'} {n'} \]

故 不可能重复，而 由于我们每次生成的数 均严格在两数之间，故 每次递归区间变小

容易理解，当 无尽的递归下去，区间将变得 充分小，不会漏掉

同理，它应当能得到 所有的 符合条件的数，我们只需论证为什么其得到的一定是 最简分数

先考虑来证明一个 引理

若 \(ad - bc = 1\)，则 \(a \perp b, c \perp d\)（\(a, b, c, d \in \mathbb Z\)）

仍然考虑反证，若存在 \(\gcd (a, b) = k > 1\)，则有 \(a = ka', b = kb'\)

于是 \(k a'd - k b'c = 1\)，即 \(k (a'd - b'c) = 1\)，又 \(k > 1, a, b, c, d \in \mathbb Z\)，显然矛盾

故 \(\gcd (a, b) = 1\)，即 \(a \perp b\)，而 \(c, d\) 与 \(a, b\) 显然对称，故原命题得证

根据上述引理，我们容易推导出，若 \(mn' - m'n = 1\)，则 \(\dfrac m n, \dfrac {m'} {n'}\) 为 最简分数

即 \(n \perp m, n' \perp m'\)

于是我们只需论证 对于序列上任意相邻两数，均满足 \(mn' - m'n = 1\) 即可

显然 \(\dfrac 0 1, \dfrac 1 0\) 满足该性质，于是我们可以考虑 向下递推

设有 \(\dfrac m n, \dfrac {m'} {n'}\) 已满足条件，我们只需证明 \(\dfrac m n, \dfrac {m' + m} {n' + n}\) 与 \(\dfrac {m' + m} {n' + n}, \dfrac {m'} {n'}\) 均满足条件即可

于是有 \(m (n' + n) - n (m' + m) = (m' + m) n' - (n' + n) m' = mn' - m'n = 1\)

故原命题得证，即 核心操作 得到的一定是 最简分数

\(Farey\) 序列

与 \(Stern-Brocot\) 树 相辅相成，互相统一，我们将第 \(i\) 个 \(Farey\) 序列记作 \(F_i\)

\(Farey\) 序列，即 法里序列，也有称 \(F_i\) 为 阶为 \(i\) 的法里级数 的说法，本质相同

其表示 分母小于等于 \(i\) 的 最简真分数 按 从小到大 顺序排列形成的集合

图片来源于 [1]

容易发现，每个 \(Farey\) 序列就是 \(Stern-Brocot\) 的 一棵子树，故 构造是简单的

且显然的性质是，对于序列中任意 连续的三个数 \(\dfrac a b, \dfrac c d, \dfrac e f\)，其满足 \(c = a + e, d = b + f\)

Luogu P8058 [BalkanOI2003] Farey 序列

求第 \(n\) 个 \(Farey\) 序列中的第 \(k\) 项

这里提供一种不同于 [0] 中的做法，复杂度 \(O (N \log V)\)，参考 [2]

考虑直接构造复杂度是 \(O (N ^ 2)\) 的，不可承受

注意到 \(Farey\) 序列具有 单调性，容易想到 二分答案 \(x\)

于是我们只需要求在第 \(N\) 个 \(Farey\) 序列上，小于 \(x\) 的分数有多少个即可，记这个个数为 \(W\)

由 \(Farey\) 序列的定义，容易知道二分 上下界 \(x \in [0, 1], x \in \Q\)

我们定义 \(f_i\) 为 小于 \(x\) 的 分数 个数，当 不要求最简 时，显然 \(f_i = \lfloor ix \rfloor\)

若我们 要求最简，则容易得出 \(f_i = \lfloor ix \rfloor - \sum \limits _ {d \mid i} f_d\)，而 \(W = \sum \limits _ {i = 1} ^ n f_i\)

由于每次求和均从 \(1\) 到 \(n\)，故后面这部分可以 \(O (N \log N)\) 预处理系数（筛一下）

然后就结束力，预处理后 二分单次 \(Check\) 可以做到 \(O (N)\)，故总复杂度 \(O (N (\log V + \log N))\)

#include <bits/stdc++.h>

const int MAXN = 40005;
const double EPS  = 1e-10;

using namespace std;

int F[MAXN], C[MAXN];

int N, K;

inline void Init () {
	for (int i = 1; i <= N; ++ i) C[i] = 1;
	for (int i = N; i >= 1; -- i)
		for (int j = i * 2; j <= N; j += i)
			C[i] -= C[j];
}

inline bool Check (const double M) {
	int Cnt = 0;
	for (int i = 1; i <= N; ++ i) Cnt += int (M * i) * C[i];
	return Cnt < K;
}

inline void Solve (const double x) {
	int Ans;
	for (int i = 1; i <= N; ++ i) {
		Ans = ceil (i * x);
		if (fabs (1.0 * Ans / i - x) <= EPS)
			return cout << Ans << ' ' << i << '\n', void ();
	}
}

double L = 0, R = 1, M, A;

int main () {
	
	cin >> N >> K;
	
	Init ();
	
	while (R - L >= EPS) {
		M = (L + R) / 2;
		if (Check (M)) L = A = M;
		else R = M;
	}
	
	Solve (A);
	
	return 0;
}

[ABC333G] Nearest Fraction

双倍经验 Luogu P1298 最接近的分数 但是可以暴力过掉，注意多 判断分子

调了半天，就不应该尝试 卡精度，老老实实用 __int128 和 分数类 就行了

这个题又 完全不卡时间

思路是 简单的，就是在 \(Stern-Brocot\) 树上二分

但是如果直接 暴力一层一层地跳，就会 \(TLE / RE\) 掉（\(RE\) 是因为 递归层数过多）

比如 \(1e-18\) 这个数，就是 一直向左跳，而每次分母只增加 \(1\)，就会挂掉

故考虑 倍增，每次尝试往 一个方向跳到底 再换方向跳

考虑 \(Stern-Brocot\) 树的性质，一个结点 由 左右离他最近的祖先 分子分母 分别求和得到

容易发现，每次换向，分母就会变成 其父亲和其父亲的父亲 的和，成 \(Fib\) 数列

故可以证明，这样的换向应当是 \(O (\log N)\) 次的（分母最大为 \(N\)）

加上倍增，总时间复杂度就是 \(O (\log ^ 2 N)\)，甚至 可以多组询问

#include <bits/stdc++.h>

const __int128 INF = 10000000000000000000ull;

using namespace std;

struct Fract {
	__int128 x, y;
	
	inline Fract operator + (const Fract &a) const {
		return {x + a.x, y + a.y};
	}
	
	inline Fract operator - (const Fract &a) const {
		return {x * a.y - a.x * y, y * a.y};
	}
	
	inline bool operator < (const Fract &a) const {
		return x * a.y < y * a.x;
	}
	
	inline bool operator > (const Fract &a) const {
		return x * a.y > y * a.x;
	}
	
	inline __float128 Val () const {
		return (__float128) 1.0 * x / y;
	}
};

long long N;

inline Fract Mul (const Fract &a, const long long x) {
	return {a.x * x, a.y * x};
}

inline Fract ABS (const Fract &a) {
	if ((a.x > 0 && a.y < 0) || (a.x < 0 && a.y > 0)) return {- a.x, a.y};
	return {a.x, a.y};
}

inline Fract Que (const Fract val, Fract L = {0, 1}, Fract R = {1, 0}) {
	Fract M = L + R, l = L, r = R, x, y;
	
	while (1) {
		M = L + R, x = R;
		
		if (M.y > N) return ABS (L - val) > ABS (R - val) ? R : L;
		
		for (int i = 33; ~ i; -- i) {
			y = x, x = x + Mul (L, 1ll << i);
			if (x.y > N || x < val) x = y; 
		}
		
		r = x, x = L;
		
		for (int i = 33; ~ i; -- i) {
			y = x, x = x + Mul (R, 1ll << i);
			if (x.y > N || x > val) x = y;
		}
		
		l = x, L = l, R = r;
	}
}

Fract val;

long double v;

int main () {
	
	cin >> v >> N;
	
	val = {(unsigned long long) (v * INF), INF};
	
	Fract Ans = Que (val);
	
	cout << (unsigned long long) Ans.x << ' ' << (unsigned long long) Ans.y << '\n';
	
	return 0;
}

SP26073 DIVCNT1 - Counting Divisors

定义 \(d (n)\) 为 \(n\) 的 正整数因数个数，多次询问 \(\sum \limits _ {i = 1} ^ {n} d (i)\)

下文中部分 图片 / 思路 来源于 [3]

先考虑 对式子转化，令 \(B = \left \lfloor \sqrt N \right \rfloor\)，于是有

\[\begin {aligned} & \sum \limits _ {i = 1} ^ {n} { d(i) } \\ =& \sum \limits _ {i = 1} ^ {n} { \left \lfloor \dfrac n i \right \rfloor } \\ =& \sum \limits _ {i = 1} ^ {n} { \sum \limits _ {j = 1} ^ {n} { \left [ i \times j \le n \right ] } } \\ =& \sum \limits _ {i = 1} ^ {B} { \sum \limits _ {j = 1} ^ {n} { \left [ i \times j \le n \right ] } } + \sum \limits _ {i = 1} ^ {n} { \sum \limits _ {j = 1} ^ {B} { \left [ i \times j \le n \right ] } } + \sum \limits _ {i = B + 1} ^ {n} { \sum \limits _ {j = B + 1} ^ {n} { \left [ i \times j \le n \right ] } } - \sum \limits _ {i = 1} ^ {B} { \sum \limits _ {j = 1} ^ {B} { \left [ i \times j \le n \right ] } } \\ =& \sum \limits _ {i = 1} ^ {B} { \sum \limits _ {j = 1} ^ {n} { \left [ i \times j \le n \right ] } } + \sum \limits _ {i = 1} ^ {n} { \sum \limits _ {j = 1} ^ {B} { \left [ i \times j \le n \right ] } } - \sum \limits _ {i = 1} ^ {B} { \sum \limits _ {j = 1} ^ {B} { \left [ i \times j \le n \right ] } } \\ =& 2 \sum \limits _ {i = 1} ^ {B} { \left \lfloor \dfrac n i \right \rfloor } - B ^ 2 \end {aligned} \]

我们要求的就是 \(\sum \limits _ {i = 1} ^ B {\left \lfloor \dfrac n i \right \rfloor}\)，相当于 反比例函数 \(y = \dfrac n x\) 内侧，在 \(y \in [1, B]\) 段的 整点数

直接做是 \(O (B)\) 的，多组询问，似得很透彻

考虑用一些 很新的方式 来数这个整点，比如尝试用 一些向量 来 拟合 这个 反比例函数

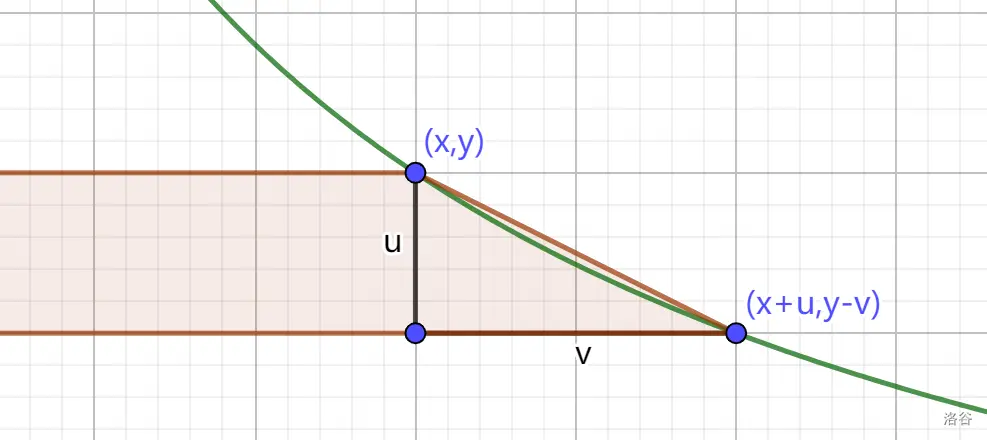
容易发现，对于反比例函数上一点，斜率最接近该点导数 的 整向量 \((u, v)\)（向量两端点均为整点）

若保证 一端点为该点，另一端点在 反比例函数外侧

靠反比例函数内侧 包含且仅包含了 反比例函数内侧 所有整点（见上图）

于是我们不断地 构造这样最贴近的向量 即可

先考虑 一个这样的向量 带来的贡献，显然就是 一个矩形 和 一个三角形

于是贡献为 \(x v + \dfrac {(u - 1) (v + 1)} {2}\)

可以认为 最上方一列 算成 上面一个向量的贡献，不能重复计算，故第一部分不是 \(x (v + 1)\)

现在只需要考虑 构造 的方法了，显然，我们应当按照如下的 大致思路

1. 选定 起始点 和 起始斜率
2. 不断 递增斜率，找到 最贴近当前点 \((x, y)\) 的向量
3. 将当前点 移动到 选中向量的右端
4. 重复上述步骤直到 终点

分步考虑，选定起点 显然 十分的简单，对于一个 反比例函数，我们需求 \(y \in [1, B]\) 的部分

于是起始 \(x = y = B\) 即可，斜率 显然就是 \(- B\)

为了 不漏算，显然最后我们拟合的图像上的整点 均不在原反比例函数内侧

故具体而言，此处起点 \(x = \left \lfloor \dfrac n B \right \rfloor, y = B + 1\)，而 为了方便，斜率均采用 绝对值后的值

中间两步是 重点，对于 当前点 和 当前向量，为了 贴近原函数

显然我们先 执行多次 \(3.\) 操作，直到 下一次移动会使当前点移动到原函数内侧

这时候开始找 新的向量，我们可以使用一个 单调栈 来维护 斜率递减的向量集

这里的 斜率 是 绝对值后的，故称为 递减

我们每次 取出栈顶，若该线段 仍会使得下一次移动后当前点到原函数内侧，则 将其弹出

于是我们最终能找到 两条向量，使得其另一端 恰好跨过原函数两侧，如下图

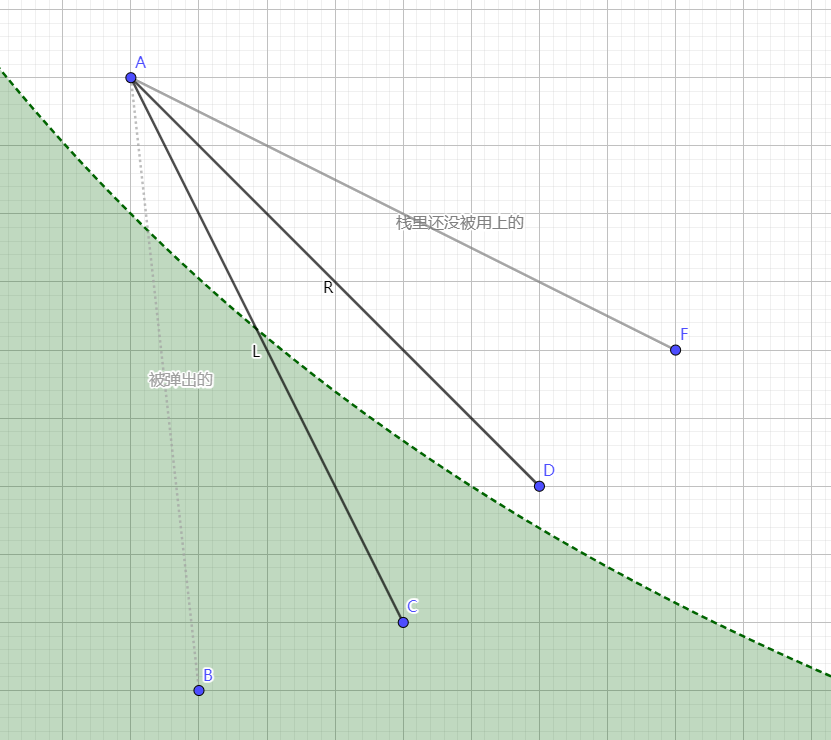
接着我们就可以 依据这两个向量，来找到最贴近 **原函数 **的 新向量 了

考虑用 \(Stern-Brocot\) 树 的 构造方式，得到向量 \(M = (L_x + R_x, L_y + R_y)\)

容易发现，若从 当前点 起始，向量 \(M\) 的 另一端 在 原函数外侧

则我们可以 弹出 \(R\)，加入 \(M\)，重复找 \(M\) 的上述操作

反之我们 弹出 \(L\)，加入 \(M\)，重复找 \(M\) 的上述操作

考虑 什么时候终止 呢？如果 \(R\) 的斜率 大于 原函数在 \(x + x_L\) 点的斜率

显然无论如何分下去，我们都 不可能再得到 一个 \(M\) 使得其另一端在原函数外侧了

显然 \(L\) 另一端在内侧，而 \(R\) 斜率比 原函数 在 \(L\) 另一端斜率 大

故加上 \(R\) 后得到的 \(M\) 只会 在原函数内侧，离原函数更远（相较于 \(L\)）

这时候我们就 停止二分，而 最后一次合法的 \(M\) 就是我们想要的

这一部分可以 配合上图理解

最后我们需要来考虑一下 终点 的问题

考虑到 后期函数斜率很小，基本都会是 \(\dfrac 1 k\) 的形式，相当于 \(Stern-Brocot\) 上 最靠右的几列

容易发现，此时 层数 与 \(k\) 十分接近，即 二分 这一步的 时间复杂度 将退化到 \(O (k)\)

或说 \(O (y)\)

不太可承受，于是考虑 这一部分可以直接暴力做掉，而 这一部分 我们取 \(O (\sqrt [3] n)\)

据可靠消息，这样询问一次时间复杂度就是 \(O (\sqrt [3] {n} \log n)\) 的

据可靠消息 的意思就是 笔者不会证明

然后再看一下这个 原题 的数据范围

完全能过

注意各种 long long 和大量 __int128 的使用，记得重载输出

#include <bits/stdc++.h>

const int MAXN = 100005;

using namespace std;

int T;

struct Writer {
    template <typename T> Writer& operator << (T x) {
        if (x == 0) { putchar('0'); return *this; }
        if (x <  0) putchar('-'), x = -x;
        static short sta[40], top = 0;
        while (x > 0) sta[++ top] = x % 10, x /= 10;
        while (top > 0) putchar(sta[top] + '0'), top --;
        return *this;
    }
    inline Writer& operator << (char c) {putchar(c); return *this;}
    Writer() {}
} out;

struct Vector {
	int x, y;
	
	inline Vector operator + (const Vector &a) const {
		return {x + a.x, y + a.y};
	}
};

long long N;

inline bool Checkin (const long long x, const long long y) {
	return (__int128) x * y <= N;
}

inline bool Checked (const long long x, const Vector v) {
	return (__int128) N * v.x <= (__int128) v.y * x * x; // Abs
}

vector <Vector> S;

inline void Solve () {
	cin >> N;
	
	long long b = sqrt (N), c = cbrt (N), x = N / b, y = b + 1;
	__int128 Ans = 0;
	Vector L, R, M;
	
	S.push_back ({1, 0}), S.push_back ({1, 1});
	
	while (1) {
		for (L = S.back (), S.pop_back (); !Checkin (x + L.x, y - L.y); x += L.x, y -= L.y)
			Ans += (__int128) x * L.y + (__int128) (L.y + 1) * (L.x - 1) / 2;
		if (y <= c) break ;
		for (R = S.back (); Checkin (x + R.x, y - R.y); S.pop_back (), R = S.back ()) L = R;
		while (1) {
			M = L + R;
			if (!Checkin (x + M.x, y - M.y)) S.push_back (R = M);
			else if (Checked (x + (L = M).x, R)) break ;
		}
	}
	
	for (int i = 1; i < y; ++ i) Ans += N / i;
	out << ((Ans << 1) - (b * b)) << '\n';
}

int main () {
	
	cin >> T;
	
	while (T --) Solve ();
	
	return 0;
}

3. 素数筛法

\(Sieve ~ of ~ Prime\)

十分重要，从 普及 - 到 NOI，许多数论题 都要求处理 \([1, N]\) 的 所有素数

板子 Luogu P3383 【模板】线性筛素数

埃式筛法

\(Sieve ~ of ~ Eratosthenes\)

全称 埃拉托斯特尼筛法，十分经典，时间复杂度 \(O (N \ln \ln N)\)

其核心在于 用已经筛出的素数 的整倍标记 合数，代码就很简单

bool Vis[];

inline void Prime (const int N, vector <int> &Pri) {
	for (int i = 2; i <= N; ++ i) 
		if (!Vis[i]) {
			Pri.push_back (i);
			for (int k = i; k <= N; k += i)
				Vis[k] = 1;
		}
}

比较 精妙 的点在于其 复杂度的证明，即 \(\sum \limits _ {p \in \mathbb P, p \le n} \dfrac n p = O (n \ln \ln n)\)

注意到 每个数会被它 所有质因数 筛到一遍，故可以有

以下证明 来自 djq 老师，并不保证经过笔者理解或验证

\[\begin {aligned} \sum \limits _ {p \in \mathbb P, p \le n} \dfrac n p =& \sum \limits _ {i = 1} ^ {n} \omega (i) \end {aligned} \]

根据 \(d (i)\) 的计算式有

\[\begin {aligned} \sum \limits _ {i = 1} ^ {n} { 2 ^ {\omega (i)} } \le& \sum \limits _ {i = 1} ^ {n} { d (i) } = O (n \ln n) \end {aligned} \]

根据 \(2 ^ x\) 的 凸性 和 琴生不等式 有

\[\begin {aligned} \sum \limits _ {i = 1} ^ {n} { 2 ^ {\omega (i)} } \ge & 2 ^ { \frac { \sum _ {i = 1} ^ {n} { \omega (i) } } {n} } n \\ \therefore { 2 ^ { \frac { \sum _ {i = 1} ^ {n} { \omega (i) } } {n} } } \le & O (\ln n) \end {aligned} \]

于是两边 同时取对数，有

\[\begin {aligned} \frac { \sum _ {i = 1} ^ {n} { \omega (i) } } {n} \le & O (\log \ln n) \\ \therefore \sum \limits _ {i = 1} ^ {n} { \omega (i) } =& O (n \log \ln n) = O (n \log \log n) = O (n \ln \ln n) \end {aligned} \]

这已经很快了，但是 不够快，它甚至 卡不过去板子（真的不是因为板子是 线性筛 吗？

于是注意到下列优化（

1. 我们其实只需要 筛到根号，于是

   bool Vis[];
   
   inline void Prime (const int N, vector <int> &Pri) {
   	for (int i = 2; i * i <= N; ++ i) 
   		if (!Vis[i]) 
   			for (int k = (i << 1); k <= N; k += i)
   				Vis[k] = 1;
   	for (int i = 2; i <= N; ++ i)
   		if (!Vis[i]) Pri.push_back (i);
   }
   

2. 第二重循环，可以从 \(i ^ 2\) 开始，因为更小的前面已经筛过了

   bool Vis[];
   
   inline void Prime (const int N, vector <int> &Pri) {
   	for (int i = 2; i * i <= N; ++ i) 
   		if (!Vis[i]) 
   			for (int k = i * i; k <= N; k += i)
   				Vis[k] = 1;
   	for (int i = 2; i <= N; ++ i)
   		if (!Vis[i]) Pri.push_back (i);
   }
   

3. 提前筛出 偶数，然后第二重循环可以 成倍加

bool Vis[];

inline void Prime (const int N, vector <int> &Pri) {
	for (int i = 4; i <= N; i += 2) Vis[i] = 1;
	for (int i = 3; i * i <= N; ++ i) 
		if (!Vis[i]) 
			for (int k = i * i; k <= N; k += (i << 1))
				Vis[k] = 1;
	for (int i = 2; i <= N; ++ i)
		if (!Vis[i]) Pri.push_back (i);
}

上述方法任选，均可通过板子

欧拉筛法

\(Sieve ~ of ~ Euler\)

其本质仍然是 用质数标合数，但是在 埃式筛 中，一个合数可能会被 多个质数 筛到

这就造成了 非线性的复杂度，而在 欧拉筛 中，我们可以保证 一个合数只被筛到一次

这样就保证了复杂度

具体而言，我们尝试 只用每个合数的最小质因数 筛掉它

于是我们对于每个 \(i\)，从小到大 遍历 已知质数 \(p_j\)，并标记合数 \(i \times p_j\)

当 \(p_j \mid i\) 时，停止遍历，由于我们 从小到大 遍历的质数，故此时 \(p_j\) 一定是 \(i\) 的 最小质因子

复杂度 \(O(n)\)，十分正确

bool Vis[];

inline void Prime (const int N, vector <int> &Pri) {
	for (int i = 2; i <= N; ++ i) {
		if (!Vis[i]) Pri.push_back (i);
		for (auto k : Pri) {
			if (i * k >  N) break ;
			Vis[i * k] = 1;
			if (i % k == 0) break ;
		}
	}
}

4. 素性测试

试除法

容易发现，我们尝试 \(2 \sim \sqrt N\) 之间有没有整数 整除 \(N\) 即可

费马素性测试

基于 费马小定理，若 \(n \in \mathbb P, a \perp N\)，则有 \(a ^ {n - 1} \equiv 1 \pmod n\)

于是 随机选一些 \(a \in [1, n)\)，但 无需保证 \(a \perp n\)，根据上述定理判断

• 若 \(a ^ {n - 1} \equiv 1 \pmod n\) 不成立，则 \(n\) 一定不是素数
• 若 \(a ^ {n - 1} \equiv 1 \pmod n\) 成立，则 \(n\) 大概率 是素数

显然，尝试的 \(a\) 越多，\(n\) 是素数的概率越高，但其始终 不是完全正确的

为什么不用保证 \(a \perp n\)？显然，当 \(n\) 为 素数 是，始终有 \(a \perp n\)，不影响判断

更令人难受的是，有一些合数 \(d\)，无论取什么 \(a \in [1, d)\) 都不能把它判掉

我们称这种数是 \(Carmicgeal\) （卡迈克尔）数，前面几个是 \(561, 1105, 1729, ...\)

它在 \(10 ^ 7\) 的范围内就有 \(255\) 个，根本 特判不掉，这就成了这个素性测试的 致命问题

[4] \(Wiki - pedia\) 上指明，当 \(n\) 充分大时，\([1, n]\) 间有 至少 \(n ^ {\frac 2 7}\) 个 \(Carmicgeal\) 数

\(Miller - Rabin\)

这才是 重点，其在 保证时间复杂度 的情况下 部分解决了 费马素性测试的不完美

此算法（及其优化变种）是 已知最快的（非确定性）素性测试算法

仍然基于 费马素性测试，然后多次进行 二次探测定理逆否命题判定，排除 \(Carmicgeal\) 数

二次探测定理 可以在 同余关系 一部分中找到

具体而言，对于数 \(n\)，我们将 \(n - 1\) 表示成 \(2 ^ t u\) 的形式，其中 \(2 \nmid u\)

我们任取一基数 \(a\)，计算 \(a ^ u \pmod n\) 的值，考虑每次将其 乘方，即得到 \(a ^ {2u} \pmod n\)

根据 二次探测定理，若 \(n \in \mathbb P\)，则 \(x ^ 2 \equiv 1 \pmod n\) 有且仅有 \(x \equiv 1\) 与 \(x \equiv n - 1\) 两解

当每次 \(a ^ {2u} \equiv 1 \pmod n\) 时，去判断是否 \(a ^ u \equiv 1 \pmod n\) 或 \(a ^ u \equiv n - 1\pmod n\) 即可

容易发现，若 \(n \in \mathbb P\)，或 \(n\) 为 \(Carmicgeal\) 数，则至少 \(a ^ {n - 1} \equiv 1 \pmod n\)，且 \(2 \mid n - 1\)

也就是说 对于一个基数 \(a\)，我们 至少可以做一次检测

据理论证明，其每次测试 错误概率 \(< \dfrac 1 4\)，于是 \(50\) 次测试后错误概率只有 \(4 ^ {-50}\)，十分安全

其优势在于 没有 类似于 \(Carmicgeal\) 数 一样的 无法得出正确解 的数

显然，我们对于 选取的基数 \(a\)，需要做 一次快速幂，同时做 \(t\) 次倍增，时间复杂度 \(O (\log N)\)

故总时间复杂度 \(O (k \log N)\)，其中 \(k\) 是 选择的基数个数，这东西 快的很啊

但是吧，非确定性 的算法 总是不那么让人放心，即使其错误率极低

而事实上，该算法初始实质上是一个 基于广义黎曼猜想 的 确定性算法

虽然 猜想没有被证明，但是我们仍能在 一定范围内验证它

从而得到一个 在一定范围内的确定性算法

具体而言，我们给出以下范围选择

在 \(n \le 2 ^ {32}\) 的范围内，可以使用 \(2, 7, 61\) 三个底数，或 前四个质数 作为底数

在 \(n \le 2 ^ {61}\) 的范围内，可以使用 前九个质数 作为底数

在 \(n \le 2 ^ {64}\) 的范围内，可以使用 \(2, 325, 9375, 28189, 450775, 9780504, 1795265022\) 七个底数

在 \(n \le 2 ^ {78}\) 的范围内，可以使用 前十二个质数 作为底数

在 \(n < 2 ^ {81}\) 的范围内，可以使用 前十三个质数 作为底数

于是这下就可以 放心使用了

namespace Miller_Rabin {

	int P[15] = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37};
	int MAX_32 = 4, MAX_61 = 9, MAX_64 = 12;
	
	inline long long Qpow (__int128 a, long long b, const long long p) {
		__int128 Ret = 1;
		while (b) {
			if (b & 1) Ret = Ret * a % p;
			a = a * a % p, b >>= 1;
		}
		return Ret;
	}
	
	inline bool Check (const long long x) {
		if (x < 3 || !(x & 1)) return x == 2;
		long long d = x - 1, t = 0;
		__int128 v;
		while (!(d & 1)) d >>= 1, ++ t;
		for (int i = 0; i < MAX_64 && P[i] < x; ++ i) {
			v = Qpow (P[i], d, x);
			if (v == 1) continue ;
			for (int k = 0; k < t; ++ k) {
				if (v == x - 1) break ;
				v = v * v % x;
				if (k == t - 1) return 0;
			}
		}
		return 1;
	}
}

以上代码有一些 小小的优化，会比较快

1. 对质数 \(2\) 的特判
2. 对于底数 \(a\)，有 \(a ^ u \equiv 1 \pmod n\) 时，显然 \(a ^ {u 2 ^ t} \equiv 1 \pmod n\)，可以提前判定通过
3. 同时当出现 \(a ^ {u 2 ^ t} \equiv n - 1 \pmod n\) 时，当且仅当 \(t = 0\) 时我们 不能直接判定通过

显然若 \(u = n - 1\) 时...

\(AKS\)

抽象算法，目前已经证明的 渐近时间复杂度 \(O (\log ^ {10.5} n)\)

而 变体 可以优化到 \(O (\log ^ 6 n) \sim O (\log ^ {7.5} n)\)（仍然毫无帮助

但其具有 独特地位，因为

它是第一个被发表的 一般的、多项式的、确定性的 和 无仰赖的 素数判定算法

—— [5] 百度百科

实现和证明 可能对于 \(OI\) 并无帮助，过于困难？了，这里只 简单介绍 基本定理

若 \(a \perp p, a \in \mathbb Z\)，则 \(p \in \mathbb P\) 的 充分必要 条件 是

\[\begin {aligned} (x - a) ^ p & \equiv (x ^ p - a) \pmod p \end {aligned} \]

但是由于我们要验证 所有与 \(p\) 互质的 \(a\)，上式不可做，于是有以下的 同余多项式

\[\begin {aligned} (x + a) ^ n & \equiv (x ^ n + 1) \pmod {x ^ r - 1, n} \end {aligned} \]

这等价于存在 多项式 \(f, g\)，使得

\[\begin {aligned} (x + a) ^ n - (x ^ n + a) & = (x ^ r - 1) g + nf \end {aligned} \]

而有关 \(AKS\) 算法的正确性证明中，推导出了一个 足够小的 \(r\)，以及 整数集 \(a \in A\)

只要验证当 \(r\) 为该值时，上式对所有的 \(a \in A\) 均成立，则 \(n\) 为 素数

其中 \(r\) 应当是 最小的 使得 \(n \bmod r\) 的 阶* \(> \log N\) 的 正整数

* : 若 \(n \perp r\)，则称使得 \(n ^ k \equiv 1 \pmod r\) 的 最小正整数 \(k\) 为 \(n \bmod r\) 的 阶

而 \(a \in [1, \left \lfloor \sqrt {\varphi (r)} \log n \right \rfloor]\) 即可，可以证明， \(r\) 与 \(|A|\) 均是 \(poly ~ \log n\) 级别的

5. 分解质因数

试除法

显然的 \(O (\sqrt n)\) 算法，我们在 判定 \(n\) 的素性 的 过程中

每遇到一个 \(a\)，满足 \(a \mid n\)，就 将 \(n\) 除尽 \(a\)，并记录

容易证明 每次找到的 \(a\) 一定是 当前 \(n\) 的 最小质因数

\(Pollard - rho\)

核心思想仍然是 随机

我们知道 生日悖论

也就是 \(O (\sqrt n)\) 次随机内取到至少一组相同的数 的概率大于 \(50 \%\)，经典的 \(Hash\) 碰撞估计

由此我们知道 组合随机采样 比 单次随机采样 满足条件的概率 高得多

这曾被用来快速有效的 估计鱼塘里鱼的条数（[6] 标记重捕法）

同样，这个原理也可以用来 分解质因数

\(Pollard\) 老师提出了这么一个 随机数生成方法

\[f (x) = (x ^ 2 + c) \bmod n \]

其中 \(c\) 是 随机常数，我们 随一个 \(x_1\)，然后我们 不停迭代，即 \(x_2 = f (x_1), x_3 = f (x_2)\)

然后每次取 \(k_i = f (x_i) - f (x_{i - 1})\)，求 \(\gcd (k_i, n)\)

若 该值 不为 \(1\)，我们就找到了一个 \(n\) 的 非平凡因子，返回

于是 递归求解 即可（即将 \(n\) 分为 该非平凡因子 和 \(n\) 除以该因子 两部分）

最终通过 \(Miller-Rabin\) 判定 当前因子 是否为素因子，若是则 终止并返回（无法再分解）

下面尝试证明其 时间复杂度，即 得到每个非平凡因子 的时间为 \(O (n ^ {\frac 1 4} \log n)\)

考虑这个 \(f (x)\) 的 性质， \(\forall x \equiv y \pmod p, f (x) \equiv f (y) \pmod p\)，其中 \(p \mid n\)

证明显然，\(x ^ 2 \equiv y ^ 2 \pmod p\) 即可

这等价于告诉我们，在 按照上述方法生成的序列 \(x_1, x_2, x_3, ..., x_n\) 中

若 \(x_i = x_j\) 则 \(x_{i + 1} = x_{j + 1}, ..., x_{i + k} = x_{j + k}\)

容易发现 当找到这样的一组 \(i, j\) 后，继续迭代的 \(f (x)\) 将 成环

显然 \(x_{i + (j - i)} = x_j = x_{j + (j - i)} = ... = x_{i + k (j - i)}\)，环长为 \(j - i\)

根据 生日悖论，若 \(x_k\) 在 \([0, n)\) 中 均匀随机，则只需要 \(O (\sqrt n)\) 次就可以找到相等的 \(x_i, x_j\)

故也就是说（在符合预期的情况下）\(i, j < O (\sqrt n)\)，则 序列中不同的数为 \(O(\sqrt n)\) 个种

而我们设 \(n\) 的 最小非平凡因子 为 \(m\)，显然有 \(m \le \sqrt n\)

若设 \(y_i = x_i \bmod m\)，同上述，容易说明 \(y_i\) 中有 \(O (\sqrt m) \le O (n ^ {\frac 1 4})\) 种 不同的数

注意到 \(f (x)\) 的性质不只对 \(n\) 成立，而是对任意 \(p \mid n\) 均成立

即 我们取相邻的两项 \(x_i, x_{i + 1}\) 做差，其结果为 \(m\) 整倍数 的概率约 \(\dfrac 1 {n ^ {\frac 1 4}}\)

换言之，按照算法流程，我们期望 \(O (n ^ {\frac 1 4})\) 次就可以找到一个 \(n\) 的 非平凡因子

其中一次 \(\gcd\) 需要 \(O (\log N)\) 的时间

根据上述证明，我们知道了 \(f (x)\) 会在 迭代一定次数（\(O (\sqrt n\)）后 产生环

于是 生成的整个序列 在坐标系上就形如 \(\rho\)，这也是 算法后半部分名字 的由来

显然此时的 \(k_i\) 产生重复，再去判断是 无意义的，故我们要 找到环后退出

若此时 仍未找到非平凡因子，则 换一个 \(c\) 与 \(x_1\) 重新开始即可

这里我们可以使用 \(Floyd\) 的方法，我们维护 两个 \(f (x)\) 生成的值 \(x, x'\)

初始时 \(x = x' = x_1\)，之后 \(x\) 每迭代一次，\(x'\) 就 迭代两次

即当 \(x = x_p\) 时 \(x' = x_{2p}\)，显然，当（初始之后）首次 \(x = x'\) 时，我们就找到了环

容易得出，此时有 $2p - p = $ 环长，也就是上述证明过程中的 \(j - i\)，期望 \(O (\sqrt n)\)

于是我们 迭代 \(O (\sqrt n)\) 次即可 正常退出，不会有大量浪费

可能会发现，当退出时 \(x\) 不一定遍历完整个环

但这是 无关紧要的，因为本身这只是一个 随机序列，遍历完整并不会有什么额外的优势

但一般而言 不要尝试跳过前半部分的遍历（即不要什么初始时 \(x = x_{10}\) 这样的事情）

因为显然，到环之前 出现有效答案的效率很高，不应浪费大量时间在判环上

于是我们可以写出 如下代码

namespace Pollard_Rho {
	namespace Miller_Rabin {}
	
	mt19937 r (time (0));
	
	inline long long Nxt (const long long x, const long long c, const long long n) {
		return ((__int128) x * x + c) % n;
	}
	
	inline long long solve (const long long n) {
		long long c = r () % n, x = r () % n, t = Nxt (x, c, n), pre = 0, tmp = 0, gcd_ = 0, cnt = 0, sqt = sqrt (n);
		
		while (x != t) {
			tmp = abs (x - pre);
			if ((gcd_ = __gcd (tmp, n)) > 1) return gcd_;
			pre = x, x = Nxt (x, c, n), t = Nxt (Nxt (t, c, n), c, n);
			if (++ cnt > sqt) break ;
		}
		
		return n;
	}
	
	inline void Solve (const long long n, vector <long long> &a) {
		if (Miller_Rabin::Check (n)) return a.push_back (n), void ();
		
		long long d = n;
		
		while (d == n) d = solve (n);
		
		Solve (d, a), Solve (n / d, a);
	}
}

其中 Miller_Rabin 部分就是上面部分，这里就省略了

但这东西 不太行，甚至过不去板子题 Luogu P4718 【模板】Pollard-Rho

考虑优化，看上去这个 \(\gcd\) 就 很令人火大，多了个 \(\log\)，和 \(\color {black} \textsf {H} \color {red} \textsf {anghang}\) 一样

显然，我们发现 \(\gcd\) 这个东西存在 这么一个性质

若 \(\gcd (a, n) > 1\)，则一定有 \(\gcd (ab, n) > 1\)

于是在计算的时候，我们可以把 每次的 \(pre\) 相乘并累积成一块

一定次数后再将这个 一块的 \(pre'\) 与 \(n\) 求一次 \(\gcd\)，若 \(> 1\)，直接返回即可

若存在一次使得 \(pre' = 0\)，为防止 丢失答案，我们 退出循环并暴力判断

玄学部分

1. 最佳 ”块长“ 约为 \(128\)（\(OI\) 范围）
2. 仍然注意前面 有效信息 密集，故实际块长按 \(1, 2, 4, ..., 128 , 128, 128 ...\) 这样取
3. 小质因数（\(2\)）之类的 较难被判断出来，性价比很低，可以直接特判
4. \(c\) 一般在 \([3, n)\) 范围内 比较容易出答案

于是我们就得到了 最终代码，也就是 能通过板子题 的版本

#include <bits/stdc++.h>

const int MAXN = 1000005;

using namespace std;

namespace Pollard_Rho {
	namespace Miller_Rabin {
	
		int P[15] = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37};
		int MAX_64 = 12;
		
		inline long long Qpow (__int128 a, long long b, const long long p) {
			__int128 Ret = 1;
			while (b) {
				if (b & 1) Ret = Ret * a % p;
				a = a * a % p, b >>= 1;
			}
			return Ret;
		}
		
		inline bool Check (const long long x) {
			if (x < 3 || !(x & 1)) return x == 2;
			long long d = x - 1, t = 0;
			__int128 v;
			while (!(d & 1)) d >>= 1, ++ t;
			for (int i = 0; i < MAX_64 && P[i] < x; ++ i) {
				v = Qpow (P[i], d, x);
				if (v == 1) continue ;
				for (int k = 0; k < t; ++ k) {
					if (v == x - 1) break ;
					v = v * v % x;
					if (k == t - 1) return 0;
				}
			}
			return 1;
		}
	}
	
	mt19937 r (time (0));
	
	inline long long Mul (const long long x, const long long y, const long long n) {
		long long d = x * (long double) y / n, ret = x * y - d * n;
		if (ret < 0) return ret + n;
		if (ret > n) return ret - n;
		return ret;
	}
	
	inline long long add (const long long a, const long long b, const long long n) {
		long long d = (a + (long double) b) / n + 0.5, ret = a + b - d * n;
		if (ret < 0) return ret + n;
		return ret;
	}
	
	inline long long Add (const __int128 a, const __int128 b, const long long n) {
		__int128 c = a + b;
		if (c >= n) return c - n;
		else return c;
	}
	
	inline long long Nxt (const long long x, const long long c, const long long n) {
		return Add (Mul (x, x, n), c, n);
		// return ((__int128) x * x + c) % n;
	}
	
	inline long long solve (const long long n) {
		if ((n & 1) == 0) return 2;
		
		long long c = r () % (n - 3) + 3, x = r () % n, t = Nxt (x, c, n);
		long long pre = 0, tmp = 0, gcd_ = 0;
		
		for (int lim = 1; x != t; lim = min (1 << 7, lim << 1)) {
			pre = 1, tmp = 0;
			for (int i = 1; i < lim; ++ i, pre = tmp) {
				tmp = Mul (pre, abs (Add (x, - t, n)), n);
			//	tmp = (__int128) pre * abs (t - x) % n;
				if (!tmp) break ;
				x = Nxt (x, c, n), t = Nxt (Nxt (t, c, n), c, n);
			}
			gcd_ = __gcd (pre, n);
			if (gcd_ > 1) return gcd_;
		}
		
		return n;
	}
	
	long long Ans = 0;
	
	inline void Solve (const long long n) {
		if (Miller_Rabin::Check (n)) return Ans = max (Ans, n), void ();
		
		long long d = n;
		
		while (d == n) d = solve (n);
		
		Solve (d), Solve (n / d);
	}
}

int T;
long long A;

int main () {
	
	cin >> T;
	
	for (int i = 1; i <= T; ++ i) {
		cin >> A, Pollard_Rho::Ans = 0;
		Pollard_Rho::Solve (A);
		if (Pollard_Rho::Ans == A) cout << "Prime" << '\n';
		else cout << Pollard_Rho::Ans << '\n';
	}
	
	return 0;
}

注意到我们每次乘 \(t - x\) 与 乘上 相邻两项 在 随机序列 的情况下

显然等价（出现因数的概率相等）

只是这样 好写，并没有什么 特殊性质

使用 快速乘 和 快速加 替换掉 __int128 后，效率 极大的提升，\(2.27 s \rightarrow 722 ms\)

Luogu P4358 [CQOI2016] 密钥破解

就是板子

给出 \(N = p \times q (p, q \in \mathbb P), e, c\)

而有 \(r = (p - 1) (q - 1), de \equiv 1 \pmod r, c ^ d \equiv n \pmod N\)

试求 \(d, n\)

这实质上就是 \(RSA\) 加密算法，这也是其需要 大质数 来 防止破译的原因（有 多项式算法）

容易发现 \(d\) 即是 \(e \bmod r\) 的 逆元，\(\operatorname {exgcd}\) 即可（\(r \notin \mathbb P\)，不可以用 费马小定理）

故重点在于求 \(r\)，显然知道 \(p, q\) 即可，于是 \(Pollard - rho\) 将 \(N\) 分解就行了

时间复杂度 \(O (N ^ {\frac 1 4})\)，只有一组数据，很轻松，甚至优化的 \(O (\sqrt N)\) 都能过

#include <bits/stdc++.h>

const int MAXN = 100005;

using namespace std;

namespace Pollard_Rho {
	namespace Miller_Rabin {
	
		int P[15] = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37};
		int MAX_64 = 12;
		
		inline long long Qpow (__int128 a, long long b, const long long p) {
			__int128 Ret = 1;
			while (b) {
				if (b & 1) Ret = Ret * a % p;
				a = a * a % p, b >>= 1;
			}
			return Ret;
		}
		
		inline bool Check (const long long x) {
			if (x < 3 || !(x & 1)) return x == 2;
			long long d = x - 1, t = 0;
			__int128 v;
			while (!(d & 1)) d >>= 1, ++ t;
			for (int i = 0; i < MAX_64 && P[i] < x; ++ i) {
				v = Qpow (P[i], d, x);
				if (v == 1) continue ;
				for (int k = 0; k < t; ++ k) {
					if (v == x - 1) break ;
					v = v * v % x;
					if (k == t - 1) return 0;
				}
			}
			return 1;
		}
	}
	
	mt19937 r (time (0));
	
	inline long long Mul (const long long x, const long long y, const long long n) {
		long long d = x * (long double) y / n, ret = x * y - d * n;
		if (ret < 0) return ret + n;
		if (ret > n) return ret - n;
		return ret;
	}
	
	inline long long add (const long long a, const long long b, const long long n) {
		long long d = (a + (long double) b) / n + 0.5, ret = a + b - d * n;
		if (ret < 0) return ret + n;
		return ret;
	}
	
	inline long long Add (const __int128 a, const __int128 b, const long long n) {
		__int128 c = a + b;
		if (c >= n) return c - n;
		else return c;
	}
	
	inline long long Nxt (const long long x, const long long c, const long long n) {
		return Add (Mul (x, x, n), c, n);
		// return ((__int128) x * x + c) % n;
	}
	
	inline long long solve (const long long n) {
		if ((n & 1) == 0) return 2;
		
		long long c = r () % (n - 3) + 3, x = r () % n, t = Nxt (x, c, n);
		long long pre = 0, tmp = 0, gcd_ = 0;
		
		for (int lim = 1; x != t; lim = min (1 << 7, lim << 1)) {
			pre = 1, tmp = 0;
			for (int i = 1; i < lim; ++ i, pre = tmp) {
				tmp = Mul (pre, abs (Add (x, - t, n)), n);
			//	tmp = (__int128) pre * abs (t - x) % n;
				if (!tmp) break ;
				x = Nxt (x, c, n), t = Nxt (Nxt (t, c, n), c, n);
			}
			gcd_ = __gcd (pre, n);
			if (gcd_ > 1) return gcd_;
		}
		
		return n;
	}
	
	inline void Solve (const long long n, vector <long long> &a) {
		if (Miller_Rabin::Check (n)) return a.push_back (n), void ();
		
		long long d = n;
		
		while (d == n) d = solve (n);
		
		Solve (d, a), Solve (n / d, a);
	}
}

using namespace Pollard_Rho::Miller_Rabin;

inline long long EXGCD (const long long a, const long long b, long long &x, long long &y) {
	if (b == 0) return x = 1, y = 0, a;
	long long d = EXGCD (b, a % b, y, x);
	y -= (a / b) * x; return d;
}

vector <long long> p;

long long N, e, c;

long long k, r, d, n;

int main () {
	
	cin >> e >> N >> c;
	
	Pollard_Rho::Solve (N, p);
	
	r = N - p[0] - p[1] + 1;
	
	EXGCD (e, r, d, k);
	
	d = (d % r + r) % r;
	
	n = Qpow (c, d, N);
	
	cout << d << ' ' << n << '\n';
	
	return 0;
}

\(Pollard-rho\) 的板子 过长了，后续考虑省略，则以此版本为准

Luogu P4714 「数学」约数个数和

需要用到一些 数论函数基础 里的内容

给定整数 \(N, K\)，试求 \(N\) 的（（所有约数的）\(\times K\)）的约数和

输出对 \(998244353\) 取模，\(N, K < 10 ^ {18}\)

考虑 \(K = 0\)，有 \(f_0 (x) = \sigma (x)\) 为 积性函数*

这里我们利用 积性函数 存在 \(f (x) f(y) = f (xy), x, y \in N ^ *\) 这个性质

此处 暂不给出 \(\sigma (x)\) （约数和）为积性函数的证明

然后有 \(K > 0\) 时，\(f_i (x) = \sum \limits _ {d \mid x} f_{i - 1} (d)\) ，这是 狄利克雷卷积 的形式

根据 狄利克雷卷积 的性质，可以知道 \(f_i (x)\) 仍为 积性函数

则我们可以将 \(n\) 质因数分解，将最后 结果的 \(f\) 相乘即可，形式化表达则是

\[f_K (n) = \prod (f_K (p_i ^ {q_i})) \]

其中 \(n = \prod p_i ^ {q_i}\) 是 \(n\) 的 唯一分解式

于是我们只需要考虑如何求 \(f_K (p ^ q)\) 即可，带回 \(f_i (x) = \sum \limits _ {d \mid x} f_{i - 1} (d)\)，可将其变形成

\[f_i (x) = \sum \limits _ {i = 1} ^ q f_{i - 1} (p ^ i) \]

可以发现，这等价于将 \(q\) 个位置分成 \(K + 1\) 份，每份可以为 \(0\)，插板法很好理解

故我们就是求 \({q + K + 1} \choose {K + 1}\)，容易变形成 \({q + K + 1} \choose {q}\)，显然 \(q \le 62\)，暴力做就行

然后其中 分解质因数 的部分需求 \(Pollard-rho\)，此处不放板子，参照上一道题

注意 \(N = 1\)！

#include <bits/stdc++.h>

using namespace std;

const int MOD = 998244353;

namespace Pollard_Rho {}

using namespace Pollard_Rho::Miller_Rabin;

struct Prime {
	long long v;
	int cnt;
} Pri[36];

int Cnt = 0;

inline void Add (const int p) {
	for (int i = 1; i <= Cnt; ++ i)
		if (Pri[i].v == p) return Pri[i].cnt ++, void ();
	Pri[++ Cnt].v = p, Pri[Cnt].cnt = 1;
}

vector <long long> Frac;

long long N, K;
long long Ans = 1;

inline long long F (const int q) {
	long long Ret = 1;
	for (int i = q; i >= 1; -- i) 
		Ret = (__int128) Ret * (i + K + 1) % MOD * Qpow (i, MOD - 2, MOD) % MOD;
	return Ret;
}

int main () {
	
	cin >> N >> K;
	
	if (N == 1) return cout << 1 << '\n', 0;
	
	Pollard_Rho::Solve (N, Frac);
	
	for (auto p : Frac) Add (p);
	
	for (int i = 1; i <= Cnt; ++ i)
		Ans = Ans * F (Pri[i].cnt) % MOD;
	
	cout << Ans << '\n';
	
	return 0;
}

总算结束力！

6. 引用资料

[0] Number Theory —— H_W_Y

[1] Stern–Brocot 树与 Farey 序列 —— OI - Wiki

[2] 「P8058 [BalkanOI2003] Farey 序列」—— _Fontainebleau_

[3] DIVCNT1 - Counting Divisors —— yhx-12243

[4] 卡迈克尔数 —— Wikipedia

[5] AKS素数测试 —— 百度百科

[6] 标记重捕法 —— 百度百科