基本概念

基本概念

全文 绝大多数 内容是对 [0] 中讲述的 粗略抄写 和 胡乱加工

1. 整除

整除记号 \(\mid\)

\mid

不整除记号 \(\nmid\)

\nmid

概念略

2. 整值函数

就是 小奥 里的 高斯记号，以及 取整符号

底 \(\lfloor ~ \rfloor\)，\(\lfloor x \rfloor = k_{\max}, k \le x,k \in \mathbb {Z}\)

$\lfloor x \rfloor = k_{\max}, k \le x,k \in \mathbb {Z}$

顶 \(\lceil ~ \rceil\)，\(\lceil x \rceil = k_{\min}, k \ge x, k \in \mathbb {Z}\)

$\lceil x \rceil = k_{\min}, k \ge x, k \in \mathbb {Z}$

即 下取整 和 上取整，显然存在 \(\left \lceil x \right \rceil - \left \lfloor x \right \rfloor \in \{0, 1\}\)

又有 \(x - \lfloor x \rfloor = \{x\}\)，\(\{x\}\) 就是 \(x\) 的 分数部分，同时称 \(\lfloor x \rfloor\) 为 \(x\) 的 整数部分

以下有一些 事实 / 定理，若 \(m \in \mathbb {Z}, n \in \mathbb {N ^ *}\)，则

\(\left \lfloor \dfrac {x + m} {n} \right \rfloor = \left \lfloor \dfrac {\left \lfloor x \right \rfloor + m} {n} \right \rfloor\) 且 \(\left \lceil \dfrac {x + m} {n} \right \rceil = \left \lceil \dfrac {\left \lceil x \right \rceil + m} {n} \right \rceil\)

考虑证明 左半部分，右半部分 同理

存在 \(0 \le x - \left \lfloor x \right \rfloor < 1\)，于是 \(0 \le \dfrac {x + m} {n} - \dfrac {\left \lfloor x \right \rfloor + m} {n} < \dfrac {1} {n}\)

而显然若 \(\dfrac {\left \lfloor x \right \rfloor + m} {n} \notin \mathbb {Z}\)，则 \(\left \lceil \dfrac {\left \lfloor x \right \rfloor + m} {n} \right \rceil - \dfrac {\left \lfloor x \right \rfloor + m} {n} \ge \dfrac {1} {n}\)

即显然 $\dfrac {x + m} {n} < \left \lceil \dfrac {\left \lfloor x \right \rfloor + m} {n} \right \rceil $，于是 上式成立

当 \(\dfrac {\left \lfloor x \right \rfloor + m} {n} \in \mathbb {Z}\) 时，显然 \(x - \left \lfloor x \right \rfloor < n\)，故 上式成立，即证毕

事实上，我们存在 下面这样的东西（H_W_Y 老师使用了这个结论 来推导上式）

若 \(f (x)\) 是一个 实数区间连续的单调递增函数，且满足当 \(f (x) \in \mathbb {Z}\) 时，\(x \in \mathbb {Z}\)

则只要 \(f(x), f(\left \lceil x \right \rceil), f (\left \lfloor x \right \rfloor)\) 有定义，就会有

\[\left \lfloor f (x) \right \rfloor = \left \lfloor f (\left \lfloor x \right \rfloor) \right \rfloor ~ 且 ~ \left \lceil f (x) \right \rceil = \left \lceil f (\left \lceil x \right \rceil) \right \rceil \]

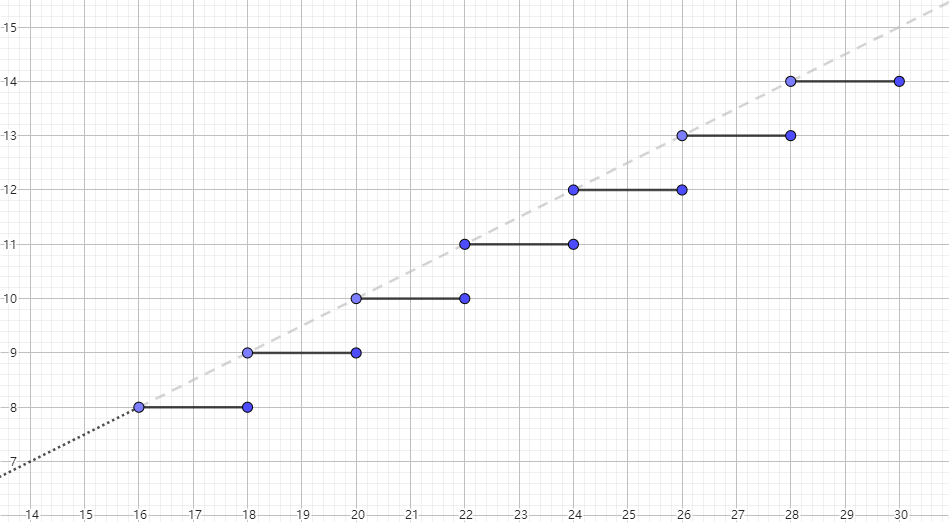
上图 纵轴 是 \(f (x)\)，横轴 是 \(x\)，虚线 是 原函数，实线 是 \(\left \lfloor f (x) \right \rfloor\) 的 值

容易发现上述结论成立，而 \(f (x) = \dfrac {x + m} {n}\) 也满足上面 \(f (x)\) 的 性质，于是结束

3. 带余除法

基本式 \(n = m \left \lfloor \dfrac {n} {m} \right \rfloor + n \bmod m\)，可以写成 \(n \bmod m = n - m \left \lfloor \dfrac {n} {m} \right \rfloor\)

后面一个式子 可以推广到实数域，虽然以下的 \(\bmod\) 运算 仍默认在整数域下

此时为了 完整性，特别定义 \(x \bmod 0 = x\)

余数有以下 基本性质

1. 可加性 \((a + b) \bmod p = (a \bmod p + b \bmod p) \bmod p\)

2. 可乘性 \((ab) \bmod p = (a \bmod p \times b \bmod p) \bmod p\)

3. 分配律 \(k (a \bmod b) = ka \bmod kb\)

4. 递进？\(a \bmod kb \bmod b = a \bmod b\)

以上均默认 \(a, b, c \in \mathbb {Z}\)，证明是简单的，此处略去

4. 同余关系

在 数论 中，我们常在 模意义下 对问题讨论

而同余，就可以理解成 模意义下 的 相等，十分重要

不排除在一些题解中将 同余 \(\equiv\) 和 相等 \(=\) 混用

我们使用 \(\equiv\) 来表示 同余

\[a \equiv b \pmod c \iff a \bmod c = b \bmod c \]

$a \equiv b \pmod c \iff a \bmod c = b \bmod c$

补充一些 推导符号

引用自 [1]

\(\leftarrow ~ \longleftarrow ~ \Leftarrow ~ \Longleftarrow ~ \leftrightarrow ~ \Leftrightarrow ~ \longleftrightarrow ~ \Longleftrightarrow ~ \rightarrow ~ \longrightarrow ~ \Rightarrow ~ \Longrightarrow\)

$\leftarrow ~  \longleftarrow ~ \Leftarrow ~ \Longleftarrow ~ \leftrightarrow ~ \Leftrightarrow ~ \longleftrightarrow ~ \Longleftrightarrow ~ \rightarrow ~ \longrightarrow ~ \Rightarrow ~ \Longrightarrow$

$\nleftarrow ~ \nLeftarrow ~ \nleftrightarrow ~ \nLeftrightarrow ~ \nrightarrow ~ \nRightarrow ~ $

$\nleftarrow ~  \nLeftarrow ~ \nleftrightarrow ~ \nLeftrightarrow ~ \nrightarrow ~ \nRightarrow ~ $

这玩意儿显然有下面这些性质

1. 一种变形 \(a \equiv b \pmod c \Longrightarrow c \mid |a - b|\)
2. 可加性 \(a \equiv b, c \equiv d \pmod m \Longrightarrow a + c \equiv b + d \pmod m\)
3. 可乘性 \(a \equiv b, c \equiv d \pmod m \Longrightarrow ac \equiv bd \pmod m\)
4. 可乘方 \(a \equiv b \pmod m \Longrightarrow a ^ n \equiv b ^ n \pmod m\)
5. 带限制的可除性 \(ac \equiv bc \pmod m \Longleftrightarrow a \equiv b \pmod {\dfrac {m} {\gcd (c, m)}}\)

容易发现，当 \(c \perp m\) 时，存在 \(ac \equiv bc \pmod m \Longleftrightarrow a \equiv b \pmod m\)

\(\perp\) 互质 符号

$\perp$

显然，只有 性质 \(5\) 不那么显然，因为 模意义下 并没有 直接的除法

但我们可以使用 乘上 乘法逆元 来代替 除法运算

就是 \(c ^ {-1}\) 的地位

令人火大的是，乘法逆元 仅在 与模数互质的数 上 有定义

故当 \(\gcd (c, m) \neq 1\) 时，我们 不得不 将模数缩小，使得其 与 \(c\) 互质

这样 乘上逆元 即可证明 上述性质

特别的，容易发现，当 \(m\) 为 质数 时，恒存在 \(ac \equiv bc \pmod m \Longleftrightarrow a \equiv b \pmod m\)

从 性质 \(5\) 进行 拓展，我们可以得出 下面的一些有趣的式子

\[a \equiv b \pmod {md} \Longrightarrow a \equiv b \pmod m \]

\(a = k_1 md + c, b = k_2 md + c\)，显然 \(m \mid k_1 md, k_2 md, c \equiv c \pmod m\)，得证

\[a \equiv b \pmod m, a \equiv b \pmod n \Longleftrightarrow a \equiv b \pmod {\operatorname {lcm} (n, m)} \]

注意 \(\operatorname {lcm}\) 不能 用 \(\gcd\) 的方法 简单的打出来

$\operatorname {lcm}$

注意到 \(\operatorname {lcm} (n, m) = \dfrac {nm} {\gcd (n, m)}\)，于是 向左推导 就是 性质 \(5\)

5. 引用资料

[0] Number Theory —— H_W_Y

[1] Latex各种箭头符号总结 —— Artoria____