3.可持久化树2024-05-03

4.树上差分等操作2024-05-03 5.树分治 - 点分治2024-05-04 6.树链剖分2024-05-06 7.树上启发式合并2024-05-29 8.支配对2024-05-29 9.K - D Tree2024-05-29 10.什么东西？DS！2024-12-23

可持久化

可持久化线段树

注意到 这里的内容 可能包括了 狭义的

可持久化线段树，可持久化权值线段树，”主席树“，可持久化 $T r i e$ ...

Luogu P3919 【模板】可持久化线段树 1（可持久化数组）

特定版本 单点修改，特定版本 单点查询，每次操作 生成新版本

单点查询则在 给定版本基础上 生成 一样的版本

就是 主席树（可持久化线段树）板子，这个东西不多讲

简单来说就是利用线段树 单点修改只影响 $\log N$ 个区间的性质

在原树上每次修改 新增 $\log N$ 个修改后的节点，记录新节点的根即可

注意到此时的 “主席树” 实质上 不是一棵树，而是一个 $D A G$

~~好图，偷了~~

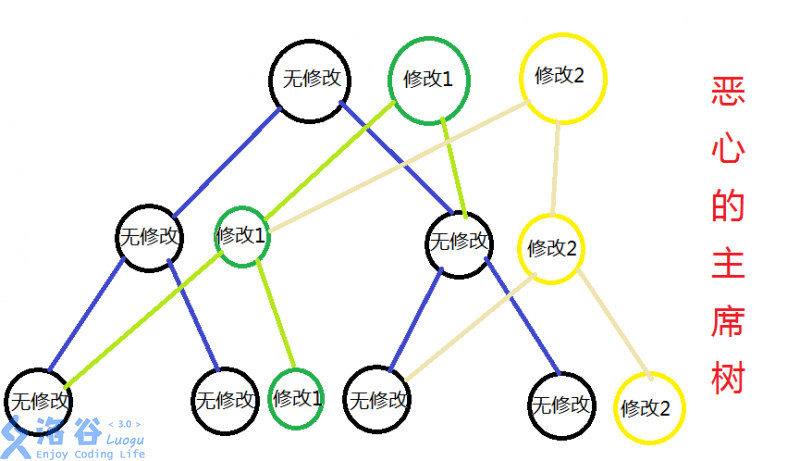
然后这个题就很简单了，看代码就行

#include <bits/stdc++.h>

const int MAXN = 1000005;
const int LOGN = 24;

using namespace std;

int Num[MAXN];

namespace PSDTree {
	struct Node {
		int L, R, v, lc, rc;
	} T[MAXN * LOGN];
	
	int RT[MAXN], tot, Cnt;
	
	#define LC T[x].lc
	#define RC T[x].rc
	#define M ((T[x].L + T[x].R) >> 1)
	
	inline int NewNode (const int x) {
		return T[++ tot] = T[x], tot;
	}
	
	inline int Build (const int L, const int R, int x = 0) {
		x = ++ tot, T[x].L = L, T[x].R = R;
		if (L == R) return T[x].v = Num[L], x;
		LC = Build (L, M), RC = Build (M + 1, R);
		return x;
	}
	
	inline int Modify (const int p, const int v, int x = 0) {
		x = NewNode (x);
		if (T[x].L == T[x].R) return T[x].v = v, x;
		if (p <= M) LC = Modify (p, v, LC);
		else RC = Modify (p, v, RC);
		return x;
	}
	
	inline int Query (const int p, const int x = 0) {
		if (T[x].L == T[x].R) return T[x].v;
		if (p <= M) return Query (p, LC);
		else return Query (p, RC);
	}
	
	#undef M
}

using namespace PSDTree;

int N, M;
int Ver, Opt, P, x;

int main () {
	
	ios::sync_with_stdio(0);
	cin.tie(0), cout.tie(0);
	
	cin >> N >> M;
	
	for (int i = 1; i <= N; ++ i) cin >> Num[i];
	
	RT[Cnt ++] = Build (1, N);
	
	for (int i = 1; i <= M; ++ i, ++ Cnt) {
		cin >> Ver >> Opt >> P;
		if (Opt == 1) cin >> x, RT[Cnt] = Modify (P, x, RT[Ver]);
		if (Opt == 2) RT[Cnt] = RT[Ver], cout << Query (P, RT[Ver]) << '\n';
	}
	
	return 0;
}

Luogu P3834 【模板】可持久化线段树 2

给定有 $N$ 个正整数构成的序列 $a$ ，查询区间 $[L, R]$ 里面的第 $k$ 小值

就是 可持久化权值线段树 的板子，如果是 动态区间 $k$ 小 就得 树套树 了

我们 每插入一个数就新建一个版本，一个区间 其实就是 两个版本的差值

然后查询的时候就是 两树之间做差分，然后有点像 线段树分治 的感觉

如果 左子树差值大于 $k$ ，则向左子树走，否则向右子树走， $k$ 减去 左子树差值

然后注意 权值离散化 就行了

#include <bits/stdc++.h>

const int MAXN = 200005;
const int LOGN = 24;

using namespace std;

int Num[MAXN], Uni[MAXN];
unordered_map <int, int> Mp;

namespace PSDTree {
	struct Node {
		int L, R, v, lc, rc;
	} T[MAXN * LOGN];
	
	int RT[MAXN], tot = 0, Cnt = 0;
	
	#define LC T[x].lc
	#define RC T[x].rc
	#define M ((T[x].L + T[x].R) >> 1)
	
	inline int NewNode (const int x) {
		return T[++ tot] = T[x], tot;
	}
	
	inline int Build (const int L, const int R, int x = 0) {
		x = ++ tot, T[x].L = L, T[x].R = R;
		if (L == R) return x;
		LC = Build (L, M), RC = Build (M + 1, R);
		return x;
	}
	
	inline int Ins (const int p, int x = 0) {
		x = NewNode (x), T[x].v ++ ;
		if (T[x].L == T[x].R) return x;
		if (p <= M) LC = Ins (p, LC);
		else RC = Ins (p, RC);
		return x;
	}
	
	inline int Query (const int L, const int R, const int k) {
		if (T[L].L == T[L].R) return T[L].L;
		int New = T[T[R].lc].v - T[T[L].lc].v;
		if (k <= New) return Query (T[L].lc, T[R].lc, k);
		else return Query (T[L].rc, T[R].rc, k - New);
	}
	
	#undef M
}

using namespace PSDTree;

int N, M, L, R, k;

int main () {
	
	ios::sync_with_stdio(0);
	cin.tie(0), cout.tie(0);
	
	cin >> N >> M;
	
	for (int i = 1; i <= N; ++ i) cin >> Num[i];
	
	memcpy (Uni, Num, sizeof Num);
	sort (Uni + 1, Uni + N + 1);
	
	for (int i = 1; i <= N; ++ i) Mp[Uni[i]] = i;
	
	RT[Cnt ++] = Build (1, N);
	
	for (int i = 1; i <= N; ++ i) RT[i] = Ins (Mp[Num[i]], RT[i - 1]);
	
	for (int i = 1; i <= M; ++ i) 
		cin >> L >> R >> k, cout << Uni[Query (RT[L - 1], RT[R], k)] << '\n';
	
	return 0;
}

Luogu P5795 [THUSC2015] 异或运算

注意到 $N, M$ 不同阶， $M$ 有 $3 \times 10^{5}$ ，所以 $O (N M \log M)$ 之类的暴力不可取

考虑 异或的性质，注意到可以贪心，高位尽量选 $1$ 一定大

可以对 $M$ 对应的的 $Y$ 序列建立 可持久化 $T r i e$

考虑每次给定 $X$ 序列区间，于是我们 暴力多树二分

具体一点，我们二进制下 一位一位的贪心 找到第 $k$ 大值

$A_{i, j}$ 在二进制下第 $t$ 位为 $1$ 的数个数实质上是

$X_{i} (i \in [u, d])$ 中第 $t$ 位为 $0$ 的数个数 $\times$ $Y_{i} (i \in [l, r])$ 中第 $t$ 位为 $1$ 的数个数

$+$ $X_{i} (i \in [u, d])$ 中第 $t$ 位为 $1$ 的数个数 $\times$ $Y_{i} (i \in [l, r])$ 中第 $t$ 位为 $0$ 的数个数

将 $X_{i} (i \in [u, d])$ 代入进行 多树二分 即可

注意需要记录下每个 $X_{i}$ 在 $T r i e$ 上 上一步走的是左 / 右子树

具体看代码吧，讲的有些抽象

#include <bits/stdc++.h>

const int MAXN = 1005;
const int MAXM = 300005;
const int LOGN = 22;
const int LOGV = 32;

using namespace std;

int N, M, Q;
int A[MAXN], B[MAXM];

namespace PSDTree {
	struct Node {
		int v, ch[2];
	} T[MAXM * LOGV];
	
	int RT[MAXM], tot = 0, Cnt = 0;
	
	inline int NewNode (const int x) {
		return T[++ tot] = T[x], tot;
	}
	
	inline int Ins (const int p, int x = 1) {
		int t, ret; ret = x = NewNode (x), ++ T[x].v;
		for (int i = 30; ~ i; -- i) {
			t = (p >> i) & 1;
			T[x].ch[t] = NewNode (T[x].ch[t]);
			x = T[x].ch[t], ++ T[x].v;
		}
		return ret;
	}
	
	int rd[MAXN], ld[MAXN];
	bool v[MAXN][LOGV];
	
	inline int Query (const int l1, const int r1, const int l2, const int r2, int K) {
		int Ret = 0, cnt = 0, t = 0;
		for (int i = l1; i <= r1; ++ i) rd[i] = RT[r2];
		for (int i = l1; i <= r1; ++ i) ld[i] = RT[l2];
		
		for (int k = 30; ~ k; -- k, cnt = 0) {
			for (int i = l1; i <= r1; ++ i) t = v[i][k], cnt += T[T[rd[i]].ch[t ^ 1]].v - T[T[ld[i]].ch[t ^ 1]].v;
			
			if (K <= cnt) {
				Ret += (1 << k);
				for (int i = l1; i <= r1; ++ i) t = v[i][k], rd[i] = T[rd[i]].ch[t ^ 1], ld[i] = T[ld[i]].ch[t ^ 1];
			} else {
				K -= cnt;
				for (int i = l1; i <= r1; ++ i) t = v[i][k], rd[i] = T[rd[i]].ch[t], ld[i] = T[ld[i]].ch[t];
			}
		}
		return Ret;
	}
}

using namespace PSDTree;

int U, D, L, R, K;

int main () {
	
	ios::sync_with_stdio(0);
	cin.tie(0), cout.tie(0);

	cin >> N >> M;
	
	for (int i = 1; i <= N; ++ i) cin >> A[i];
	
	for (int i = 1; i <= M; ++ i) cin >> B[i];
	
	for (int i = 1; i <= M; ++ i) RT[i] = Ins (B[i], RT[i - 1]);
	
	for (int i = 30; ~ i; -- i) 
		for (int j = 1; j <= N; ++ j) 
			v[j][i] = (A[j] >> i) & 1;
	
	cin >> Q;
	
	for (int i = 1; i <= Q; ++ i) {
		cin >> U >> D >> L >> R >> K;
		cout << Query (U, D, L - 1, R, K) << '\n';
	}
	
	return 0;
}

Luogu P2839 [国家集训队] middle

好题，牛牛的一个套路 —— $H$ $anghang$

就是题面比较如如

可以 理解成 对于序列 $A$ ， $a_{1} . . . a_{N}$ ，中位数 是 $a_{N / 2}$ ，其中 除法上取整

直接维护是 困难的，但是注意到我们要维护一个 中位数的最大值

可以考虑 极值转存在 —— 二分答案

对于一个区间，如果我们把 大于等于 $k$ 的所有数 记为 $1$ ，反之为 $- 1$

容易发现，当这个 区间和 大于等于 $0$ 时，这个区间中位数 将 大于等于 $k$

于是我们只需要考虑 如何维护这个区间和 就行了

注意到每个询问给出了 左右端点所在区间，显然想让 中位数大，那么 区间和应当大

于是我们用 线段树维护 区间 最大前缀 $S u f$ ， 最大后缀 $P r e$ ，区间和 $S u m$

不难发现对于左端点在 $[L_{1}, R_{1}]$ ，右端点在 $[L 2, R 2]$ 范围内的 所有区间 $[l_{i}, r_{i}]$

其 最大区间和 应当是 $P r e_{L 1, R 1} + S u m_{R 1 + 1, L 2 - 1} + S u f_{L 2, R 2}$

但是我们注意到，这里的 $- 1, 1$ 序列是 对于某个数 $k$ 而言的

当 最大区间和大于等于 $0$ 时，这个询问的 最大中位数大于等于 $k$

我们需要 二分答案，故对于 每个可能的 $k$ ，我们 都需要 预处理出这个 $- 1, 1$ 序列与线段树

而 $k$ 的可能取值即种数序列长度 $N$ ，显然我们不可能处理出 $N$ 个这样的 $- 1, 1$ 序列

但是我们观察到，当 $k$ 不断变大时，更多的数从 $1$ 变成 $- 1$ ，且不会变回来

也就是说这 $N$ 个序列中实质上 只有 $N$ 次单向的变化，可以想到用 可持久化数据结构维护

于是此处我们 建立一棵主席树 来维护上述 区间信息

同时 所有位置初始值为 $1$ ，从小到大 遍历权值

将 当前遍历到的权值对应位置 改为 $- 1$ ，并 建立新版本

于是我们得到了有 $N$ 个版本的主席树，其中 第 $i$ 个版本 就对应了 $k = i + 1$ 时的 线段树

这里 $k = i + 1$ 是指的 $k$ 等于排序后 第 $i + 1$ 小的数

注意到我们建立的不是 权值线段树，故此处 不能离散化去重，每个值都有其贡献

代码还是比较简单的

#include <bits/stdc++.h>

const int MAXN = 25005;
const int LOGN = 16;

using namespace std;

int N, M, LA;
int Num[MAXN], Uni[MAXN];
int Q[4];

namespace PSDTree {
	struct Node {
		int L, R, lc, rc;
		int Sum = 0, Pre = 0, Suf = 0;
	} T[MAXN * LOGN << 1];
	
	int RT[MAXN], tot = 0, Cnt = 0;
	
	#define LC T[x].lc
	#define RC T[x].rc
	#define M ((T[x].L + T[x].R) >> 1)
	
	inline int NewNode (const int x) {
		return T[++ tot] = T[x], tot;
	}
	
	inline int ModNode (const int x, const int v) {
		return T[x].Sum = T[x].Pre = T[x].Suf = v;
	}
	
	inline void Update (const int x) {
		T[x].Sum = T[LC].Sum + T[RC].Sum;
		T[x].Pre = max (T[RC].Sum + T[LC].Pre, T[RC].Pre);
		T[x].Suf = max (T[LC].Sum + T[RC].Suf, T[LC].Suf);
	}
	
	inline int Build (const int L, const int R, int x = 0) {
		x = ++ tot, T[x].L = L, T[x].R = R;
		if (L == R) return ModNode(x, 1), x;
		LC = Build (L, M), RC = Build (M + 1, R), Update (x);
		return x;
	}
	
	inline int Ins (const int p, const int v, int x = 0) {
		x = NewNode (x);
		if (T[x].L == T[x].R) return ModNode (x, v), x;
		if (p <= M) LC = Ins (p, v, LC), Update (x);
		else RC = Ins (p, v, RC), Update (x);
		return x;
	}
	
	inline int Sum (const int L, const int R, const int x = 0) {
		if (T[x].L > R || T[x].R < L) return 0;
		if (L <= T[x].L && T[x].R <= R) return T[x].Sum;
		return Sum (L, R, LC) + Sum (L, R, RC);
	}
	
	inline int Pre (const int L, const int R, const int x = 0) {
		if (T[x].L > R || T[x].R < L) return -1e9;
		if (L <= T[x].L && T[x].R <= R) return T[x].Pre;
		return max (Sum (L, R, RC) + Pre (L, R, LC), Pre (L, R, RC));
	}
	
	inline int Suf (const int L, const int R, const int x = 0) {
		if (T[x].L > R || T[x].R < L) return -1e9;
		if (L <= T[x].L && T[x].R <= R) return T[x].Suf;
		return max (Sum (L, R, LC) + Suf (L, R, RC), Suf (L, R, LC));
	}
	
	#undef M
}

using namespace PSDTree;

inline bool Check (const int x, const int L1, const int R1, const int L2, const int R2) {
	int Ret = Pre (L1, R1, RT[x - 1]) + Sum (R1 + 1, L2 - 1, RT[x - 1]) + Suf (L2, R2, RT[x - 1]); // Node >= x -> 1, Node < x -> 0
	return Ret >= 0;
}

inline void Solve (const int L1, const int R1, const int L2, const int R2) {
	int L = 0, R = N, Mid = (L + R) >> 1, Ans = Mid;
	while (L <= R) {
		Mid = (L + R) >> 1;
		if (Check (Mid, L1, R1, L2, R2)) L = Mid + 1, Ans = Mid;
		else R = Mid - 1;
	}
	cout << (LA = Uni[Ans]) << '\n';
}

struct Value {
	int v, id;
	
	inline bool operator < (const Value &a) const {
		return v < a.v;
	}
} Secret[MAXN];

int main () {
	
	ios::sync_with_stdio(0);
	cin.tie(0), cout.tie(0);
	
	cin >> N;
	
	for (int i = 1; i <= N; ++ i) cin >> Num[i], Secret[i] = {Num[i], i};
	
	memcpy (Uni, Num, sizeof Num);
	
	sort (Uni + 1, Uni + N + 1), sort (Secret + 1, Secret + N + 1);
	
	RT[0] = Build (1, N);
	
	for (int i = 1; i <= N; ++ i) RT[i] = Ins (Secret[i].id, -1, RT[i - 1]);
	
	cin >> M;
	
	for (int i = 1; i <= M; ++ i) {
		cin >> Q[0] >> Q[1] >> Q[2] >> Q[3];
		Q[0] = (Q[0] + LA) % N + 1;
		Q[1] = (Q[1] + LA) % N + 1;
		Q[2] = (Q[2] + LA) % N + 1;
		Q[3] = (Q[3] + LA) % N + 1;
		sort (Q, Q + 4), Solve (Q[0], Q[1], Q[2], Q[3]);
	}
	
	return 0;
}

CF464E The Classic Problem

典题

注意到这道题 $N, M, K$ 同阶，故下文部分 时间复杂度 的分析可能 不会区分 $N, M, K$

最短路问题，边权改为 $2^{k}$ ， $k \leq 10^{5}$ ，求 最短路距离与路径（ $N, M \leq 10^{5}$ ）

显然问题的关键在这个 $2^{k}$ 的边权，而真正 最短路部分 由于 没有什么其他性质

所以仍然考虑朴素的 $D i j k s t r a$ 算法

于是当前需要解决的就是 距离的比较 以及更新（加法，修改）问题

我们将维护的距离用一个 $01$ 序列来表示，单边边权 $2^{k}$ 就是一个 $1$ 后面 若干个 $0$ 的序列

这里默认序列长为 $max k$ ，实际上单边边权至多 $2^{10^{5}}$ ，而最多 $10^{5}$ 条边

故序列长 至少为 $10^{5} + 17$

于是 距离的比较 本质上就是两个 $01$ 序列，比较 字典序大小

我们可以使用二分 + $H a s h$ 来实现，具体来说，我们二分出 两序列上第一个值不同的位置

比较该位的值即可，单次比较的时间复杂度是 $O (\log N)$ 的

只剩下 距离更新 的问题了，容易发现，距离 加上一个边权 的实质是

将距离对应的 $01$ 序列一段连续的 $1$ 改成 $0$ ，然后将原本这段 $1$ 前面的第一个 $0$ 改成 $1$

$e g . 0110 1000 1111 0010 + 0000 0000 0001 0000 = 0110 1001 0000 0010$

于是我们需要维护 单点 $0 \to 1$ 和 区间 $1 \to 0$ 的操作，容易想到 线段树维护

对每一个 $01$ 序列 建立线段树

对于结点 $x \to [L, R] ，$ 我们钦定其 右子结点 将维护 $[M + 1, R]$ ，对应 $2^{M + 1} \sim 2^{R}$

实际上在 $01$ 序列中可能是 左边的值，注意区分

我们维护 区间长 $S i z$ ，区间后缀 $1$ 最大长度 $P r e$ ，区间 $H a s h$ 值 $H s h$ 三个信息

这里的后缀指的是 将距离二进制表达下的 $01$ 序列后缀

在我们维护的 $01$ 序列（左起 $0$ 到右止于 $10^{5} + 17$ ）中 可能是一段前缀

就和上面 右子结点 的理解一样，实际上就是因为 写的时候是从最高位开始写的

注意倒过来就行

其中 $S i z$ 和 $H s h$ 是简单的，不知道咋搞就看代码，容易理解

$P r e$ 的更新需要注意一些细节，我们判断一下 左区间 是否都是 $1$

如果是，那么 $P r e$ 就是 左区间的长度 $+$ 右区间的 $P r e$

反之直接取 左区间的 $P r e$ 即可

总结一下 加上一个边权 的流程

找到 从边权的 $1$ 所在位 向前的一段连续 $1$ ，通过维护的 区间最大后缀 可 $O (\log N)$ 找出
将这段连续 $1$ 改为 $0$ ，这里也是 $O (\log N)$ 的复杂度，方法比较妙，下面讲
将前面的第一个 $0$ 改为 $1$ ，单点修改，时间也是 $O (\log N)$

但是这里我们又发现一个 经典的问题

我们显然不能对 每个点的距离 都去维护一个 完整的 $01$ 序列

但是这里 修改次数 又很有限，只有 $D i j k s t r a$ 的 $O (M \log N)$ 次

于是 可持久化线段树 维护即可，注意到每个点的距离 对应一个版本的根

$D i s_{v} = D i s_{u} + w$ 的时候我们 以 $u$ 对应版本 为基础修改，将 $v$ 对应版本 改为这个新版本

原来 $v$ 对应的版本就被 弃用了

这里是可以做 内存回收 的，但是影响 时间常数，而且不做也能过...

而 区间修改 的操作呢？注意到我们 建立一个对应全 $0$ 序列的版本

每次修改，当前结点的区间被需要修改的区间包含时

我们直接将 这个结点 换成 全 $0$ 序列版本的对应结点 即可，实现也可以看代码

剩下的细节 不是很多，大胆实现就行

时间复杂度 $O (M \log N \log k = O (N \log^{2} N)$

空间复杂度 $O (M \log N \log K) = O (N \log^{2} N)$ 卡不满，内存回收后可以做到 $O (N \log k)$

$\log^{2} N$ 空间的话开满差不多 $400 M B$ ，没有问题

#include <bits/stdc++.h>

const int MAXN = 100050;
const int MOD  = 1000000007;
const int LOGN = 80;
const int D = 100020;

using namespace std;

int N, M, U, V;

struct Edge {
	int to, nxt, w;
} E[MAXN << 1];

int H[MAXN], tot1;

inline void Add_Edge (const int u, const int v, const int w) {
	E[++ tot1] = {v, H[u], w}, H[u] = tot1;
	E[++ tot1] = {u, H[v], w}, H[v] = tot1;
}

unsigned long long P[MAXN];

namespace PSDTree {
	struct Node {
		int L, R, lc, rc;
		int Siz, Pre;
		unsigned long long Hsh = 0;
	} T[MAXN * LOGN];
	
	int RT[MAXN], tot = 0, Cnt = 0;
	
	#define LC T[x].lc
	#define RC T[x].rc
	#define M ((T[x].L + T[x].R) >> 1)
	
	inline int NewNode (const int x) {
		return T[++ tot] = T[x], tot;
	}
	
	inline void Update (const int x) {
		T[x].Siz = T[LC].Siz + T[RC].Siz;
		T[x].Pre = (T[LC].Pre == T[LC].Siz) * T[RC].Pre + T[LC].Pre;
		T[x].Hsh = (T[RC].Hsh * P[T[LC].Siz] % MOD + T[LC].Hsh) % MOD;
	}
	
	inline int Build (const int L, const int R, int x = 0) {
		x = ++ tot, T[x].L = L, T[x].R = R;
		if (L == R) return T[x].Siz = 1, x;
		LC = Build (L, M), RC = Build (M + 1, R), Update (x);
		return x;
	}
	
	inline int Pre (const int L, const int R, const int x = 0) {
		if (R < T[x].L || T[x].R < L) return 0;
		if (L <= T[x].L && T[x].R <= R) return T[x].Pre;
		int LCP = Pre (L, R, LC), LCS = max (min (T[LC].R, R) - max (T[LC].L, L) + 1, 0);
		return LCP == LCS ? LCP + Pre (L, R, RC) : LCP;
	}
	
	inline int Modify_1_0 (const int L, const int R, const int Clr = RT[0], int x = 0) {
		if (L <= T[x].L && T[x].R <= R) return x = Clr;
		x = NewNode (x);
		if (L <= M) LC = Modify_1_0 (L, R, T[Clr].lc, LC);
		if (R >  M) RC = Modify_1_0 (L, R, T[Clr].rc, RC);
		return Update (x), x;
	}
	
	inline int Modify_0_1 (const int p, int x = 0) {
		x = NewNode (x);
		if (T[x].L == T[x].R) return T[x].Pre = T[x].Hsh = 1, x;
		if (p <= M) LC = Modify_0_1 (p, LC);
		else RC = Modify_0_1 (p, RC);
		return Update (x), x;
	}
	
	inline void Modify (int &Ans, const int Gen, const int Add) {
		int p = Pre (Add, D, Gen);
		if (p) Ans = Modify_1_0 (Add, Add + p - 1, RT[0], Gen); else Ans = Gen;
		Ans = Modify_0_1 (Add + p, Ans);
	}
	
	inline bool Cmp (const int x, const int y) { // return x > y ?
		if (T[x].L == T[x].R) return T[x].Hsh > T[y].Hsh;
		if (T[T[x].rc].Hsh == T[T[y].rc].Hsh) return Cmp (T[x].lc, T[y].lc);
		return Cmp (T[x].rc, T[y].rc);
	} 
	
	#undef M
}

struct Que {
	int id, rt;
	inline bool operator < (const Que &a) const {
		return PSDTree::Cmp (rt, a.rt);
	}
};

priority_queue <Que> Q;
int Pat[MAXN];
bool Vis[MAXN];

inline void Dijkstra () {
	using namespace PSDTree;
	RT[U] = RT[0], Q.push ({U, RT[U]});
	while (!Q.empty ()) {
		int u = Q.top ().id, v; Q.pop ();
		if (Vis[u]) continue ;
		Vis[u] = 1;
		if (u == V) break ;
		for (int i = H[u]; i; i = E[i].nxt) {
			Modify (RT[N + 1], RT[u], E[i].w), v = E[i].to;
			if (!RT[v] || Cmp (RT[v], RT[N + 1])) {
				RT[v] = RT[N + 1], Pat[v] = u; 
				if (!Vis[v]) Q.push ({v, RT[v]});
			}
		}
	}
}

int u, v, w;

stack <int> S;

int main () {
	
	ios::sync_with_stdio(0);
	cin.tie(0), cout.tie(0);
	
	cin >> N >> M;
	
	for (int i = 1; i <= M; ++ i)
		cin >> u >> v >> w, Add_Edge (u, v, w);
	
	P[0] = 1;
	for (int i = 1; i <= D; ++ i) P[i] = P[i - 1] * 2 % MOD;
	
	cin >> U >> V;
	
	PSDTree::RT[0] = PSDTree::Build (0, D);
	
	Dijkstra ();
	
	if (!Vis[V]) return cout << -1 << endl, 0;
	
	else cout << PSDTree::T[PSDTree::RT[V]].Hsh << endl;
	
	for (int i = V; i != U; i = Pat[i]) S.push (i); 
	
	S.push (U); cout << S.size () << endl;
	
	while (!S.empty ()) cout << S.top () << ' ', S.pop ();
	
	return 0;
}

Luogu P3302 [SDOI2013] 森林

感觉大体思路是简单的

考虑只有 $O p t .1$ 时，对 树建主席树

也就是 $D F S$ 一遍树，每个点 基于它父亲的版本 插入它自己的权值

然后 树上差分询问 即可，这里注意 版本不是 $D F S$ 序

而是 子节点继承父节点 信息

于是 T[RT[u]] - T[RT[F[LCA]]] 相当于 $L C A \to u$ 的 路径信息

另一边就是 $L C A$ 的儿子到 $v$ 的 路径信息（ $L C A$ 不能算两遍）

询问是简单的，考虑连边，即 $O p t .2$

不想写 $L C T$ ，所以考虑 启发式合并 的思路，小树往大树合并

然后直接 暴力重构， $D F S$ 后 重建主席树 即可

总复杂度 $O (N \log^{2} N)$ ，虽然常数较大，但是还是很轻松

注意到 $i >= 0$ 和 $i$ 并不等价，在求 $L C A$ 的最后那个循环 终止条件写成 $i$

怒调 $3 H r s$ ，本来多好写一道题...

#include <bits/stdc++.h>

const int MAXN = 100005;
const int LOGN = 90;

using namespace std;

int Val[MAXN], Uni[MAXN], Tmp;

struct Edge {
	int to, nxt;
} E[MAXN << 1];

int H[MAXN], tot;

inline void Add_Edge (const int u, const int v) {
	E[++ tot] = {v, H[u]}, H[u] = tot;
	E[++ tot] = {u, H[v]}, H[v] = tot;
}

namespace PSDTree {
	struct Node {
		int lc, rc;
		int s;
	} T[MAXN * LOGN];
	
	#define LC T[x].lc
	#define RC T[x].rc
	#define M ((L + R) >> 1)
	
	int RT[MAXN], Cnt = 0;
	int Tot = 0;
	
	inline int Cpy (const int x) {
		return T[++ Tot] = T[x], Tot;
	}
		
	inline int Ins (int x, const int v, const int L = 1, const int R = Tmp) {
		x = Cpy (x), ++ T[x].s;
		if (L == R) return x;
		if (v <= M) LC = Ins (LC, v, L, M);
		else RC = Ins (RC, v, M + 1, R);
		return x;
	}
	
	inline int Que (const int k, const int u, const int v, const int lca, const int flca, const int L = 1, const int R = Tmp) {
		if (L == R) return Uni[L];
		int Siz = T[T[u].lc].s + T[T[v].lc].s - T[T[lca].lc].s - T[T[flca].lc].s;
		if (k <= Siz) return Que (k, T[u].lc, T[v].lc, T[lca].lc, T[flca].lc, L, M);
		else return Que (k - Siz, T[u].rc, T[v].rc, T[lca].rc, T[flca].rc, M + 1, R);
	}

	#undef M
}

using namespace PSDTree;

int F[MAXN][LOGN], FF[MAXN], S[MAXN], D[MAXN];
int LOG[MAXN];

inline void DFS (const int x, const int f, const int rt) {
	RT[x] = Ins (RT[f], Val[x]);
	F[x][0] = f, FF[x] = rt, S[rt] ++ , D[x] = D[f] + 1;
	for (int i = 1; i < 18; ++ i)
		F[x][i] = F[F[x][i - 1]][i - 1];
	for (int i = H[x]; i; i = E[i].nxt)
		if (E[i].to != f) DFS (E[i].to, x, rt);
}

inline int LCA (int u, int v) {
	if (D[u] < D[v]) swap (u, v);
	while (D[u] != D[v]) u = F[u][LOG[D[u] - D[v]]];
	if (u == v) return u;
	
	
	for (int i = LOG[D[u]]; i >= 0; -- i)
		if (F[u][i] != F[v][i])
			u = F[u][i], v = F[v][i];
			
	return F[u][0];
}

int P, N, M, Q;
int u, v, k;
char Opt;
int Ans;

int main () {
	
	ios::sync_with_stdio(0);
	cin.tie(0), cout.tie(0);
	
	cin >> P >> N >> M >> Q;
	
	for (int i = 1; i <= N; ++ i) cin >> Val[i], Uni[i] = Val[i];
	
	for (int i = 2; i <= N; ++ i) LOG[i] = LOG[i >> 1] + 1;
	
	sort (Uni + 1, Uni + N + 1);
	
	Tmp = unique (Uni + 1, Uni + N + 1) - (Uni + 1);
	
	for (int i = 1; i <= N; ++ i) Val[i] = lower_bound (Uni + 1, Uni + N + 1, Val[i]) - Uni;
	
	for (int i = 1; i <= M; ++ i)
		cin >> u >> v, Add_Edge (u, v);
	
	for (int i = 1; i <= N; ++ i)
		if (!FF[i]) DFS (i, 0, i);
	
	for (int i = 1; i <= Q; ++ i) {
		cin >> Opt >> u >> v;
		u ^= Ans, v ^= Ans;
		if (Opt == 'Q') {
			cin >> k, k ^= Ans;
			P = LCA (u, v);
			cout << (Ans = Que (k, RT[u], RT[v], RT[P], RT[F[P][0]])) << '\n';
		} else {
			Add_Edge (u, v);
			if (S[FF[v]] < S[FF[u]]) DFS (v, u, FF[u]);
			else DFS (u, v, FF[v]);
		}
	}
	
	return 0;
}

Luogu P7561 [JOISC 2021 Day2] 道路の建設案 (Road Construction)

小清新 $D S$ ，甚至都不算 $D S$ ？

$N$ 个位置，求 曼哈顿距离 最小的 $K$ 个

$K D - T r e e$ 是 什么东西，蛤？

注意一个套路即 曼哈顿距离 转 切比雪夫距离

目的就是把 曼哈顿距离 这个 和两维差都相关 的值

转化成 切比雪夫距离 这个 和两维差最大值相关 的值

对于 原坐标系 的点 $(x_{i}, y_{i})$ ，转化成 $(x_{i} - y_{i}, x_{i} + y_{i})$

然后 $D i s (u, v) \leq D$ 就可以转化为 $max (| x_{u} - x_{v} |, | y_{u}, y_{v} |) \leq D$

这样就只需要两维 分别满足 差小于 $D$ 即可

显然这是一个 二维数点 的问题，但由于我们要知道 具体距离

而不是简单的，小于某个距离的个数，所以考虑把 树状数组 改为 std::set

我们可以考虑 二分最小距离 $D$ ，检查是否有 $\geq K$ 对点 满足条件

读入点，按 横坐标排序，扫描线扫横轴，std::queue 维护当前 横坐标区间

不合法的点（ $x < x_{i} - D$ ）弹出队列，同时从下面的 std::set 中删除

当扫到一个点 $(x_{i}, y_{i})$ 时，合法的横坐标是 $[x_{i} - D, x_{i}]$ ，避免算重

注意到 std::queue 是按 $x$ 排序的，std::set 按 $y$ 排序

删除的时候 能保证删对？std::set 中的点 按两维排序 即可，代码显然

然后放一个 std::set 维护 所有满足横坐标限制的点，按 纵坐标排序

然后每次 二分找到纵坐标 $\geq y_{i} - D$ 的点，向上遍历到纵坐标 $\leq y_{i} + D$

全部 暴力加入答案，总点数 $\geq K$ 时 立即返回，保证 时间复杂度合理

最后设第 $K$ 大距离为 $L$ ，那么先把所有距离 $\leq L - 1$ 的距离输出

然后用 $L$ 补齐即可（因为所有距离 $\leq L$ 的点对就可能不止 $K$ 个了）

代码十分简单，细节少

#include <bits/stdc++.h>

const int MAXN = 250005;

using namespace std;

struct Node1 {
	long long x, y;
	
	inline bool operator < (const Node1 &a) const {
		return x == a.x ? y < a.y : x < a.x;
	}
} P[MAXN];

struct Node2 {
	long long x, y;
	
	inline bool operator < (const Node2 &a) const {
		return y == a.y ? x < a.x : y < a.y;
	}
};

long long C;
long long Ans[MAXN];
int N, K;

inline bool Check (const long long x) {
	C = 0;
	multiset <Node2> S;
	queue <Node1> Q;
	for (int i = 1; i <= N; ++ i) {
		while (!Q.empty () && P[i].x - Q.front ().x > x) 
			S.erase (S.find ((Node2) {Q.front ().x, Q.front ().y})), Q.pop ();
		auto it = S.lower_bound ((Node2) {(P[i].x - x), (P[i].y - x)});
		while (it != S.end () && (* it).y <= P[i].y + x) {
			Ans[++ C] = max (abs (0ll + P[i].x - (* it).x), abs (0ll + P[i].y - (* it).y)), ++ it;
			if (C >= K) return 1;
		}
		S.insert ({P[i].x, P[i].y}), Q.push (P[i]);
	}
	return 0;
}

inline void Solve () {
	long long L = 1, R = 4e9, M;
	while (R > L) {
		M = L + ((R - L) >> 1);
		if (Check (M)) R = M;
		else L = M + 1;
	}
	
	Check (L - 1);
	
	sort (Ans + 1, Ans + C + 1);
	
	for (int i = 1; i <= C; ++ i) cout << Ans[i] << '\n';
	
	for (int i = C + 1; i <= K; ++ i) cout << L << '\n';
}

long long x, y;

int main () {
	
	ios::sync_with_stdio(0);
	cin.tie(0), cout.tie(0);
	
	cin >> N >> K;
	
	for (int i = 1; i <= N; ++ i) cin >> x >> y, P[i] = {x - y, x + y};
	
	sort (P + 1, P + N + 1);
	
	Solve ();
	
	return 0;
}

Luogu P4216 [SCOI2015] 情报传递

树上 单点修改（且每个点只会被 修改一次），询问路径上权值 $\leq K$ 的 节点数量

考虑由于 每个人只会被启动一次，给一个权值

所以可以先把权值（每个人启动的时刻）离线，建树，避免后面修改

这里可以想到和 Luogu P3302 [SDOI2013] 森林一样的 $t r i c k$

即 每个节点基于父亲版本 修改，然后 树上差分询问

这里建的是 可持久化权值线段树，每个点 建立一个版本，插入对应权值

查询的时候查两点 $L C A$ ，距离通过 $D e p_{u} + D e p_{v} - 2 D e p_{L C A} + 1$ 即得

权值我们就计算一下 路径上权值小于 $N o w - C$ 的点数

直接询问 $u, v, L C A, f a_{L C A}$ 然后做差即可，详情见代码

实现是简单的，甚至 权值不用离散化，十分良心

#include <bits/stdc++.h>

const int MAXN = 200005;
const int LOGN = 40;

using namespace std;

struct Edge {
	int to, nxt;
} E[MAXN << 1];

int H[MAXN], tot;

inline void Add_Edge (const int u, const int v) {
	E[++ tot] = {v, H[u]}, H[u] = tot;
}

int N, Q;
int F[MAXN][LOGN], W[MAXN], D[MAXN];
int LOG[MAXN];

namespace PSDTree {
	struct Node {
		int L, R;
		int lc, rc;
		int s;
	} T[MAXN * LOGN];
	
	#define LC T[x].lc
	#define RC T[x].rc
	#define M ((L + R) >> 1)
	
	int RT[MAXN], Tot;
	
	inline int Cpy (const int x) {
		return T[++ Tot] = T[x], Tot;
	}
	
	inline void Maintain (const int x) {
		T[x].s = T[LC].s + T[RC].s;
	}
	
	inline int Ins (const int p, int x, const int L = 0, const int R = Q) {
		x = Cpy (x), T[x].L = L, T[x].R = R, T[x].s ++ ;
		if (L == R) return x;
		if (p <= M) LC = Ins (p, LC, L, M);
		else RC = Ins (p, RC, M + 1, R);
		return x;
	}
	
	inline int Sum (const int L, const int R, const int x) {
		if (!x || R < L) return 0;
		if (T[x].L >  R || L >  T[x].R) return 0;
		if (L <= T[x].L && T[x].R <= R) return T[x].s;
		return Sum (L, R, LC) + Sum (L, R, RC);
	}
	
	inline int Que (const int u, const int v, const int lca, const int flca, const int p) {
		return Sum (0, p - 1, u) + Sum (0, p - 1, v) - Sum (0, p - 1, lca) - Sum (0, p - 1, flca);
	}
	
	#undef M
}

using namespace PSDTree;

inline void DFS (const int x, const int f) {
	RT[x] = Ins (W[x], RT[f]), D[x] = D[f] + 1;
	for (int i = H[x]; i; i = E[i].nxt) 
		if (E[i].to != f)
			DFS (E[i].to, x);
}

inline int LCA (int u, int v) {
	if (D[u] < D[v]) swap (u, v);
	while (D[u] > D[v]) u = F[u][LOG[D[u] - D[v]]];
	if (u == v) return u;
	for (int i = 18; i >= 0; -- i)
		if (F[u][i] != F[v][i])
			u = F[u][i], v = F[v][i];
	return F[u][0];
}

int Opt[MAXN], U[MAXN], V[MAXN], C[MAXN];
int p, fp;
int Dis, Ans;

int main () {
	
	ios::sync_with_stdio(0);
	cin.tie(0), cout.tie(0);
	
	cin >> N;
	
	for (int i = 1; i <= N; ++ i) cin >> F[i][0], Add_Edge (F[i][0], i);
	
	for (int i = 2; i <= N; ++ i) LOG[i] = LOG[i >> 1] + 1;
	
	cin >> Q;
	
	for (int i = 1; i <= N; ++ i) W[i] = Q;
	
	for (int i = 1; i <= Q; ++ i) {
		cin >> Opt[i];
		if (Opt[i] == 2) cin >> C[i], W[C[i]] = i;
		else cin >> U[i] >> V[i] >> C[i];
	}
	
	DFS (1, 0);

	for (int i = 1; i <= 19; ++ i)
		for (int x = 1; x <= N; ++ x)
			F[x][i] = F[F[x][i - 1]][i - 1];
	
	for (int i = 1; i <= Q; ++ i) {
		if (Opt[i] == 1) {
			p = LCA (U[i], V[i]), fp = F[p][0];
			Dis = D[U[i]] + D[V[i]] - D[p] - D[p] + 1;
			cout << Dis << ' ' << Que (RT[U[i]], RT[V[i]], RT[p], RT[fp], i - C[i]) << '\n';
		}
	}
	
	return 0;
}

Luogu P3567 [POI2014] KUR-Couriers

主席树板子

按顺序插入序列，建立 可持久化值域线段树

树上二分 查询 区间内 当前值域数的个数是否 大于区间一半

就完了

#include <bits/stdc++.h>

const int MAXN = 500005;
const int LOGN = 60;

using namespace std;

int N, Q, P;

namespace PSDTree {
	struct Node {
		int L, R, lc, rc;
		int s;
	} T[MAXN * LOGN];
	
	#define M ((T[x].L + T[x].R) >> 1)
	
	int RT[MAXN], tot = 0;
	
	inline int Cpy (const int x) {
		return T[++ tot] = T[x], tot;
	}
	
	inline int Ins (const int p, int x, const int L = 1, const int R = N) {
		x = Cpy (x), ++ T[x].s, T[x].L = L, T[x].R = R;
		if (L == R) return x;
		if (p <= M) T[x].lc = Ins (p, T[x].lc, L, M);
		else T[x].rc = Ins (p, T[x].rc, M + 1, R);
		return x;
	}
	
	inline int Query (const int rt1, const int rt2, const int p) {
		if (T[rt2].L == T[rt2].R) return T[rt2].L;
		int SumL = T[T[rt2].lc].s - T[T[rt1].lc].s, SumR = T[T[rt2].rc].s - T[T[rt1].rc].s;
		if (SumL >= p) return Query (T[rt1].lc, T[rt2].lc, p);
		if (SumR >= p) return Query (T[rt1].rc, T[rt2].rc, p);
		return 0;
	}
	
	#undef M
}

using namespace PSDTree;

int L, R;

int main () {
	
	ios::sync_with_stdio(0);
	cin.tie(0), cout.tie(0);
	
	cin >> N >> Q;
	
	for (int i = 1; i <= N; ++ i)
		cin >> P, RT[i] = Ins (P, RT[i - 1]);
	
	for (int i = 1; i <= Q; ++ i) {
		cin >> L >> R;
		cout << Query (RT[L - 1], RT[R], ((R - L + 1) >> 1) + 1) << '\n';
	}
	
	return 0;
}

CF543E Listening to Music

确实是个套路，思路很牛，而且 卡空间的那个法子太玄妙了

考虑区间长 $M$ 是常数，可以用 区间左端点 来代替 唯一的一个的区间

注意代码中使用 $K$ 来表示 给定区间长

于是我们把 给定权值从大到小排序，考虑一个值 排序前 如果在位置 $i$

则 左端点 $l \in [i - M + 1, i]$ 代表的区间 都会被这个值贡献

于是我们把 这些区间（对应的左端点区间）插入一棵 主席树（区间加 $1$ ）

区间修改查询 的 主席树 写的比较少，但是其实实现是简单的

这里版本的 继承顺序 即 较小权值从较大权值 处继承

于是 权值 $x$ 代表的主席树就记录了

每个左端点对应区间 内 权值大于等于 $x$ 的数个数

我们要求 一些区间 中 小于 $x$ 的数个数最少的区间，求 小于 $x$ 的数个数

转化为求 大于等于 $x$ 的数个数的最大值

由于主席树上 一个点代表原序列上的一个区间

那么这个问题就转变成了 主席书上区间最大值，最后用 $M$ 减去这个值即可

然后问题来了，注意到这个题的空间只有 $64 M B$ （正解是 毒瘤分块）

而 主席树空间就很大，就点数来说，一般的主席树 这道题需要 $42 N$ 个点

实验表明，这道题的 总空间 在 $83 N \sim 84 N$ 个 int 类型左右（理论 $83.88 N$ ）

再加上 维护一堆信息，空间直接爆炸！

考虑如下方法来 减小内存

标记永久化 并 动态计算标记

inline int Ins (int x, const int l, const int r, const int L = 1, const int R = N - K + 1) {
    if (L == R) return x + 1;
    x = Cpy (x);
    if (l <= L && R <= r) return T[x].mx ++, x;
    int Tag = T[x].mx - max (LMAX, RMAX); // 计算标记
    if (l <= M) LC = Ins (LC, l, r, L, M);
    if (r >  M) RC = Ins (RC, l, r, M + 1, R);
    T[x].mx = max (LMAX, RMAX) + Tag; // 加上标记
    return x;
}

区间加 对 最大值 的影响 显然需要标记维护

但是由于 影响对整个区间有效，那么这个标记可以 永久化 当成值看待

更极端一点，标记即是 当前区间的 mx 与 子节点 mx 的差，可以 实时计算

这样就可以 在节点里少记录一个信息，省下不少空间

unsigned long long 的 按位内存分配（无需 重载运算符，十分好用）

struct Node {
    unsigned long long mx : 18, lc : 23, rc : 23;
} T[MAXN * LOGN];

这样就相当于 一个节点只开了一个 unsigned long long，然后分给 三个信息

mx 的值域为 $[0, N]$ ，lx, rc 的值域均为 $0$ 到 结点数

而 $N < 2^{18}, 40 N < 2^{23}$ （为什么 结点数 是 $40 N$ 不是 $42 N$ ，看 $3.$ ）

直接在 叶子节点 记录值，省去 $2 N$ 个结点

#define LMAX (L == M ? int (LC) : int (T[LC].mx))
#define RMAX (R == M + 1 ? int (RC) : int (T[RC].mx))
// 如果是 一般节点，最大值就是 mx，如果是 叶子节点，最大值就是 父亲的’儿子标号‘ 记录的值


PSDTree::Ins : if (L == R) return x + 1;
// 如果到叶子，直接标号 +1，这样 每一次访问到这个叶子，其父亲对应的 ’儿子标号‘ 就会 +1
// 于是这个 ’标号‘ 就相当于记录的权值，也即 mx

PSDTree::Que : if (L == R) return x;
// 查询时 直接返回标号

由于 叶子节点 没有儿子，也 无需记录标记

于是我们可以 不建立真实的叶子，也不去记录它 真正的标号

而是把 它父亲指向它标号 的这个变量 拿来直接记录它的值

由于 $N$ 次修改至多产生 $2 N$ 个（ $N ?$ ）叶子，于是就 省下了这些空间

有了以上操作，我们就可以以 $63.51 M B$ 的空间 轻松通过此题 了

上面的每一步 其实都卡的很死，十分牛

注意信息如果多一个 $N$ 倍 int 的大小，那么就 多出来 $800 K B$ 左右，寄喽！

$2^{18} = 262144$ ，也就是如果 $N$ 再 大一点，寄喽！

$2^{23} = 8388608$ ，也就是如果点数真的是 $42 N$ ，那么 $8400000$ 个点，寄喽！

$18 + 2 \times 23 = 64$ ，也就是 任意一个信息再多一位都不行，十分神秘

实现起来倒是不难，码量也很小，就是注意 不要多开数组 就行

#include <iostream>
#include <algorithm> 

const int MAXN = 200005;
const int LOGN = 40;

using namespace std;

int N, K, Q;

namespace PSDTree {
	struct Node {
		unsigned long long mx : 18, lc : 23, rc : 23;
	} T[MAXN * LOGN];
	
	int RT[MAXN], tot = 0;
	
	#define M ((L + R) >> 1)
	#define LC T[x].lc
	#define RC T[x].rc
	#define LMAX (L == M ? int (LC) : int (T[LC].mx))
	#define RMAX (R == M + 1 ? int (RC) : int (T[RC].mx))
	
	inline int Cpy (const int x) {
		return T[++ tot] = T[x], tot;
	}
	
	inline int Ins (int x, const int l, const int r, const int L = 1, const int R = N - K + 1) {
		if (L == R) return x + 1;
		x = Cpy (x);
		if (l <= L && R <= r) return T[x].mx ++, x;
		int Tag = T[x].mx - max (LMAX, RMAX);
		if (l <= M) LC = Ins (LC, l, r, L, M);
		if (r >  M) RC = Ins (RC, l, r, M + 1, R);
		T[x].mx = max (LMAX, RMAX) + Tag;
		return x;
	}
	
	inline int Que (int x, const int l, const int r, const int L = 1, const int R = N - K + 1) {
		if (L == R) return x;
		if (l <= L && R <= r) return T[x].mx;
		int Ret = 0, Tag = T[x].mx - max (LMAX, RMAX);
		if (l <= M) Ret = max (Ret, Que (LC, l, r, L, M));
		if (r  > M) Ret = max (Ret, Que (RC, l, r, M + 1, R));
		return Ret + Tag;
	}
	
	#undef M
}

using namespace PSDTree;

struct node {
	int v, id;
	
	inline bool operator < (const node &a) const {
		return v > a.v;
	}
} P[MAXN];

int L, R, Lst, x;

int main () {
	
	cin >> N >> K;
	
	for (int i = 1; i <= N; ++ i) cin >> P[i].v, P[i].id = i;
	
	sort (P + 1, P + N + 1);
	
	for (int i = 1; i <= N; ++ i) {
		L = max (1, P[i].id - K + 1), R = min (N - K + 1, P[i].id);
		RT[i] = Ins (RT[i - 1], L, R);
	}
	
	cin >> Q;
	
	for (int i = 1; i <= Q; ++ i) {
		cin >> L >> R >> x, x ^= Lst;
		x = upper_bound (P + 1, P + N + 1, node ({x, 0})) - P - 1;
		cout << (Lst = K - Que (RT[x], L, R)) << '\n';
	}
	
	return 0;
}

虽然但是，剩下的 $0.49 M B$ 来开一个 $B u f f = 5 \times 10^{4}$ 的快读还是 绰绰有余 的

# 口胡

感觉 可持久化线段树 这个东西经常用来解决

需求 两个变量上的区间 的问题，可能有点抽象

就比如上面这道题，给定 左端点区间，询问 大于等于 $x$ 这个 值域区间

本质上应当是因为 可持久化 相当于 建出了 $O (N)$ 棵树

于是 线段树 本身能 解决一个区间，然后 两棵树差分 / 二分 又能解决一个区间

如果把 $O (N)$ 棵 完整线段树 建出来是 好理解的

解决 第二区间 的问题相当于一个 多树二分 或差分

然后想想 可持久化 其实 没有改变这 $O (N)$ 棵树自身的结构

只是 把相同结构部分 合并一下（或说 只新建有改动部分）来省空间

于是确实是解决这种问题的 好方式，但是显然也有一些限制

比如考虑 一次修改 在 两区间上的改动量乘积 应当是 $O (N)$ 级别的

也就是说，一般情况下 只能改其中一个区间（靠差分等手段解决另一个）

否则容易导致 线段树上修改量 $O (\log N) \to O (N)$ ，这样就不得不 重建树

时空复杂度都会假掉，如果遇到这种东西感觉得考虑根号了

~~上述东西似乎很披风~~ 并不保证上述言论的准确性

可持久化平衡树

一般情况下还是使用 $F H Q_T r e a p$

以下 平衡树 部分，没有特殊说明即默认使用 $F H Q_T r e a p$

但是 $W B L T$ 和 替罪羊树 也是不错的选择，有时间会写（鸽

很多时候又可以用 可持久化线段树 甚至 可持久化树状数组 代替

十分神秘，于是我们先来看一道假题

Luogu P3835 【模板】可持久化平衡树

注意到 没有强制在线 的 可持久化 （通常）就是 假的可持久化

我们可以尝试建出 操作树，每个版本和对应操作 代表一个点

具体来讲把 当前版本 向 它基于的那个版本 连边，然后 $D F S$ 遍历一遍 操作树

我们在 进入某个点 的时候 执行操作，退出时撤销

显然 询问操作 无需撤销

我们就能得到 正确的结果 了

这个东西的 正确性是显然的，我们可以这么理解

由于我们 每个版本 向 它基于的版本 连了边

于是 某个版本的前继版本 一定是 该版本对应点在操作树上的祖先

当遍历到一个点时，必然 经过其祖先，也就是 执行了前面版本的操作

于是此时的状态正好是 正常顺序维护时 到达该版本时的状态

然后退出时，消除这个版本的影响即可

上面讲了 如何消除可持久化的影响，于是后面就只剩 普通平衡树 的维护了

显然，这个时候写平衡树就 太没必要了

~~又长，又慢，又难写，空间还大~~

我们可以先离散化权值，然后采用 权值树状数组 或 权值线段树 实现

这里给出 权值树状数组 的实现，一般见的比较少

唯一要注意的点在于 查询排名为 $k$ 的数 时的 树状数组上二分

其实和 线段树二分 相似，我们在树状数组上 枚举每一位

判断是否能取到，取到的话就使 $k$ 减去 满足当前情况的数的数量

讲解抽象的话就看实现，只有一行，十分好写

#include <bits/stdc++.h>

const int MAXN = 524288;
const int LOGN = 18;

using namespace std;

int N, Now;

namespace BIT {
	#define lowbit(x) (x & -x)
	
	int T[MAXN];
	
	inline void Add (int x) {
		while (x <= Now) ++ T[x], x += lowbit (x);
	}
	
	inline void Del (int x) {
		while (x <= Now) -- T[x], x += lowbit (x);
	}
	
	inline int Sum (int x) {
		int Ret = 0;
		while (x) Ret += T[x], x -= lowbit (x);
		return Ret;
	}
	
	inline int Que (int x) {
		int Ret = 0;
		for (int i = (1 << LOGN); i; i >>= 1) 
			if ((Ret | i) <= Now && T[Ret | i] <= x) x -= T[Ret |= i]; // There
		return Ret;
	}
}

struct Edge {
	int to, nxt;
} E[MAXN];

int H[MAXN], tot;

inline void Add_Edge (const int u, const int v) {
	E[++ tot] = {v, H[u]}, H[u] = tot;
}

int Ver;
int Vis[MAXN];
short Opt[MAXN];
int Val[MAXN], Uni[MAXN], Ans[MAXN];

inline int Solve (const int opt, const int x) {
	
	using namespace BIT;
	
	if (opt == 2 && !Vis[x]) return 0;
	
	if (opt == 1) return Add (x), Vis[x] ++, 1;
	if (opt == 2) return Del (x), Vis[x] --, 1;
	if (opt == 3) return Sum (x - 1);
	if (opt == 4) return Que (x) + 1;
	if (opt == 5) return Que (Sum (x - 1) - 1) + 1;
	if (opt == 6) return Que (Sum (x)) + 1;
	
	return 0;
}

inline void DFS (const int x, const int f) {
	
	if (Opt[x] <= 3) Ans[x] = Solve (Opt[x], Val[x]); 
	else Ans[x] = Uni[Solve (Opt[x], Val[x])];
	
	for (int i = H[x]; i; i = E[i].nxt)
		if (E[i].to != f) DFS (E[i].to, x);
	
	if (Opt[x] == 1) Solve (2, Val[x]);
	if (Opt[x] == 2 && Ans[x]) Solve (1, Val[x]);
}

int main () {
	
	ios::sync_with_stdio(0);
	cin.tie(0), cout.tie(0);
	
	cin >> N;
	
	for (int i = 1; i <= N; ++ i) {
		cin >> Ver >> Opt[i] >> Val[i];
		if (Opt[i] != 4) Uni[++ Now] = Val[i];
		Add_Edge (Ver, i);
	}
	
	Uni[++ Now] = - 2147483647;
	Uni[++ Now] = + 2147483647;
	
	sort (Uni + 1, Uni + Now + 1);
	
	Now = unique (Uni + 1, Uni + Now + 1) - Uni - 1;
	
	for (int i = 1; i <= N; ++ i)
		if (Opt[i] != 4) 
			Val[i] = lower_bound (Uni + 1, Uni + Now + 1, Val[i]) - Uni;
	
	BIT::Add (1), BIT::Add (Now), DFS (0, 0);
	
	for (int i = 1; i <= N; ++ i)
		if (Opt[i] > 2) cout << Ans[i] << '\n';
	
	return 0;
}

容易发现 树状数组常数较小，于是加上快读的我们拿到了最优解

可持久化线段树的实现可以看 $z hicheng$

Luogu P5055 【模板】可持久化文艺平衡树

注意非常恶心的一个问题：输入会爆 int

题目只保证了 异或后的真实值 的值域

总算是一个 真正的 可持久化了...

在 Luogu P3391 【模板】文艺平衡树的基础上，这道题是简单的

我们只需要修改 关键操作，使得其在修改时复制节点即可

具体来说，我们新增一个复制结点的操作 FHQ_Treap::Cpy，与 可持久化线段树 相似

inline int Cpy (const int x) {
	return T[++ tot] = T[x], tot;
}

然后将 可能对树形态有修改的 FHQ_Treap::Update 与 FHQ_Treap::Split 操作对应变化

这里为什么 FHQ_Treap::Merge 不算修改形态？

因为 未被 Merge 的树 仅作为 一个操作的中间形态 出现

也就是不存在任意操作使得 做完这个操作之后 树还没有被 Merge

所以拷贝 Merge 之前的状态是 无意义的

我们在每次 修改形态之前拷贝版本，对于 Update，自然是 反转前 复制

inline void Update (const int x) {
    if (T[x].rev) {
        if (LC) LC = Cpy (LC); // Copy LeftChild
        if (RC) RC = Cpy (RC); // Copy RightChild
        swap (LC, RC), T[x].rev = 0; // Swap NewChild
        if (LC) T[LC].rev ^= 1;
        if (RC) T[RC].rev ^= 1;
    }
}

对于 Split，在 向下走前 复制

inline void Split (int x, const int s, int &rt1, int &rt2) {
    if (!x) return rt1 = rt2 = 0, void ();
    Update (x);
    if (T[LC].s < s) x = rt1 = Cpy (x), /* There */ Split (RC, s - T[LC].s - 1, RC, rt2), Maintain (rt1);
    else x = rt2 = Cpy (x), /* There */ Split (LC, s, rt1, LC), Maintain (rt2);
}

注意一个 十分重要的问题，考虑如果我们 每次复制新节点

复制出来的 随机权值 是和 源节点 一样的，当 大量基于同一版本复制 时

显然我们会出现 大量随机权值相等的点，这会对 平衡性产生破坏

也就是如果直接这样复制随机权值，复杂度是错误的

而由于权值又代表了 子树的合并顺序

所以随便给新点赋一个新的随机权值又会导致 树的结构错误

实际效果是 答案正确 但 新建点多了一大堆

是因为这样的话 子树需要重新合并，导致 最劣时 相当于 重构，复制了整个子树？

可能需要 巨佬教教

于是我们得想出一种 新的随机合并方式

并保证它 不会因为某个节点的复制 而必须重构整个子树

考虑 不维护随机权值，而在每次 Merge 的时候 根据子树大小 随机合并

具体来说，将 T[x].r > T[y].r 改为 rd () % (T[x].s + T[y].s) + 1 <= T[x].s

注意 rd () 出来会是 unsigned int 类型

直接转 int 再取模或不取模均可能会导致 左边出现异常负数

右边显然是正的，左边经常负的话就不平衡了

所以在 取模完了之后 再转即可，具体 FHQ_Treap::Merge 实现如下

inline int Merge (const int x, const int y) {
    if (!x || !y) return x | y;
    if ((int) (rd () % (T[x].s + T[y].s)) + 1 <= T[x].s) return Update (x), T[x].rc = Merge (T[x].rc, y), Maintain (x);
    else return Update (y), T[y].lc = Merge (x, T[y].lc), Maintain (y);
}

然后其他操作 正常执行 就行，注意到这个题需要 多维护一个区间和

FHQ_Treap::Maintain 中和 子树大小 一起更新即可

贴个部分代码

namespace FHQ_Treap {
	struct Node {
		int v, s, lc, rc;
		int rev;
		long long sum = 0;
		
		inline void Clr () {
			sum = v = s = lc = rc = rev = 0;
		} 
	} T[MAXN * LOGN];
	
	#define LC T[x].lc
	#define RC T[x].rc
	
	int RT[MAXN], Cnt = 0;
	int rt = 0, tot = 0;
	
	inline int New (const int x) {
		return T[++ tot] = {x, 1, 0, 0, 0, x}, tot;
	}
	
	inline int Cpy (const int x) {
		return T[++ tot] = T[x], tot;
	}
	
	inline int Maintain (const int x) {
		T[x].s = T[LC].s + T[RC].s + 1;
		T[x].sum = T[LC].sum + T[RC].sum + T[x].v;
		return x;
	}
	
	inline void Update (const int x) {
		if (T[x].rev) {
			if (LC) LC = Cpy (LC);
			if (RC) RC = Cpy (RC);
			swap (LC, RC), T[x].rev = 0;
			if (LC) T[LC].rev ^= 1;
			if (RC) T[RC].rev ^= 1;
		}
	}
	
	inline void Split (int x, const int s, int &rt1, int &rt2) {
		if (!x) return rt1 = rt2 = 0, void ();
		Update (x);
		if (T[LC].s < s) x = rt1 = Cpy (x), Split (RC, s - T[LC].s - 1, RC, rt2), Maintain (rt1);
		else x = rt2 = Cpy (x), Split (LC, s, rt1, LC), Maintain (rt2);
	}
	
	inline int Merge (const int x, const int y) {
		if (!x || !y) return x | y;
		if ((int) (rd () % (T[x].s + T[y].s)) + 1 <= T[x].s) return Update (x), T[x].rc = Merge (T[x].rc, y), Maintain (x);
		else return Update (y), T[y].lc = Merge (x, T[y].lc), Maintain (y);
	}
	
	inline void Ins (const int p, const int v, int x = 0, int y = 0) {
		Split (rt, p, x, y), rt = Merge (Merge (x, New (v)), y);
	}
	
	inline void Del (const int p, int x = 0, int y = 0, int z = 0) {
		Split (rt, p, x, y), Split (x, p - 1, x, z), rt = Merge (x, y);
	}
	
	inline void Rev (const int L, const int R, int x = 0, int y = 0, int z = 0) {
		Split (rt, L - 1, x, y), Split (y, R - L + 1, y, z);
		T[y].rev ^= 1;
		rt = Merge (x, Merge (y, z));
	}
	
	inline long long Sum (const int L, const int R, int x = 0, int y = 0, int z = 0, long long Ans = 0) {
		Split (rt, L - 1, x, y), Split (y, R - L + 1, y, z);
		Ans = T[y].sum;
		rt = Merge (x, Merge (y, z));
		return Ans;
	}
}

posted @ 2024-05-03 21:55 FAKUMARER 阅读(22) 评论(0) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

相关博文：

· 树上差分等操作

· 什么东西？DS！

· 可持久化线段树

· [算法学习笔记] 线段树

· 可持久化数据结构

阅读排行：
· winform 绘制太阳，地球，月球运作规律
· TypeScript + Deepseek 打造卜卦网站：技术与玄学的结合
· AI 智能体引爆开源社区「GitHub 热点速览」
· Manus的开源复刻OpenManus初探
· 写一个简单的SQL生成工具

公告

昵称： FAKUMARER
园龄： 1年5个月
粉丝： 10
关注： 26

+加关注

2025年3月

日

一

二

三

四

五

六

FAKUMARER

可持久化树

可持久化

可持久化线段树

Luogu P3919 【模板】可持久化线段树 1（可持久化数组）

Luogu P3834 【模板】可持久化线段树 2

Luogu P5795 [THUSC2015] 异或运算

Luogu P2839 [国家集训队] middle

CF464E The Classic Problem

Luogu P3302 [SDOI2013] 森林

Luogu P7561 [JOISC 2021 Day2] 道路の建設案 (Road Construction)

Luogu P4216 [SCOI2015] 情报传递

Luogu P3567 [POI2014] KUR-Couriers

CF543E Listening to Music

# 口胡

可持久化平衡树

Luogu P3835 【模板】可持久化平衡树

Luogu P5055 【模板】可持久化文艺平衡树

公告

搜索

常用链接

我的标签

合集

随笔分类

随笔档案

阅读排行榜

评论排行榜

推荐排行榜

最新评论