外向树

外向树(扫描线)

题意

给定一个n节点的外向树(每条边都是有向边且由父节点指向子节点),根为1

给出n-1条边(u,v)表示u,v之间有连边,不保证u为v父节点

给出m组询问,每次询问最少要加多少条有向边才能让编号[l,r]之间两两可达

n,m范围都是1e5

分析

1.虚树

首先很自然的将[l,r]的点抽象出来成虚树森林(建议自己手画一下).

讨论最简单的情况如果刚好是一颗虚树而不是虚树森林.

这时候我们发现只要树的叶子节点往根节点连边就可以保证一条链全都两两可达,同时可达其他与根节点有连边的节点,那么问题很显然了,对于一棵树的情况我们只需要让所有的叶子节点统一向根节点连边即可.这时候最少连边数为叶子个数

拓展到整个虚树森林,我们发现只要所有的叶子统一向原本树的根节点(即1节点)连边即可.

2.左右最近节点

将这个问题抽象成找虚树叶子节点之后,我们要进行下一步思考

什么点会是虚树的叶子节点,肯定是子节点都不在[l,r]范围内的点

并且进一步缩小范围,我们设一个点的叶子节点编号为x

k1为编号小于他的并且离他最近的节点

k2为编号小于他的并且离他最近的节点

那么我们可以将叶子节点的需求表达为$$~~k1 < l \leq x \leq r <k2 $$

3.扫描线/三维数点(cdq分治)

接下来看到这个式子之后我们就可以很明显的发现如果我们能够预处理k1和k2出来,这就是一个三维数点问题,直接用cdq分治来解决.

或者如果我们注意力再集中一点(提升注意力网站),我们可以发现如果我们将(l,r)视为一个二维平面上的点,要求l在(k1,x]范围内,r在[x,k2)范围内,也就是下图蓝色区域,我们就可以计算他的贡献

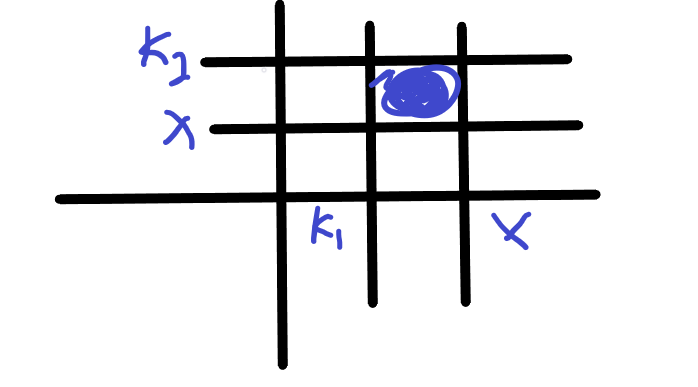
现在,我们有所有的x,和x对应的k1,k2,我们就可以算出所有矩形长什么样,这时候问题就转变成了(l,r)这个点在多少个矩形内了.

我们将问题拆分成事件和询问,并用一个数组记着,接下来用扫描线从x轴负无穷往正无穷扫,就能得出答案

4.预处理k1,k2

预处理k1,k2这个事情相对来说比较简单.

首先我们注意到一个子树内的dfn序是连续的,我们先dfs记录进入所有点的时间戳以及离开所有点的时间戳,接下来我们根据编号依次查询点,加入点,用线段树维护

每次查询大体为query(1, 1, n, in[i], out[i]) (因为子树连续,查询进入和出去时间)

每次更新大体为update(1,1,n,in[i],i),表示把dfn序比in[i]小的编号全部与i取min或max

5.代码

#include <bits/stdc++.h>
using namespace std;
#define int long long
typedef long long ll;
typedef long double ld;
#define endl '\n'
#define pii pair<int, int>
#define cerr                                                                                                           \
    if (test) cerr
#define freopen                                                                                                        \
    if (test) freopen
#define whtest if (test)
const int test = 1;
const int N = 2e5 + 10;
const int mod = 998244353;
const int inf = 0x3f3f3f3f3;
const ll inff = 1ll << 60;
inline int read() {
    int x;
    cin >> x;
    return x;
}
struct seg {
#define lu u << 1
#define ru u << 1 | 1
    vector<int> val;
    int flag;
    seg(int m, int val, int op) : val(m, val), flag(op) {
    }
    void update(int u, int l, int r, int x, int v) {
        if (l == r) {
            val[u] = v;
            return;
        }
        int mid = l + r >> 1;
        if (x <= mid) update(lu, l, mid, x, v);
        else update(ru, mid + 1, r, x, v);
        if (flag == 1) val[u] = max(val[lu], val[ru]);
        else val[u] = min(val[lu], val[ru]);
    }
    int query(int u, int l, int r, int x, int y) {
        if (x <= l && r <= y) return val[u];
        int mid = l + r >> 1;
        int res = 0;
        if (flag == 1) {
            res = 0;
            if (x <= mid) res = max(res, query(lu, l, mid, x, y));
            if (y > mid) res = max(res, query(ru, mid + 1, r, x, y));
        } else {
            res = inf;
            if (x <= mid) res = min(res, query(lu, l, mid, x, y));
            if (y > mid) res = min(res, query(ru, mid + 1, r, x, y));
        }
        return res;
    }
};


struct BIT {
    vector<int> a;
    int n;
    BIT(int m) : n(m), a(m, 0){};
    void init(int s) {
        for (int i = 1, n = s; i <= n; i++) a[i] = 0;
    }
    int lowbit(int x) {
        return x & -x;
    }
    void update(int p, int x) {
        for (; p <= n; p += lowbit(p)) a[p] += x;
    }
    int query(int p) {
        int res = 0;
        for (; p; p -= lowbit(p)) res += a[p];
        return res;
    }
    int query(int l, int r) {
        return query(r) - query(l);
    }
    int kth(int k) { // kth(k)结果为第一个满足qry(0,p)=k的p
        if (!n) return 0;
        int x = 0;
        for (int i = 1 << __lg(n); i; i /= 2) {
            if (x + i <= n && k >= a[x + i - 1]) {
                x += i;
                k -= a[x - 1];
            }
        }
        return x;
    }
};
BIT c(N);
vector<array<int, 3>> b[N];

void solve() {
    int n = read(), m = read();
    vector e(n + 1, vector<int>());
    seg s1(N << 2, 0, 1), s2(N << 2, n + 1, 0);//s1求左边最近,s2右边最近,两个线段树内部不完全一样,一个是取min一个是max
    vector<int> l(n + 1), r(n + 1);
    for (int i = 1; i < n; i++) {
        int u = read(), v = read();
        e[u].push_back(v), e[v].push_back(u);
    }
    vector<int> in(n + 1), out(n + 1);
    {//处理dfn
        int cnt = 0;
        auto dfs = [&](auto self, int u, int fa) -> void {
            in[u] = ++cnt;
            for (auto v : e[u]) {
                if (v == fa) continue;
                self(self, v, u);
            }
            out[u] = cnt;
        };
        dfs(dfs, 1, 0);
    }
    for (int i = 1; i <= n; i++) {//求左边最近
        l[i] = s1.query(1, 1, n, in[i], out[i]);
        s1.update(1, 1, n, in[i], i);
    }

    for (int i = n; i >= 1; i--) {//求右边最近
        r[i] = s2.query(1, 1, n, in[i], out[i]);
        s2.update(1, 1, n, in[i], i);
    }

    for (int i = 1; i <= n; i++) {//扫描线部分的事件
        b[l[i] + 1].push_back({i, r[i] - 1, 1});
        b[i + 1].push_back({i, r[i] - 1, -1});
    }

    vector<pii> d[n + 1];
    vector<int> ans(m + 1);

    for (int i = 1; i <= m; i++) {//扫描线部分的查询
        int x = read(), y = read();
        d[x].push_back({y, i});
    }

    for (int i = 1; i <= n; i++) {
        for (auto [x, y, v] : b[i]) {//树状数组直接维护一个区间的加
            c.update(x, v),c.update(y + 1, -v);
        }
        for (auto [j, id] : d[i])//如果问的点不是自己这个点,就记录查询的编号
            if (i != j) ans[id] = c.query(j);
    }
    for (int i = 1; i <= m; i++) {
        cout << ans[i] << endl;
    }
}

signed main() {
    freopen("in.txt", "r", stdin);
    freopen("out.txt", "w", stdout);
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    int t = 1;
    while (t--) {
        solve();
    }
    return 0;
}