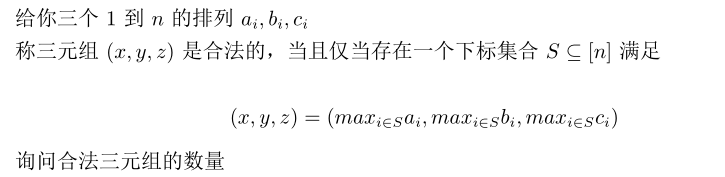Jzoj5608 Subset
这道题非常有意思
首先我们可以发现,对于一个合法的三元组我们可以找到一个大小小于3的下标集合S与之对应
那么我们就来考虑找到所有合法的这样的S
当|S|=1时,显然都是成立的
当|S|=2时,我们只需要保证s中两个元素i,j不满足a[i]<a[j],b[i]<b[j],c[i]<c[j]就可以了
考虑计算不满足的方案,可以用cdq分治+fenwick完成
当|S|=3时,我们直接计算比较困难,我们考虑两种不合法的情况
1.存在一个元素x满足a[x],b[x],c[x]都是最大的
2.存在一个元素x满足a[x],b[x],c[x]中有两个是最大的
对于第一种情况,我们可以沿用计算|S|=2时的结果,乘上一个组合数,设这部分的答案为A
对于第二种情况,我们可以考虑容斥,先设这部分的答案为B
让后我们可以考虑计算对于一个元素x,a[x],b[x],c[x]存在至少两个是最大的
直接枚举哪两个是最大的让后按照其中一个排序,另一个用fenwick维护
那么设这样计算的答案为X,显然有X=A*3+B 那么我们就得到了B
用总方案数减掉A和B就是|S|=3时的答案
好题!
#pragma GCC optimize("O3")
#pragma G++ optimize("O3")
#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
int n,m,w[100010]; long long A,B,X,S=0;
struct dt{ int a,b,c,G; } s[100010],b[100010];
inline bool c1(dt a,dt b){ return a.a<b.a; }
inline bool c2(dt a,dt b){ return a.b<b.b; }
void cdq(int l,int r){
if(l==r) return;
int m=l+r>>1,i,j,t=l,a=s[m].a;
cdq(l,m); cdq(m+1,r);
for(i=l,j=m+1;i<=m && j<=r;)
if(s[i].b<s[j].b){
for(int x=s[i].c;x<=n;x+=x&-x) ++w[x];
b[t++]=s[i++];
} else {
for(int x=s[j].c;x;x&=x-1) s[j].G+=w[x];
b[t++]=s[j++];
}
for(;i<=m;){
for(int x=s[i].c;x<=n;x+=x&-x) ++w[x];
b[t++]=s[i++];
}
for(;j<=r;){
for(int x=s[j].c;x;x-=x&-x) s[j].G+=w[x];
b[t++]=s[j++];
}
for(;l<=r;++l){
s[l]=b[l];
if(s[l].a<=a)
for(int x=s[l].c;x<=n;x+=x&-x) --w[x];
}
}
int main(){
freopen("subset.in","r",stdin);
freopen("subset.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n;++i) scanf("%d",&s[i].a);
for(int i=1;i<=n;++i) scanf("%d",&s[i].b);
for(int i=1;i<=n;++i) scanf("%d",&s[i].c);
sort(s+1,s+1+n,c1); cdq(1,n);
for(int i=1;i<=n;++i) A+=(s[i].G*(s[i].G-1ll)>>1);
sort(s+1,s+1+n,c1);
int w[100010]={0};
for(int i=1,j,t;i<=n;++i){
for(t=0,j=s[i].b;j;j&=j-1) t+=w[j];
for(j=s[i].b;j<=n;j+=j&-j) w[j]++;
X+=t*(t-1ll)>>1;
}
memset(w,0,sizeof w);
for(int i=1,j,t;i<=n;++i){
for(t=0,j=s[i].c;j;j&=j-1) t+=w[j];
for(j=s[i].c;j<=n;j+=j&-j) w[j]++;
X+=t*(t-1ll)>>1;
}
sort(s+1,s+1+n,c2);
memset(w,0,sizeof w);
for(int i=1,j,t;i<=n;++i){
for(t=0,j=s[i].c;j;j&=j-1) t+=w[j];
for(j=s[i].c;j<=n;j+=j&-j) w[j]++;
X+=t*(t-1ll)>>1;
}
B=X-A*3; S=n*(n+1ll)>>1;
for(int i=1;i<=n;++i) S-=s[i].G;
S+=n*(n-1ll)*(n-2ll)/6; S-=A+B;
printf("%lld\n",S);
}