【游记】重生之 CSP 2022 卷土重来
CSP 2022 游记
\(\text{Day }1\) 前面到底是 \(\text{Day }0\) 还是 \(\text{Day }-1\)??
\(\text{Day }-2\)
打了场模拟赛,感觉状态不错。总和之前的模拟赛经验,发现只要不被 T1 创死发挥都可以。
\(\text{Day }-1\)
上午做了一下之前集训讲的题,一直写到了下午 \(3\) 点,然后就开摆了。
\(\text{Day }1\)
上午
上午考 J 组,我们学校就是考场,而我们的备考室就在考场旁边。教练给我们发了 J 组的题目,并让我们造数据。
简单评价一下 J 组:T1,T2 的难度其实不坏,T3 放一道表达式求值的板子还是略显敷衍,T4 的 dp 很恰当。
感觉也没有什么需要复习的,就等着下午考试了。
中午
提前买了一瓶矿泉水和一支士力架。午觉睡得很香。
下午
终于要开考了,考前调整了一下心态,然后在考前 \(15\mathrm{min}\) 进考场。
今年打算整点花活,用 \(\text{NOI Linux}\) 写代码。去年我旁边的人就这么干的,今年我也变成了这样。
开考后花了大约 \(7\mathrm{min}\) 配完了 Code::Blocks 并写完了简洁版 FastIO,然后开始看题。
T1 holiday
题意:给出一张无向图和常数 \(k\),点有点权,求一条路径 \(1\leadsto A\leadsto B\leadsto C\leadsto D\leadsto 1\) 使得 \(A,B,C,D\) 互不相同且相邻的点距离不超过 \(k\),并最大化 \(A,B,C,D\) 点权和。\(n\le 2500,\ m\le 10000,\ k\le 100\)。
看了一会就发现一个点能到达的点可以直接 BFS 出来。然后打算做四遍 DP,但是又不好处理不重复。
接着发现这个路径好像很对称,就往折半想。然后发现可以预处理出 \(O(n^2)\) 个点对,然后枚举 \(B,C\),因为抽屉原理,所以只需要再枚举它们对应的前 \(3\) 大的 \(A,D\) 就行了。
好像过题了。十分感动。没被创死。
接着写代码,由于不习惯 \(\text{Linux}\),加上虚拟机不知道为什么比较卡,又犯了几个神必错误,\(40\mathrm{min}\) 左右才过。
T2 game
题意:给出序列 \(a,b\),\(q\) 次询问,Alice 选出一个 \(x\in[l_1,r_1]\),Bob 选出一个 \(y\in[l_2,r_2]\),Alice 希望最大化 \(a_xb_y\),Bob 则希望最小化。求最后的 \(a_xb_y\)。\(n,m,q\le 10^5,\ a_i,b_i\le 10^9\)。
感觉挺离谱的,开始以为 Alice 和 Bob 只会选最值。于是哐哐哐码了一个 ST 表,然后调试的时候被 \(\text{NOI Linux}\) 的神必不能复制文本的终端整蚌埠,最后样例 \(1\) 挂了。
然后发现两人还可以选 \(0\),于是打了一下补丁,接着样例 \(2\) 挂了。
仔细观察后,终于得到正确结论:两人的有用决策只有正数的 \(\min/\max\),负数的 \(\min/\max\),以及 \(0\)。然后码码码,在 \(\mathrm{1h30min}\) 左右过了大样例。这是全场最强大样例。
T3 galaxy
题面太长,懒得看,感 觉 很 复 杂,先看 T4。
T4 transmit
题意:给出一棵树,你一次可以跳到距离自己不超过 \(k\) 的节点,\(q\) 次询问求从 \(u\) 跳到 \(v\) 的最小点权和。\(n,q\le 2\times 10^5,\ k\le 3\)。
边吃士力架边想。感觉这题需要流畅的写代码环境,于是退出了(卡顿的) \(\text{Linux}\)。
先想了想序列的做法,发现可以用一个 DP:\(f_i=\min_{j=1}^k\{f_{i-j}+a_i\}\)。这个 DP 貌似是可以写成 \(\min,+\) 矩阵乘法的,那就可以直接搬到树上倍增维护了,LCA 还可以往上跳,讨论一下。于是开码,不久后过了样例 \(1\),然后样例 \(2\) 挂了。
思考一下,发现可以跳进某个点的子树……突然又不会了,回去看 T3。
T3 galaxy(拷贝)
题意:给出一张有向图,每次操作摧毁/修复一条边或者摧毁/修复一个点的所有入边。操作后输出保留没被摧毁的边,图是不是一棵基环内向树森林。
这次静下心来看题,题意一眼顶针,既然如此,判断出度为 \(1\) 的点数就行了呀。于是码码码,不久后过了全部大样例。这个东西有高达 \(50\) 的部分分。
此时离比赛结束还有 \(1\mathrm{h}\)。
T4 transmit(拷贝)
我不会正解我拿暴力总行了吧。于是口胡了另一个 DP,能拿 \(n,q\le 3000\) 和随机父亲生成的树。正准备开码,发现这东西好像和之前的做法不能说是大相径庭,只能说是改改就对。
这是最后的做法:设 \(f_{i,j}\) 表示停留在 \(i\) 子树内与 \(i\) 距离为 \(j\) 的最小代价,然后预处理一下一个点往下若干深度的最小点权,可以直接写成矩阵转移。因为一个点不会先跳上再跳下(除了 LCA,要特殊讨论),而往上走和往下走有用的子树都一样(因为最小化,所以往上走的时候没必要去除自己影响)。
然后在考试结束前 \(30\mathrm{min}\) 过掉了大样例。
The End (?)
一些花絮:
- T4 发现了一个奇怪的 case 没有处理,最后 \(5\mathrm{min}\) 改掉了,考后发现由于 \(k\) 太小这种 case 不会出现。
- T1 跑得贼慢,瓶颈在于排序,结果考后发现求前 \(3\) 大根本没必要排序(当然吸了氧还是够快的)。
估分 \(100+100+50+100=350\)。我进化了!!!11
\(\text{Day }1.5\)
InfOJ 已经有四道题的民间数据了,去自测了一下,结果很难蚌。
T1,T2,T4 倒是都没挂,T3 直接挂成 \(10\) 分,请哈学长来帮忙才发现这个问题,直接放代码:
else if(opt==2)
{
read(u);
for(auto &i: rev[u])
{
if(del[i.second]) continue;
del[i.second]=true;
cnt-=(deg[i.first]==1),cnt+=((--deg[i.first])==1);
break;/**/
}
}
这么一来我就只有那没有 \(2,4\) 操作的 \(10\) 分了,挂成 \(310\)。
看到同学群里平均 \(350\),整蚌埠了。CCF 他造数据一直可以的。
The End
再来一个花絮(同学的迷惑代码):
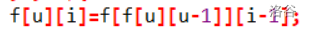
还没出分,出分后填。
2022/11/7 upd:出分啦!T1 发现了神必错误,挂了 \(5\) 分,但是 T3 又多了 \(5\) 分,所以还是 \(310\)(
同学们的分数与估分差不多,感觉总体上还行比去年进步了 \(265\) 分,CSP 2022 就告一段落啦 qwq。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号