Codeforces 817

A
你可以按如下方式移动
问能不能从给定的一个坐标走到另一个。
【solution】
裸,奇偶性注意
#include<stdio.h> #include<stdlib.h> #include<iostream> #include<string> #include<string.h> #include<algorithm> #include<math.h> #include<queue> #include<map> #include<vector> #include<set> #define il inline #define re register using namespace std; int a1,b1,a2,b2,x,y,a,b; int main(){ cin>>a1>>b1>>a2>>b2>>x>>y; if((a1-a2)%x==0&&(b1-b2)%y==0){ a=(a1-a2)/x; b=(b1-b2)/y; if((a-b)%2==0){ cout<<"YES\n"; } else cout<<"NO\n"; } else cout<<"NO\n"; return 0; }
B
After returning from the army Makes received a gift — an array a consisting of n positive integer numbers. He hadn't been solving problems for a long time, so he became interested to answer a particular question: how many triples of indices (i, j, k) (i < j < k), such that ai·aj·ak is minimum possible, are there in the array? Help him with it!
The first line of input contains a positive integer number n (3 ≤ n ≤ 105) — the number of elements in array a. The second line contains n positive integer numbers ai (1 ≤ ai ≤ 109) — the elements of a given array.
Print one number — the quantity of triples (i, j, k) such that i, j and k are pairwise distinct and ai·aj·ak is minimum possible.
【solution】
就是问成绩最小的有序三元组有多少个,排序搞定
#include<stdio.h> #include<stdlib.h> #include<iostream> #include<string> #include<string.h> #include<algorithm> #include<math.h> #include<queue> #include<map> #include<vector> #include<set> #define il inline #define re register using namespace std; typedef long long ll; const int N=1000001; int n,a[N],b[N],c[N],m; int main(){ scanf("%d",&n); for(int i=1;i<=n;i++){ scanf("%d",&a[i]);b[i]=a[i]; } sort(b+1,b+n+1); m=unique(b+1,b+n+1)-b-1; for(int i=1;i<=n;i++) a[i]=lower_bound(b+1,b+m+1,a[i])-b; for(int i=1;i<=n;i++) c[a[i]]++; if(c[1]>=3){ cout<<((ll)c[1]*(c[1]-1)*(c[1]-2)/6)<<endl; } else{ if(c[1]==2){ cout<<c[2]<<endl; } else if(c[1]==1){ if(c[2]>=2) cout<<((ll)c[2]*(c[2]-1)/2)<<endl; else cout<<c[3]<<endl; } } return 0; }
C
f(i)表示i所有数位的和
问满足 i-f(i)>=s (i<=n) 的有多少个
n,s<=10^18
【solution】
显而易见,f(i)最大也就是18*9=162,所以[s,s+1000]这个范围直接枚举,更大的肯定是满足的。
#include<stdio.h> #include<stdlib.h> #include<iostream> #include<string> #include<string.h> #include<algorithm> #include<math.h> #include<queue> #include<map> #include<vector> #include<set> #define il inline #define re register using namespace std; typedef long long ll; ll n,m,ans; il ll f(ll n){ ll res=0; for(;n;n/=10) res+=(n%10); return res; } int main(){ cin>>n>>m; for(ll i=m;i<=n&&i<=m+10000;i++){ if(i-f(i)>=m) ans++; } ans+=n-min(n,m+10000); cout<<ans; return 0; }
D
给定一个长度为n的数组a (n<=100000)
求sigma(max(i,j)-min(i,j)) (1<=i<=j<=n)
【solution】
显然的把最大和最小拆开做
我们采用分治算法解决问题
我们去除一段中最大(小)统计贡献,然后左右递归
最多递归n次,采用st算法加速
#include<stdio.h> #include<stdlib.h> #include<iostream> #include<string> #include<string.h> #include<algorithm> #include<math.h> #include<queue> #include<map> #include<vector> #include<set> #define il inline #define re register #define cmin(x,y) (a[x]<a[y]?x:y) #define cmax(x,y) (a[x]>a[y]?x:y) using namespace std; typedef long long ll; const int N=1111111; int n,s[N][21],t[N][21],a[N],k[N]; ll ans=0; il int getmin(int l,int r){ int h=r-l+1,p=r-(1<<k[h])+1; return cmin(s[l][k[h]],s[p][k[h]]); } il int getmax(int l,int r){ int h=r-l+1,p=r-(1<<k[h])+1; return cmax(t[l][k[h]],t[p][k[h]]); } il void dfs1(int l,int r){ if(l>r) return; int mid=getmin(l,r); ans-=(ll)a[mid]*(mid-l+1)*(r-mid+1); dfs1(l,mid-1);dfs1(mid+1,r); } il void dfs2(int l,int r){ if(l>r) return; int mid=getmax(l,r); ans+=(ll)a[mid]*(mid-l+1)*(r-mid+1); dfs2(l,mid-1);dfs2(mid+1,r); } int main(){ scanf("%d",&n); for(int i=1,K=0;i<=n;i++){ if((1<<K+1)<i) K++; scanf("%d",&a[i]);k[i]=K; t[i][0]=s[i][0]=i; } for(int j=1;j<=k[n];j++){ for(int i=1,k=(1<<j-1)+1;k<=n;i++,k++){ s[i][j]=cmin(s[i][j-1],s[k][j-1]); t[i][j]=cmax(t[i][j-1],t[k][j-1]); } } dfs1(1,n);dfs2(1,n); cout<<ans; return 0; }
E
维护一个正整数构成的集合p
支持三个操作
1、添加一个元素
2、删除一个已经存在的元素
3、输入x,y,询问集合中满足pi^x<y的元素有多少个。
【solution】
解法十分的巧妙,把元素转化成二进制,建立trie树,问题迎刃而解。
希望这种做法能在难题里得到应用。
#include<stdio.h> #include<stdlib.h> #include<iostream> #include<string> #include<string.h> #include<algorithm> #include<math.h> #include<queue> #include<map> #include<vector> #include<set> #define il inline #define re register using namespace std; const int N=1000001; int n=1,Q,c[N*10][2],s[N*10]; int main(){ scanf("%d",&Q); for(int ii=1,jj,x,y,h,ans;ii<=Q;ii++){ scanf("%d%d",&jj,&x);h=1; if(jj==1){ for(int i=30,j;i>=0;i--){ j=(x&(1<<i))>0; if(!c[h][j]) c[h][j]=(++n); h=c[h][j];s[h]++; } } if(jj==2){ for(int i=30,j;i>=0;i--){ j=(x&(1<<i))>0; h=c[h][j];s[h]--; } } if(jj==3){ scanf("%d",&y);ans=0; for(int i=30;i>=0;i--){ if(y&(1<<i)){ if(x&(1<<i)){ ans+=s[c[h][1]]; h=c[h][0]; } else{ ans+=s[c[h][0]]; h=c[h][1]; } } else{ if(x&(1<<i)) h=c[h][1]; else h=c[h][0]; } } printf("%d\n",ans); } } return 0; }
F
维护区间裸题
1、染黑一个区间
2、染白一个区间
3、翻转一个区间
操作后要求输出最靠左的黑点的坐标
【solution】
线段树
细节:有的标记不能简单覆盖!【以前一直忽略的!】
#include<stdio.h> #include<stdlib.h> #include<iostream> #include<string> #include<string.h> #include<algorithm> #include<math.h> #include<queue> #include<map> #include<vector> #include<set> #define il inline #define re register using namespace std; typedef long long ll; const int N=2000001; int t[N],Q,m=1,L[N],R[N],s[N],p,c[N]; ll l[N],r[N],b[N]; il int d(int a,int b){ if(a==0) return b; if(b<3) return b; return 3-a; } il void pushdown(int i){ if(t[i]==0) return; if(t[i]==1){ t[i+i]=t[i+i+1]=1; s[i+i]=R[i+i]-L[i+i]+1; s[i+i+1]=R[i+i+1]-L[i+i+1]+1; t[i]=0; } else if(t[i]==2){ t[i+i]=t[i+i+1]=2; s[i+i]=s[i+i+1]=0; t[i]=0; } else if(t[i]==3){ t[i+i]=d(t[i+i],t[i]); t[i+i+1]=d(t[i+i+1],t[i]); s[i+i]=R[i+i]-L[i+i]+1-s[i+i]; s[i+i+1]=R[i+i+1]-L[i+i+1]+1-s[i+i+1]; t[i]=0; } } il void work(int i,int p,int q,int v){ if(q<L[i]||p>R[i]) return; if(i<m) pushdown(i); if(p<=L[i]&&R[i]<=q){ if(v==1) s[i]=R[i]-L[i]+1; if(v==2) s[i]=0; if(v==3) s[i]=R[i]-L[i]+1-s[i]; t[i]=d(t[i],v); return; } work(i+i,p,q,v);work(i+i+1,p,q,v); s[i]=s[i+i]+s[i+i+1]; } il int query(int i){ if(i<m) pushdown(i); if(s[i]==0) return L[i]; if(s[i+i]<R[i+i]-L[i+i]+1) return query(i+i); else return query(i+i+1); } int main(){ scanf("%d",&Q); for(int i=1;i<=Q;i++){ scanf("%d%I64d%I64d",&c[i],&l[i],&r[i]); b[++p]=l[i];b[++p]=l[i]+1; b[++p]=r[i];b[++p]=r[i]+1; } b[++p]=1; sort(b+1,b+p+1); p=unique(b+1,b+p+1)-b-1; for(int i=1;i<=Q;i++){ l[i]=lower_bound(b+1,b+p+1,l[i])-b; r[i]=lower_bound(b+1,b+p+1,r[i])-b; } while(m<p) m<<=1; for(int i=m;i<m+m;i++) L[i]=R[i]=i-m+1; for(int i=m-1;i;i--) L[i]=L[i+i],R[i]=R[i+i+1]; for(int i=1;i<=Q;i++){ work(1,l[i],r[i],c[i]); printf("%I64d\n",b[query(1)]); } return 0; }

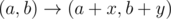

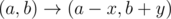


 浙公网安备 33010602011771号
浙公网安备 33010602011771号