数列分块入门1（区间加法）

原题：http://www.caioj.cn/problem.php?id=1244

题解：对于区间的所有元素加c并要求单点的值。显然可以用线段树来求，但本篇要用新的方法来求。

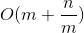
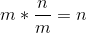
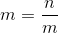
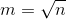
令：m为每一个块的大小，且m为根号n向下取整。每个块大小为m,共有n/m个块由于每次不完整的块大小较少，即每次操作时间复杂度为。又因根据均值不等式当时时间复杂度最少。所以每个块的大小为:。

规定：

m=sqrt(n)//每个块的大小
pos[i] //i是第几个块
sum[i] //第i个块的标记

 

对于每一组操作,先暴力处理两边的块，在个中间的块打上标记。答案就是a[i]+sum[pos[i]]

#include<cstdio>
#include<cmath>
#include<algorithm>
#define N 110000
using namespace std;
int a[N],pos[N],sum[N];
int n,m,l,r,c,opt;
inline void add(int l,int r,int c){
	for(int i=l;i<=min(r,pos[l]*m);i++) a[i]+=c;
	if(pos[l]!=pos[r])
		for(int i=(pos[r]-1)*m+1;i<=r;i++) a[i]+=c;
	for(int i=pos[l]+1;i<=pos[r]-1;i++) sum[i]+=c;
}
int main(){
//	freopen("input.in","r",stdin);
	scanf("%d",&n);m=sqrt(n);
	for(int i=1;i<=n;i++)scanf("%d",&a[i]),pos[i]=(i-1)/m+1; 
	for(int i=1;i<=n;i++){
		scanf("%d%d%d%d",&opt,&l,&r,&c);
		if(opt==1) printf("%d\n",a[r]+sum[pos[r]]);
		else add(l,r,c);
	}
	return 0;
}