万字解析DeepSeek MOE架构——从Switch Transformers到DeepSeek v1/v2/v3
前文对基于DeepSeek v3 Base模型训练的deepseek-R1技术报告进行了解读,如有需求可阅读:
前文对DeepSeek v3技术报告中的MLA进行了解析,如有需求可阅读:
正文开始前的碎碎念
写本篇的内容初衷是总结一下很长一段时间以来对于MOE架构的笔记,同时更系统的对DeepSeek的V1/V2/V3的MOE实现进行一下梳理,客观的来说,大部分内容都是之前读论文或者拜读其他大佬们文章而做的笔记,如果有存疑之处,请不吝指出。
MOE全称是Mixture of Experts,也就是混合专家模型,本人最早关注到MOE架构是23年底Mistral.AI发布的Mixtral 8*7B模型,记得当时这个模型引爆了这个AI圈对于MOE稀疏架构的关注,很多人(包括我)才开始关注到MOE架构,陆陆续续的看了一些MOE应用在Transformer架构上的相关论文,包括GShard、Switch Transformer等,现在来看,其实MOE架构存在的时间很久远,在Transformer架构没有出现之前就已经针对机器学习的模型进行过应用,最早像1991年就有《Adaptive Mixtures of Local Experts》提出了混合专家模型的雏形,其核心思想也延用至今。
本篇内容的主线是从Switch Transformer开始简单了解MOE架构,再引申到deepseek v1、v2、v3系列,内容上只关注这几篇论文中的MOE及相关的优化部分,至于其他内容就不再提及了。相关笔记在写的过程中除了论文也会参考一些其他资料,比较碎,就不一一列举了。
之所以选择上面主线内容是因为自身工作属性原因更关注密集型模型,对于MOE模型了解和使用上相对比较少,MOE这种稀疏模型更适合云计算并行推理使用,但不可否认,MOE架构在AI模型中的地位已经十分重要,其实国内Qwen、MiniMax也开源了几款不错的MOE模型,之前也关注了一些,架构实现上比DeepSeek的MOE方案更简单,包括最新开源的MiniMax-Text-01,这款模型和deepseek-R1同一时间段发布(包括kimi-1.5),但实际热度上都没有DeepSeek-R1炸裂,当然目前暂未开源的Qwen-2.5-Max也传出是MOE模型。
ok,不再废话,正文开始!
Switch Transformers: Scaling to Trillion Parameter Models with Simple and Efficient Sparsity
MOE的基本原理是使用混合专家来替代原transformer架构中的前向反馈层(FFN),在论文中的示意图如下:
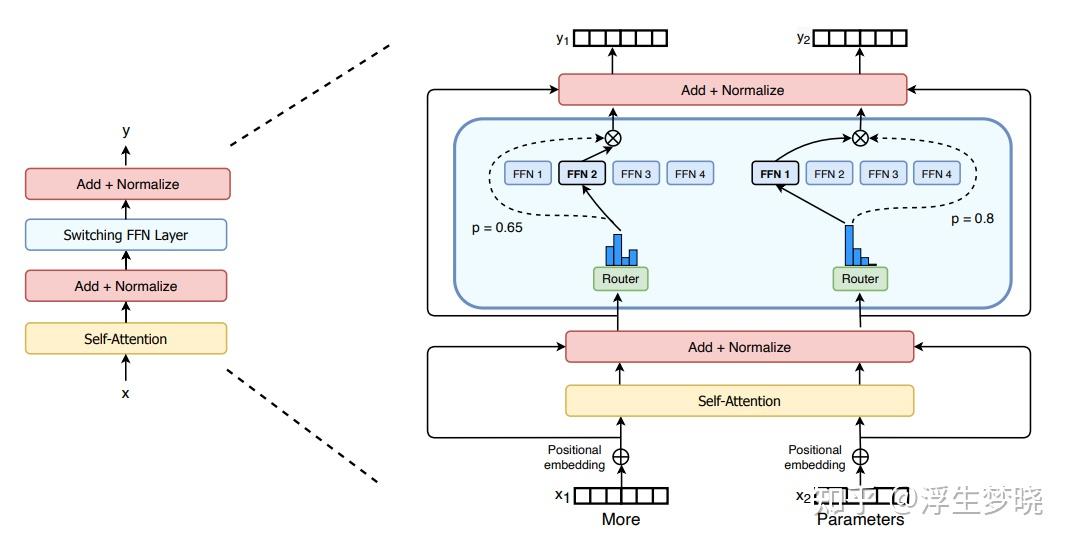
从图中可以看到,一个token输入经过Attention计算并且归一化操作后除了残差分支外,原本通向FFN层的分支进入了MOE层,简单来说,MOE层是由多个FFN组成,每个FFN理论上更关注不同领域知识,也就是所谓的专家,每个token会选择其中的top-K个FFN向前传递,即选择这个token所在领域相关的专家,这个top-K也可能是个权重系数。
总的来说,MOE层可以大致分为两个部分:路由器(路由到top-K个专家)、n个专家FFN,路由器又可以分为门控(softmax操作,选择不同专家的权重)以及选择器(选择Top-K个专家)。
Switch Transformers路由器部分
在Switch Transformers中,路由部分分为两个部分,分别是简单稀疏路由和高效稀疏路由,简单稀疏路由是针对当前token选择出一个专家 , 高效稀疏路由则是针对高效的专家并行方案设计的(关于专家并行不再详细展开,仅简单描述)。
1.简单稀疏路由:
(1).经典的混合专家路由
首先定义以下符号:
𝑁 :专家FFN的数量;
{𝐸𝑖(𝑥)}𝑖=1𝑁 :每个专家对于隐藏层激活值 𝑥 的计算;
𝑊𝑟 :每个专家的门控权重计算矩阵;
ℎ(𝑥)=𝑊𝑟⋅𝑥 :隐藏层激活值 𝑥 与每个专家门控权重矩阵计算后的logits;
因此,对于第 𝑖 个专家来说:
𝑝𝑖(𝑥)=𝑒ℎ(𝑥)𝑖∑𝑗𝑁𝑒ℎ(𝑥)𝑗 代表专家 𝑖 的门控权重系数。
𝑇 :选择的Top-K个专家数量,则:
𝑦=∑𝑖∈𝑇𝑝𝑖(𝑥)𝐸𝑖(𝑥) 代表该层的输出,即 𝑇 个专家的加权输出。
(2).Switch 路由:重新思考专家混合
上面1中的方案是比较传统的MOE方案,一般情况下都会选择 𝑇 >1,但是在Switch Transformers中却选择了Top-K=1,即上面公式中的 𝑇 为1,这样做的原因时考虑到专家并行方案时的通信、计算以及存储因素。
这里简单描述一下专家并行,其实原理十分简单,由于MOE层有多个专家(假设16个),如果我们有16张卡,那么在设计并行方案时对于MOE层就可以天然的将不同的专家分组放到不同的卡上(这里每个卡可以有1个专家)。对于非MOE层则可以使用张量并行、序列并行等其他高效方案。
参考下图:
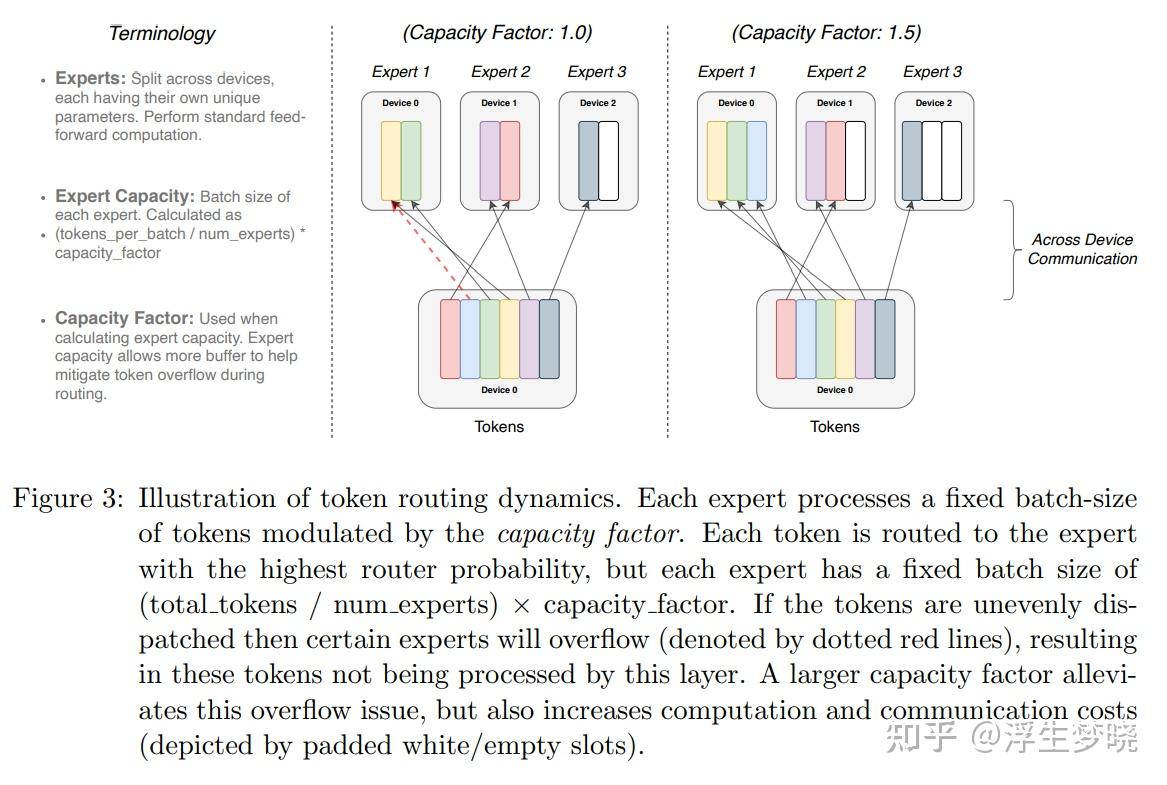
在图中可以发现,当使用专家并行方案时,为了满足分布式中计算、通信、存储的平衡,使用Top-K=1的MOE方案会更加高效,这样对于同一个批次的token来说,不同的token会划分到不同的专家上。这里定义了一个参数叫做capacity_factor(容量因子),容量因子控制这每个专家可以处理的token数量,专家容量计算为(total_tokens / num_experts)* capacity_factor,在上图左侧apacity_factor=1.0中可以看到,假设有6个token,3个专家时,这时apacity_factor=1.0使得每个专家只能处理2个token,当红色虚线部分想给专家1多分配一个token时会发现专家1没有多余的容量去处理这个token,这样也就造成了溢出,那么这个没有专家处理的token就直接残差绕过了这一层的MOE。当apacity_factor=1.5时,每个专家容量变成了3,这样每个token都会有专家来处理。
这里提一点,之前说到Switch Transformers中选择了Top-K=1是多方面的平衡,可以参考上图,如果一个token选择多个专家进行计算,则分布式通信、存储会变得十分复杂。
2.高效稀疏路由
仅使用上面的简单稀疏路由会带来一定的问题,最大的问题就是训练和推理时token会集中的选择1个或几个专家(通常一个token存在多义性,即多个领域都涉及),这样就需要为每个专家都分配非常大的容量,但是容量存储空间是静态分配的,实际中的动态计算会造成溢出或者浪费。
如果容量分配较低,如上图中的capacity_factor=1,则如果token集中在某几个专家上会使得大量token溢出(红色虚线部分);
如果容量分配较高,如上图中的capacity_factor=1.5,则有的专家会只处理少量token或者没有token处理,那么会造成存储空间的浪费;
这也是MOE模型比较难训练的一个关键因素,针对这个问题引入了负载均衡的辅助损失,这样在训练时让token在专家分布上尽可能的均匀。
论文中此部分分为两块,分别是分布式 Switch 实现和可微的负载均衡辅助损失函数
(1).分布式Switch实现
这部分主要介绍了上面图中的容量因子以及专家容量,即公式:
expert capacity = (total_tokens / num_experts)* capacity_factor
专家容量的出现是应对token在专家分布上不均匀的情况,从而保证较低(< 1%)的token溢出率。
(2).可微的负载均衡辅助损失函数
这部分是重点内容,其原因上面也提到了,首先介绍一些前置参数:
𝑁 :专家数量;
𝑖=1...𝑁 :每个专家;
𝐵 :一个批次;
𝑇 :一个批次中的token数量;
α :超参数,负载均衡辅助损失函数值控制因子,论文中使用 10−2 ;
𝑓𝑖=1𝑇∑𝑥∈𝐵1{argmax𝑝(𝑥)=𝑖} : 𝑓𝑖 是这个批次的 𝑇 个token分配到专家 𝑖 上的概率;
𝑃𝑖=1𝑇∑𝑥∈𝐵𝑝𝑖(𝑥) :其中 𝑝𝑖(𝑥) 代表token 𝑥 路由到专家 𝑖 上的概率, 𝑃𝑖 代表专家 𝑖 处理这个批次的 𝑇 个token的概率;
最终的负载损失函数:
loss=𝛼⋅𝑁⋅∑𝑖=1𝑁𝑓𝑖⋅𝑃𝑖
我们期待损失函数越小越好,则最优的情况下 𝑓𝑖 和 𝑃𝑖 都为1/N是最优的,即均匀分布时最优,其实上面的 𝑓𝑖 很好理解,即各token路由到各专家上的分布,当然均匀分布是我们最终希望达到的,理论上这一项也能满足损失函数的要求,但是 𝑓𝑖 是不可微分的,它就是一个argmax操作,无法微分就无法反向传播计算,更没办法进行梯度更新,因此引入了 𝑃𝑖 ,针对其公式中的 𝑝𝑖(𝑥) 上面计算过, 𝑝𝑖(𝑥)=𝑒ℎ(𝑥)𝑖∑𝑗𝑁𝑒ℎ(𝑥)𝑗 ,也就是专家 𝑖 的门控权重系数或者说概率,这一项是一个logits分布,理论上最大的那一项索引代表了这个token 𝑥 需要路由的专家,这里不举例子了,大家可以类比贪心采样,假如 𝑃𝑖 是贪心采样的logtis,那么 𝑓𝑖 就是对应的真实label的独热编码, 𝑃𝑖 的存在保证了损失函数的梯度更新。
论文中其他部分不再介绍了,核心部分是以上内容,其中多数是为了专家并行做的优化项,在后面的MOE架构中也进行了优化,主要了解MOE的原理及辅助损失函数的原理即可。
DeepSeek V1 (DeepSeekMoE: Towards Ultimate Expert Specialization in Mixture-of-Experts Language Models)
这篇论文是24年1月提交到arxiv上的,模型也在同月开源到huggingface上,发现一个有意思的现象,deepseek从v1到v3都没有将模型代码提pr到transformers推理框架上去,一直使用仓库中的推理代码。
首先在V1技术报告中提到了之前的MOE存在的两点问题(直接翻译):
(1)知识混杂性:现有的混合专家(MoE)实践通常采用数量有限的专家(例如 8 个或 16 个),由于token的知识是丰富多样的,将多样的知识分配给有限的专家,会导致特定专家的token很可能会涵盖多样化的知识,而使得专家变成一个杂糅多知识的专家,这样不能充分发挥专家的专业效果。
(2)知识冗余:分配给不同专家的令牌可能需要共同的知识。因此,多个专家可能会在各自参数中获取共享知识,从而导致专家参数出现冗余。这些问题共同阻碍了现有 MoE 实践中专家的专业化,使其无法达到 MoE 模型的理论上限性能。
而针对上面的问题,提出了创新性的MOE架构,主要是两个对应的策略(也直接翻译):
(1)细粒度专家划分:在保持参数数量不变的情况下,我们通过拆分前馈网络(FFN)的中间隐藏维度,将专家划分得更细。相应地,在保持计算成本不变的前提下,我们还激活更多细粒度专家,以便更灵活、自适应地组合激活的专家。细粒度专家划分能让多样的知识更精细地分解,并更精确地由不同专家学习,每个专家都能保持更高程度的专业化。此外,激活专家组合方式灵活性的提升,也有助于更准确、有针对性地获取知识。(2)共享专家分离:我们分离出特定的专家作为共享专家,这些共享专家始终处于激活状态,目的是捕捉并整合不同上下文环境中的通用知识。通过将通用知识压缩到这些共享专家中,其他路由专家之间的冗余将得到缓解。这可以提高参数效率,并确保每个路由专家通过专注于独特方面保持专业性。DeepSeekMoE 中的这些架构创新,为训练参数高效且每个专家高度专业化的混合专家(MoE)语言模型提供了契机。
V1架构示意图:
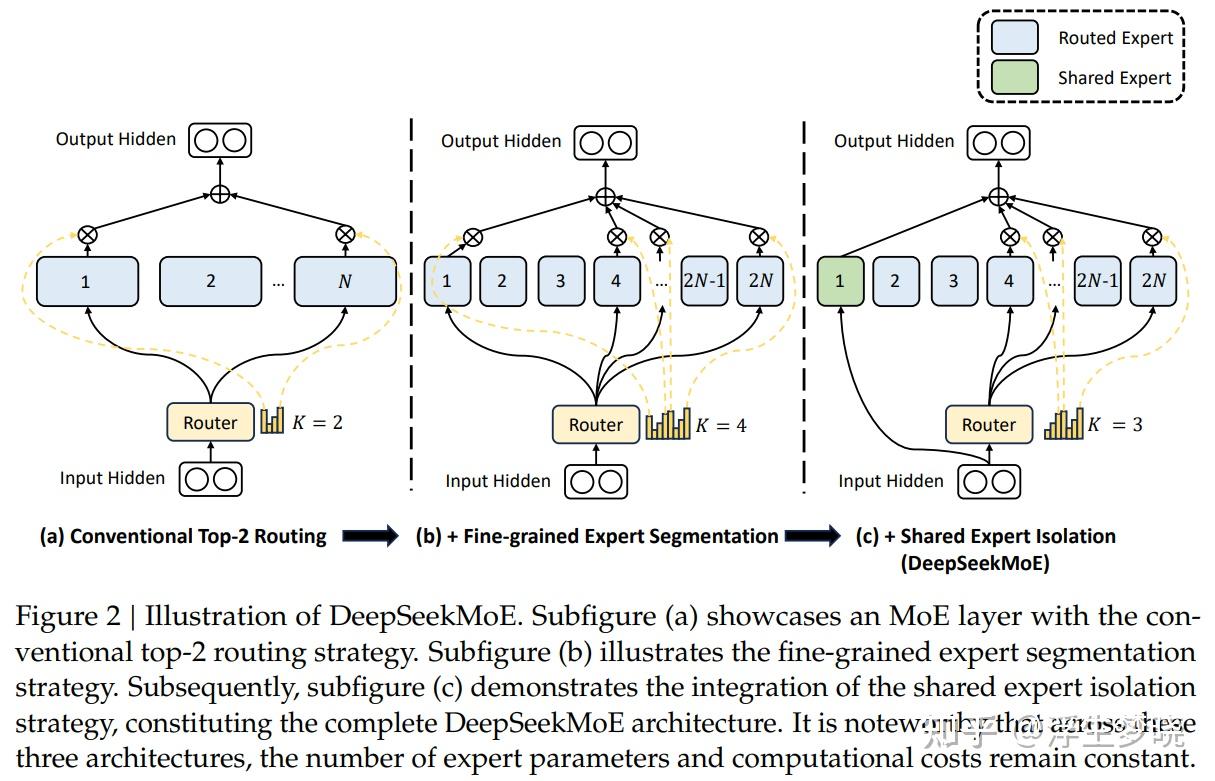
上图中(a)表示之前的MOE架构,专家分的粒度比较粗,并且没有共享专家,图(b)是将专家粒度划分的更细情况,图(c)在图(b)的基础上增加了共享专家。
V1的MOE层计算公式:
前置参数介绍:
𝐾𝑠 :共享专家的数量;
𝑚𝑁−𝐾𝑠 :路由专家的数量;
𝑢𝑡𝑙 :第 𝑙 层第 𝑡 个token的输入;
𝑒𝑖𝑙 : 𝑙 层专家 𝑖 的可学习参数,对应上篇论文的 ℎ𝑖(𝑥) ;
𝑠𝑖,𝑡=Softmax𝑖(𝑢𝑡𝑙T𝑒𝑖𝑙) :第 𝑡 个token在专家 𝑖 上的权重分值;
𝑔𝑖,𝑡={𝑠𝑖,𝑡,𝑠𝑖,𝑡∈Topk({𝑠𝑗,𝑡|𝐾𝑠+1⩽𝑗⩽𝑚𝑁},𝑚𝐾−𝐾𝑠),0,otherwise, : 选择Top-K个专家后的分值;
ℎ𝑡𝑙=∑𝑖=1𝐾𝑠FFN𝑖(𝑢𝑡𝑙)+∑𝑖=𝐾𝑠+1𝑚𝑁(𝑔𝑖,𝑡FFN𝑖(𝑢𝑡𝑙))+𝑢𝑡𝑙
可以看到最终的MOE层输出由3部分组成,分别为共享专家的输出结果,Top_K个路由专家输出结果以及残差连接。
上面公式理解上不难,延用的还是之前MOE计算思想,不再赘述了,不理解可以综合参考上篇论文中思路。
V1架构上的负载均衡
这里负载均衡优化也是为了解决(缓解)两个主要问题:(1)、负载不均衡会导致个别专家训练不充分;(2)、负载不均衡会导致专家并行时计算瓶颈。这两个问题都不难理解,上篇论文都提到了。因此,V1中负载均衡分别针对专家级别和设备级别。
1.专家级别的负载均衡损失函数
前置参数介绍:
𝛼1 :超参数,在主损失函数中控制专家级别负载均衡的因子;
𝑁′=𝑚𝑁−𝐾𝑠 :代表路由专家的数量;
𝐾′=𝑚𝑘−𝐾𝑠 :代表激活路由专家的数量;
1(⋅) :代表只是函数;
𝑇 :这个批次中的总token数量;
则:
𝑓𝑖=𝑁′𝐾′𝑇∑𝑡=1𝑇1(Token 𝑡 selects Expert 𝑖)
𝑃𝑖=1𝑇∑𝑡=1𝑇𝑠𝑖,𝑡
𝐿ExpBal=𝛼1∑𝑖=1𝑁′𝑓𝑖𝑃𝑖
其实参照上篇论文的负载均衡损失公式可以进行辅助理解,但也存在一些区别,其中 𝑓𝑖 多了一个系数 𝑁′𝐾′ ,对应到 𝐿ExpBal 中相当于乘以了一个系数 𝑁′𝐾′ ,这个系数实际上是为了消除不同激活专家数量对于损失函数的影响,使得最终的损失值在不同激活专家的情况下都能保持一个稳定的区间范围,不会浮动太大。
之所以系数 𝑁′𝐾′可以使得损失函数稳定可以通过均匀分布的计算来推理,假设有𝑇个token,每个token激活的路由专家数为 𝐾′ ,则需要分配的总token数为 𝑇𝐾′ ,将这些总token均匀的分配给 𝑁′ 个路由专家,每个路由专家需要处理的token数量为 𝑇𝐾′𝑁′ ,使用上篇论文中负载均衡损失函数可以算出𝑓𝑖=1𝑇∑𝑥∈𝐵1{argmax𝑝(𝑥)=𝑖}
也就是说 ∑𝑥∈𝐵1{argmax𝑝(𝑥)=𝑖} 代表每个专家的拼接token数量,即𝑇𝐾′𝑁′
所以 𝑓𝑖=𝐾′𝑁′
对于 𝑃𝑖=1𝑇∑𝑥∈𝐵𝑝𝑖(𝑥) 来说其值和 𝑓𝑖=1𝑇∑𝑥∈𝐵1{argmax𝑝(𝑥)=𝑖}近似,只是为了可以微分做出的选择,但有一点, 𝑃𝑖 中的 𝑝𝑖(𝑥) 是 1𝐾′ ,专家 𝑖 分到的token数量是𝑇𝐾′𝑁′,则 ∑𝑥∈𝐵𝑝𝑖(𝑥) 就等于 𝑇𝐾′𝑁′×1𝐾′ ,则最终 𝑃𝑖=1𝑁′ ,最终 𝐿ExpBal=𝛼1𝐾′𝑁′ ,这样激活专家数量就会影响最终的loss,所以在 𝑓𝑖 乘以一个 𝑁′𝐾′ 后会使得最终的 𝐿ExpBal 更加稳定。
2.设备级别的辅助损失函数
设备级别的辅助损失函数很明显就是为了专家并行方案时,token过于集中在某些卡专家而设置的。
将MOE层所有的专家进行分组,分成 𝐷 组, {𝐸1,𝐸2,…,𝐸𝐷} ,每一组放在不同的设备上,则为了平衡不同设备间负载均衡问题,损失函数为:
𝐿DevBal=𝛼2∑𝑖=1𝐷𝑓𝑖′𝑃𝑖′,𝑓𝑖′=1|𝐸𝑖|∑𝑗∈𝐸𝑖𝑓𝑗,𝑃𝑖′=∑𝑗∈𝐸𝑖𝑃𝑗,
设备级别负载均衡损失函数与专家级别负载均衡损失函数相比更加简单,不难理解,就不再赘述。
DeepSeek-V2(DeepSeek-V2: A Strong, Economical, and Efficient Mixture-of-Experts Language Model)
技术报告地址:
DeepSeek-V2技术报告中关于MOE部分是延用了DeepSeek-V1中MOE的设计模式,并相应的进行了3点优化,优化项集中在负载均衡上。
1.设备受限的路由
我们之前提到,对于MOE层在训练或推理时会采用专家并行,不同的专家的FFN分组存放在不同的GPU设备上,但是DeepSeek-V1中提到一点,其MOE专家粒度较传统MOE粒度高很多,也就是其专家数量要很多,在V2中路由专家达到160个,如果每个token选择6个激活专家,而这6个激活专家分配在不同组的设备上,就会带来很高的通信开销,所以在V2中对于每个token的激活专家所在的GPU设备数量进行了限制,限制的数量用 𝑀 表示,实验发现 𝑀≥3 个设备效果比较好,在实际中设备数量限制为3个,在被限制的设备包含的专家组中选择出6个激活专家。
2.通信负载均衡损失
在V1中负载损失包括两种,分别是专家级别以及设备级别的负载均衡损失函数,而在V2中新增了通信负载均衡损失函数。
前置参数:
𝛼3 :超参数;
𝐷 :GPU设备的数量;
𝑀 :受限制的设备数量(上一节);
𝑇 :一个批次的总token数量;
LCommBal=𝛼3∑𝑖=1𝐷𝑓𝑖′′𝑃𝑖′′,𝑓𝑖′′=𝐷𝑀𝑇∑𝑡=1𝑇1(Token 𝑡 is sent to Device 𝑖),𝑃𝑖′′=∑𝑗∈𝐸𝑖𝑃𝑗,
通信负载均衡辅助损失函数的原理与之前的类似,这里的区别之处仍是 𝑓𝑖′′ 中多了个系数 𝐷𝑀 ,增加这一项的原因与之前的专家负载均衡损失函数一致,这里不再展开推导。
这里可以思考一些上面两个优化点,设备受限的路由以及通信负载均衡损失函数都是为了针对分布式专家并行过程中的通信开销进行优化,区别在于设备受限路由保证了通信开销的上限,将所有的激活专家限制在 𝑀 个设备上。而通信负载均衡损失则保证在M设备上的每个专家尽可能的收到等量的token输入。
3.token丢弃策略
虽然上面对于负载均衡设置了很多优化方案,但实际过程中仍没办法做到有效的设备间负载均衡,意味着仍然存在有较多的token集中的少数几个设备上,本文最开始的时候提到过,负载不均衡就需要动态调整容量因子,如果容量因子大于1则专家是可以有buffer来存储一定的token,而如果容量因子为1,则意味着每个设备的专家没有存储计算能力以外token的buffer,这样就会造成这个token溢出,也就是在本层的MOE不再参与专家计算,直接残差链接到下一层。考虑到更加高效的MOE层计算,因此实际中必须会存在token溢出的情况,而如何选择哪些token来丢弃需要一定策略,实际策略也比较简单,每个token分发到对应的专家上都会有个分值,直接对分值进行降序排列,超过这个专家容量的token进行丢弃。一定注意这里的丢弃只是在本层MOE中这个专家不再计算此token的hidden state,不影响下一层。
以上三点是DeepSeek-V2中关于MOE的主要优化点,可以看到仍集中在负载均衡上的优化,说白了是为了高效,这一点与V3相对应,可以看出这个团队一直在追求的方向。
DeepSeek V3(DeepSeek-V3 Technical Report)
技术报告:
V3相较于V2在MOE侧也存在了几个优化。
1.MOE层计算的变化
下面是V3的MOE层计算公式:
ℎ𝑡′=𝑢𝑡+∑𝑖=1𝑁𝑠FFN𝑖(𝑠)(𝑢𝑡)+∑𝑖=1𝑁𝑟g𝑖,𝑡FFN𝑖(𝑟)(𝑢𝑡),𝑔𝑖,𝑡=𝑔𝑖,𝑡′∑𝑗=1𝑁𝑟𝑔𝑗,𝑡′,𝑔𝑖,𝑡′={𝑠𝑖,𝑡,𝑠𝑖,𝑡∈Topk({𝑠𝑗,𝑡|1⩽𝑗⩽𝑁𝑟},𝐾𝑟),0,otherwise,𝑠𝑖,𝑡=Sigmoid(𝑢𝑡𝑇𝑒𝑖),
这里是V1,V2中MOE层的计算公式:
ℎ𝑡𝑙=∑𝑖=1𝐾𝑠FFN𝑖(𝑢𝑡𝑙)+∑𝑖=𝐾𝑠+1𝑚𝑁(𝑔𝑖,𝑡 FFN𝑖(𝑢𝑡𝑙))+𝑢𝑡𝑙,𝑔𝑖,𝑡={𝑠𝑖,𝑡,𝑠𝑖,𝑡∈Topk({𝑠𝑗,𝑡|𝐾𝑠+1⩽𝑗⩽𝑚𝑁},𝑚𝐾−𝐾𝑠),0,otherwise,𝑠𝑖,𝑡=Softmax𝑖(𝑢𝑡𝑙𝑇𝑒𝑖𝑙).
公式中每个字符含义不再重复介绍了,大家可以往前面翻看一下,可以很明显的看到在V3中 𝑠𝑖,𝑡 的计算方式发生了变化,也就是门控函数发生了变化,从SoftMax优化为了Sigmoid,至于为什么要这么做,论文中并未提及,以下是个人的一些猜测,不保证正确。
首先V3的模型远大于V2,V3的每层MOE中有256个路由专家,8个激活专家。但V2中只有160个路由专家,6个激活专家,从参数上就可以发现V3的门控函数计算量远大于V2,大家也都清楚当计算维度变大时SoftMax的前向和反向是很耗费计算资源的,而Sigmod直接将数值映射到[0,1]之间,相对来说更加简单。可能实现效果也类似,因此为了更加高效的训练从而进行了替换。
2.无辅助损失的负载均衡
从V1到V2可以发现DeepSeek使用了多个辅助的负载均衡损失来降低通信开销并提升训练的稳定性,包括专家级别、设备级别、通信级别,但是这些负载均衡损失加到主损失函数后势必会影响主损失函数的训练效果,从而影响模型的最终训练效果。但没有辅助的负载均衡损失又会造成通信开销可训练的不稳定,在这里V3提出了一种新的平衡策略,丢弃到之前所有的辅助负载均衡损失,在每个专家计算时增加一个偏置项 𝑏𝑖 ,将这个偏置项添加到上面V3的MOE层计算公式中 𝑠𝑖,𝑡 后面,也就是专家对于token亲和值权重上:
𝑔𝑖,𝑡′={𝑠𝑖,𝑡,𝑠𝑖,𝑡+𝑏𝑖∈Topk({𝑠𝑗,𝑡+𝑏𝑗|1⩽𝑗⩽𝑁𝑟},𝐾𝑟),0,otherwise.
这里的偏置项 𝑏𝑖 是一个可学习的参数值,每个专家都有一个对应的偏置项,这个值只用于对路由选择本专家进行控制,并不参与其他运算。
另外训练中还有一个超参数 𝛾 ,当对应的专家负载过高时,会让这些专家的偏置项减去𝛾,这样路由到这些专家的token会减少,当有的专家负载过低时,会让这些专家的偏置项加上𝛾,从而增加token路由到这些专家的概率。
通过实验发现,通过这种方法比之前复杂的多种辅助负载均衡损失训练过程中负载均衡的效果更优。
3.互补序列层面的辅助损失
这个标题名字是直接翻译的,读起来不知道在说什么,实际上是因为之前丢弃了所有的辅助负载均衡损失,使用一个偏置项来平衡负载效果虽然好,但为了防止任何单个序列内出现极端不平衡的情况,从而采用的一种辅助损失函数的方法,这个辅助损失只针对一个样本或者说一个序列中的token。
序列级别辅助负载均衡损失函数:
𝐿Bal=𝛼∑𝑖=1𝑁𝑟𝑓𝑖𝑃𝑖,𝑓𝑖=𝑁𝑟𝐾𝑟𝑇∑𝑡=1𝑇1(𝑠𝑖,𝑡∈Topk({𝑠𝑗,𝑡|1⩽𝑗⩽𝑁𝑟},𝐾𝑟)),𝑠𝑖,𝑡′=𝑠𝑖,𝑡∑𝑗=1𝑁𝑟𝑠𝑗,𝑡,P𝑖=1𝑇∑𝑡=1𝑇𝑠𝑖,𝑡′,
这里序列级别辅助均衡均衡损失中的 𝑇 与上面V1中专家级别的辅助损失均衡中的 𝑇 不同,这里指的是一个样本序列,而V1中的专家级别则是一个batch中的所有token,两者粒度上不同,这里粒度更细一些。
4.设备受限的路由
这一点是沿用了V2中的设备受限路由,最多选择 𝑀 个设备中的专家进行路由,通过这个策略可以做到通信与计算的重叠。
5.不再使用token丢弃策略
在V2中虽然使用了多种辅助的负载均衡损失函数,但实际训练中都没有达到很好的负载均衡,而在V3中训练中通过引入偏置项来控制路由的策略,以及序列级别的token辅助负载均衡损失有效的使得整个训练过程负载均衡,从而不再寻token丢弃的策略。
OK,以上是4篇论文中关于MOE部分的笔记整和,内容上比较庞杂,希望串联起来可以对读者理解MOE有一个比较完整的脉络,顾拜!!!
posted on 2025-02-20 11:44 ExplorerMan 阅读(1252) 评论(0) 收藏 举报




 浙公网安备 33010602011771号
浙公网安备 33010602011771号