堆排序
堆排序是采用树的形式的数据结构来进行排序的，其中每一个堆都是完全二叉树。堆排序分为大根堆与小根堆，大根堆（小根堆）表示在完全二叉树中，所用的非叶子节点都大于等于（小于等于）他们左右子节点（存在）。所以堆的顶点不是最大数就是最小数。这样的话我们就可以借助这种性质，每次都取出大根堆（小根堆）的顶点数，形成有序序列。
基本步骤
首先要明白堆在数组中的表示方式。是按照从堆得顶点开始从上往下，从左往右存放到数组中。
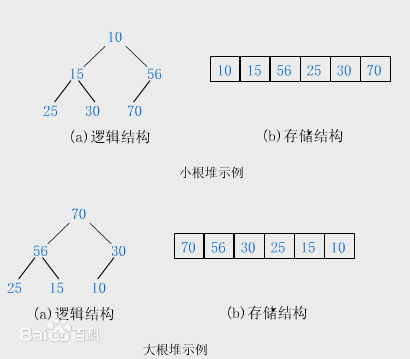
通过上面的图应该很容易理解堆在数组中的存放位置
设数组为a[0...n-1]
我们会发现非叶子节点的i的左右子节点(存在)在数组中的位置分别为i*2+1、i*2+2。而在数组中最后一个非叶子节点的位置可以表示为n/2-1(n为数组的大小)。借助这些我们可以实现小根堆与大根堆的形成，同时也能实现堆排序。
- 首先生成小根堆或大根堆，这里以小根堆为例。我们可以将每一个非叶子节点都看做是一个最小的完全二叉树，将他们都生成小根堆，从最后一个非叶子节点开始，把其当做是根节点，逐步向前进行创建小根堆。例如上图中的大根堆，将其变成小根堆的步骤，先以
30为根节点，根据小根堆的性质，需要与10互换位置;再以60为根节点，发现需要与15互换位置；最后与70为根节点，需要与原来30的位置即现在交换位置的10互换位置，最终形成小根堆。 - 然后就是取出形成的小根堆得顶点值，将其与堆中第
N(N=n)个节点互换位置，即a[N-1]。 - 此时小根堆被破坏，再重新生产小根堆
N--，但此时要生成的数的范围为a[0...N-1]。 - 重复上面的步骤
2、3，直到N=1，即a[0]，排序结束。
实现
不管是最开始的创建小根堆还是每次取了顶点数之后再调整成小跟堆，他们的逻辑都是一样的，即都是与其关键字的子节点进行比较选出最小值，将其放到父节点处的位置。所以调整小根堆的代码如下：
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
/**
* 调整成最小堆
* @param arr 数组
* @param top 堆顶位置
* @param tail 堆未位置
*/
public static void fitToMinHeap(int[] arr, int top, int tail) {
int i = top;
int temp = arr[i];
int j = 2 * i + 1;//找到子节点
while (j < tail) {
if (j + 1 < tail && arr[j + 1] < arr[j])//找出左右子节点中的最小
j++;
if (arr[j] >= temp)//子节点都大于父节点则跳出
break;
arr[i] = arr[j];//将子节点向上移,即移到父节点
i = j;
j = 2 * i + 1;
}
arr[i] = temp;
}
|
这里的位置交换没有直接每次都进行交换，而是与前面的快速排序一样，最后才将关键字放到他所要存放的位置。
主要的生成最小堆的方法实现了，下面就是取数，再调整，再取数的循环实现。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
public static void heapSort(int[] arr) {
int n = arr.length;
for (int j = n / 2 - 1; j >= 0; j--)//从最后一个非叶子节点开始,初始化生成数组表示的最小堆
fitToMinHeap(arr, j, n);
for (int i = n - 1; i > 0; i--) {//每次拿出堆的顶点值
//把堆中的顶点与a[i]点互换
int temp = arr[0];
arr[0] = arr[i];
arr[i] = temp;
fitToMinHeap(arr, 0, i);//交换后再对前i个节点进行最小堆化
}
}
|
当然使用小根堆进行排序后的结果是逆序序列，即从大到小的排序
总结
个人认为，堆排序要理解以下几点
- 何为小根堆、大根堆
- 堆的创建原理
- 堆排序的取数原理
通过以上几点的理解就能很好的掌握堆排序。最后堆排序为不稳定排序，且时间复杂度为O(nlogn)。
转载请指明出处 idisfkj博客：https://idisfkj.github.io
