Trie树-字典树

字典树

Trie树的本质，就是利用字符串之间的公共前缀，把重复的前缀合并在一起。
（图片来自于比《数据结构与算法之美》）

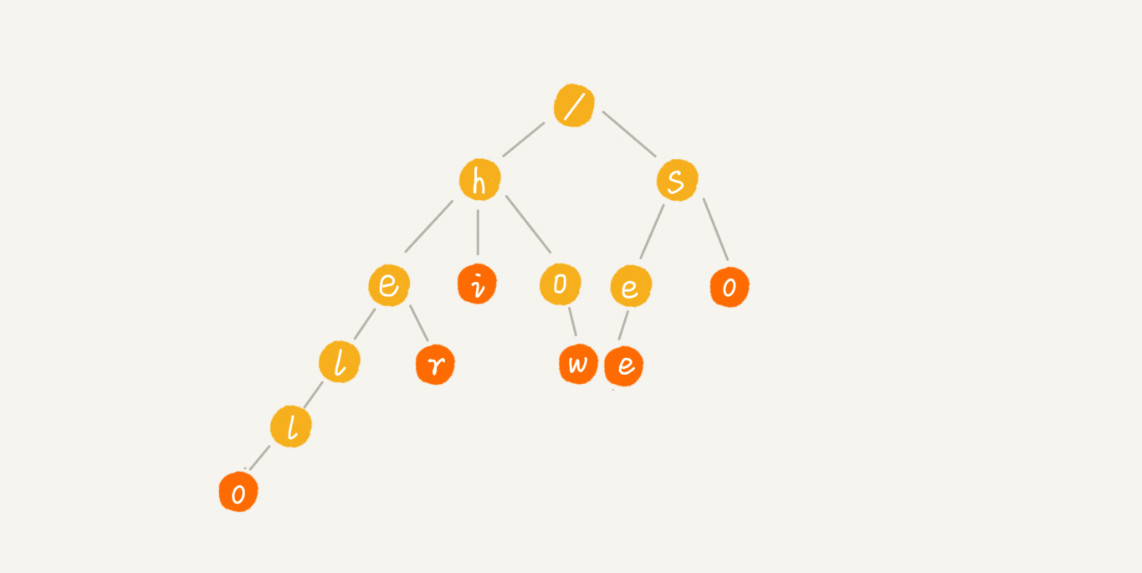
根节点不包含任何信息，每个节点表示一个字符串中的字符，从根节点到红色节点（并不一定都是叶子节点，红色节点表示到此为止是一个字符）的一条路径表示为字符串

代码实现

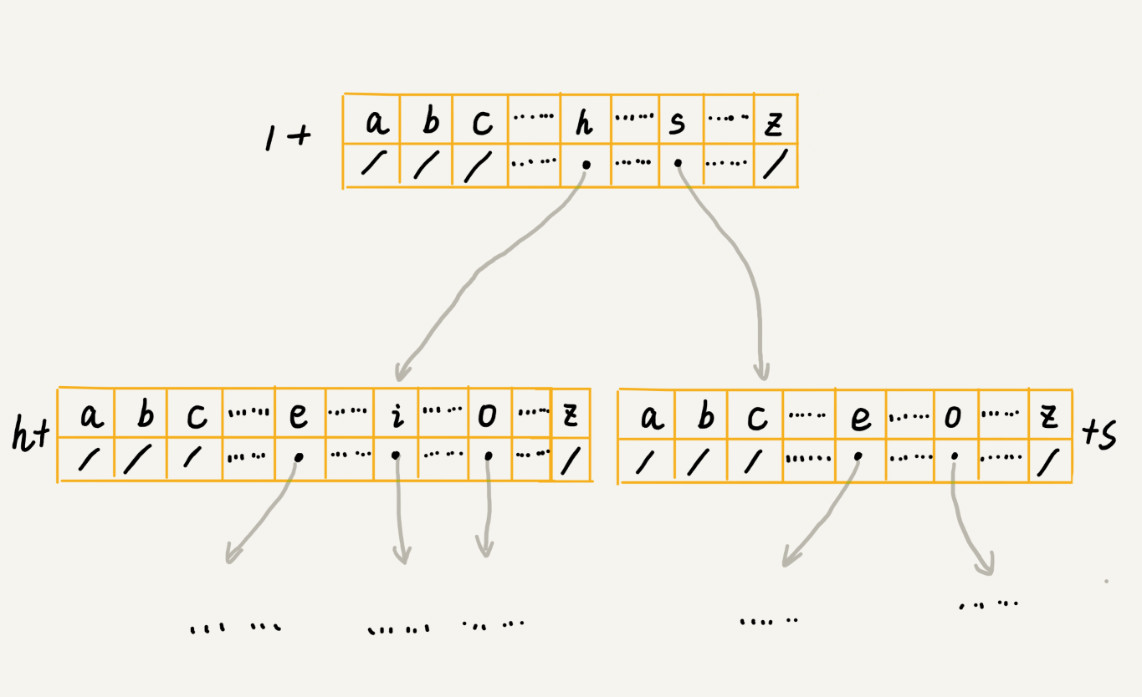
1. 经典存储方式--散列表

下标0-25存储 a-z的指针，字符子节点不存在，下标位置存储null。

class TrieNode {
  char data;
  TrieNode children[26];
}

java代码

例题

电话号码归属地，字典序解法

public class Trie {
  private TrieNode root = new TrieNode('/'); // 存储无意义字符

  // 往Trie树中插入一个字符串
  public void insert(char[] text) {
    TrieNode p = root;
    for (int i = 0; i < text.length; ++i) {
      int index = text[i] - 'a';
      if (p.children[index] == null) {
        TrieNode newNode = new TrieNode(text[i]);
        p.children[index] = newNode;
      }
      p = p.children[index];
    }
    p.isEndingChar = true;
  }

  // 在Trie树中查找一个字符串
  public boolean find(char[] pattern) {
    TrieNode p = root;
    for (int i = 0; i < pattern.length; ++i) {
      int index = pattern[i] - 'a';
      if (p.children[index] == null) {
        return false; // 不存在pattern
      }
      p = p.children[index];
    }
    if (p.isEndingChar == false) return false; // 不能完全匹配，只是前缀
    else return true; // 找到pattern
  }

  public class TrieNode {
    public char data;
    public TrieNode[] children = new TrieNode[26];
    public boolean isEndingChar = false;
    public TrieNode(char data) {
      this.data = data;
    }
  }
}

构建Trie树的过程需要扫描所有的字符串，时间复杂度是O(n)，一旦构建成功，后续的查询操作会非常高效。
Trie树有可能会很浪费内存，但确实非常高效。

//Trie树的例题。

来源于这个博主的代码：https://blog.csdn.net/u011721440/article/details/81559189

#include <iostream>
#include <string>
using namespace std;
#define N 20010
#define M 10 //child :0-9;
struct Trie
{
	string s; //一般是空的，如果到了节点字符，就写地名。
	int next; //去下一个节点，被使用的k，如果没有，则是-1，表示这个点没有用到。（插入）
}rt[N][M];


int cnt; //point to index which just used （被用到的k，做标记位置）
void Trie_clear(int k)
{
	for (int i = 0; i < M; ++i)
	{
		rt[k][i].next = -1;
		rt[k][i].s.clear();
	}
}

void Insert(string& s1, string& s2)
{
	int k = 0; // point to root node
	for (int i = 0; i < s1.length(); ++i)
	{
		int id = s1[i] - '0';
		if (rt[k][id].next == -1)
		{
			rt[k][id].next = ++cnt;
			Trie_clear(cnt);
		}
		if (s1[i + 1] == 'x')
		{
			rt[k][id].s = s2;
			break;
		}
		k = rt[k][id].next;
		
	}
}

string find_val(string& s1)
{
	int k = 0; //point to root node
	for (int i = 0; i < s1.length(); ++i)
	{
		int id = s1[i] - '0';
		if (rt[k][id].next == -1)
			return "";
		if (rt[k][id].s != "")
		{
			return rt[k][id].s;
		}
		k = rt[k][id].next;
	}
	return "";
}

int main()
{
	int T, n, m;
	cin >> T;
	while (T--)
	{
		cin >> n;
		string s1, s2;
		cnt = 0;
		Trie_clear(cnt);
		for (int i = 0; i < n; ++i)
		{
			cin >> s1 >> s2;
			s1 += 'x'; //害怕输入数据没有x
			Insert(s1, s2);
		}
		cin >> m;
		while (m--)
		{
			cin >> s1;
			s1 += 'x';
			string ans = find_val(s1);
			if (ans == "") cout << "unknown" << endl;
			else cout << ans << endl;
		}

	}
	return 0;
}