买苹果

题目描述如图：

提示：

有两种带子，分别只能装6个和8个，不能多装，也不能少装。求最小的需要的袋子数。

思路：

显然如果能用8个袋子装绝对不用6的袋子，8的袋子能装更多，所需要的袋子数越少。

所以，我们先看看这n个苹果能不能用8的袋子装，如果不行，我们看看剩下的可不可以用6的袋子装。

此时有两种情况，1，剩下的苹果正好可以被用6的袋子装完，那就直接返回结果；2，剩下的苹果还是装不下。这时候，我减少一个8的袋子，那么剩下的苹果数就会在原来的基础上多出8个，这是我再来看剩下的苹果数能不能用6的袋子装完，以此类推。。。如果一直不行，就返回-1了。

代码：

private static int minBase6(int num) {
    return ((num%6) == 0 ? num/6 : -1);
}

//普通法
public static int minBags(int num) {
    if (num < 0 || num % 2 == 1) {
        return -1;
    }
    int bag6 = -1;
    int bag8 = num / 8;
    int rest = num - 8*bag8;
    while (bag8>=0 && rest<24) {
        int temp = minBase6(rest);
        if (temp != -1) {
            bag6 = temp;
            break;
        }
        rest = num - 8*(--bag8);
    }
    return bag6 == -1 ? -1 : (bag6+bag8);
}

先给6的袋子数量初始化为-1（这很有用）。剩下的逻辑都是之前讲过的，。唯一可能需要注意的地方是，为何while循环中还多了一个rest<24的条件呢？这是因为，当剩下的苹果数越来越多以至于都超过了24的时候，不用继续下去了，肯定再怎么装都装不了。这是因为24是6和8的最小公倍数。

举个例子，现在我想买的苹果数是45个。我们根据代码逻辑一步步来还原：

45能否全部用8的袋子来装？45/8=5余5，还剩5个，也不能用6的来装，这时减少一个8的袋子，于是剩下苹果13个；

13个苹果能否用6的来装？不行，再减少一个8的袋子，于是现在剩下苹果21个；

21个苹果能否用6的来装？不行，再减少一个8的袋子，于是现在剩下苹果29个；

29个苹果，超过24了。你要判断29能不能用这两种袋子装完，肯定要先判断它能不能被8的装完；

29/8=3余5，你会发现5能不能被6的装完这种情况你已经做过判断了，而且判断结果是不行。

为什么说bag6初始化为0有大作用呢，这是因为只要剩余苹果树一直无法用6的袋子装完，while循环中的if语句就一直进不去，那么bag6就不会被赋新的值，它就会一直保持-1的初始值。

等到最后返回结果的时候，判断一下bag6是不是-1就可以了。

——————————————————————————————————————

接下来介绍另一种方法，也称打表法。

如果按照上面的代码去实现，然后将n的取值从1一直往下取，并分别打印出来，你会发现一个有趣的规律：

如果n是负数，那么最后结果一定是-1；

如果n是偶数，当它超过18时，它（偶数）一定是每4次变化一次，每次变化都是在原来的基础上加1：

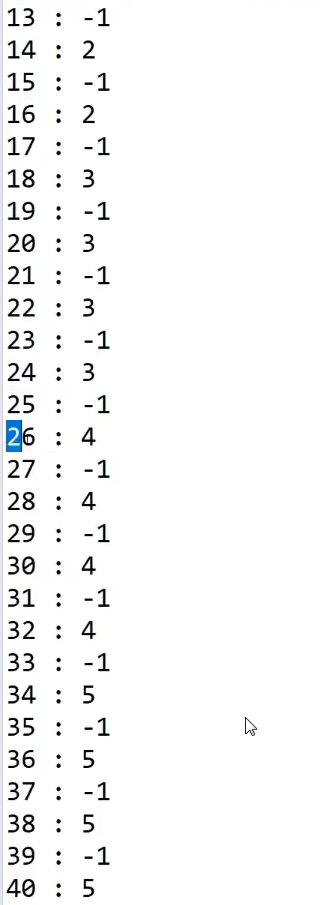
你不妨自己打印一下去试试。

所以，我们不用搞清楚它内部的逻辑，只需要根据规律总结出数学结论就可以了。代码如下：

//打表法
public static int awesomeMinBags(int num) {
    if ((num & 1) != 0) {  //是奇数，就返回
        return -1;
    }
    if (num < 18) {
        return num == 0 ? 0 : (num == 6 || num == 8) ? 1 : (num == 12 || num == 14 || num == 16) ? 2 : -1;
    }
    return (num - 18) / 8 + 3;
}

 这种方法的输出结果一定和上面那一种是一样的。

现在，我们再来看一道类似的题：

有两头牛吃n份青草，怎么个吃法呢？两头牛规定了先手和后手，先手先吃，然后后手吃，然后先手再吃，接着后手再吃，以此类推。不管是先手还是后手，每次只能吃4的n次方份青草，即他们一次只能吃0,1,2,4,16,64，...份青草，最终谁先吃完这n份青草，谁获胜。

思路

我们先想想常规方法怎么做。我们可以先吃1份，看情况，没输的话，下次就吃2份，还没熟的话，下次就吃4份，以此类推。所以我们可以用递归的方法来做。

代码如下：

public static String winner(int n) {
    if (n < 5) {
        return (n == 0 || n == 2) ? "后手" : "先手";
    }
    int base = 1;
    while (base <= n) {
        if (winner(n - base).equals("后手")) {
            return "先手";
        }
        if (base > n/4) {
            break;
        }
        base *= 4;
    }
    return "后手";
}

若不看while循环中的两个if，base每次乘4就是所说的每次的去试的方法。但是要防止越界啊，base每次乘4这是指数级增长，很容易超出int存储范围的，因此，我要判断一个现在的base和n/4哪个大。一旦base更大，那么它乘以4之后一定会超出n。这种写法最保险，若不这么写，你base已经越界了，还判断有什么用呢？一样会报错的。

至于第一个if，这就是递归的核心，n-base就是给后手吃的草。那后手怎么吃？同时考虑，如何去递归？那我假设先手跟自己博弈，先手吃完后，立刻开始跟自己博弈的比赛，那么这场比赛中的先手就是实际比赛中的后手，而先手跟自己博弈比赛中的后手，其实就是实际比赛中的先手，也就是自己。

所以，若这个winner递归调用后返回的结果是后手，其实也就是自己赢了，返回先手；

若一直不返回，还被break掉了，那显然先手不可能赢了，于是返回后手。

现在打印看看规律，你会发现基本上每五次的结果都是一样的，即“先后先先后”。

所以，判断n能不能被5整除，以及被5除后余数是不是2，若满足，返回后手；否则返回先手。