树链剖分
树链剖分贼难,本蒟蒻看了好几篇博客才勉强弄懂一丢丢,现在写篇博客,记录一下自己学习树链剖分并观摩大佬代码的时候遇到的一些问题以及解决办法还有对代码的理解。
(当然也不能这么说自己对不对,至今仍对在学校上篮球课时某兄弟说过的一句话印象深刻:首先排除自己菜)
首先是树链剖分的一些概念,包括重链轻链重儿子轻儿子这些,我就不一一阐述了,因为很忙,没时间写。推荐一篇博客吧:
https://www.cnblogs.com/ivanovcraft/p/9019090.html
我们直接从代码入手:
1.添加边:
这部分代码是这么写的:
1 //向图中添加一条边 2 void add(int x, int y) 3 { 4 e[++cnt].next = head[x]; //这条边的下一条边 5 e[cnt].to = y; 6 head[x] = cnt; 7 }
这种写法初学者说实话很难看懂,本蒟蒻看了好久才明白,现在详细说说我是怎么理解的:
这种添加边的方式与dfs是密切相关的,为更好地理解这个代码,我们结合dfs来看一下,以下面这个图为例:
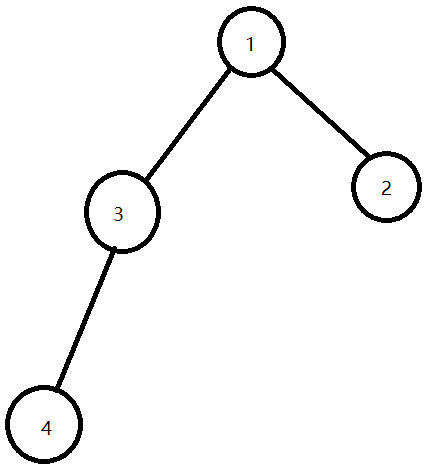
我们添加边的顺序是:1-2;1-3;3-4.
在这之前,我们需要在前面声明一些变量:
1 int cnt = 0, cut = 0; 2 const int maxn = 1e5 + 10; 3 struct edge { 4 int next, to; 5 }; 6 edge e[maxn << 1]; 7 int head[N], deep[N], sizes[N], father[N], son[N], rk[N], top[N], id[N];
我们先只看cnt,e数组,head数组,其他都不管
好,我这样声明以后,head数组里面现在全是0,e数组的next,to也全是0,这是前提。
然后我添加第一条边:1-2.那么,x=1,y=2.所以e[1].next=0.这意味着,第1条边的下一条边目前的标号是0。这很好理解,因为现在还只有一条边嘛,那我唯一的这条边的下一条边的编号肯定是0啊;然后,e[1].to=2.这表示,第1条边指向的节点标号是第2号节点;最后,head[1]=1.这表示啥意思呢?我也不知道,不过没多大影响,我们先继续往后看。
现在我们开始添加第2条边:1-3.那么,x=1,y=3.则,e[2].next=head[1]=1;e[2].to=3;head[1]=2.这里我先不写理解,我们接着往下看:
现在是第3条边:3-4.所以,x=3,y=4.那么,e[3].next=head[3]=0;e[3].to=4;head[3]=3.好,看到这里,如果你也像我一样之前从没接触过这些东西的话,那你肯定已经开始看不懂了,没关系,我们先记下这些值。
现在我们来跑一遍dfs.
dfs代码是这样的:
1 void dfs1(int x) 2 { 3 sizes[x] = 1; 4 deep[x] = deep[father[x]] + 1; 5 for (int i = head[x]; i != 0; i = e[i].next) { 6 int v = e[i].to; 7 if (v != father[x]) { 8 father[v] = x; 9 dfs1(v); 10 //回溯更新 11 sizes[x] += sizes[v]; 12 if (sizes[son[x]] < sizes[v]) { 13 //son[x]一定有一个值,是啥我不管,但我只要发现这个值的size比v的size小,我就立刻更新son[x] 14 //选取size更多的那个成为重儿子 15 son[x] = v; 16 } 17 } 18 } 19 }
我写的那两行注释涉及到后面的东西,现在先不管。
好,我现在以1为起点开始dfs.那么,i=head[1]=2.那么,v=e[2].to=3.注意这里是第2条边指向的节点。为了防止产生疑惑,把边的序号标上:
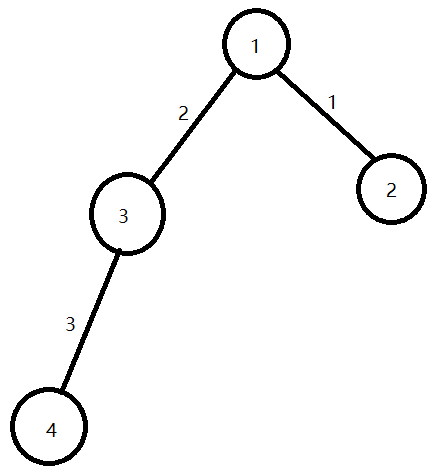
那么现在v就等于3了,所以我就开始dfs(3).
现在,x=3.所以i=head[3]=3.v=e[3].to=4.所以开始dfs(4).
x=4,i=head[4]=0.诶,这个时候你就会发现,到头了,那么根据递归函数的性质,我就开始回退。而且你有没有发现,到目前为止访问节点的顺序正好就是深度优先的顺序!
今天先睡觉了。


