树状数组及其应用

树状数组是一种比较高级的数据结构，大概是这样子的：

 

啥意思呢？别慌。先看最下面那一排，A数组表示原数组，就是我们最开始创建的数组，里面保存的是原始数据。而上面的C数组就是树状数组了。我们可以看到，C数组里面，有些有叶子节点，有些没有。比如说，在这棵树中，C[1]就是一个叶子节点，而C[2]不是，并且它有两个叶子节点，C[4]则有4个，以此类推。

那么C数组里面的值是怎么确定的呢？我们再看上面那张图：C[1]就在A[1]的上面，因此它俩的值相等。再看C[2]，它有两个叶子节点，那么根据这种关系，我们可以推断它的值是A[1]和A[2]的和。C[3]呢，在A[3]的上面，那么C[3]=A[3].再看C[4]，一共有四个叶子节点，因此，它的值是A[1]到A[4]这四个数的和。因此，C数组，也就是树状数组，维护的是某一段区间的和。

那我怎么判断C数组中哪些是叶子节点哪些又不是呢？

这里直接拿我们上课的PPT过来解释了[狗头保命]

我们把1到8这八个数字先全部转换为二进制形式：

 

 我们观察一波这些二进制数最右边1的位置，再对应图一看，就可以得到如下结论：

 

 所以：

 

 所以说，其实树状数组维护的是区间和。

好啦，现在知道C数组是啥东西了，我们来看看怎么写一套C数组的模板：

在这之前，我们先写一个lowbit函数：

int lowbit(int x)
{
    return (x & (-x));
}

这是啥意思，又有啥用呢？别急，听我慢慢分析。

上面的截图中我们看到了需要计算2的x次幂，那这个编程怎么实现？莫非我还要写一个专门用于作幂运算的函数？非也非也，进入二进制的世界，我们其实可以很容易地解决这个问题。

 

就是这样，看不懂没关系，直接用就对了（其实是老师上课讲过，但我没做笔记，现在忘了QAQ）

 

看到这里，你可能忘记这个x表示什么意思了，没关系，这里再强调一下:x表示的是这个数在对应二进制的形式下，从右到左连续的0的个数。

 

那这个2的x次幂，我们直接用lowbit函数实现。

 

再看：

 

对于原数组的求和，我们现在就可以用树状数组来实现：

 

 

 既然C数组已经是某一段区间的和了，那么，对原数组整体求和的话，完全可以通过求C数组的和来简化，具体的计算公式就像上面那样。

现在，再来看看怎么更新树状数组：

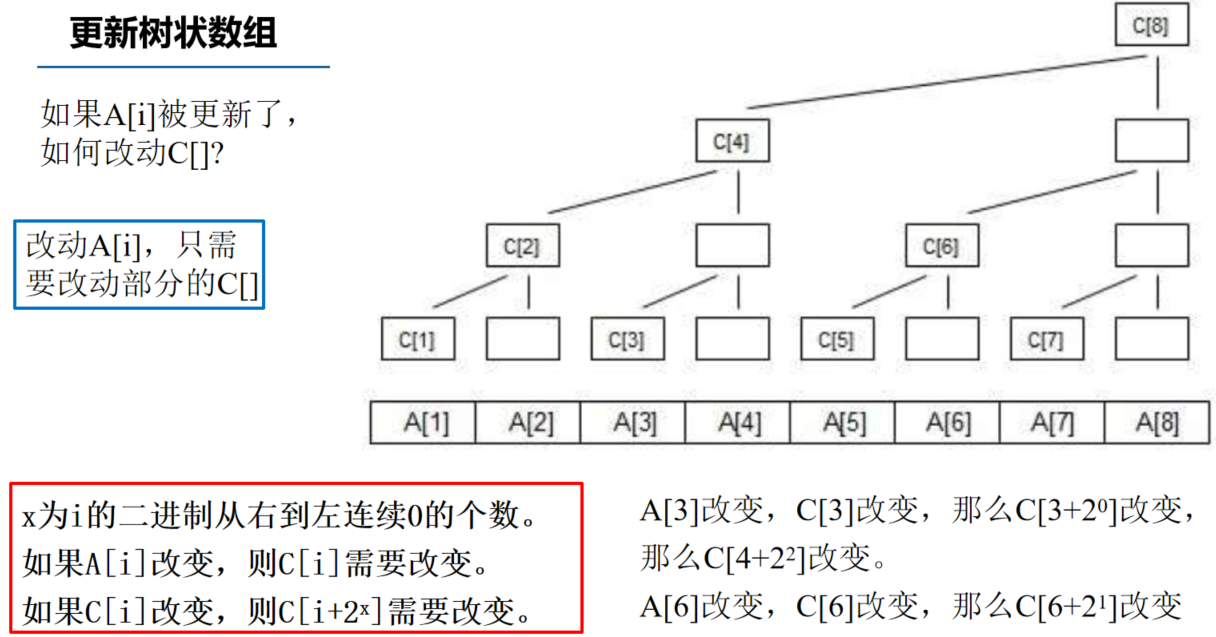
See?其实更新的话也不需要改很多。那咋改呢？

 

 

这样改就行了。

 

写到这，相信你已经能够独立地写出创建一个树状数组然后实现求和和更新操作了。不过这里我还是把我的代码贴出来，代码中还包括了一些测试函数，经过本人测试是没有问题的（当然测试数据还不够多，也可能有问题，欢迎指正！）

 

 

#include <iostream>
#include <algorithm>
#define N 100
using namespace std;
int A[N], C[N];
int n;

int lowbit(int x)
{
    return (x & (-x));
}

//建立树状数组
void buildC(int a[], int c[])
{
    for (int i = 1; i <= n; ++i) {
        int j = i - lowbit(i) + 1;
        while (j <= i) {
            c[i] += a[j];
            j++;
        }
    }
}

//求的是A数组的前i个值的和
int getSum(int i)
{
    int sum = 0;
    while (i > 0) {
        sum += C[i];
        i -= lowbit(i);
    }
    return sum;
}

//更新树状数组
void update(int i, int value)
{
    while (i <= n) {
        C[i] += value;
        i += lowbit(i);
    }
}

void showSum()
{
    int i, sum;
    cout << "输入求和的下标值:";
    cin >> i;
    sum = getSum(i);
    cout << "和为:" << sum << endl;
}

void show(int x[])
{
    for (int i = 1; i <= n; ++i) {
        cout << x[i] << " ";
    }
    cout << endl;
}

int main()
{
    cout << "输入数组长度:";
    cin >> n;
    cout << "输入A数组的值:" << endl;
    for (int i = 1; i <= n; ++i) {
        cin >> A[i];
    }
    buildC(A, C);
    show(C);
    showSum();
    return 0;
}

 

现在，我们来看看一道题（所谓应用当然就是做题啦）：

求一个数组中的逆序对个数：

所以什么是逆序对？

在一个排列中，如果一对数的前后位置与大小顺序相反，即前面的数大于后面的数，那么它们就称为一个逆序。一个排列中逆序数的总数就是这个排列的逆序数。

好了，这个题也可以用暴力，不过这样时间成本太高了，显然也不符合这篇博客的精神！

我们就用树状数组来写！

大概思路就是这样的：

 

 

我们再来看看一系列图的演示：

 

 

 

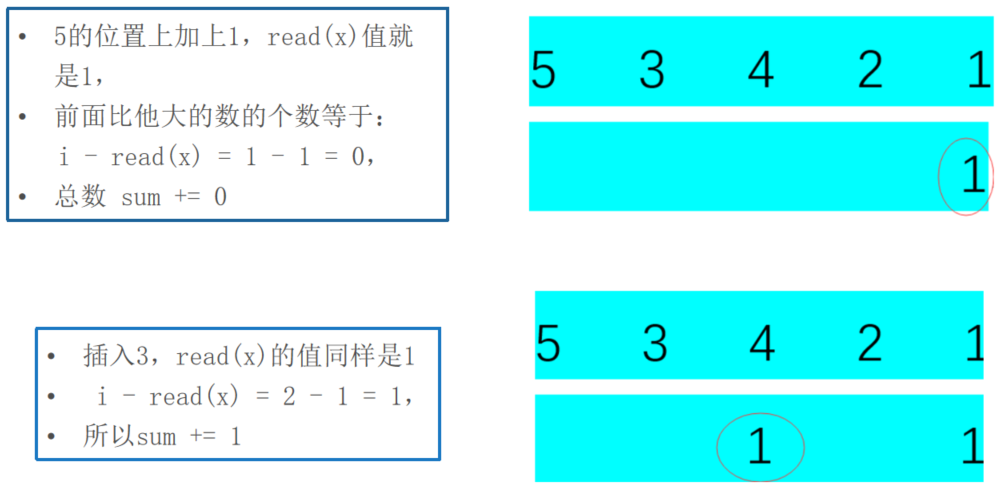
这样子其实很明白了

现在来看看代码：

#include <iostream>
#define N 100
using namespace std;
int C[N];
int n, d, res = 0;

int lowbit(int x)
{
    return (x & (-x));
}

//更新树状数组
void insert(int i, int value)
{
    while (i <= n) {
        C[i] += value;
        i += lowbit(i);
    }
}

//读取数组的前i个和
int read(int i)
{
    int sum = 0;
    while (i > 0) {
        sum += C[i];
        i -= lowbit(i);
    }
    return sum;
}

int main()
{
    cin >> n;
    memset(C, 0, sizeof(C));
    for (int i = 1; i <= n; ++i) {
        cin >> d;
        insert(d, 1);
        res += (i - read(d));
    }
    cout << res << endl;
    return 0;
}

一开始，我是对于原数组数据全部读入后，再根据这个数组创建一个树状数组。然后按照上面的思路求和。但是后来发行不行，运行出来的结果不对。其实这样做有一个问题：如果我一次性把数据全部读入，那么用一个for循环遍历，这样就相当于，每遍历到一个数据，就需要建立一个树状数组，然后再求和。这样显然花费时间很多。

所以这里我们换一种思路。我们实现建立一个数组，这个数组里面的所有数据都初始化为0.这个数组当成树状数组。我们每读入一个数据，就更新一下这个数组。然后再求和。那么这样一来，就很容易了。

 

 

 由于OJ进不去，这份代码应该还AC不了，不过稍微改一下就行了，等我能进OJ了再来改吧。