图

现在我们分别创建图的结点、边和图本身的类：

Node.java:

package com.hw.Graph;

import java.util.ArrayList;

public class Node {
    public int value;
    public int in; //入度
    public int out; //出度
    public ArrayList<Node> nexts; //从该结点可以通向的结点
    public ArrayList<Edge> edges; //与该结点相连的所有边

    public Node(int value) {
        this.value = value;
        in = 0;
        out = 0;
        nexts = new ArrayList<>();
        edges = new ArrayList<>();
    }
    
    public String toString() {
        return value + "";
    }
}

Edge.java:

 

package com.hw.Graph;

public class Edge {
    public int weight; //权重
    public Node from; //始结点
    public Node to; //末结点
    
    public Edge(Node from, Node to, int weight) {
        this.from = from;
        this.to = to;
        this.weight = weight;
    }
    
    public String toString() {
        return "边:<" + from + "," + to + ">,权值:" + weight;
    }
    
}

 

Graph.java:

package com.hw.Graph;

import java.util.HashMap;
import java.util.HashSet;

public class Graph {
    public HashMap<Integer, Node> nodes; //通过结点上的数值访问该结点
    public HashSet<Edge> edges; //存储图的所有边
    
    public Graph() {
        nodes = new HashMap<>();
        edges = new HashSet<>();
    }
}

好了，拥有了这些，我们就可以编写一些图的基本算法了。但是，就这样，我们怎样才能创建一个图呢？而且图的创建方式有许多种，有没有什么方式，在面对不管是以何种方式创建的图时，我们总能快速地把它转化为我们熟悉的结构，并使用我们自己编写的算法对于进行测试？肯定是有的。

我们不妨统一一下，以后在创建图时，我们用一个二维数组来存储，二维数组实际是一个一维数组，只是这个一维数组存储的每一个元素都是另一个一维数组。所以，在这个二维数组的每一个一维数组中，我们存储三个数据，分别是：开始结点的数值，结束结点的数值，这条边的权重。例如：

 

 

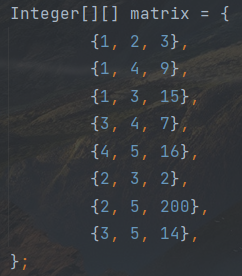
 这就表示这个图一共有8条边，第一条边的起始结点是1和2，这条边的权值是3...以此类推。而这个图创建出来，以可视化的形式表示则是下面这样的：

 

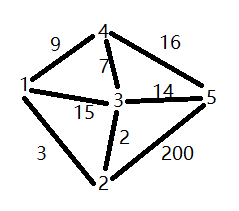
 接下来，我们来看看如何在拥有了以上三个基础类之后创建一个图：

 GraphGenerator.java:

package com.hw.Graph;

public class GraphGenerator {
    public static Graph createGraph(Integer[][] matrix) {
        Graph graph = new Graph();
        for (int i = 0; i < matrix.length; ++i) {
            int from = matrix[i][0];
            int to = matrix[i][1];
            int weight = matrix[i][2];
            
            //首先，我们往这个图中添加结点
            //如果不存在结点，就添加进去
            if (!graph.nodes.containsKey(from)) {
                graph.nodes.put(from, new Node(from));
            }
            if (!graph.nodes.containsKey(to)) {
                graph.nodes.put(to, new Node(to));
            }
            
            //现在创建一条边
            //当前前提是我们要先拿到这条边的两个结点
            Node fromNode = graph.nodes.get(from);
            Node toNode = graph.nodes.get(to);
            Edge newEdge = new Edge(fromNode, toNode, weight);
            
            //我们假设这个图是个有向图，当然，就算不是也没关系，按照无向图的处理方式处理就好了
            //如何处理？例如下面这行代码反着再写一遍
            //现在，因为从起始节点可以通过边找到末尾节点，因此：
            fromNode.nexts.add(toNode);
            
            //起始结点的出度+1：
            ++fromNode.out;
            //末尾结点的入度+1:
            ++toNode.in;
            
            //别忘了，结点还有一个边的属性：
            //由于从起始结点可以找到末尾结点，因此这条边应该属于起始结点：
            fromNode.edges.add(newEdge);
            
            //现在离成功只差最后一步，我们把这条边添加到这个图里：
            graph.edges.add(newEdge);
        }
        //最后，把这个图返回，就大功告成了
        return graph;
    }
}

上面的代码中，from，to和weight是我们事先说好的。

这样，一个图就创建好了。而且以后不管拿到一个以什么样的图，我们都可以像这样把它转化为我们熟悉的方式。

好了，接下来，我们来尝试编写图的广度优先算法：

首先我们需要一个队列，因为是广度优先，我们创建的这个方法需要先传一个结点过来，把这个结点放进队列，然后获取它的所有邻居结点，然后也全部放进队列，如此循环往复。由于队列是先进先出的结构，因此这样做可以做到遍历图时以“广度”优先。然后我们还需要一个访问数组，由于在取得结点邻居的过程中，我们不可避免地会重复访问结点，所以我们需要设置一个访问数组，对于已访问的结点，我们不做任何操作。

package com.hw.Graph;

import java.util.HashSet;
import java.util.LinkedList;
import java.util.Queue;

public class BFS {
    public static void bfs(Node node) {
        if (node == null) {
            return;
        }
        HashSet<Node> set = new HashSet<>();
        Queue<Node> queue = new LinkedList<>();
        //首先把传过来的结点添加进队列
        queue.offer(node);
        //这个set相当于一个访问数组，我们同样也把结点添加进数组中
        set.add(node);
        while(!queue.isEmpty())
        {
            //把这个结点弹出来
            Node cur = queue.poll();
            //这里对结点进行操作
            System.out.print(cur.value + " ");
            //遍历这个结点的所有可以通向的结点,广度优先的思想在这里就体现出来了
            for (Node nextNode : cur.nexts) {
                //我们肯定只能访问没有访问过的
                if (!set.contains(nextNode)) {
                    queue.offer(nextNode);
                    set.add(nextNode);
                }
             }
        }
        //循环结束后，所有结点就都被访问过了
        //我们在这里换个行，优化输出格式
        System.out.println();
    }
}

现在，我们可以试着测试一下这个图。

为了测试，我创建了一个新图：

package com.hw.Graph;

public class TestGraph {
    public static void main(String[] args) {
        Integer[][] matrix = {
                {1, 2, 8},
                {1, 3, 10},
                {2, 3, 5},
                {2, 5, 21},
                {3, 5, 4},
                {3, 4, 2},
                {5, 6, 1},
                {4, 6, 7},
        };
        Graph graph = GraphGenerator.createGraph(matrix);
        Node root = graph.nodes.get(1);
        BFS.bfs(root);
    }
}

这个图长这样：

 

结果如下：

 

 

 Perfect!

 现在我们来编写深度优先遍历算法：

在这之前呢，为了比较方便地表示图，我把用来表示图的每个结点的数字换成了相应的大写字符，例如1：A，2：B这样。改动很简单，相信我们都可以做到。

深度优先与广度优先类似，只是需要把广度优先使用的队列换成栈。我们先来看看代码：

package com.hw.Graph;

import java.util.HashSet;
import java.util.Stack;

public class DFS {
    public static void dfs(Node node) {
        if (node == null) {
            return;
        }
        Stack<Node> stack = new Stack<>();
        HashSet<Node> set = new HashSet<>();
        stack.push(node);
        set.add(node);
        System.out.print(node.value + " ");
        while(!stack.isEmpty())
        {
            Node cur = stack.pop();
            for (Node temp : cur.nexts) {
                if (!set.contains(temp)) {
                    stack.push(cur);
                    stack.push(temp);
                    set.add(temp);
                    System.out.print(temp.value + " ");
                    break;
                }
            }
        }
        System.out.println();
    }
}

重点解释一下while循环里的代码：

我在循环外面弄进去了传过来的数据，然后在循环里面把它拿出来，访问他所有的邻居，这个时候，如果没有被访问过，我把这个数据和访问到的它的第一个邻居，又放回栈里，然后break掉。这是因为我现在是深度优先，所以我需要拿到一结点，我就不停地向它的深度挖去，如果不break掉，就相当于这个结点的深度还没挖到底，我就换另外一条路了挖了。而从栈中拿出来又放回去，其实这样子等图中所有结点都遍历完后，栈中的顺序，就是深度优先的顺序。到最后，栈中的元素会一个一个弹出去，倘若其中有一条路还没走完，那么就会从返回的深度继续深度优先，而这时候，要做到从返回的深度开始，栈就是必须的。因此才需要拿出来又放回去的骚操作。

我们来看看效果：

 

 

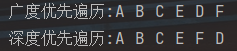
 Perfect!

接下来，我们不妨来看看图的普里姆算法。

普里姆算法的作用就是求解图的最小生成树。

主要算法思路就是，我从某一个结点开始，在与其所有相连的边中寻找一条权值最短的边，然后把这条边加进来，这条边另一端的结点也加进来。然后再次寻找权值最小的边添加进来，同时还要注意不能生成回路。其中，我选择的权值最小的边，是从与所有我已经添加进来的结点相连的边中，选择一条权值最小的边，并没有局限与哪个结点。

我们来看看代码：

package com.hw.Graph;

import java.util.Comparator;
import java.util.HashSet;
import java.util.PriorityQueue;

public class Prim {
    private static class EdgeComparator implements Comparator<Edge> {
        @Override
        public int compare(Edge o1, Edge o2) {
            // TODO Auto-generated method stub
            return o1.weight - o2.weight;
        }
    }
    
    public static void prim(Graph graph) {
        //我们创建这个小顶堆，作用是对所有边进行排序
        PriorityQueue<Edge> queue = new PriorityQueue<>(new EdgeComparator());
        HashSet<Node> set = new HashSet<>();
        //首先我们要拿到所有的点，这样才能拿到所有的边
        for (Node node : graph.nodes.values()) {
            //如果不在set中，就添加进去
            if (!set.contains(node)) {
                set.add(node);
                //现在，我们可以访问边了
                for (Edge edge : node.edges) {
                    //拿到边怎么办呢？当然是全部扔进小顶堆里排序
                    queue.offer(edge);
                }
                //好，现在排完序了，我们拿出一条边，这条边就是我们要找的
                //因为已经排过序了
                while(!queue.isEmpty())
                {
                    Edge edge = queue.poll();
                    //现在我们要得到这条边另一端的结点
                    //因为我们需要把那个结点加到集合里，防止形成环
                    Node toNode = edge.to;
                    if (!set.contains(toNode)) {
                        set.add(toNode);
                        System.out.println(edge);
                        //现在，我以toNode为基准，把它的所有边再加进堆中，全部重新排序
                        //如果不这么干，那么队列中的边将永远只有那么几条
                        for (Edge nextEdges : toNode.edges) {
                            queue.offer(nextEdges);
                        }
                    }
                }
            }
        }
    }
}

效果：

 

 Perfect!