[Contest1351]一样远

题面

Description

【问题描述】

企鹅国的城市结构是一棵树，有N座城市和N-1条无向道路，每条道路都一样长。豆豆和豆沙准备去参加NOIP（National Olympiad in Informatics for Penguin），但是他们住在不同的地方，豆豆住在城市A，豆沙住在城市B。他们想找一个距离A和B一样远的集合地点，所以他们想知道有多少个城市满足这个要求？

由于他们会参加很多次NOIP，所以有很多个询问。

 

【输入格式】

第一行一个整数N代表城市个数。

接下来N-1行，每行两个数字F和T，表示城市F和城市T之间有一条道路。

接下来一行一个整数M代表询问次数。

接下来M行，每行两个数字A和B，表示这次询问的城市A和城市B（A可能与B相同）。

 

【输出格式】

输出M行，每行一个整数表示到A和B一样远的城市个数。

 

【输入样例1】

4

1 2

2 3

2 4

2

1 2

1 3

 

【输出样例1】

0

2

【输入样例2】

4

1 2

2 3

2 4

2

1 1

3 3

【输出样例2】

4

4

 

【数据范围】

对于30%的数据：N,M≤1000；

对于另外10%的数据：A=B；

对于另外30%的数据：保证树的形态随机；

对于100%的数据：1≤N,M≤100000。

题意

有一颗树，每次选两个点，问你树上距离这两个点距离相等的点有几个。

题解

分类讨论一下：

①两个点相同，答案为$n$

②两个点与$lca$的距离之和（见下图）为奇数，不存在符合要求的点，答案为0

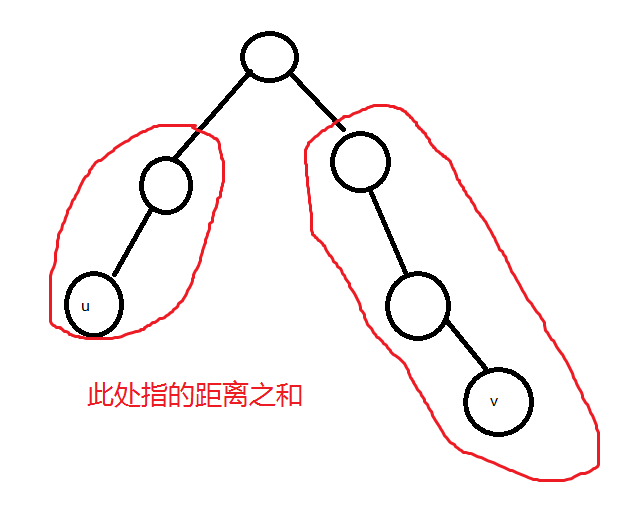
③除去上面两种情况，若两点距离相等，答案为$n$-两点路径上比$lca$深度大1的点的$size$

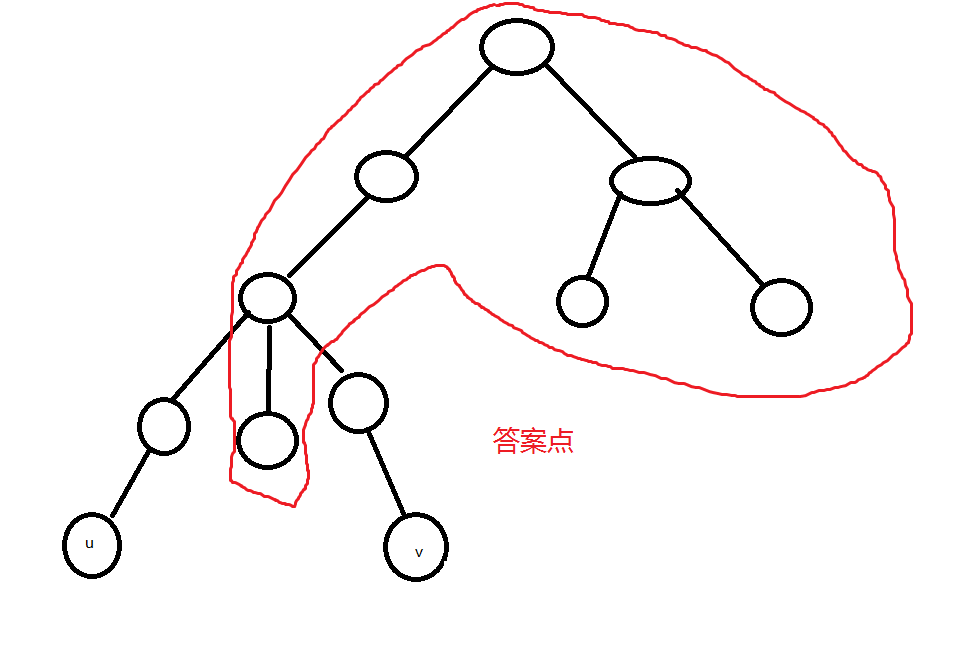
④两点深度不一样，记录深度较大的点往上跳$len$个点的点（中点）$x$和往上跳$len-1$个点的点$y$（$len$指两点与$lca$的距离之和），答案为$size_{x}-size_{y}$

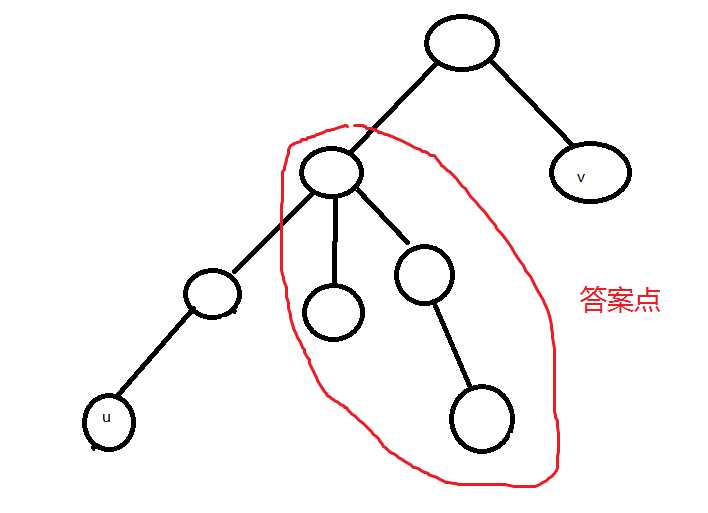
完事儿，上代码

#include<iostream>
using namespace std;
const int N=1e5+5;
int n,head[N],m,siz[N],f[N][25],d[N],cnt;
struct edge{
	int v,next;
}e[N<<1];
void add(int u,int v){
	e[++cnt]=(edge){v,head[u]};
	head[u]=cnt;
}
void dfs(int u,int fa){
	siz[u]=1;
	for(int i=head[u];i;i=e[i].next){
		int v=e[i].v;
		if(v==fa)continue;
		f[v][0]=u;
		d[v]=d[u]+1;
		dfs(v,u);
		siz[u]+=siz[v];
	}
}
int lca(int x,int y){
	if(d[x]<d[y])swap(x,y);
	for(int i=20;i>=0;i--)if(d[f[x][i]]>=d[y])x=f[x][i];
	if(x==y)return x;
	for(int i=20;i>=0;i--){
		if(f[x][i]!=f[y][i]){
			x=f[x][i];
			y=f[y][i];
		}
	}
	return f[x][0];
}
int main(){
	scanf("%d",&n);
	for(int i=1;i<n;i++){
		int u,v;
		scanf("%d%d",&u,&v);
		add(u,v);
		add(v,u);
	}
	dfs(1,0);
	for(int i=1;i<=20;i++){
		for(int j=1;j<=n;j++){
			f[j][i]=f[f[j][i-1]][i-1];
		}
	}
	scanf("%d",&m);
	while(m--){
		int u,v;
		scanf("%d%d",&u,&v);
		if(u==v)printf("%d\n",n);//情况1
		else{
			int x=lca(u,v);
			int len=d[u]+d[v]-2*d[x];
			if(len%2)printf("0\n");//情况2
			else{
				if(d[u]==d[v]){//情况3
					int y=u,z=v;
					for(int i=20;i>=0;i--)if(d[f[y][i]]>d[x])y=f[y][i];
					for(int i=20;i>=0;i--)if(d[f[z][i]]>d[x])z=f[z][i];
					printf("%d\n",n-siz[y]-siz[z]);
				}
				else{//情况4
					if(d[u]<d[v])swap(u,v);
					len/=2;//注意
					int y=u,z=u;
					for(int i=20;i>=0;i--)if((len-1)&(1<<i))y=f[y][i];
					for(int i=20;i>=0;i--)if(len&(1<<i))z=f[z][i];
					printf("%d\n",siz[z]-siz[y]);
				}
			}
		}
	}
}