2016年北大高代考研题解答

正十二面体有$12$个面,每个面为正五边形,每个顶点连接$3$条棱.求它的内切球与外接球半径比.

---

 

解.不妨设正十二面体的棱长均为$a$.

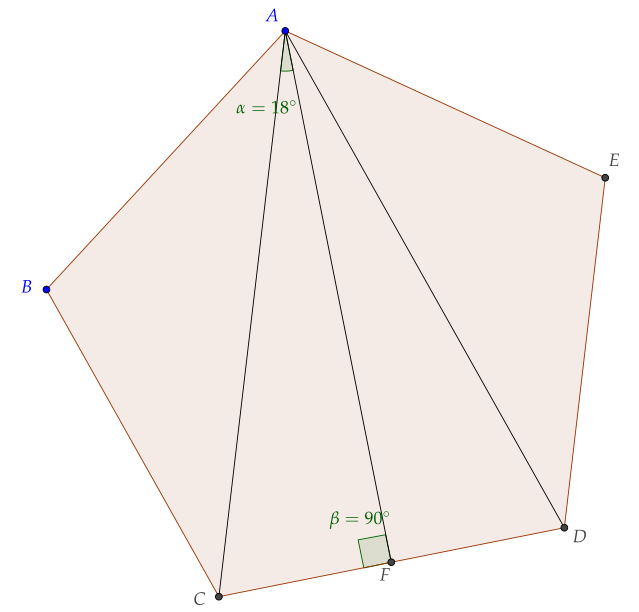
先求正五边形的高.如图所示,这里的字母记号和下图有冲突,请注意区别.利用这么个事实,从正五边形某个顶点向两个对点连线,这两条线将会三等分内角$\displaystyle \frac{(5-2)\times 180^\circ}5=108^\circ$,则三等分后的角$\angle CAD=36^\circ$,则$\angle CAF=18^\circ$,因此正五边形的高为
$$h=\frac{a/2}{\tan 18^{\circ}}=\frac{a/2}{\tan \left( \pi /10 \right)}=\frac{1}{2}\sqrt{5+2\sqrt{5}}a.$$

接着求正十二面体的二面角,记某顶点处的三条等长的棱形成的向量分别为$\vec{a},\vec{b},\vec{c}$,其中的任意两个向量夹角为$108^\circ$.

事实上,利用Lagrange恒等式 $$\left(\overrightarrow{a}\times\overrightarrow{b}\right)\cdot\left(\overrightarrow{c}\times\overrightarrow{d}\right)=\left|\begin{matrix}\overrightarrow{a}\cdot\overrightarrow{c}& \overrightarrow{a}\cdot\overrightarrow{d}\\\overrightarrow{b}\cdot\overrightarrow{c}& \overrightarrow{b}\cdot\overrightarrow{d}\\\end{matrix}\right|,$$ 我们有
$$\begin{align*} \frac{\left( \overrightarrow{a}\times \overrightarrow{b} \right) \cdot \left( \overrightarrow{b}\times \overrightarrow{c} \right)}{\left| \overrightarrow{a}\times \overrightarrow{b} \right|\left| \overrightarrow{b}\times \overrightarrow{c} \right|}&=\frac{1}{\left| \overrightarrow{a}\times \overrightarrow{b} \right|\left| \overrightarrow{b}\times \overrightarrow{c} \right|}\left| \begin{matrix} \overrightarrow{a}\cdot \overrightarrow{b}& \overrightarrow{a}\cdot \overrightarrow{c}\\ \overrightarrow{b}\cdot \overrightarrow{b}& \overrightarrow{b}\cdot \overrightarrow{c}\\ \end{matrix} \right|\\ &=\frac{1}{a^4\sin 108^{\circ}}\left| \begin{matrix} a^2\cos 108^{\circ}& a^2\cos 108^{\circ}\\ a^2& a^2\cos 108^{\circ}\\ \end{matrix} \right|\\ &=\frac{\cos ^2108^{\circ}-\cos 108^{\circ}}{\sin 108^{\circ}}=\frac{1}{\sqrt{5}}, \end{align*}$$
这里利用了
$$\cos 108^{\circ}=\frac{1-\sqrt{5}}{4},\qquad \sin 108^{\circ}=\sqrt{\frac{5+\sqrt{5}}{8}}.$$
由正十二面体实物图可以看出二面角显然为钝角,因此所求二面角$\theta$的余弦值为$\displaystyle \frac{1}{\sqrt{5}}$.

这题关键是找到适合计算的截面图,因为建坐标系比较复杂,利用坐标系不太现实.不过在英文Wiki上有这些坐标参数,利用这些数据此问题瞬间得到解答.如图便是我们找到的可行截面图,也就是$AC=h=\frac{1}{2}\sqrt{5+2\sqrt{5}}a$,且$\angle ACO=\gamma=\theta/2$.我们有
$$\cos \theta =-\frac{1}{\sqrt{5}}=1-2\sin ^2\gamma \Rightarrow \sin \gamma =\sqrt{\frac{5+\sqrt{5}}{10}},\cos \gamma =\sqrt{\frac{5-\sqrt{5}}{10}}.$$
因此梯形的下底为
$$\begin{align*} CF&=2CH+a=2h\cos \gamma +a\\ &=2\times \frac{1}{2}\sqrt{5+2\sqrt{5}}a\times \sqrt{\frac{5-\sqrt{5}}{10}}+a=\frac{3+\sqrt{5}}{2}a. \end{align*}$$
由此得
$$r=OI=\frac{CF}{2}\sin \gamma =\frac{3+\sqrt{5}}{4}a\times \sqrt{\frac{5+\sqrt{5}}{10}}=\frac{1}{2}\sqrt{\frac{25+11\sqrt{5}}{10}}a,$$
而由余弦定理可知
$$\begin{align*} R^2&=OA^2=h^2+\left( \frac{CF}{2} \right) ^2-2h\cdot \frac{CF}{2}\cdot \cos \gamma\\ &=\left( \frac{1}{2}\sqrt{5+2\sqrt{5}}a \right) ^2+\left( \frac{3+\sqrt{5}}{4}a \right) ^2-\sqrt{5+2\sqrt{5}}\times \frac{3+\sqrt{5}}{4}a\times \sqrt{\frac{5-\sqrt{5}}{10}}\\ &=\frac{9+3\sqrt{5}}{8}a^2, \end{align*}$$
即 $$R=\frac{\sqrt{3}+\sqrt{15}}{4}a,$$
从而所求内切球与外接球半径比等于
$$\frac{r}{R}=\frac{\frac{1}{2}\sqrt{\frac{25+11\sqrt{5}}{10}}a}{\frac{\sqrt{3}+\sqrt{15}}{4}a}=\sqrt{\frac{5+2\sqrt{5}}{15}}.$$
注:其实一开始我把$-\frac1{\sqrt{5}}$的负号丢了,折腾了半天.此外,我们还可以计算出正十二面体的表面积$S$和体积$V$分别为
$$S=3\sqrt{25+10\sqrt{5}}a^2,\qquad V=\frac{15+7\sqrt{5}}{4}a^3.$$