(PS:本文会不断更新)
\newcommand\R{\operatorname{Res}}
如何计算\zeta(2)=\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\cdotsζ(2)=112+122+132+⋯? 这个问题是在1644年由意大利数学家蒙哥利(Pietro Mengoli)提出的,而大数学家欧拉于1735年第一次解决了这个问题。他得出著名的结果:
\sum_{k=1}^{\infty}\frac{1}{k^2}=\frac{\pi^2}{6}∑k=1∞1k2=π26
解决这个问题的方法在近代不断涌现。这里我从各处摘抄到一些方法,列举在此,仅供大家参考。
如有错误,请向我指出,谢谢!(PS:最近发现忻州师范学院某网页抄了我博客后不给Reference,希望大家明辨是非)
首先,我们需要知道这个问题的等价形式,将这个数列除以4,我们自然得到\sum_{k=1}^{\infty} \frac{1}{(2k)^2}=\frac{\pi^2}{24}∑k=1∞1(2k)2=π224,从而我们只需证明
\sum_{k=1}^{\infty}\frac{1}{(2k-1)^2}=\frac{\pi^2}{8}∑k=1∞1(2k−1)2=π28
而以下某些证明会用到这一点。
证明1:欧拉的证明
欧拉的证明是十分聪明的。他只是将幂级数同有限的多项式联系到了一起,就得到了答案。首先注意到
\sin(x) = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdotssin(x)=x−x33!+x55!−x77!+⋯
从而
\frac{\sin(x)}{x} = 1 - \frac{x^2}{3!} + \frac{x^4}{5!} - \frac{x^6}{7!} + \cdotssin(x)x=1−x23!+x45!−x67!+⋯
但是\frac{\sin{x}}{x}sinxx的根集,为
x=n\cdot \pi,\mbox{ }(n = \pm1, \pm2, \pm3, \dots).x=n⋅π, (n=±1,±2,±3,…).
故我们可以假定
\begin{align} \frac{\sin(x)}{x} & {} = \left(1 - \frac{x}{\pi}\right)\left(1 + \frac{x}{\pi}\right)\left(1 - \frac{x}{2\pi}\right)\left(1 + \frac{x}{2\pi}\right)\left(1 - \frac{x}{3\pi}\right)\left(1 + \frac{x}{3\pi}\right) \cdots \notag\\ & {} = \left(1 - \frac{x^2}{\pi^2}\right)\left(1 - \frac{x^2}{4\pi^2}\right)\left(1 - \frac{x^2}{9\pi^2}\right) \notag\cdots. \end{align}sin(x)x=(1−xπ)(1+xπ)(1−x2π)(1+x2π)(1−x3π)(1+x3π)⋯=(1−x2π2)(1−x24π2)(1−x29π2)⋯.
(PS:欧拉似乎没有证明这个无穷积,直到100年后魏尔斯特拉斯得到了他著名的“魏尔斯特拉斯分解定理”(Weierstrass factorization theorem,详情可见wiki相应条目)。利用这个方法得到函数时要特别小心,我以前看到的一个反例就可以说明这个问题)
从而我们对这个无穷乘积的x^2x2项进行研究,可以知道
-\left(\frac{1}{\pi^2} + \frac{1}{4\pi^2} + \frac{1}{9\pi^2} + \cdots \right) = -\frac{1}{\pi^2}\sum_{n=1}^{\infty}\frac{1}{n^2}.−(1π2+14π2+19π2+⋯)=−1π2∑n=1∞1n2.
所以
-\frac{1}{6} = -\frac{1}{\pi^2}\sum_{n=1}^{\infty}\frac{1}{n^2}.−16=−1π2∑n=1∞1n2.
这样就得到了答案。
注:欧拉给出过严谨的证明,但是由于他的第一个证明太广为人知,所以有时候会认为他没给出真正的证明。不过贴吧里的 tq唐乾 吧友提醒了我,实际上,欧拉有他真正的证明。是通过如下方式:首先令NN为奇数
z^n-a^n=(z-1)\prod_{k=1}^{(n-1)/2}(z^2-2az\cos{\frac{2k\pi}{n}}+a^2)zn−an=(z−1)∏k=1(n−1)/2(z2−2azcos2kπn+a2)
令z=1+x/N,a=1-x/Nz=1+x/N,a=1−x/N,且n=N,有
\begin{align*}\left(1+\frac{x}N\right)^N-\left(1+\frac{x}N\right)^N &=\frac{2x}{N}\prod_{k=1}^{(N-1)/2}\left(2+\frac{2x^2}{N^2}-2\left(1-\frac{x^2}{N^2}\right)\cos{\frac{2k\pi}{N}}\right)\\ &=\frac{2x}{N}\prod_{k=1}^{(N-1)/2}\left(\left(1-\cos{\frac{2k\pi}{N}}\right)+\frac{x^2}{N^2}\left(1+\cos{\frac{2k\pi}{N}}\right)\right)\\ &=C_N x \prod_{k=1}^{(N-1)/2}\left(1+\frac{x^2}{N^2}\frac{1+\cos{(2k\pi/N)}}{1-\cos{(2k\pi/N)}}\right) \end{align*}(1+xN)N−(1+xN)N=2xN∏k=1(N−1)/2(2+2x2N2−2(1−x2N2)cos2kπN)=2xN∏k=1(N−1)/2((1−cos2kπN)+x2N2(1+cos2kπN))=CNx∏k=1(N−1)/2(1+x2N21+cos(2kπ/N)1−cos(2kπ/N))
考虑一次项系数知道C_N=2CN=2成立,而在N\to\inftyN→∞时,左边是e^x-e^{-x}ex−e−x,右边通过\cos{y}\approx 1-y^2/2cosy≈1−y2/2,那么右边就是1+x^2/(k^2\pi^2)1+x2/(k2π2)的乘积,也就是
\frac{e^x-e^{-x}}{2}=x\prod_{k=1}^{\infty}\left(1+\frac{x^2}{k^2\pi^2}\right)ex−e−x2=x∏k=1∞(1+x2k2π2)
比较三次项系数可知答案
证明2:一个初等的证明
以下证明第一次来自Ioannis Papadimitriou于1973年在American Math Monthly 80(4):424-425页发表的。Apostol在同一份杂志425-430发表了用这个方法计算\zeta(2n)ζ(2n)的方法。
这似乎是这个问题最“初等”的一个证明了,只需要知道三角函数相应知识就能够完成。我们先证明一个恒等式:
Lemma: 令\omega_m = \frac{\pi}{2m+1}ωm=π2m+1,则
\cot^2{\omega_m}+\cot^2{(2\omega_m)}+\cdots\cot^2{(m\omega_m)}=\frac{m(2m-1)}{3}.cot2ωm+cot2(2ωm)+⋯cot2(mωm)=m(2m−1)3.
证明:由于
\begin{align*} \sin{n\theta}&=\binom{n}{1}\sin{\theta}\cos^{n-1}{\theta}-\binom{n}{3}\sin^3{\theta}\cos^{n-3}{\theta}+\cdots \pm \sin^n{\theta}\\ &=\sin^n{\theta}\left(\binom{n}{1}\cot^{n-1}{\theta}-\binom{n}{3}\cot^{n-3}{\theta}+\cdots \pm 1\right) \end{align*}sinnθ=(n1)sinθcosn−1θ−(n3)sin3θcosn−3θ+⋯±sinnθ=sinnθ((n1)cotn−1θ−(n3)cotn−3θ+⋯±1)
很显然,令n=2m+1n=2m+1,则我们有\cot^2{\omega_m},\cot^2{(2\omega_m)}\cdots \cot^2{(m\omega_m)}cot2ωm,cot2(2ωm)⋯cot2(mωm)为多项式
\binom{n}{1}x^{m}-\binom{n}{3}x^{m-1}+\cdots \pm 1(n1)xm−(n3)xm−1+⋯±1
的根。从而利用韦达定理我们就完成了引理的证明。\square◻
由于三角不等式 \sin{x}<x<\tan{x}sinx<x<tanx 在x\in(0,\pi/2)x∈(0,π/2)成立,我们知道了\cot^2{x}<\frac{1}{x^2}<1+\cot^2{x}cot2x<1x2<1+cot2x.对于\omega_m,2\omega_m\cdotsωm,2ωm⋯带入得到
\sum_{k=1}^{m}\cot^2{(k\omega_m)}<\sum_{k=1}^{m}\frac{1}{k^2\omega_m^2}<m+\sum_{k=1}^{m}\cot^2{(k\omega_m)}∑k=1mcot2(kωm)<∑k=1m1k2ωm2<m+∑k=1mcot2(kωm)
所以应用上面引理,就可以得到
\frac{m(2m-1)\pi^2}{3(2m+1)^2}<\sum_{k=1}^{m}\frac{1}{k^2}<\frac{m(2m-1)\pi^2}{3(2m+1)^2}+\frac{m\pi^2}{(2m+1)^2}m(2m−1)π23(2m+1)2<∑k=1m1k2<m(2m−1)π23(2m+1)2+mπ2(2m+1)2
令m趋于无穷大,结论自然就成立了。
证明3:数学分析的证明
这个证明来自Apostol在1983年的“Mathematical Intelligencer”,只需要简单的高数知识。
注意到恒等式
\frac{1}{n^2}=\int_{0}^1\int_0^1 x^{n-1}y^{n-1}dxdy1n2=∫01∫01xn−1yn−1dxdy
利用单调收敛定理(Monotone Convergence Theorem),立即得到
\sum_{n=1}^{\infty}\frac{1}{n^2}=\int_{0}^1\int_0^1\left(\sum_{n=1}^{\infty}(xy)^{n-1}\right)dxdy=\int_{0}^1\int_0^1 \frac{1}{1-xy}dxdy∑n=1∞1n2=∫01∫01(∑n=1∞(xy)n−1)dxdy=∫01∫0111−xydxdy
通过换元(u,v)=((x+y)/2,(y-x)/2)(u,v)=((x+y)/2,(y−x)/2),也就是(x,y)=(u-v,u+v)(x,y)=(u−v,u+v)故
\sum_{n=1}^{\infty}\frac{1}{n^2}=2\iint_S\frac{1}{1-u^2+v^2}dudv∑n=1∞1n2=2∬S11−u2+v2dudv
SS是由点(0,0),(1/2,-1/2),(1,0),(1/2,1/2)(0,0),(1/2,−1/2),(1,0),(1/2,1/2)构成的正方形,利用正方形的对称性,那么
\begin{align*} 2\iint_S\frac{1}{1-u^2+v^2}dudv&=4\int_{0}^{1/2}\int_{0}^{u}\frac{1}{1-u^2+v^2}dvdu+4\int_{1/2}^{1}\int_{0}^{1-u}\frac{1}{1-u^2+v^2}dvdu\\ &=4\int_{0}^{1/2}\frac{1}{\sqrt{1-u^2}}\arctan{\left(\frac{u}{\sqrt{1-u^2}}\right)}du\\&\quad+4\int_{1/2}^{1}\frac{1}{\sqrt{1-u^2}}\arctan{\left(\frac{1-u}{\sqrt{1-u^2}}\right)}du \end{align*}2∬S11−u2+v2dudv=4∫01/2∫0u11−u2+v2dvdu+4∫1/21∫01−u11−u2+v2dvdu=4∫01/211−u2arctan(u1−u2)du+4∫1/2111−u2arctan(1−u1−u2)du
利用恒等式\arctan{(u/\sqrt{1-u^2})}=\arcsin{u},\arctan{((1-u)/\sqrt{1-u^2})}=\frac{\pi}{4}-\frac{1}{2}\arcsin{u}arctan(u/1−u2)=arcsinu,arctan((1−u)/1−u2)=π4−12arcsinu,就能够得到
\begin{align*}\sum_{n=1}^{\infty}\frac{1}{n^2}&=4\int_0^{1/2}\frac{\arcsin{u}}{\sqrt{1-u^2}}du+4\int_{1/2}^{1}\frac{1}{\sqrt{1-u^2}}\left(\frac{\pi}{4}-\frac{\arcsin{u}}{2}\right)du\\ &=[2\arcsin{u}^2]_0^{1/2}+[\pi\arcsin{u}-\arcsin{u}^2]_{1/2}^{1}\\ &=\frac{\pi^2}{18}+\frac{\pi^2}{2}-\frac{\pi^2}{4}-\frac{\pi^2}{6}+\frac{\pi^2}{36}\\ &=\frac{\pi^2}{6} \end{align*}∑n=1∞1n2=4∫01/2arcsinu1−u2du+4∫1/2111−u2(π4−arcsinu2)du=[2arcsinu2]01/2+[πarcsinu−arcsinu2]1/21=π218+π22−π24−π26+π236=π26
证明4:数学分析的证明
(Calabi, Beukers & Kock.)同样利用上一问的结论,不过这次我们计算的是:
\sum_{n=0}^{\infty}\frac{1}{(2n+1)^2}=\int_0^1\int_0^1\frac{dxdy}{1-x^2y^2}∑n=0∞1(2n+1)2=∫01∫01dxdy1−x2y2
做代换
(u,v)=\left(\arctan{x}\sqrt{\frac{1-y^2}{1-x^2}},\arctan{x}\sqrt{\frac{1-x^2}{1-y^2}}\right)(u,v)=(arctanx1−y21−x2,arctanx1−x21−y2)
从而有(x,y)=\left(\frac{\sin{u}}{\cos{v}},\frac{\sin{v}}{\cos{u}}\right)(x,y)=(sinucosv,sinvcosu)
雅可比行列式即为
\begin{align*} \frac{\partial (x,y)}{\partial(u,v)}&=\begin{vmatrix} \cos{u}/\cos{v} & \sin{u}\sin{v}/\cos{v}^2 \\ \sin{u}\sin{v}/\cos{u}^2 & \cos{v}/\cos{u} \end{vmatrix}\\ &=1-\frac{\sin^2u\sin^2v}{\cos^2u\cos^2v}=1-x^2y^2 \end{align*}∂(x,y)∂(u,v)=|cosu/cosvsinusinv/cosv2sinusinv/cosu2cosv/cosu|=1−sin2usin2vcos2ucos2v=1−x2y2
从而
\frac{3}{4}\zeta(2)=\sum_{n=0}^{\infty}\frac{1}{(2n+1)^2}=\iint_{A}dudv34ζ(2)=∑n=0∞1(2n+1)2=∬Adudv
其中A=\{(u,v)|u>0,v>0,u+v<\frac{\pi}{2}\}A={(u,v)|u>0,v>0,u+v<π2},从而\zeta(2)=\frac{\pi^2}{6}ζ(2)=π26成立!\square◻
证明5:复分析的证明
这个证明在很多复分析书上都有。我们同样可以利用留数计算该结果,考虑f(x)=z^{-2} \cot{\pi z}f(x)=z−2cotπz,积分路径P_nPn为在中心为原点的长形如图
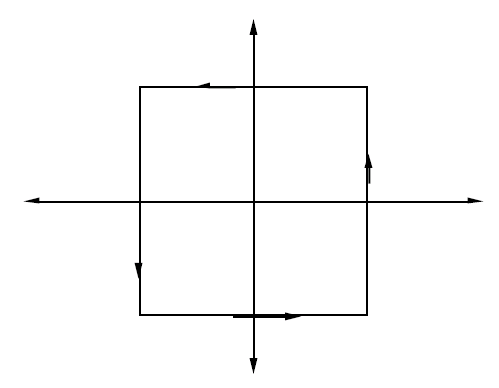
实轴交点为\pm(n+1/2)±(n+1/2),复轴为\pm ni±ni,而若\pi z=x+iyπz=x+iy,直接计算可得
|\cot{\pi z}|^2=\frac{\cos^2{x}+\sinh^2{y}}{\sin^2{x}+\sinh^2{y}}|cotπz|2=cos2x+sinh2ysin2x+sinh2y
,从而很容易就能知道|\cot{\pi z}|<2|cotπz|<2对于每根积分曲线成立,于此同时,|z|\ge n|z|≥n成立,从而有
\left|\oint_{P_n}z^{-2}\cot{\pi z}\right|\le\frac{2}{n^2}(8n+2)|∮Pnz−2cotπz|≤2n2(8n+2)
成立,在n\to\inftyn→∞时,该积分值趋于00.
利用留数定理,则有
2\pi i\sum_{k=-\infty}^{\infty}\R(z^{-2}\cot{\pi z},k)=\lim_{n\to\infty}\oint_{P_n}z^{-2}\cot{\pi z}dz=02πi∑k=−∞∞Res(z−2cotπz,k)=limn→∞∮Pnz−2cotπzdz=0
而每一点的留数,计算有\R(z^{-2}\cot{\pi z},0)=-\pi/3Res(z−2cotπz,0)=−π/3,\R(z^{-2}\cot{\pi z},k)=1/(\pi k^2)(k\not=0,k\in\mathbb{Z})Res(z−2cotπz,k)=1/(πk2)(k≠0,k∈Z),从而有
\sum_{k=1}^{\infty}\frac{2}{\pi k^2}=\frac{\pi}{3}∑k=1∞2πk2=π3
答案显而易见了。
证明6:复数积分的证明
本证明由Dennis C.Russell给出。考虑积分
I=\int_0^{\pi/2}\ln(2\cos{x})dxI=∫0π/2ln(2cosx)dx
那么利用\coscos的欧拉公式
2\cos{x}=e^{ix}+e^{-ix}=e^{ix}(1+e^{-2ix})2cosx=eix+e−ix=eix(1+e−2ix)从而\ln(2\cos{x})=\ln(e^{ix})+\ln(1+e^{-2ix})=ix+\ln(1+e^{-2ix})ln(2cosx)=ln(eix)+ln(1+e−2ix)=ix+ln(1+e−2ix)在积分中代换得
\begin{align*} I&=\int_0^{\pi/2}ix+\ln(1+e^{-2ix})dx\\&=i\frac{\pi^2}{8}+\int_0^{\pi/2}ln(1+e^{-2ix})dx \end{align*}I=∫0π/2ix+ln(1+e−2ix)dx=iπ28+∫0π/2ln(1+e−2ix)dx
再利用\ln{(1+x)}ln(1+x)的泰勒展开,也就是
\ln(1+x)=x-x^2/2+x^3/3-x^4/4+\cdotsln(1+x)=x−x2/2+x3/3−x4/4+⋯
代入知为
\ln(1+e^{-2ix})=e^{2ix}-e^{-4ix}/2+e^{-6ix}/3+\cdotsln(1+e−2ix)=e2ix−e−4ix/2+e−6ix/3+⋯
从而积分就有
\int_0^{\pi/2}\ln{(1+e^{-2ix})}dx=-\frac{1}{2i}(e^{-i\pi}-1-\frac{e^{-2i\pi}-1}{2^2}+\frac{e^{-3i\pi}-1}{3^2}-\frac{e^{-4i\pi}-1}{4^2}+\cdots)∫0π/2ln(1+e−2ix)dx=−12i(e−iπ−1−e−2iπ−122+e−3iπ−132−e−4iπ−142+⋯)
但是由于e^{-i\pi}=-1e−iπ=−1,原式变为
\int_0^{\pi/2}\ln(1+e^{-2ix})dx=\frac{1}{i}\sum_{k=1}^{\infty}\frac{1}{(2k-1)^2}=\frac{-3i}{4}\zeta(2)∫0π/2ln(1+e−2ix)dx=1i∑k=1∞1(2k−1)2=−3i4ζ(2)
故如前面式子有
I=i\left(\frac{\pi^2}{8}+\frac{-3}{4}\zeta(2)\right)I=i(π28+−34ζ(2))
由于左边是实数,右边是纯虚数,从而只能两边都为0,即\zeta(2)=\frac{\pi^2}{6}ζ(2)=π26,这还给了我们一个副产品,就是
\int_0^{\pi/2}\ln(\cos{x})dx=-\frac{\pi}{2}\ln{2}∫0π/2ln(cosx)dx=−π2ln2
证明7:泰勒公式证明
(Boo Rim Choe 在1987 American Mathematical Monthly上发表)利用反三角函数\arcsin{x}arcsinx的泰勒展开
\arcsin{x}=\sum_{n=0}^{\infty}\frac{1\cdot 3\cdots (2n-1)}{2\cdot 4\cdots (2n)}\frac{x^{2n+1}}{2n+1}arcsinx=∑n=0∞1⋅3⋯(2n−1)2⋅4⋯(2n)x2n+12n+1
对于|x|\le 1|x|≤1成立,从而令x=\sin{t}x=sint,有
t=\sum_{n=0}^{\infty}\frac{1\cdot 3\cdots (2n-1)}{2\cdot 4\cdots (2n)}\frac{\sin^{2n+1}t}{2n+1}t=∑n=0∞1⋅3⋯(2n−1)2⋅4⋯(2n)sin2n+1t2n+1
对于|t|\le\frac{\pi}{2}|t|≤π2成立,但由于积分
\int_0^{\pi/2}\sin^{2n+1}{x}dx=\frac{2\cdot 4\cdots (2n)}{3\cdot 5\cdots (2n+1)}∫0π/2sin2n+1xdx=2⋅4⋯(2n)3⋅5⋯(2n+1)
故而对两边从00到\pi/2π/2积分有
\frac{\pi^2}{8}=\int_0^{\pi/2}tdt=\sum_{n=0}^{\infty}\frac{1}{(2n+1)^2}π28=∫0π/2tdt=∑n=0∞1(2n+1)2
同样可得
证明8:复分析证明
(T. Marshall 在American Math Monthly,2010)对于z\in D=\mathbb{C}\backslash\{0,1\}z∈D=C∖{0,1}, 令
R(z)=\sum\frac{1}{\log^2 z}R(z)=∑1log2z
这个和是对于每一个\loglog的分支加起来. 在 DD 中所有点有领域使\log(z)log(z)的分支解析.由于这个级数在 z=1z=1之外一致收敛, R(z)R(z)在 DD上解析.
这里有几个Claim:
- 当z\to0z→0时,级数每一项趋于00.由于一致收敛我们知道z=0z=0是可去奇点,我们可令R(0)=0R(0)=0.
- RR 的唯一奇点是 z=1z=1的二阶极点,是由 \log zlogz的主分支.我们有\lim_{z\to1}(z-1)^2R(z)=1limz→1(z−1)2R(z)=1.
- R(1/z)=R(z)R(1/z)=R(z).
由于 1.和 3.有 RR 在\mathbb{C}\cup \{\infty\}C∪{∞}(扩充复平面)上亚纯,从而是有理函数. 从2知道R(z)R(z)的分母是(z-1)^2(z−1)2. 由于R(0)=R(\infty)=0R(0)=R(∞)=0, 分子就是azaz. 而2. 说明a=1a=1, 也就是
R(z)=\frac{z}{(z-1)^2}.R(z)=z(z−1)2.
现在令z=e^{2\pi i w}z=e2πiw 得到
\sum\limits_{n=-\infty}^{\infty}\frac{1}{(w-n)^2}=\frac{\pi^2}{\sin^2(\pi w)}∑n=−∞∞1(w−n)2=π2sin2(πw)
也就是说
\sum\limits_{k=0}^{\infty}\frac{1}{(2k+1)^2}=\frac{\pi^2}{8},∑k=0∞1(2k+1)2=π28,
可立刻的到\zeta(2)=\pi^2/6ζ(2)=π2/6 .
证明9:傅立叶分析证明
考虑函数f(x)=x^2,x\in(-\pi,\pi)f(x)=x2,x∈(−π,π),将其傅立叶展开
f(x)=\dfrac{\pi ^{2}}{3}+\sum_{n=1}^{\infty }\left( (-1)^{n}\dfrac{4}{n^{2}} \cos nx\right)f(x)=π23+∑n=1∞((−1)n4n2cosnx)
显而易见,代入f(0)f(0)即可得到答案
证明10:傅立叶分析证明
考虑函数f(x)=x,x\in(-\pi,\pi)f(x)=x,x∈(−π,π),将其傅立叶展开
f(x)=2\sum_{n=1}^{\infty }\left( \dfrac{(-1)^{n+1}}{n} \sin nx\right)f(x)=2∑n=1∞((−1)n+1nsinnx)
利用Parseval等式
\sum_{n=1}^{\infty}|a_n|^2=\frac{1}{2\pi}\int_{-\pi}^{\pi}x^2dx∑n=1∞|an|2=12π∫−ππx2dx
其中a_nan为e^{inx}einx的系数,即\frac{(-1)^n}{n}i(−1)nni,a_0=0a0=0
那么有
2\sum_{k=1}^{\infty}\frac{1}{k^2}=\frac{1}{2\pi}\int_{-\pi}^{\pi}x^2dx2∑k=1∞1k2=12π∫−ππx2dx
可得答案
证明11:傅立叶分析证明
考虑
f(t)=\sum_{n=1}^{\infty}\frac{\cos{nt}}{n^2}f(t)=∑n=1∞cosntn2
在实轴上一致收敛,对于在t\in [-\epsilon,2\pi-\epsilon]t∈[−ϵ,2π−ϵ],我们有
\sum_{n=1}^N\sin{nt}=\frac{e^{it}-e^{i(N+1)t}}{2i(1-e^{it})}+\frac{1-e^{iN)t}}{2i(1-e^{it})}∑n=1Nsinnt=eit−ei(N+1)t2i(1−eit)+1−eiN)t2i(1−eit)
这个和被
\frac{2}{|1-e^{it}|}=\frac{1}{\sin{t/2}}2|1−eit|=1sint/2
控制,从而在[\epsilon,2\pi-\epsilon][ϵ,2π−ϵ]上一致有界,据Dirichlet判别法
\sum_{n=1}^{\infty}\frac{\sin{t}}{n}∑n=1∞sintn
是在[\epsilon,e\pi-\epsilon][ϵ,eπ−ϵ]一致收敛,从而对于t\in(0,2\pi)t∈(0,2π),
f'(t)=-\sum_{n=1}^{\infty}\frac{\sin{nt}}{n}=\Im(\log(1-e^{it}))=\arg{(1-e^{it})}=\frac{t-\pi}{2}f′(t)=−∑n=1∞sinntn=ℑ(log(1−eit))=arg(1−eit)=t−π2
从而有
-\zeta(2)/2-\zeta(2)=f(\pi)-f(0)=\int_0^\pi\frac{t-\pi}{2}dt=-\frac{\pi^2}{4}−ζ(2)/2−ζ(2)=f(π)−f(0)=∫0πt−π2dt=−π24
证明12:泊松公式证明
(Richard Troll)由泊松求和公式
\sum_{n=-\infty}^{\infty}f(n)=\sum_{k=-\infty}^{\infty}\hat{f}(k)∑n=−∞∞f(n)=∑k=−∞∞f^(k)
可知
其中\hat{f}(\xi)=\int_{-\infty}^{\infty}f(x) e^{-2\pi ix\xi}dxf^(ξ)=∫−∞∞f(x)e−2πixξdx为傅立叶变换。
那么有f(x)=e^{-a|x|}f(x)=e−a|x|,ff的傅立叶变换为
\hat{f}(\xi)=\frac{2a}{a^2+4\pi^2\xi^2}f^(ξ)=2aa2+4π2ξ2
也就是说
\frac{1}{2a}\sum_{n\in\mathbb{Z}}e^{-a|n|}-\frac{1}{a^2}=\sum_{k=1}^{\infty}\frac{2}{a^2+4\pi^2 k^2}12a∑n∈Ze−a|n|−1a2=∑k=1∞2a2+4π2k2
则
\lim_{a\to 0}\sum_{k=1}^{\infty}\frac{2}{a^2+4\pi^2 k^2}=\lim_{a\to 0}\left\{\frac{1}{2a}\left(\frac{e^a+1}{e^a-1}\right)-\frac{1}{a^2}\right\}=\frac{1}{12}lima→0∑k=1∞2a2+4π2k2=lima→0{12a(ea+1ea−1)−1a2}=112
从而就有\zeta(2)=\frac{\pi^2}{6}ζ(2)=π26
证明13:概率论证明
(Luigi Pace 发表于2011 American Math Monthly)
设X_1,X_2X1,X2是独立同半区域柯西分布,也就是它们的分布函数都是p(x)=\frac{2}{\pi(1+x^2)}(x>0)p(x)=2π(1+x2)(x>0)
令随机变量Y=X_1/X_2Y=X1/X2,那么YY的概率密度函数p_YpY定义在y>0y>0,有
\begin{align*}p_Y(y) &= \int_0^{\infty} x p_{X_1} (xy) p_{X_2}(x) dx = \frac{4}{\pi^2} \int_0^\infty \frac{x}{(1+x^2 y^2)(1+x^2)}dx\\ &=\frac{2}{\pi^2 (y^2-1)} \left[\log \left( \frac{1+x^2 y^2}{1+x^2}\right) \right]_{x=0}^{\infty} = \frac{2}{\pi^2} \frac{\log(y^2)}{y^2-1} = \frac{4}{\pi^2} \frac{\log(y)}{y^2-1}. \end{align*}pY(y)=∫0∞xpX1(xy)pX2(x)dx=4π2∫0∞x(1+x2y2)(1+x2)dx=2π2(y2−1)[log(1+x2y21+x2)]x=0∞=2π2log(y2)y2−1=4π2log(y)y2−1.
由于X_1,X_2X1,X2独立同分布,所以P(Y>1)=P(X_1>X_2)=1/2P(Y>1)=P(X1>X2)=1/2,那么有
\frac{1}{2}=\int_0^1\frac{4}{\pi^2}\frac{\log(y)}{y^2-1}dy12=∫014π2log(y)y2−1dy
也就是说
\frac{\pi^2}{8} = \int_0^1 \frac{-\log(y)}{1-y^2} dy = -\int_0^1 \log(y) (1+y^2+y^4 + \cdots) dy = \sum_{k=0}^\infty \frac{1}{(2k+1)^2}π28=∫01−log(y)1−y2dy=−∫01log(y)(1+y2+y4+⋯)dy=∑k=0∞1(2k+1)2
那么答案显而易见。
证明14:积分+函数方程证明
(H Haruki,S Haruki在1983年 American Mathematical Monthly发表)
由于
\sum_{n=1}^{\infty}\frac{1}{n^2}=\sum_{n=1}^{\infty}\frac{1}{n}\int_0^1 x^{n-1}dx=\int_0^1\frac{\log{(1-x)}}{x}dx∑n=1∞1n2=∑n=1∞1n∫01xn−1dx=∫01log(1−x)xdx
只需要算出这个积分值即可,我们令
f(a)=\int_0^1\frac{\log{(x^2-2x\cos{a}+1)}}{x}dxf(a)=∫01log(x2−2xcosa+1)xdx
要证明f(a)=-\frac{(a-\pi)^2}{2}+\frac{\pi^2}{6}f(a)=−(a−π)22+π26
利用等式(x^2-2x\cos{a}+1)(x^2+2x\cos{a}+1)=x^4-2x^2\cos{2a}+1(x2−2xcosa+1)(x2+2xcosa+1)=x4−2x2cos2a+1我们有
f(a/2)+f(\pi-a/2)=\int_0^1\frac{\log{(x^4-2x^2\cos{a}+1)}}{x}=\frac{1}{2}\frac{\log{(t^2-2t\cos{a}+1)}}{t}dt=\frac{1}{2}f(a)f(a/2)+f(π−a/2)=∫01log(x4−2x2cosa+1)x=12log(t2−2tcosa+1)tdt=12f(a)
中间是令\sqrt{x}=tx=t得到的等式。解函数方程f(a/2)+f(\pi-a/2)=f(a)/2f(a/2)+f(π−a/2)=f(a)/2,求导两次得f''(a/2)+f''(\pi-a/2)=2f''(a)f″(a/2)+f″(π−a/2)=2f″(a),由于f''f″是在闭区间[0,2\pi][0,2π]上的连续函数,从而f''f″在该区域有最大值MM与最小值mm.设f''(a_0)=Mf″(a0)=M对于某个a_0\in[0,2\pi]a0∈[0,2π]成立,在等式中设a=a_0a=a0有
f''(a_0/2)+f''(\pi-a_0/2)=2f''(a_0)=2Mf″(a0/2)+f″(π−a0/2)=2f″(a0)=2M
但是由于f''(a_0/2),f''(\pi-a_0/2)f″(a0/2),f″(π−a0/2)都小于MM,从而只能都等于MM.继续这样的迭代,就有
\lim_{n\to\infty} f''(a_0/2^n)=f''(0)=Mlimn→∞f″(a0/2n)=f″(0)=M
类似地,我们就有f''(0)=mf″(0)=m,从而M=mM=m,f''f″为常函数,则ff只能是二次函数,设
f(a)=\alpha \frac{a^2}{2}+\beta a+\gammaf(a)=αa22+βa+γ
代入式子有-\pi\alpha/2=\beta/2,\pi^2\alpha/2+\beta\pi+2\gamma=\gamma/2−πα/2=β/2,π2α/2+βπ+2γ=γ/2,而
f'(a)=\int_0^1\frac{2\sin{a}}{1+x^2-2x\cos{a}}dxf′(a)=∫012sina1+x2−2xcosadx
得知f'(\pi/2)=\pi/2f′(π/2)=π/2
从而有\alpha=-1,\beta=\pi,\gamma=-\pi^2/3α=−1,β=π,γ=−π2/3,代入a=0a=0,得到
\int_0^1\frac{\log{(1-x)}}{x}dx=-\frac{\pi^2}{6}∫01log(1−x)xdx=−π26
证明15:三角恒等式的初等证明
(Josef Hofbauer发表于2002年American Mathematical Monthly)
\frac{1}{\sin^2x}=\frac{1}{4\sin^2{\frac{x}{2}}\cos^2{\frac{x}{2}}}=\frac{1}{4}\left[\frac{1}{\sin^2{\frac{x}{2}}}+\frac{1}{\sin^2{\frac{\pi+x}{2}}}\right]1sin2x=14sin2x2cos2x2=14[1sin2x2+1sin2π+x2]
从而就有
1=\frac{1}{\sin^2{\frac{\pi}{2}}}=\frac{1}{4\left[\frac{1}{\sin^2{\frac{\pi}{4}}}+\frac{1}{\sin^2{\frac{3\pi}{4}}}\right]}=\cdots =\frac{1}{4^n}\sum_{k=0}^{2^n-1}\frac{1}{\sin^2{\frac{(2k+1)\pi}{2^{n+1}}}}=\frac{2}{4^n}\sum_{k=0}^{2^{n-1}-1}\frac{1}{\sin^2{\frac{(2k+1)\pi}{2^{n+1}}}}1=1sin2π2=14[1sin2π4+1sin23π4]=⋯=14n∑k=02n−11sin2(2k+1)π2n+1=24n∑k=02n−1−11sin2(2k+1)π2n+1
又由于\sin^{-2}x>x^{-2}>\tan^{-2}xsin−2x>x−2>tan−2x对x\in(0,\pi/2)x∈(0,π/2)成立
令x=(2k+1)\pi/(2N)x=(2k+1)π/(2N),对k=0,1,\cdots,N/2-1(N=2^n)k=0,1,⋯,N/2−1(N=2n)对不等式求和,就变为
1>\frac{8}{\pi^2}\sum_{k=0}^{2^n-1}\frac{1}{(2k+1)^2}>1-\frac{1}{N}1>8π2∑k=02n−11(2k+1)2>1−1N
令N\to\inftyN→∞可得答案
证明16:三角多项式的证明
(Kortram发表于1996年 Mathematics Magazine)
对于奇数n=2m+1n=2m+1,我们知道\sin{nx}=F_n(\sin{x})sinnx=Fn(sinx),其中F_nFn是次数nn的多项式。那么F_nFn的零点为\sin(j\pi/n)(-m\le j\le m)sin(jπ/n)(−m≤j≤m),且有\lim_{y\to 0}(F_n(y)/y)=nlimy→0(Fn(y)/y)=n.那么
F_n(y)=ny\prod_{j=1}^m\left(1-\frac{y^2}{\sin^2(j\pi/n)}\right)Fn(y)=ny∏j=1m(1−y2sin2(jπ/n))
从而
\sin{nx}=n\sin{x}\prod_{j=1}^m\left(1-\frac{\sin^2x}{\sin^2(j\pi/n)}\right)sinnx=nsinx∏j=1m(1−sin2xsin2(jπ/n))
比较两边泰勒展开的x^3x3系数,有
-\frac{n^3}{6}=-\frac{n}{6}-n\sum_{j=1}^{m}\frac{1}{\sin^2(j\pi/n)}−n36=−n6−n∑j=1m1sin2(jπ/n)
于是
\frac{1}{6}-\sum_{j=1}^m\frac{1}{n^2\sin^2(j\pi/n)}=\frac{1}{6n^2}16−∑j=1m1n2sin2(jπ/n)=16n2
固定整数MM,令m>Mm>M,则有
\frac{1}{6}-\sum_{j=1}^M\frac{1}{n^2\sin^2(j\pi/n)}=\frac{1}{6n^2}+\sum_{j=M+1}^m\frac{1}{n^2\sin^2(j\pi/n)}16−∑j=1M1n2sin2(jπ/n)=16n2+∑j=M+1m1n2sin2(jπ/n)
利用\sin{x}>\frac{2}{\pi}xsinx>2πx对于0<x<\frac{\pi}{2}0<x<π2成立,我们有
0<\frac{1}{6}-\sum_{j=1}^M\frac{1}{n^2\sin^2(j\pi/n)}=\frac{1}{6n^2}+\sum_{j=M+1}^m\frac{1}{4j^2}0<16−∑j=1M1n2sin2(jπ/n)=16n2+∑j=M+1m14j2
令n,mn,m趋于无穷,就有
0\le \frac{1}{6}-\sum_{j=1}^M\frac{1}{\pi^2j^2}\le \sum_{j=M+1}^m\frac{1}{4j^2}0≤16−∑j=1M1π2j2≤∑j=M+1m14j2
也即
\sum_{j=1}^{\infty}\frac{1}{\pi^2j^2}=\frac{1}{6}∑j=1∞1π2j2=16
证明17:积分证明
(Matsuoka发表于1961年American Mathematical Montly)
考虑积分
I_n=\int_0^{\pi/2}\cos^{2n}xdx\mbox{ and }J_n=\int_0^{\pi/2}x^2\cos^{2n}xdxIn=∫0π/2cos2nxdx and Jn=∫0π/2x2cos2nxdx
我们有Wallis公式:
I_n=\frac{1\cdot 3\cdot 5\cdots (2n-1)}{2\cdot 4\cdot 6\cdots 2n}\frac{\pi}{2}=\frac{(2n)!}{4^n(n!)^2}\frac{\pi}{2}In=1⋅3⋅5⋯(2n−1)2⋅4⋅6⋯2nπ2=(2n)!4n(n!)2π2
那么对于n>0n>0,分部积分有
\begin{align*} I_n&=[x\cos^{2n}x]_0^{\pi/2}+2n\int_0^{\pi/2}x\sin{x}\cos^{2n-1}xdx\\ &=n(2n-1)J_{n-1}-2n^2 J_n \end{align*}In=[xcos2nx]0π/2+2n∫0π/2xsinxcos2n−1xdx=n(2n−1)Jn−1−2n2Jn
从而有
\frac{(2n)!}{4^n(n!)^2}\frac{\pi}{2}=n(2n-1)J_{n-1}-2n^2 J_n(2n)!4n(n!)2π2=n(2n−1)Jn−1−2n2Jn
得到
\frac{\pi}{4n^2}=\frac{4^{n-1}(n-1)!^2}{(2n-2)!}J_{n-1}-\frac{4^nn!^2}{(2n)!}J_nπ4n2=4n−1(n−1)!2(2n−2)!Jn−1−4nn!2(2n)!Jn
将这个式子从1加到nn,能够有
\frac{\pi}{4}\sum_{n=1}^N\frac{1}{n^2}=J_0-\frac{4^N N!^2}{(2N)!}J_Nπ4∑n=1N1n2=J0−4NN!2(2N)!JN
由于J_0=\pi^3/24J0=π3/24,只需要证明\lim_{N\to\infty} 4^N N!^2 J_N/(2N)!=0limN→∞4NN!2JN/(2N)!=0,但是不等式x<\frac{\pi}{2}\sin{x}x<π2sinx对于0<x<\frac{\pi}{2}0<x<π2,得到
J_N<\frac{\pi^2}{4}\int_0^{\pi/2}\sin^2x\cos^{2N}xdx=\frac{\pi^2}{4}(I_N-I_{N+1})=\frac{\pi^2 I_N}{8(N+1)}JN<π24∫0π/2sin2xcos2Nxdx=π24(IN−IN+1)=π2IN8(N+1)
也即
0<\frac{4^N N!^2}{(2N)!}J_N<\frac{\pi^3}{16(N+1)}0<4NN!2(2N)!JN<π316(N+1)
证明18:Fejér核的证明
(Stark在1969年American Mathematical Monthly上的证明)
对于Fejér核有如下等式:
\left(\frac{\sin{nx/2}}{\sin{x/2}}\right)^2=\sum_{k=-n}^n(n-|k|)e^{ikx}=n+2\sum_{k=1}^n(n-k)\cos{kx}(sinnx/2sinx/2)2=∑k=−nn(n−|k|)eikx=n+2∑k=1n(n−k)coskx
故而有
\begin{align*} \int_0^\pi x\left(\frac{\sin{nx/2}}{\sin{x/2}}\right)^2 &= \frac{n\pi^2}{2}+2\sum_{k=1}^n(n-k)\int_0^\pi x\cos{kx}dx \\ &=\frac{n\pi^2}{2}-2\sum_{k=1}^n(n-k)\frac{1-(-1)^k}{k^2}\\ &=\frac{n\pi^2}{2}-4n\sum_{1\le k\le n,2\nmid k}\frac{1}{k^2}+4\sum_{1\le k\le n,2\nmid k}\frac{1}{k} \end{align*}∫0πx(sinnx/2sinx/2)2=nπ22+2∑k=1n(n−k)∫0πxcoskxdx=nπ22−2∑k=1n(n−k)1−(−1)kk2=nπ22−4n∑1≤k≤n,2∤k1k2+4∑1≤k≤n,2∤k1k
如果我们令n=2N,N\in\mathbb{Z^+}n=2N,N∈Z+,那么
\int_0^\pi \frac{x}{8N}\left(\frac{\sin{Nx}}{\sin{x/2}}\right)^2dx=\frac{\pi^2}{8}-\sum_{r=0}^{N-1}\frac{1}{(2r+1)^2}+O\left(\frac{\log{N}}{N}\right)∫0πx8N(sinNxsinx/2)2dx=π28−∑r=0N−11(2r+1)2+O(logNN)
但是由于 


