2022年丘成桐女子数学竞赛
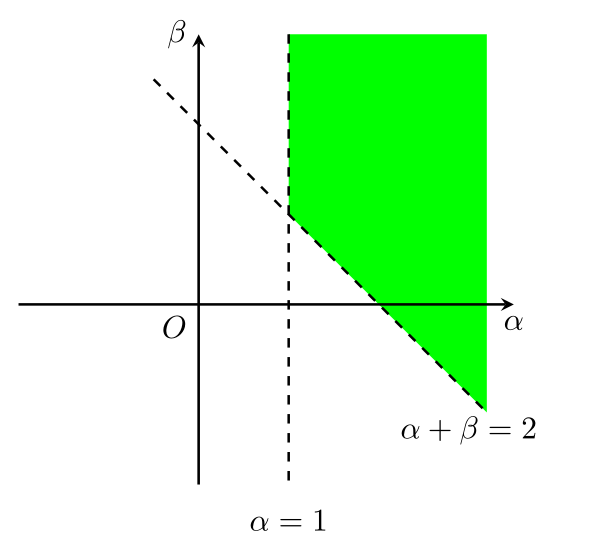
1. 求\alpha,\beta使得级数\sum\limits_{n=1}^{\infty}\sum\limits_{m=1}^n\dfrac{1}{n^{\alpha}m^{\beta}}收敛.
解答: 当\alpha\le 1时, 根据
\sum\limits_{m=1}^n\dfrac{1}{n^{\alpha}m^{\beta}} \ge \dfrac{1}{n^{\alpha}}, \\
于是原级数发散. 下设\alpha>1.
(1)当\beta\ge 0时, 由于
\int_{m}^{m+1}\dfrac{1}{x^{\beta}}\mathrm{d}x \le \dfrac{1}{m^{\beta}} \le \int_{m-1}^m\dfrac{1}{x^{\beta}}\mathrm{d}x, \\
所以
\int_1^{n}\dfrac{1}{x^{\beta}}\mathrm{d}x < \sum\limits_{m=1}^n\int_{m}^{m+1}\dfrac{1}{x^{\beta}}\mathrm{d}x \le \sum\limits_{m=1}^n\dfrac{1}{m^{\beta}} \le 1+ \sum\limits_{m=2}^n\int_{m-1}^m\dfrac{1}{x^{\beta}}\mathrm{d}x < 1+ \int_{1}^n\dfrac{1}{x^{\beta}}\mathrm{d}x,\\
(i)当\beta=1时, 上式变成
\ln n < \sum\limits_{m=1}^n\dfrac{1}{m} < 1+\ln n, \qquad \Rightarrow \qquad \dfrac{\ln n}{n^{\alpha}} < \sum\limits_{m=1}^n\dfrac{1}{n^{\alpha}m} < \dfrac{1+\ln n}{n^{\alpha}}.\\
所以当\alpha>1时, 原级数收敛; 当\alpha\le 1时, 原级数发散.
(ii)当\beta\ne 1时, 上式变成
\dfrac{1}{-\beta+1}(n^{-\beta+1}-1) \le \sum\limits_{m=1}^n\dfrac{1}{m^{\beta}} \le 1+\dfrac{1}{-\beta+1}(n^{-\beta+1}-1),\\
此时,
\dfrac{1}{-\beta+1}(n^{-\alpha-\beta+1}-n^{-\alpha}) \le \sum\limits_{m=1}^n\dfrac{1}{n^{\alpha}m^{\beta}} \le \dfrac{1}{n^{\alpha}}+\dfrac{1}{-\beta+1}(n^{-\alpha-\beta+1}-n^{-\alpha}).\\
当\alpha>1且\alpha+\beta-1>1(即\alpha+\beta>2)时, 原级数收敛; 其余情况发散.
(2)当\beta < 0时, 由于
\int_{m-1}^m\dfrac{1}{x^{\beta}}\mathrm{d}x < \dfrac{1}{m^{\beta}} < \int_{m}^{m+1}\dfrac{1}{x^{\beta}}\mathrm{d}x, \\
所以
1+\dfrac{1}{-\beta+1}(n^{-\beta+1}-1) = 1+ \int_{1}^n\dfrac{1}{x^{\beta}}\mathrm{d}x< \sum\limits_{m=1}^n\dfrac{1}{m^{\beta}} < \int_1^{n}\dfrac{1}{x^{\beta}}\mathrm{d}x = \dfrac{1}{-\beta+1}(n^{-\beta+1}-1),\\
此时,
\dfrac{1}{n^{\alpha}}+\dfrac{1}{-\beta+1}(n^{-\alpha-\beta+1}-n^{-\alpha})\le \sum\limits_{m=1}^n\dfrac{1}{n^{\alpha}m^{\beta}} \le \dfrac{1}{-\beta+1}(n^{-\alpha-\beta+1}-n^{-\alpha}) .\\
\alpha>1且\alpha+\beta-1>1(即\alpha+\beta>2)时, 原级数收敛; 其余情况发散.
2. 求椭圆C: \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1的内接六边形面积的最大值.
解答: 设椭圆C上六个点为P_i(\cos\theta_i,\sin\theta_i), i=1,2,3,4,5,6, 并且0<\theta_i<\theta_{i+1}. 内接六边形P_1P_2P_3P_4P_5P_6围成的区域记为\Omega. 为方便起见我们记\theta_7=\theta_1+2\pi, 那么P_7就是P_1.
(i)首先假设\Omega包含原点, 此时\theta_{i+1}-\theta_i < \pi. 于是\Omega的面积为
A(\Omega)=\dfrac{1}{2}\sum\limits_{i=1}^6\sin(\theta_{i+1}-\theta_i). \\
记\alpha_i=\theta_{i+1}-\theta_i, 则\alpha_1+\cdots+\alpha_6=\theta_7-\theta_1=2\pi, 由于\sin x在(0,\pi)上是凹函数, 所以根据Jensen不等式,
\dfrac{1}{6}\sum_{i=1}^6\sin\alpha_i \le \sin\left(\dfrac{1}{6}\sum_{i=1}^6\alpha_i\right)=\sin\dfrac{\pi}{3}=\dfrac{\sqrt{3}}{2}, \\
因此
A(\Omega)=\dfrac{1}{2}\sum_{i=1}^6\sin\alpha_i \le \dfrac{3\sqrt{3}}{2}. \\
等号成立条件是\alpha_1=\cdots=\alpha_6=\dfrac{\pi}{3}, 此时\Omega是边长为1的正六边形.
(ii)若\Omega不包含原点, 则圆C内部有一半与\Omega不相交, 于是A(\Omega) < \dfrac{\pi}{2} < \dfrac{3\sqrt{3}}{2}.
综上, A(\Omega)的最大值为\dfrac{3\sqrt{3}}{2}.
(2)对于一般的情况, 对单位圆x^2+y^2=1沿着两个坐标轴作伸缩变换即可得到椭圆C, 此时面积的最大值也会有相应的伸缩变换, 故A(\Omega)的最大值为\dfrac{3\sqrt{3}ab}{2}.
3. 设G按加法构成群, 满足G=\langle a,b\rangle, 其中a,b为生成元, 且12a+5b=0, 24a+16b=0.
(1)求a的阶的所有可能值.
(2)求群G在同构意义下的群结构.
解: 由条件, G的所有元素形如\{ma+nb|m,n\in\mathbb{Z}\}, 其中a,b\ne 0.
(1)由条件, 24a+10b=2(12a+5b)=0且24a+16b=0, 因此6b=0, 从而b可能是2,3,6阶的.
再由12a+5b=0可得12a-b=0并且72a+30b=0, 所以72a=0. 所以a可能是2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72阶的. 但12a=b\ne 0, 所以a不可能是2,3,4,6,12阶的, 于是只可能是8,9,18,24,36,72阶.
(i)若b是2阶的, 则由24a+16b=0可得24a=0, 所以a只可能是8,24阶的.
①当G=\mathbb{Z}/8\mathbb{Z}, b=4, a=1时, 满足12a+5b=32=0且24a+16b=0.
②当G=\mathbb{Z}/24\mathbb{Z}, b=12, a=1时, 满足12a+5b=72=0且24a+16b=24+192=0.
(ii)若b是3阶的, 则由12a-b=0可得36a-3b=0, 故36a=0, 所以a只可能是9,18,36阶的.
①当G=\mathbb{Z}/9\mathbb{Z}, b=3, a=1时, 满足12a+5b=27=0且24a+16b=72=0.
②当G=\mathbb{Z}/18\mathbb{Z}, b=6, a=5时, 满足12a+5b=90=0且24a+16b=120+96=216=0.
③当G=\mathbb{Z}/36\mathbb{Z}, b=12, a=1时, 满足12a+5b=72=0且24a+16b=24+192=216=0.
(iii)若b是6阶的, 则a只可能是8,9,18,24,36,72阶的.
当G=\mathbb{Z}/72\mathbb{Z}, b=12, a=1时, 满足12a+5b=72=0且24a+16b=24+192=216=0.
综上所述, a的阶的所有可能值是8,9,18,24,36,72.
(2)G中任意元素可以表示为ma+nb=ma+12na=(m+12n)a, 其中m,n\in\mathbb{Z}, 而m+12n可以表示任意整数, 所以G=\langle a\rangle. 由(1), a只可能是8,9,18,24,36,72阶, 所以根据循环群的定义, G在同构意义下只可能是8,9,18,24,36,72阶循环群, 即G只可能与\mathbb{Z}/k\mathbb{Z}(k=8,9,18,24,36,72)同构.
4. 在三维空间V中, 5个两两不同的二维空间两两相交为一维空间, 求交出的一维空间的个数的可能值.
(一定有更方便的做法)
结论1: 若三个二维空间相交得到的一维子空间有两个相同, 则三个一维子空间都相同, 即e_{ij}=e_{ik}能推出e_{ij}=e_{ik}=e_{jk}.
结论1证明: 设三个二维空间为V_i,V_j,V_k. 若e_{ij},e_{jk},e_{kl}有其中两个相同, 例如e_{ij}=e_{jk}, 则(V_i\cap V_j)\cup (V_i\cap V_k)=V_i\cup(V_j\cap V_k)=e_{ij}\supset e_{jk}, 所以必有e_{jk}=e_{ij}. \square
结论2: 若四个二维空间V_i,V_j,V_k,V_l中, V_i与V_j相交的一维子空间等于V_k与V_l相交的一维子空间, 则这四个二维子空间交出来的一维子空间都相同, 即e_{ij}=e_{kl}能推出e_{ij}=e_{jk}=e_{ik}=e_{il}=e_{jl}=e_{kl}.
结论2证明:设四个二维空间为V_i,V_j,V_k,V_l, 由条件, e_{ij}=V_i\cap V_j=V_k\cap V_l=e_{kl}, 但是
\begin{aligned} &\quad (V_j\cap V_k)\cup (V_i\cap V_k)\cup (V_j\cap V_l)\cup (V_i\cap V_l) \\ &=(V_k\cap(V_i\cup V_j)) \cup (V_l\cap(V_i\cup V_j)) \\ &=(V_i\cup V_j)\cap (V_k\cup V_l) = e_{ij}, \end{aligned}\\
所以e_{jk},e_{ik},e_{jl},e_{il}\subset e_{ij}, 从而必有e_{ij}=e_{jk}=e_{ik}=e_{il}=e_{jl}=e_{kl}. \square
证明: 假设二维空间为V_1,V_2,V_3,V_4,V_5, 并且记V_i\cap V_j=e_{ij}是V的一维子空间. 设S为交出的一维空间的个数.
首先, V_1,V_2,V_3之间交出的一维子空间: V_1\cap V_2=e_{12}, V_1\cap V_3=e_{13}, V_2\cap V_3=e_{23}.
(1)若e_{12},e_{13},e_{23}有其中两个相同, 由结论1可知e_{12}=e_{13}=e_{23}. 下面考虑e_{14},e_{24},e_{34}.
①若e_{14},e_{24},e_{34}至少有一个等于e_{12}=e_{13}=e_{23}, 例如e_{14}=e_{12}=e_{13}=e_{23}, 则根据结论1, e_{24}=e_{14}=e_{12}, 并且e_{34}=e_{14}=e_{13}. 于是这六个一维子空间都相同.
(a)若e_{15},e_{25},e_{35},e_{45}至少有一个等于e_{12}=e_{13}=e_{23}=e_{14}=e_{24}=e_{34}, 例如e_{15}等于上述六个一维子空间, 则根据结论1, e_{25}=e_{15}=e_{12}, e_{35}=e_{15}=e_{13}, e_{45}=e_{15}=e_{14}. 所以十个一维子空间都相同, 从而\boxed{S=1}.
(b)若e_{15},e_{25},e_{35},e_{45}都不等于e_{12}=e_{13}=e_{23}=e_{14}=e_{24}=e_{34}, 那么e_{15},e_{25},e_{35},e_{45}也两两不同(不然与结论1矛盾), 从而\boxed{S=5}.
②若e_{14},e_{24},e_{34}都不等于e_{12}=e_{13}=e_{23}, 则e_{14},e_{24},e_{34}两两不同(不然与结论1矛盾),
- (a)若e_{15},e_{25},e_{35}中至少有一个等于e_{12}=e_{13}=e_{23}, 则根据结论1, e_{25}=e_{15}=e_{12}且e_{35}=e_{15}=e_{13}, 即这六个一维子空间相同.
- (a-i)当e_{45}等于e_{12}=e_{13}=e_{23}=e_{15}=e_{25}=e_{35}时, 由结论2, e_{45}=e_{14}=e_{24}=e_{34}, 此时\boxed{S=1}.
- (a-ii)当e_{45}不等于e_{12}=e_{13}=e_{23}=e_{15}=e_{25}=e_{35}时, 也不可能等于e_{14},e_{24},e_{34}之一(不然与结论1矛盾), 此时\boxed{S=5}.
- (b)若e_{15},e_{25},e_{35}中至少有一个等于e_{14}或e_{24}或e_{34}且不等于e_{12}=e_{13}=e_{23}, 根据结论1可知e_{15},e_{25},e_{35}两两不同.
- (b-i)当存在i\in\{1,2,3\}满足e_{i5}=e_{i4}时, 不妨设e_{15}=e_{14}, 则由结论1可知e_{15}=e_{14}=e_{45}. 不可能有两个不同的i,j\in\{1,2,3\}满足e_{i5}=e_{i4}且e_{j5}=e_{j4}, 不然与“e_{15},e_{25},e_{35}两两不同”矛盾. 所以此时不同的一维子空间包括e_{12}=e_{13}=e_{23}, e_{24}, e_{34}, e_{15}=e_{14}=e_{45}, e_{35}, e_{25}, 因此\boxed{S=6}.
- (b-ii)当存在不同的i,j\in\{1,2,3\}满足e_{i5}=e_{j4}时, 不妨设e_{15}=e_{24}, 则根据结论2, e_{15}=e_{24}=e_{12}=e_{14}=e_{25}=e_{45}, 与“e_{14},e_{24},e_{34}两两不同”矛盾.
- (b-iii)当e_{15},e_{25},e_{35}与e_{14},e_{24},e_{34}之间都不相同, 则e_{45}也与这些一维子空间不相同(否则由结论2可推出矛盾), 则\boxed{S=8}.
(2)若e_{12},e_{13},e_{23}两两不同,
①若e_{14},e_{24},e_{34}有两个相同(不可能三个相同, 与结论1矛盾), 不妨设e_{14}=e_{24}=e_{12}(结论1).
- (a)若e_{15},e_{25},e_{35},e_{45}有两个相同(不可能至少三个相同, 与结论1矛盾):
- (a-i)当e_{15}=e_{25}或e_{15}=e_{45}或e_{25}=e_{45}时(只考虑第一种), 根据结论1和结论2有e_{12}=e_{14}=e_{24}=e_{15}=e_{25}=e_{45}, 所以\boxed{S=5}.
- (a-ii)当e_{15}=e_{35}或e_{25}=e_{35}时(只考虑第一种), e_{15}=e_{35}=e_{13}, 所以\boxed{S=6}.
- (a-iii)当e_{35}=e_{45}时, e_{35}=e_{45}=e_{34}, 所以\boxed{S=6}.
- (b)若e_{15},e_{25},e_{35},e_{45}两两不同, 则\boxed{S=8}.
②若e_{14},e_{24},e_{34}也两两不同并且不等于e_{12},e_{13},e_{23}(不然与结论1矛盾).
- (a)若e_{15},e_{25},e_{35},e_{45}有两个相同(不可能至少三个相同, 与结论1矛盾):
- (a-i)当e_{15}=e_{25}或e_{15}=e_{35}或e_{25}=e_{35}时(只考虑第一种), e_{15}=e_{25}=e_{45}, 此时\boxed{S=8}.
- (a-ii)当e_{15}=e_{45}或e_{25}=e_{45}或e_{35}=e_{45}时(只考虑第一种), e_{15}=e_{45}=e_{25}, 此时\boxed{S=8}.
- (b)若e_{15},e_{25},e_{35},e_{45}两两不同, 此时也不会与e_{12},e_{13},e_{23},e_{14},e_{24},e_{34}相同, 此时\boxed{S=10}.
综上, 所有不同的一维子空间个数的可能值为1,5,6,8,10.
5. 在平面直角坐标系中,
(1)三个整点组成的三角形的面积最小值为多少?
(2)半径为R的圆上一段长为R^{\frac{1}{3}}的圆弧上三点的面积最大为多少?
(3)在(2)中这段圆弧上至多有几个整点?
注: 某回忆版的(2)包括“圆心在原点”的条件, 我认为这条件是多余的, 加了这个条件之后(3)问是平凡的, 故去掉了.
(1)不妨设其中一个点是原点, 另外两个点为(a_1,b_1)与(a_2,b_2). 则面积为
\dfrac{1}{2}\left|\det\begin{bmatrix}a_1 & b_1 \\ a_2 & b_2\end{bmatrix}\right|=\dfrac{1}{2}|a_2b_1-a_1b_2|. \\
由于a_1,b_1,a_2,b_2都是整数, 所以|a_2b_1-a_1b_2|\ge 1, 等号成立的一个条件是a_1=1,b_1=0,a_2=0,b_2=1, 此时三角形面积为\dfrac{1}{2}. 所以三个整点组成的三角形的面积最小值为\dfrac{1}{2}.
(2)设长为R^{\frac{1}{3}}的圆弧的圆心角为\theta, 则
2\pi R\dfrac{\theta}{2\pi}=R^{\frac{1}{3}}, \\
故\theta=R^{-\frac{2}{3}}.
①当\theta \ge \dfrac{4\pi}{3}即R\le\left(\dfrac{3}{4\pi}\right)^{\frac{3}{2}}时, 面积最大值为\sqrt{3}, 此时三个顶点构成等边三角形.
②当\theta < \dfrac{4\pi}{3}即R>\left(\dfrac{3}{4\pi}\right)^{\frac{3}{2}}时, 面积最大值在两个顶点为圆弧端点、一个顶点为圆弧中点取到, 此时面积的最大值为
\begin{aligned} A&=\dfrac{1}{2}R^2\left[\sin\dfrac{\theta}{2}+\sin\dfrac{\theta}{2}-\sin\theta\right] \\ &=\dfrac{1}{2}R^2\left[2\sin\dfrac{R^{-\frac{2}{3}}}{2}-\sin(R^{-\frac{2}{3}})\right]. \end{aligned}\\
(3)由于R>0, 所以根据不等式x-\dfrac{x^3}{6}\le \sin x\le x(x\ge 0), 可知
A \le \dfrac{1}{2}R^2\left[R^{-\frac{2}{3}} - \left(R^{-\frac{2}{3}}-\dfrac{R^{-2}}{6}\right)\right] =\dfrac{1}{12} < \dfrac{1}{2},\\
所以根据(1)可知这段圆弧上不可能有3个整点.
下面构造有2个整点的例子: 考虑圆心为\left(\dfrac{1}{2},y_0\right)(y_0>0)且经过(0,0)和(1,0)的圆, 则半径R=\sqrt{\dfrac{1}{4}+y_0^2}, 过两点(0,0)和(1,0)的圆弧的圆心角为\alpha=2\arctan\dfrac{1}{2y_0}, 弧长可以写成y_0的函数:
l(y_0)=\alpha R=2R\arctan\dfrac{1}{2y_0}=\sqrt{1+4y_0^2}\arctan\dfrac{1}{2y_0}. \\
所以\lim\limits_{y_0\to+\infty}l(y_0)=1. 取y_0充分大使得
l(y_0)=\alpha R<\theta=R^{\frac{1}{3}}, \\
于是此时在经过(0,0),(1,0)且弧长为R^{\frac{1}{3}}的圆弧上存在两个整点.
6. n阶矩阵的所有元素均为\pm 1, 求所有此类矩阵的行列式的平均值.
解: 假设A是一个n阶矩阵, 定义\tilde{A}为把A的第一行的1换成-1、-1换成1得到的n阶矩阵, 相当于把A的第一行全都取相反数. 则根据行列式的运算法则, \det(\tilde{A})=-\det A, 即\det(\tilde{A})+\det A=0.
下面固定n阶矩阵的第2\sim n行. 由于第1行有2^n种不同的情况, 所以一共有2^n个不同的矩阵, 把这些矩阵的全体记为\mathscr{A}. 对任意的A\in\mathscr{A}, 都有\tilde{A}\in\mathscr{A}且满足\det(\tilde{A})+\det A=0. 所以\mathscr{A}中所有矩阵的行列式之和为0, 并且跟2\sim n行的元素选取无关.
因此, 此类矩阵的行列式之和都为0, 平均值也为0.
如何评价某大学 2022 年数学分析 C 期中考试试卷?
18 个回答
我给一下我知道的关于第三题反例的构造,相对而言比较复杂
我们记 \left\{ a_k\right\}=3^{k^4} , \left\{ c_r\right\}=\displaystyle\frac1{r^2},r\geq 1 ,并且分割区间 (0,\pi] 为 I_k=[\displaystyle\frac {\pi}{a_n},\frac{\pi}{a_{n-1}}]
定义函数 f(x)=\begin{cases} c_k\sin(a_kx),&x\in I_k=\displaystyle[\frac{\pi}{a_{k}},\frac{\pi}{a_{k-1}}]\\ 0 &x=0 \end{cases}
容易验证函数 f 在 [0,\pi] 上连续,我们接下来定义函数
g(x)=\begin{cases} \displaystyle\frac{f(x)}x&x\in(0,\pi]\\ 0& x=0 \end{cases}
那么 g(x) 实际上就是我们要求的反例.
首先来验证 g(x) 在 [0,\pi] 上的瑕积分存在.
注意到 \begin{align*} |\int_{I_k}g(x)\mathrm{d}x|=c_k|\int_{I_k}\frac{\sin(a_kx)}x\mathrm{d}x|=c_k|\int_{\pi}^{\pi\frac{a_k}{a_{k-1}}}\frac{\sin u}u\mathrm{d}u| \end{align*}
另一方面,由我们已经知道的经典结果 (\mathrm{Dirchlet} 积分) \displaystyle\int_0^{\infty}\frac{\sin x}x\mathrm{d}x=\frac{\pi}2 可知
\displaystyle c_k|\int_{\pi}^{\pi\frac{a_k}{a_{k-1}}}\frac{\sin u}u\mathrm{d}u|\leq c_kK ,其中 K 为常数.
故而有 \displaystyle\sum_{k=1}^{\infty}|\int_{I_k}g(x)\mathrm{d}x|\leq K\sum_{k=1}^{\infty}c_k=K\frac{\pi^2}6<+\infty
因而 \displaystyle\sum_{k=1}^{\infty}\int_{I_k}g(x)\mathrm{d}x<+\infty
而 \forall\delta\in(0,\pi) ,必然会落在一个 I_k 之中,因而有
\begin{align*} \int_{\delta}^{\pi}g(x)\mathrm{d}x&=c_k\int_{\delta}^{\frac{\pi}{a_{k-1}}}\frac{\sin(a_k x)}x\mathrm{d}x+\sum_{n=1}^{k-1}c_n\int_{\frac{\pi}{a_n}}^{\frac{\pi}{a_{n-1}}}\frac{\sin(a_nx)}x\mathrm{d}x\\ &=c_k\int_{I_k}\frac{\sin(a_kx)}{x}\mathrm{d}x-c_k\int_{\frac\pi{a_k}}^{\delta}\frac{\sin(a_kx)}x\mathrm{d}x+\sum_{n=1}^{k-1}c_n\int_{I_n}\frac{\sin(a_nx)}x\mathrm{d}x\\ &=\sum_{n=1}^kc_n\int_{\pi}^{\pi\frac{a_n}{a_{n-1}}}\frac{\sin u}u\mathrm{d}u-c_k\int_{\pi}^{a_k\delta}\frac{\sin u}u\mathrm{d}u \end{align*}
又 \forall \varepsilon>0,\exists N,k\geq N,c_k<\displaystyle\frac{\varepsilon}{2K}
并根据 \mathrm{Cauchy} 收敛定理,我们知 \exists M, 当 k\geq M 时有
|\displaystyle\sum_{k=M}^{\infty}\int_{I_k}g(x)\mathrm{d}x|<\frac{\varepsilon}2
此时记 H=\max\{M,N\} ,对于 0<\delta<\displaystyle\frac{\pi}{a_{H-1}}\Rightarrow\frac{\pi}{a_k}\leq\delta<\frac{\pi}{a_{k-1}},k\geq H
那么
\begin{align*} \quad\quad&|\int_\delta^\pi g(x)\mathrm{d}x-\sum_{k=1}^\infty\int_{I_k}g(x)\mathrm{d}x|\\ =&|\sum_{n=1}^k\int_{I_n}g(x)\mathrm{d}x-\int_{\frac{\pi}{a_k}}^{\delta}g(x)\mathrm{d}x-\sum_{k=1}^\infty\int_{I_k}g(x)\mathrm{d}x|\\ =&|-\int_{\frac{\pi}{a_k}}^{\delta}g(x)\mathrm{d}x-\sum_{n=k+1}^\infty\int_{I_n}g(x)\mathrm{d}x|\\ \leq&c_kK+\frac\varepsilon2<\varepsilon \end{align*}
进而推出 \displaystyle\int_0^\pi g(x)\mathrm{d}x=\displaystyle\sum_{k=1}^{\infty}\int_{I_k}g(x)\mathrm{d}x<+\infty ,即证的瑕积分的存在性.
现在来验证 g 并不绝对可积.
注意到 \displaystyle\int_{I_k}|g(x)|\mathrm{d}x=c_k\int_{I_k}\frac{|\sin(a_kx)|}x\mathrm{d}x=c_k\int_{\pi}^{\pi\frac{a_k}{a_{k-1}}}\frac{|\sin u|}u\mathrm{d}u
而
\begin{align*} \end{align*} \begin{align*} \int_{\pi}^{\pi\frac{a_k}{a_{k-1}}}\frac{|\sin u|}u\mathrm{d}u&=\sum_{n=1}^{3^{{k^4-(k-1)^4}}-1}\int_{n\pi}^{(n+1)\pi}\frac{|\sin u|}{u}\mathrm{d}u\\ &\geq\sum_{n=1}^{3^{{k^4-(k-1)^4}}-1}\frac1{(n+1)\pi}\int_{n\pi}^{(n+1)\pi}| \sin u|\mathrm{d}u\\ &=\sum_{n=1}^{3^{{k^4-(k-1)^4}}-1}\frac2{(n+1)\pi}\\ &\geq\frac2{\pi}(\ln(3^{k^4-(k-1)^4})-1)\\ &\geq\frac2\pi k^3\ln 3 \end{align*}
所以 \displaystyle \int_{I_k}|g(x)|\mathrm{d}x>\frac2\pi k\ln3 ,所以显然有不绝对可积.
最后来证明其为我们所求的反例.
注意到 \displaystyle\int_0^\pi g(t)\sin(nt)\mathrm{d}t=\int_0^\pi f(t)\frac{\sin(nt)}t\mathrm{d}t
命 J_k=\displaystyle\int_0^\pi f(t)\frac{\sin(a_kt)}t\mathrm{d}t ,我们知道欲导出矛盾只需证明当 k\to\infty 时有 J_k\to\infty 即可
而
\displaystyle J_k=\int_0^{\pi/a_k}f(t)\frac{\sin(a_kt)}{t}\mathrm{d}t+\int_{\pi/a_k}^{a/a_{k-1}}f(t)\frac{\sin(a_kt)}{t}\mathrm{d}t+\int_{\pi/a_{k-1}}^\pi f(t)\frac{\sin(a_kt)}t\mathrm{d}t=J_1+J_2+J_3
则
\begin{align*} \displaystyle|J_1|&\leq\int_0^{\pi/a_k}|f(t)||\frac{\sin(a_kt)}t|\mathrm{d}t\\ &\leq a_k\max_{t\in[0,\frac\pi{a_k}]}|f(t)|\frac\pi{a_k}=c_{k+1}\pi<1 \end{align*}
\begin{align*} J_2&=\int_{I_k}f(t)\frac{\sin(a_tt)}{t}\mathrm{d}t=c_k\int_{I_k}\frac{\sin^2(a_kt)}{t}\mathrm{d}t\\ &=\frac{c_k}{2}\int_{I_k}\frac{1-\cos(2a_kt)}{t}\mathrm{d}t\\ &=\frac{\ln3}{2k^2}(k^4-(k-1)^4)-\frac{c_k}2\int_{I_k}\frac{\cos(2a_kt)}{t}\mathrm{d}t \end{align*}
根据积分的第二中值定理定理,我们有 \displaystyle \int_{I_k}\frac{\cos(2a_kt)}{t}=\frac{a_k}\pi\int_{\pi/a_k}^C\cos(2a_kt)\mathrm{d}t=\frac1{2\pi}[\sin(2a_kt)]|^{C}_{\pi/a_k}
其中 \displaystyle \frac{\pi}{a_k}<C<\frac\pi{a_{k-1}}
由此我们可以立刻得出当 k\to\infty,J_2\to+\infty
而对于 J_3 我们有当 k\geq2 时,
\begin{align*} J_3&=\int_{\pi/a_{k-1}}^\pi f(t)\frac{\sin(a_kt)}t\mathrm{d}t\\ &=\sum_{n=1}^{k-1}\int_{I_n}c_n\sin(a_nt)\frac{\sin(a_kt)}t\mathrm{d}t\\ &=\sum_{n=1}^{k-1}\frac{c_n}2\int_{I_n}\frac{\cos((a_n-a_k)t)-\cos((a_n+a_k)t)}t\mathrm{d}t \end{align*}
而 \begin{align*} \int_{I_n}\frac{\cos((a_k-a_n)t)}{t}\mathrm{d}t&=\int_{\pi/a_n}^{\frac1{a_k-a_n}}\frac{\cos((a_k-a_n)t)}{t}\mathrm{d}t+\int_{\frac1{a_k-a_n}}^{\pi/a_{n-1}}\frac{\cos((a_k-a_n)t)}{t}\mathrm{d}t \\ &=\int_{\frac{\pi(a_k-a_n}{a_n}}^1\frac{\cos u}{u}\mathrm{d}u+\int^{\frac{\pi(a_k-a_n}{a_{n-1}}}_1\frac{\cos u}{u}\mathrm{d}u\\ &=\int^{\frac{\pi(a_k-a_n}{a_{n-1}}}_1\frac{\cos u}{u}\mathrm{d}u -\int^{\frac{\pi(a_k-a_n}{a_{n}}}_1\frac{\cos u}{u}\mathrm{d}u \end{align*}
同理,我们有 \displaystyle\int_{I_n}\frac{\cos((a_k+a_n)t)}{t}\mathrm{d}t=\int^{\frac{\pi(a_k+a_n}{a_{n-1}}}_1\frac{\cos u}{u}\mathrm{d}u -\int^{\frac{\pi(a_k+a_n}{a_{n}}}_1\frac{\cos u}{u}\mathrm{d}u
又因为 k\geq2,n<k,\displaystyle\frac{a_n}{a_n-1}>\frac{a_k}{a_n}\geq3
那么有 \displaystyle,\frac{\pi(a_k+a_n)}{a_n}>1,\frac{\pi(a_k+a_n)}{a_{n-1}}>1,\frac{\pi(a_k-a_n)}{a_n}>1
并且有 \displaystyle\frac{\pi(a_k-a_n)}{a_{n-1}}>\frac{\pi(a_k-a_n)}{a_n}>1
另一方面 \displaystyle\int_1^\infty\frac{\cos u}u\mathrm{d}u 收敛,这意味着 \displaystyle\int_1^x\frac{\cos u}u\mathrm{d}u 有界,不妨记 \displaystyle\int_1^x\frac{\cos u}u\mathrm{d}u<U
故当 k>n 时,有
\displaystyle|\int_{I_n}\frac{\cos((a_n-a_k)t)-\cos((a_n+a_k)t)}t\mathrm{d}t|\leq 4U
这也就是说 \displaystyle|J_3|\leq\sum_{n=1}^{k-1}2c_nU<\frac{\pi^2}6<+\infty
综上,我们有 J_1,J_3 一致有界,而 k\to\infty 时,我们有 J_2\to+\infty
所以我们有 k\to\infty 时, J_k\to+\infty ,也就是说
\displaystyle\lim_{n\to\infty}\int_0^\pi g(t)\sin(nt)\mathrm{d}t=+\infty\neq0\\ 这正是我们所要证的
简单看了一下,没仔细做,不过出题风格很像我们学校某著名数学分析老师的风格。以下提到的定理、例题编号都是梅加强《数学分析》(第2版)中的内容. 如果我考试的话,首先先把会做的做了:
第1题,可以很容易想到梅加强《数学分析》书的例8.1.3(判断了 \displaystyle\sum\limits_{n=1}^{\infty}\dfrac{\sin nx}{n} 在 [0,2\pi] 的一致收敛性)
第2题,乍一看是用Leibniz判别法,但通项并不单调地趋于0,不能直接用,对通项需要做一定的处理,比如取相邻两项看看会发生什么情况,即考虑 \begin{aligned} &\quad \sum\limits_{n=1}^{\infty}(a_{2n-1}+a_{2n}) \\ &=\sum\limits_{n=1}^{\infty}\left(\dfrac{-1}{2n-1+2\sin(2n-1)}+\dfrac{1}{2n+2\sin(2n)}\right) \\ &=\sum\limits_{n=1}^{\infty}\dfrac{-1-\sin 2n+\sin(2n-1)}{(2n+2\sin 2n)(2n-1+2\sin(2n-1))} \end{aligned}
然后通项的绝对值小于 \dfrac{3}{(2n-2)(2n-4)}, 用比较判别法可知 \sum\limits_{n=1}^{\infty}|a_{2n-1}+a_{2n}| 收敛,进而 \sum\limits_{n=1}^{\infty}(a_{2n-1}+a_{2n}) 收敛,【再根据原数列趋于0可知原级数收敛】.
我们也可以用Cauchy准则来验证,用Cauchy准则会得到 \sum\limits_{k=n+1}^ma_k ,每相邻两项作上述处理;如果这里是奇数个 a_k 求和,那么会多出来一个 a_m 也很容易作相应处理.
第3题,Riemann-Lebesgue引理(见例6.2.2)把Riemann可积的条件改为内闭可积会产生反例,但举反例可能要想一定时间,我不熟悉,直接跳.
第4题,第一问只需要求各阶导数即可;第二问需要求极限 \sqrt[n]{\dfrac{(2n)!!}{(2n-1)!!}} ,我们可以证明它的极限是1,然后x=\pm 1 时通项不趋于0,不收敛.
第5题,盲猜要用Abel求和,跟下面这题解法应该差不多:
选做题第2个是我在前几天写的一个解答!用归纳法可以证明: \left(\dfrac{\sin x}{x}\right)^n 的Fourier变换只在 [-n,n] 中非零.
好,现在已经有50分了(如果都做对的话),看看时间,如果时间不够了(半小时以下)就去想想第三题的反例。如果时间还有半小时以上,那我的做题顺序是:
第9题,试试假设 \displaystyle I_n=\int_0^{\infty}\dfrac{x^n}{e^{\pi\sqrt{x}}-1}\mathrm{d}x ,然后找递推公式看看行不行。因为
\displaystyle \begin{aligned} I_n&=\int_0^{\infty}\dfrac{x^n}{e^{\pi\sqrt{x}}-1}\mathrm{d}x \\ &=\dfrac{2}{\pi^{2n}}\int_0^{\infty}\dfrac{t^{2n+1}}{e^{t}-1}\mathrm{d}t \qquad (t=\pi\sqrt{x})\\ &=\dfrac{2}{\pi^{2n}}\int_0^{\infty}\dfrac{t^{2n+1}e^{-t}}{1-e^{-t}}\mathrm{d}t \\ &=\dfrac{2}{\pi^{2n}}\sum\limits_{k=1}^{\infty}\int_0^{\infty}t^{2n+1}e^{-kt}\mathrm{d}t. \end{aligned}
所以相当于找 \displaystyle J_{n,k}=\int_0^{\infty}t^{2n+1}e^{-kt}\mathrm{d}t 与 J_{n-1,k} 的递推关系式,应该用两次分部积分就行了,可以证明它是 \pi^{2n} 的有理数倍,这样结合 I_0 是有理数即可证完. (具体没算)
60分万岁,其他不会,不看了!
顺便心疼考这份卷的同学们,这份卷确实很难!
最后,我认为考试本来就应该是要考察学生的学习情况,及格的标准是该拿到的分都拿到,而80分以上属于优秀,所以出两道10分的难题来卡一下就行了。但这份卷真正"该拿的分"也就占40分(1,2,4,5题),第8、9题也许熟悉方法的同学可以做出来,但其他题或多或少还是在短时间内相当难做出来的。要么就把考试时间延长为3个小时,不然在考场上出这么多难题真的是意义不大,不如留作平时的思考题。
简单说一下最后一道选做题。这道题目的背景来自于概率论中的卷积。很明显题目中有几处讹误。
给定 n 个独立同分布的 X_i \sim U(-1,1) ,考察它们的和 S_n=X_1 + X_2 + \cdots +X_n 的分布。我们知道 X_i 的特征函数 \varphi_{X_i} (t)= \frac{\sin t}{t} ,所以它们的和 \varphi_{S_n}(t) = \left( \frac{\sin t}{t} \right)^n . 现在利用反转公式,对它做Fourier逆变换可以得到 S_n 的概率密度函数:\displaystyle f_{S_n}(x) = \frac 1\pi \int_0^\infty \left( \frac{\sin t}{t} \right)^n \cos tx \, \mathrm{d}t .
那么自然这个函数的支撑集就是 [-n,n] , 这是和函数可能取到的所有值的集合。
这道题目是Durrett书上的习题3.3.6,在习题的最后,Durrett还称,这个函数在区间 (k,k+1) 上是多项式,感兴趣的同学可以考虑一下怎么证明。
闲得没事考虑再看看前面的题目。
压轴题是一个经典结论,看到这个形式就应该能想到。
\begin{aligned} \displaystyle \int_0^\infty \frac{s^{2022}}{\mathrm{e}^{\pi \sqrt{s}}-1}\,\mathrm{d}s &= 2\int_0^\infty \frac{x^{4045}}{\mathrm{e}^{\pi x}-1}\,\mathrm{d}x \\ &=2\int_0^{\infty} \left( x^{4045} \sum_{k=0}^{\infty} \mathrm{e}^{- \left( k + 1 \right) \pi x} \right) \,\mathrm{d}x \\&= 2\sum_{k=0}^{\infty} \int_0^{\infty} x^{4045} \mathrm{e}^{-(k+1) \pi x} \,\mathrm{d}x \\ &= 2\frac{(4045)!}{\pi^{4046}} \zeta(4046). \end{aligned}
所以接下来的问题变成如何证明 \frac{\zeta(4046)}{\pi^{4046}} 是有理数,事实上对于正偶数 2n ,我们有\zeta (2n)={\frac {(-1)^{n+1}B_{2n}(2\pi )^{2n}}{2(2n)!}}。如此自然证明了想要的结论。
第八题我盲猜是不存在。感觉形式和Ramanujan's Master Theorem有关系,但是不太清楚怎么证明。
再说一下第七题,这个老师是真的不当人……结论是蛮经典的结论:
给定某个二次有理方程的根 \alpha,则 F(\alpha) =\displaystyle\sum_{n=1}^\infty \frac{\cot(n\pi \alpha)}{n^3} 是收敛的,且能确切求出其值。
收敛是容易的,事实上 \sum_{n=1}^\infty\frac{1}{n^3 \sin \left( n \pi \alpha \right)} 也是收敛的,稍微做一点点必要的放缩能看出来 \sin(n\pi\alpha) \sim O(n) ,这样和 \zeta(2) 比较审敛就可以。
现在用留数定理计算它的值,考虑函数 f(z) = \frac{\cot(z\pi)\cot(z\pi \alpha)}{z^3} , z=n 和 \frac n\alpha 是 f 的一阶奇点( n\in \mathbb{Z} \backslash \{0 \} ), z=0 是 f 的五阶奇点。取矩形围道 \gamma_N ,顶点为 (\pm N , \pm Ni) ,记其所围区域为 \Gamma_N 。考虑利用留数定理:
\begin{aligned} \frac{1}{2\pi i} \int_{\gamma_N}f(z) \, \mathrm{d}z &= \operatorname{res}[f:0] + \sum_{n\in \Gamma_N, n\ne 0}\operatorname{res}[f:n] + \sum_{\frac{n}{\alpha}\in \Gamma_N, n\ne 0}\operatorname{res}\left[f:\frac{n}{\alpha}\right] \\ &= \frac{ \alpha^4-5 \alpha^2+1}{45 \alpha} \cdot\pi ^2\\ &\qquad+ \sum_{n\in \Gamma_N, n\ne 0}\frac{\cot(n\pi\alpha)}{\pi n^3} + \sum_{\frac{n}{\alpha}\in \Gamma_N, n\ne 0} \frac{\alpha^2\cot\frac{n\pi}{\alpha}}{\pi n^3}. \end{aligned}
为了利用留数定理,我们需要左边的围道积分趋于 0 ,因为 n\alpha \mod 1 是均匀分布的(Weyl判别法),我们能取一列 N_i \in \mathbb{N} 使得在 \gamma_{N_i + \frac{1}{4}} 和 \gamma_{N_i + \frac{3}{4}}之间的部分 f 的分子一致有界的。现在我们知道了 F(\alpha) + \alpha^2 F\left( \frac{1}{\alpha} \right) = \frac{\alpha^4 - 5\alpha^2 + 1}{90 \alpha} \cdot \pi^3 。以下解这个关于 \alpha 的方程即可,为此需要 \alpha 的连分式展开,反复迭代直到出现循环。
特别地,当 \alpha = \sqrt{61} 时,wolframalpha告诉我们 \alpha=\left [7; \overline{1, 4, 3, 1, 2, 2, 1, 3, 4, 1, 14} \right] ,代入计算即可,我也不知道算出来是多少,倒霉wolframalpha直接说它diverge了……
第六题的结论可以理解成当 f' 有界时绝对连续能得出Lipschitz连续,似乎是个classical的结论。
这样这个回答加上上面那个答主的,基本能解决所有题目了。
这份卷子可以给眼界开阔的同学用作练习
作为考试,应该算是命题事故。。。
整张卷子严格来说只有1、2、4、5、6、8是可做的,但是很多高手可能会误以为难度按题号递增,直接寄在第三题,这其实很不公平
第九题在众神必题中还算相对可做,但需要对伯努利数有比较深刻的了解,如果你刷过谢惠民的话这个题是有机会做出的
选做B也算相对可做,但是数学系的同学在这块更多的是研究dirichlet核和Hilbert 空间之类充满分析的东西,在卷积的运算和性质上还不如统计和信号系统的同学,所以除非面面俱到的超级大佬,在考场上做出还是相当困难的
第七题是喜闻乐见的无理测度问题,作为一个盛产open problem的领域,已经成为知乎钓鱼题的重灾区。这告诉大家奇怪的三角级数不要轻易尝试,更别提遇到这种一眼看上去数论味满满的sqrt61
看了一下,第八题还没有人写,我来简单写一下:
首先注意到 f(0)=0 ,于是
\sqrt{n}f(\frac{1}{n})=\sqrt{n}\sum_{k=0}^{\infty}{a_k(\frac{1}{n})^k}=\sqrt{n}\sum_{k=1}^{\infty}{a_k(\frac{1}{n})^k}\\=\frac{1}{\sqrt{n}}\sum_{k=1}^{\infty}{a_k(\frac{1}{n})^{k-1}}=\frac{1}{\sqrt{n}}\sum_{k=0}^{\infty}{a_{k+1}(\frac{1}{n})^{k}}\rightarrow0
最后一步是由于闭区间上的连续函数存在最大值
然而 \sqrt{n}f(\frac{1}{n})\rightarrow\sqrt{\pi} ,矛盾,所以不存在
尝试一下7题。

答:级数收敛,其和为 -\frac{16793\pi^3}{45660\sqrt{61}} 。
#经数学群大佬指点,这题要运用无理数的有理逼近,这样的话收敛性就是显然的了.不过需要的引理很不显然,来源于Roth在1955年得Fields奖的工作,不证,详见华罗庚《数论导引》p473/GTM201 p300。
证明1:
引理(Roth定理):对任意代数数 \alpha 和 \varepsilon>0 ,不等式: \left| \frac{p}{q}-\alpha \right|\le\frac{1}{q^{2+\varepsilon}}\\ 只有有限个有理解 \frac{p}{q}\in\mathbb{Q} ,等价表述为对于任意 \varepsilon>0 ,存在仅与 \alpha,\varepsilon 有关的常数 C(\alpha,\varepsilon)>0 ,使得对于所有 \frac{p}{q}\in\mathbb{Q} ,有不等式: \left| \frac{p}{q}-\alpha \right|\ge\frac{C(\alpha,\varepsilon)}{q^{2+\varepsilon}}\\ .
有了引理之后我们取 0<\varepsilon<1 ,可以发现: \sum\limits_{n=1}^{\infty}{\frac{\mathrm{cos}(\sqrt{61}n\pi)}{n^3\mathrm{sin}(\sqrt{61}n\pi)}}=\sum\limits_{n=1}^{\infty}{\frac{\mathrm{cos}(\sqrt{61}n\pi-m\pi)}{n^3\mathrm{sin}(\sqrt{61}n\pi-m\pi)}}\\<\sum\limits_{n=1}^{\infty}{\frac{\mathrm{cot}(n\pi\left| \sqrt{61}-\frac{m}{n} \right|)}{n^3}}\\<\sum\limits_{n=1}^{\infty}\frac{1}{n^4\pi\times\frac{C}{n^{2+\varepsilon}}}=\frac{1}{C\pi}\sum\limits_{n=1}^{\infty}\frac{1}{n^{2-\epsilon}}\\ 故级数收敛。
由于答主无数论基础,所以想出了证法2以供参考。
证明2:证明收敛前需证明以下等式:
\mathrm{cot}x=\frac{1}{x}+\sum_\limits{n=1}^{\infty}\frac{2x}{x^2-(n\pi)^2}\\
等式的证明:
对 \mathrm{cos}\,ax 在 [-\pi,\pi] 上的Fourier展开,我们有: \mathrm{cos}\,ax=\frac{\mathrm{sin}\,a\pi}{a\pi}+\frac{2a\,\mathrm{sin}\,a\pi}{\pi}\sum\limits_{n=1}^{\infty}\frac{(-1)^n\mathrm{cos}\,nx}{a^2-n^2}\\令 x=\pi ,得 \mathrm{cos}\,a\pi=\frac{\mathrm{sin}\,a\pi}{a\pi}+\frac{2a\,\mathrm{sin}\,a\pi}{\pi}\sum\limits_{n=1}^{\infty}\frac{1}{a^2-n^2}\\\Rightarrow\mathrm{cot}\,a\pi=\frac{1}{a\pi}+\sum_\limits{n=1}^{\infty}\frac{2a\pi}{(a\pi)^2-(n\pi)^2}\\ 等式证完后,代入 a=\sqrt{61}n ,得
\sum\limits_{n=1}^{\infty}{\frac{\mathrm{sin}(\sqrt{61}n\pi)}{n^3\mathrm{cos}(\sqrt{61}n\pi)}}=\sum\limits_{n=1}^{\infty}{\frac{1}{\sqrt{61}\pi n^4}}+\frac{2\sqrt{61}}{\pi}\sum\limits_{n=1}^{\infty}\sum\limits_{k=1}^{\infty}{\frac{1}{n^2(61n^2-k^2)}}\\ 等式右边第一项易知是有限的,下证第二项也是有限的,
由于 n,k 都是正整数,所以当 k>8n 时,级数为负, 0>\sum\limits_{n=1}^{\infty}\sum\limits_{k\geq 8n}^{\infty}{\frac{1}{n^2(61n^2-k^2)}}>-\frac{64}{3}\sum\limits_{n=1}^{\infty}\frac{1}{n^2}\sum\limits_{k=1}^{\infty}\frac{1}{k^2}=-\frac{64}{3}\zeta^2(2)\\ 当 k\leq 7n 时,级数为正 0<\sum\limits_{n=1}^{\infty}\sum\limits_{k=1}^{k\leq 7n}{\frac{1}{n^2(61n^2-k^2)}}<\frac{49}{12}\sum\limits_{n=1}^{\infty}\frac{1}{n^2}\sum\limits_{k=1}^{\infty}\frac{1}{k^2}=\frac{49}{12}\zeta^2(2)\\
当 7n<k<8n 时, 0<\sum\limits_{n=1}^{\infty}\sum\limits_{k>7n}^{k<8n}{\left| \frac{1}{n^2(61n^2-k^2)} \right|}<\sum\limits_{n=1}^{\infty}\frac{1}{12n^4}\sum\limits_{k>7n}^{k<8n}1<\frac{1}{12}\zeta(3)\\
所以可知原级数收敛。
不过关于这个级数求和目前还没有什么想法.也许由其他答主所言需要数学分析以外的工具。
二更:
对于求和问题,必须要用到复分析,且计算极其复杂。大佬贴出了一个链接(见下文),我就把结论贴出来吧。
\sum\limits_{n=1}^{\infty}\frac{\mathrm{cot}(\sqrt{61}n\pi)}{n^3}=-\frac{16793\pi^3}{45660\sqrt{61}}\\ 并且对于这种级数,我们有一般结论:
对于函数 F(\alpha)=\sum\limits_{n=1}^{\infty}\frac{\mathrm{cot}(n\pi\alpha)}{n^{2k+1}}\\ 其中 \alpha 为二次无理数,我们有 \frac{F(\alpha)}{\pi^{2k+1}}\in\mathbb{Q}(\alpha)\\ .
评价:看完整张卷子,要说其他题还能做的话,这一题就直接体现了出卷老师满满的恶趣味,很明显这一题就不想让学生拿分(乐),并且从这一题和第九题来看,这出卷老师十九八九是搞数论的。最后奉劝出卷老师一句话:老老实实出题,不要总想搞个大新闻哈哈!












【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 分享4款.NET开源、免费、实用的商城系统
· 全程不用写代码,我用AI程序员写了一个飞机大战
· MongoDB 8.0这个新功能碉堡了,比商业数据库还牛
· 白话解读 Dapr 1.15:你的「微服务管家」又秀新绝活了
· 上周热点回顾(2.24-3.2)