Formelsammlung Mathematik: Bestimmte Integrale: Form R(x,tan)

 

0.1Bearbeiten

{\displaystyle \int _{0}^{\pi }x\,\tan x\,dx=-\pi \,\log 2}

Beweis

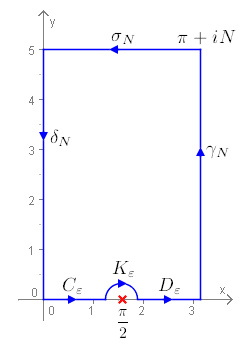
Setzt man {\displaystyle f(z)=z\,\tan z}, so ist

{\displaystyle \int _{C_{\varepsilon }}f\,dz+\int _{K_{\varepsilon }}f\,dz+\int _{D_{\varepsilon }}f\,dz+\int _{\gamma _{N}}f\,dz+\int _{\sigma _{N}}f\,dz+\int _{\delta _{N}}f\,dz=\oint f\,dz=0}.

Nun ist {\displaystyle \lim _{\varepsilon \to 0+}\int _{C_{\varepsilon }}f\,dz+\int _{D_{\varepsilon }}f\,dz={\text{p.V.}}\int _{0}^{\pi }x\,\tan x\,dx}

und {\displaystyle \lim _{\varepsilon \to 0+}\int _{K_{\varepsilon }}f\,dz=-i\pi \,{\text{res}}\left(f,{\frac {\pi }{2}}\right)={\frac {i\pi ^{2}}{2}}}.

Und aus {\displaystyle \int _{\gamma _{N}}f\,dz+\int _{\delta _{N}}f\,dz=\int _{0}^{N}f(\pi +iy)\,i\,dy-\int _{0}^{N}f(iy)\,i\,dy=-\pi \int _{0}^{N}\tanh y\,dy=-\pi \log(\cosh N)}

und {\displaystyle \int _{\sigma _{N}}f\,dz=-\int _{0}^{\pi }f(x+iN)\,dx=\pi \log(2\cosh N)-{\frac {i\pi ^{2}}{2}}}

folgt {\displaystyle \int _{\gamma _{N}}f\,dz+\int _{\sigma _{N}}f\,dz+\int _{\delta _{N}}f\,dz=\pi \log 2-{\frac {i\pi ^{2}}{2}}}.

Also ist {\displaystyle {\text{p.V.}}\int _{0}^{\pi }x\,\tan x\,dx+\pi \log 2=0}.

 

0.2Bearbeiten

{\displaystyle \int _{0}^{\frac {\pi }{4}}\log(1+\tan x)\,dx={\frac {\pi }{8}}\log 2}

Beweis

Wegen {\displaystyle 1+\tan x={\frac {\cos x+\sin x}{\cos x}}={\frac {{\sqrt {2}}\cos \left({\frac {\pi }{4}}-x\right)}{\cos x}}}

ist {\displaystyle \log(1+\tan x)={\frac {1}{2}}\log 2+\log \cos \left({\frac {\pi }{4}}-x\right)-\log(\cos x)}.

Da nach Substitution {\displaystyle x\mapsto {\frac {\pi }{4}}-x}

{\displaystyle \int _{0}^{\frac {\pi }{4}}\log \cos \left({\frac {\pi }{4}}-x\right)\,dx=\int _{0}^{\frac {\pi }{4}}\log(\cos x)\,dx} ist,

ist das gesuchte Integral {\displaystyle \int _{0}^{\frac {\pi }{4}}{\frac {1}{2}}\log 2\,dx={\frac {\pi }{8}}\,\log 2} .

 

1.1Bearbeiten

{\displaystyle \int _{-\infty }^{\infty }{\frac {\tan \alpha x}{x}}\,dx=\pi \qquad \alpha >0}

Beweis

Nach der Formel von Lobatschewski ist {\displaystyle \int _{-\infty }^{\infty }1\cdot {\frac {\tan x}{x}}\,dx=\int _{0}^{\pi }1\,dx=\pi }.

Substituiert man {\displaystyle x\to \alpha x\,}, so erhält man die behauptete Formel.

 

1.2Bearbeiten

{\displaystyle \int _{0}^{\frac {\pi }{2}}{\frac {1}{1+\tan ^{\alpha }x}}\,dx={\frac {\pi }{4}}\qquad \alpha \in \mathbb {C} \setminus i\mathbb {R} ^{\times }}

Beweis

Für {\displaystyle \alpha \in \mathbb {C} \setminus i\mathbb {R} ^{\times }} sei {\displaystyle I(\alpha )=\int _{0}^{\frac {\pi }{2}}{\frac {1}{1+\tan ^{\alpha }x}}\,dx}.

Nach Substitution {\displaystyle x\mapsto {\frac {\pi }{2}}-x} ist {\displaystyle I(\alpha )=\int _{0}^{\frac {\pi }{2}}{\frac {1}{1+\cot ^{\alpha }x}}\,dx=\int _{0}^{\frac {\pi }{2}}{\frac {\tan ^{\alpha }x}{1+\tan ^{\alpha }x}}\,dx}.

Addiert man die verschiedenen Darstellungen von {\displaystyle I(\alpha )\,}, so ist {\displaystyle 2I(\alpha )=\int _{0}^{\frac {\pi }{2}}{\frac {1+\tan ^{\alpha }x}{1+\tan ^{\alpha }x}}\,dx={\frac {\pi }{2}}}.

Unabhängig von {\displaystyle \alpha \,} gilt also {\displaystyle I(\alpha )={\frac {\pi }{4}}}.

 

1.3Bearbeiten

{\displaystyle \int _{0}^{\frac {\pi }{2}}\tan ^{2\alpha -1}\,x\;dx={\frac {\pi }{2\sin \alpha \pi }}\qquad 0<{\text{Re}}(\alpha )<1}

Beweis

Verwende die Formel

{\displaystyle 2\int _{0}^{\frac {\pi }{2}}\sin ^{2\alpha -1}x\,\cos ^{2\beta -1}x\,dx={\frac {\Gamma (\alpha )\,\Gamma (\beta )}{\Gamma (\alpha +\beta )}}\qquad {\text{Re}}(\alpha ),{\text{Re}}(\beta )>0}.

Ist {\displaystyle 0<{\text{Re}}(\alpha )<1\,} und setzt man {\displaystyle \beta =1-\alpha \,}, so ist auch {\displaystyle 0<{\text{Re}}(\beta )<1\,}.

Also ist {\displaystyle 2\int _{0}^{\frac {\pi }{2}}\tan ^{2\alpha -1}x\;dx=\Gamma (\alpha )\,\Gamma (1-\alpha )}.

Und das ist {\displaystyle {\frac {\pi }{\sin \alpha \pi }}} nach dem Eulerschen Ergänzungssatz.