平面几何问题

2.28  正三角形带电薄片（带正电荷）位于$\,\Sigma\colon\,x+y+z=-a$（其中$\,a>0$）的平面上，且带电薄片限定于$-a\le x\le 0$与$-a\le y\le 0$之间，
        其电荷面密度为$\sigma$，试求出原点处的电场强度$\boldsymbol{E}$（矢量）
$$\left|\overrightarrow{\boldsymbol{E}}\,\right|\,=\sqrt{3}\displaystyle\iint\limits_{\Sigma\colon\,x+y+z=-a}\dfrac{\sigma\,\,{\rm\,d}S}{4\pi\varepsilon_0\left(x^2+y^2+z^2\right)}\dfrac{\left|x\right|}{\sqrt{x^2+y^2+z^2}}$$

$$\big|\overrightarrow{\boldsymbol{E}}\big|\,\cos\langle\overrightarrow{\boldsymbol{E}},\overrightarrow{\boldsymbol{i}}\rangle=\displaystyle\iint\limits_{\Sigma\colon\,x+y+z=-a}\dfrac{\sigma\,\left|x\right|\,{\rm\,d}S}{4\pi\varepsilon_0\left(x^2+y^2+z^2\right)^{\frac{3}{2}}}$$
$$\big|\overrightarrow{\boldsymbol{E}}\big|\,\cos\langle\overrightarrow{\boldsymbol{E}},\overrightarrow{\boldsymbol{j}}\rangle=\displaystyle\iint\limits_{\Sigma\colon\,x+y+z=-a}\dfrac{\sigma\,\left|y\right|\,{\rm\,d}S}{4\pi\varepsilon_0\left(x^2+y^2+z^2\right)^{\frac{3}{2}}}$$
$$\big|\overrightarrow{\boldsymbol{E}}\big|\,\cos\langle\overrightarrow{\boldsymbol{E}},\overrightarrow{\boldsymbol{k}}\rangle=\displaystyle\iint\limits_{\Sigma\colon\,x+y+z=-a}\dfrac{\sigma\,\left|z\right|\,{\rm\,d}S}{4\pi\varepsilon_0\left(x^2+y^2+z^2\right)^{\frac{3}{2}}}$$

$$\begin{align*}   \big|\overrightarrow{\boldsymbol{E}}\big|\,&=\sqrt{3}\displaystyle\iint\limits_{\Sigma\colon\,x+y+z=-a}\dfrac{\sigma\,\left|x\right|\,{\rm\,d}S}{4\pi\varepsilon_0\left(x^2+y^2+z^2\right)^{\frac{3}{2}}}\\   &=\frac{\sqrt{3}\,\sigma}{4\pi\varepsilon_0}  \displaystyle\iint\limits_{\Sigma\colon\,x+y+z=-a}\dfrac{\,\left|x\right|\,}{\left(x^2+y^2+z^2\right)^{\frac{3}{2}}}{\rm\,d}S\\  &=\frac{\sqrt{3}\,\sigma}{4\pi\varepsilon_0}  \int_{-a}^0\int_{-a-y}^0 \dfrac{\sqrt{3}\,\left|x\right|}{\left(x^2+y^2+\left(-a-x-y\right)^2\right)^{\frac{3}{2}}}{\rm\,d}x{\rm\,d}y\\ &=\frac{\sqrt{3}\,\sigma}{4\pi\varepsilon_0}  \int_{-a}^0\int_{-a-y}^0 \dfrac{\sqrt{3}\,\left|x\right|}{\left(x^2+y^2+\left(a+x+y\right)^2\right)^{\frac{3}{2}}}{\rm\,d}x{\rm\,d}y\\  &=\frac{\sqrt{3}\,\sigma}{4\pi\varepsilon_0}  \int_0^a\int_0^{a-y} \dfrac{\sqrt{3}\,x}{\left(x^2+y^2+\left(a-x-y\right)^2\right)^{\frac{3}{2}}}{\rm\,d}x{\rm\,d}y\\ &=\frac{3\,\sigma}{4\pi\varepsilon_0}  \int_0^a\int_0^{a-y} \dfrac{\,x}{\left(x^2+y^2+\left(a-x-y\right)^2\right)^{\frac{3}{2}}}{\rm\,d}x{\rm\,d}y\\  \end{align*}$$

$$\begin{align*}  \color{red}{\boxed{\quad\color{black}{\int_0^a\int_0^{a-y} \dfrac{\,x}{\left(x^2+y^2+\left(a-x-y\right)^2\right)^{\frac{3}{2}}}{\rm\,d}x{\rm\,d}y\,=\,\frac{\pi}{6}}\quad}}  \end{align*}$$

 

如图,分别以$\triangle ABC$的边$AC,BC$为一边在三角形外作正方形$ACFG$和$BCED$, $I$为$EF$上的中点,求证: $IH\perp AB$.

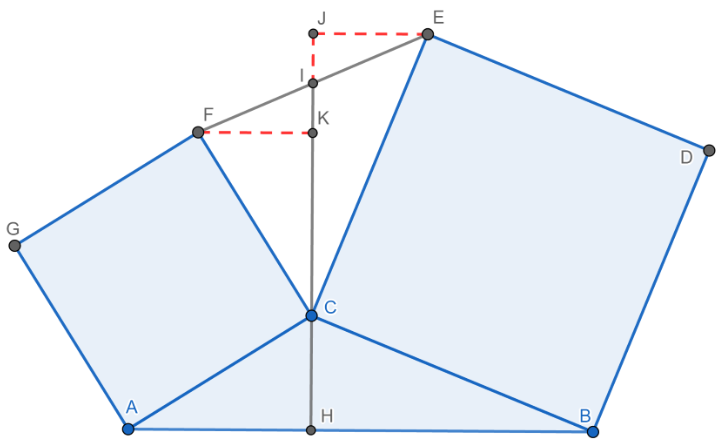
如图,分别以$\triangle ABC$的边$AC,BC$为一边在三角形外作正方形$ACFG$和$BCED$, $IH\perp AB$,求证: $I$为$EF$上的中点.

过$EJ$作$CF$的平行线交$CI$的延长线于$J$.证明$\triangle CEJ\cong ACB$,则$EJ=CB=FC$,从而四边形$EJFC$为平行四边形,那么$M$为$FH$上的中点.

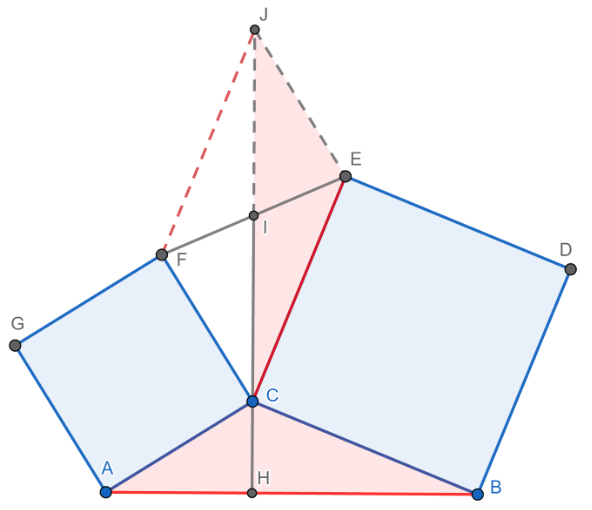
分别过$E,F$作$CI$的垂线,垂足为$J,K$.

---

\documentclass[11pt,no-math,a4paper]{article}
\RequirePackage{xeCJK}

%%%修改数学字体
\usepackage{fontspec}
\usepackage[T1]{fontenc}
\usepackage{times}
\usepackage[complete,amssymbols,amsbb,eufrak,nofontinfo,
subscriptcorrection,zswash,mtpscr]{mtpro2}

%\usepackage{mathpazo}
%\renewcommand{\rmdefault}{ibh}
%\usepackage{fourier}
%\usepackage{charter}
%\usepackage{helvet}
\usepackage{amsmath,amsthm}
\allowdisplaybreaks[4]
%%%修改数学字体
%\usepackage{CJKnumb}
%\usepackage{amsmath,amssymb,amsthm}

\setCJKmainfont[BoldFont={方正黑体简体},ItalicFont={方正楷体简体}]{方正书宋简体}
%\setCJKsansfont[BoldFont={黑体}]{方正中等线简体}
%\setCJKmonofont{方正中等线简体}

\setCJKfamilyfont{kd}{华文行楷}
\setmainfont{Times New Roman}
\setsansfont{DejaVu Sans}
\setmonofont{Latin Modern Mono}

\setCJKfamilyfont{song}{方正书宋简体}
\newcommand{\song}{\CJKfamily{song}}
\setCJKfamilyfont{hei}{方正黑体简体}
\newcommand{\hei}{\CJKfamily{hei}}
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

\newcommand{\chaoda}{\fontsize{55pt}{\baselineskip}\selectfont}
\newcommand{\chuhao}{\fontsize{42pt}{\baselineskip}\selectfont} % 字号设置
\newcommand{\xiaochuhao}{\fontsize{36pt}{\baselineskip}\selectfont} % 字号设置
\newcommand{\yihao}{\fontsize{28pt}{\baselineskip}\selectfont} % 字号设置
\newcommand{\erhao}{\fontsize{21pt}{\baselineskip}\selectfont} % 字号设置
\newcommand{\xiaoerhao}{\fontsize{18pt}{\baselineskip}\selectfont} % 字号设置
\newcommand{\sanhao}{\fontsize{15.75pt}{\baselineskip}\selectfont} % 字号设置
\newcommand{\xiaosanhao}{\fontsize{15pt}{\baselineskip}\selectfont} % 字号设置
\newcommand{\sihao}{\fontsize{14pt}{\baselineskip}\selectfont} % 字号设置
\newcommand{\xiaosihao}{\fontsize{12pt}{14pt}\selectfont} % 字号设置
\newcommand{\wuhao}{\fontsize{10.5pt}{12.6pt}\selectfont} % 字号设置
\newcommand{\xiaowuhao}{\fontsize{9pt}{11pt}{\baselineskip}\selectfont} % 字号设置
\newcommand{\liuhao}{\fontsize{7.875pt}{\baselineskip}\selectfont} % 字号设置
\newcommand{\qihao}{\fontsize{5.25pt}{\baselineskip}\selectfont} % 字号设置

 

 

 

\usepackage{tikz}
\usepackage{makeidx}
\usepackage{enumitem}
%\usepackage[left=2.6cm,right=2.6cm,top=2.54cm,bottom=2.54cm]{geometry}
\usepackage[body={16cm,26.67cm}, left=0.6cm,right=0.6cm,top=0.54cm,bottom=0.54cm]{geometry}
%\geometry{papersize={480mm,800mm}}
%\usepackage{mathtools}
%\usepackage{mathrsfs}

\usepackage{multirow,booktabs}
\usepackage{makecell}
%\title{中国科学技术大学\\
%2015年硕士学位研究生入学考试试题}
%\author{(线性代数与解析几何)}
%\date{}

%\newenvironment{newproof}{\par\CJKfamily{xiao}\noindent{\makebox[0pt][r]{\;\;}\textbf{证明:}}\color{black!90}\small}{\hfill$\Box$\quad\par}

%\newenvironment{solution}{\par\CJKfamily{xiao}\noindent{\makebox[0pt][r]{\;\;}\textbf{解:}}\small}{\hfill$\Box$\quad\par}

\newenvironment{Proof}{\par\noindent{\hei 证明}\hspace{1em}}{\qed\par}
\newenvironment{Answer}{\par\noindent{\hei 答}\hspace{1em}}{\par\song}
\newenvironment{Solution}{\par\noindent{\hei 解}\hspace{1em}}{\hfill$\lhd$\par\vspace{6pt}\song}
\newcommand{\Ker}{\mathrm{Ker}\,}

\usepackage{fancyhdr}
\usepackage{fancybox}
\usepackage{lastpage}%此宏包是获取总页数用的。
\pagestyle{fancy}
\renewcommand{\headrulewidth}{0pt}%设置页眉线
\renewcommand{\footrulewidth}{1pt}%设置页脚线

\fancyhf{}%清除所有页眉页脚

\lfoot{科目名称：数学}
\cfoot{}
\rfoot{第\thepage 页\quad 共\pageref{LastPage} 页}

\usepackage{shadethm}
\newshadetheorem{theorem}{}%[section]
%\shadetheoremstyle{plain}

\begin{document}
%\maketitle

%\fancypage{%
%\setlength{\fboxsep}{13pt}%
%\setlength{\fboxrule}{0.8pt}%
%\setlength{\shadowsize}{0pt}%
%\shadowbox}{}

$$\begin{center} {\xiaochuhao \CJKfamily{kd}{Xionger问题与解答} }\\ {\yihao \CJKfamily{kd}{著名的积分和几何问题} }\\ {\sihao 微信公众号:Xionger的数学小屋\quad 投稿: 2609480070@qq.com} \end{center}$$

{\erhao

\definecolor{shadethmcolor}{cmyk}{0,.13,.11,0}
\definecolor{shaderulecolor}{cmyk}{0,0.88,0.85,0.35}
$$\begin{theorem} (XPS021, Ahmed's Integral)求证 \begin{align*} \int_0^1 {\frac{{\arctan \sqrt {{x^2} + 2} }}{{\left( {{x^2} + 1} \right)\sqrt {{x^2} + 2} }}dx} = \frac{{5{\pi ^2}}}{{96}}. \end{align*} \end{theorem}$$ }
{\sihao
\begin{Solution}
(陈洪葛)
$$\begin{align*} \frac{\pi ^2}{16}&=\int_0^1{\int_0^1{\frac{dxdy}{\left( 1+x^2 \right) \left( 1+y^2 \right)}}}\\ &=\int_0^1{\int_0^1{\frac{1}{\left( 1+x^2 \right) \left( 2+x^2+y^2 \right)}+\frac{1}{\left( 1+y^2 \right) \left( 2+x^2+y^2 \right)}dxdy}}\\ &=2\int_0^1{\int_0^1{\frac{1}{\left( 1+x^2 \right) \left( 2+x^2+y^2 \right)}dydx}}=2\int_0^1{\frac{1}{\left( 1+x^2 \right) \sqrt{2+x^2}}\arctan \frac{1}{\sqrt{2+x^2}}dx}\\ &=2\int_0^1{\left( \frac{\pi}{2\left( 1+x^2 \right) \sqrt{2+x^2}}-\frac{\arctan \sqrt{2+x^2}}{\left( 1+x^2 \right) \sqrt{2+x^2}} \right) dx}=\frac{\pi ^2}{6}-2\int_0^1{\frac{\arctan \sqrt{2+x^2}}{\left( 1+x^2 \right) \sqrt{2+x^2}}dx}. \end{align*}$$
因此
$$\int_0^1{\frac{\arctan \sqrt{2+x^2}}{\left( 1+x^2 \right) \sqrt{2+x^2}}dx}=\frac{5}{96}\pi ^2.$$

(Xionger)先作一些准备工作.

令$t = \frac{{\sqrt {{x^2} + 2} }}{x}$,我们有
$$\int_1^{ + \infty } {\frac{{dx}}{{\left( {{x^2} + 1} \right)\sqrt {{x^2} + 2} }}} = \int_1^{\sqrt 3 } {\frac{{dt}}{{{t^2} + 1}}} = \frac{\pi }{{12}}.$$

令$t = \frac{1}{x}$,我们有
$$\int_1^{ + \infty } {\frac{{dx}}{{\left( {{x^2} + 1} \right)\sqrt {{x^2} + 2} }}} = \int_0^1 {\frac{t}{{\left( {{t^2} + 1} \right)\sqrt {1 + 2{t^2}} }}dt} = \frac{\pi }{{12}}.$$

而
$$\begin{align*} \int_0^{ + \infty } {\frac{{\arctan \sqrt {{x^2} + 2} }}{{\left( {{x^2} + 1} \right)\sqrt {{x^2} + 2} }}dx} = &\int_0^{ + \infty } {\frac{{dx}}{{\left( {{x^2} + 1} \right)\sqrt {{x^2} + 2} }}} \int_0^1 {\frac{{\sqrt {{x^2} + 2} }}{{1 + \left( {{x^2} + 2} \right){y^2}}}dy} \\ = &\int_0^1 {\frac{{dy}}{{{y^2}}}} \int_0^{ + \infty } {\frac{{dx}}{{\left( {{x^2} + 1} \right)\left( {{x^2} + 2 + 1/{y^2}} \right)}}} \\ =& \int_0^1 {\frac{\pi }{2} \cdot \frac{1}{{{y^2} + 1}}\left( {1 - \frac{y}{{\sqrt {2{y^2} + 1} }}} \right)dy} \\ = &\frac{{{\pi ^2}}}{{12}}. \end{align*}$$
回到原来的问题.
$$\begin{align*} \int_0^1 {\frac{{\arctan \sqrt {{x^2} + 2} }}{{\left( {{x^2} + 1} \right)\sqrt {{x^2} + 2} }}dx} &= \int_0^1 {\frac{{dx}}{{\left( {{x^2} + 1} \right)\sqrt {{x^2} + 2} }}} \int_0^1 {\frac{{\sqrt {{x^2} + 2} }}{{1 + \left( {{x^2} + 2} \right){y^2}}}dy} \\ &= \int_0^1 {\frac{{dy}}{{{y^2}}}} \int_0^1 {\frac{{dx}}{{\left( {{x^2} + 1} \right)\left( {{x^2} + 2 + 1/{y^2}} \right)}}} \\ &= \int_0^1 {\left( {\frac{\pi }{4} \cdot \frac{1}{{{y^2} + 1}} - \frac{y}{{\left( {{y^2} + 1} \right)\sqrt {2{y^2} + 1} }}\arctan \frac{y}{{\sqrt {2{y^2} + 1} }}} \right)dy} \\ & = \frac{{{\pi ^2}}}{{16}} - \int_0^1 {\frac{y}{{\left( {{y^2} + 1} \right)\sqrt {2{y^2} + 1} }}\arctan \frac{y}{{\sqrt {2{y^2} + 1} }}dy} \\ &= \frac{{{\pi ^2}}}{{16}} - \int_1^{ + \infty } {\frac{{\arctan \frac{1}{{\sqrt {{t^2} + 2} }}}}{{\left( {{t^2} + 1} \right)\sqrt {{t^2} + 2} }}dt} \quad \left( {t = \frac{1}{y}} \right). \end{align*}$$

由于
$$\int_1^{ + \infty } {\frac{{\arctan \sqrt {{x^2} + 2} }}{{\left( {{x^2} + 1} \right)\sqrt {{x^2} + 2} }}dx} + \int_1^{ + \infty } {\frac{{\arctan \frac{1}{{\sqrt {{t^2} + 2} }}}}{{\left( {{t^2} + 1} \right)\sqrt {{t^2} + 2} }}dt} = \frac{\pi }{2}\int_1^{ + \infty } {\frac{1}{{\left( {{x^2} + 1} \right)\sqrt {{x^2} + 2} }}dx} = \frac{{{\pi ^2}}}{{24}}.$$
进而有
$$\begin{align*} \int_0^1 {\frac{{\arctan \sqrt {{x^2} + 2} }}{{\left( {{x^2} + 1} \right)\sqrt {{x^2} + 2} }}dx} &= \frac{{{\pi ^2}}}{{16}} - \frac{{{\pi ^2}}}{{24}} + \int_1^{ + \infty } {\frac{{\arctan \sqrt {{x^2} + 2} }}{{\left( {{x^2} + 1} \right)\sqrt {{x^2} + 2} }}dx} \\ &= \frac{{{\pi ^2}}}{{48}} + \int_1^{ + \infty } {\frac{{\arctan \sqrt {{x^2} + 2} }}{{\left( {{x^2} + 1} \right)\sqrt {{x^2} + 2} }}dx}. \end{align*}$$
因此
$$\begin{cases} \int_0^1 {\frac{{\arctan \sqrt {{x^2} + 2} }}{{\left( {{x^2} + 1} \right)\sqrt {{x^2} + 2} }}dx} - \int_1^{ + \infty } {\frac{{\arctan \sqrt {{x^2} + 2} }}{{\left( {{x^2} + 1} \right)\sqrt {{x^2} + 2} }}dx} = \frac{{{\pi ^2}}}{{48}},\\ \int_0^1 {\frac{{\arctan \sqrt {{x^2} + 2} }}{{\left( {{x^2} + 1} \right)\sqrt {{x^2} + 2} }}dx} + \int_1^{ + \infty } {\frac{{\arctan \sqrt {{x^2} + 2} }}{{\left( {{x^2} + 1} \right)\sqrt {{x^2} + 2} }}dx} = \frac{{{\pi ^2}}}{{12}}. \end{cases}$$
故
$$\int_0^1 {\frac{{\arctan \sqrt {{x^2} + 2} }}{{\left( {{x^2} + 1} \right)\sqrt {{x^2} + 2} }}dx} = \frac{{5{\pi ^2}}}{{96}},\int_1^{ + \infty } {\frac{{\arctan \sqrt {{x^2} + 2} }}{{\left( {{x^2} + 1} \right)\sqrt {{x^2} + 2} }}dx} = \frac{{{\pi ^2}}}{{32}}.$$
\end{Solution}

[1] Definitely an Integral: 10884, Zafar Ahmed, Knut Dale and George L. Lamb Jr. The American Mathematical Monthly Vol. 109, No. 7 (Aug. - Sep., 2002), pp. 670-671 (2 pages)
}

{\sihao

\definecolor{shadethmcolor}{cmyk}{0,.13,.11,0}
\definecolor{shaderulecolor}{cmyk}{0,0.88,0.85,0.35}
\begin{theorem}
(XPS022, Coxeter’s integrals) MSE论坛的Sangchul Lee (以前的昵称SOS 440,韩国首尔大学毕业,目前在UCLA读概率方向的Ph.D)曾研究过以下一系列定积分:
$$\begin{align*} &\int_0^{\frac{\pi}{2}}{\arccos \frac{\cos x}{1+2\cos x}dx}=\frac{5\pi ^2}{24},&&\int_0^{\frac{\pi}{3}}{\arccos \frac{\cos x}{1+2\cos x}dx}=\frac{2\pi ^2}{15},\\ &\int_0^{\frac{\pi}{2}}{\arccos \frac{1}{1+2\cos x}dx}=\frac{\pi ^2}{6},&&\int_0^{\frac{\pi}{3}}{\arccos \frac{1}{1+2\cos x}dx}=\frac{\pi ^2}{8},\\ &\int_0^{\arccos \frac{1}{3}}{\arccos \frac{1-\cos x}{2\cos x}dx}=\frac{\pi ^2}{6},&&\int_0^{\frac{\pi}{3}}{\arccos \frac{1-\cos x}{2\cos x}dx}=\frac{11}{72}\pi ^2,\\ &\int_0^{\frac{\pi}{2}}{\arccos \sqrt{\frac{\cos x}{1+2\cos x}}dx}=\frac{\pi ^2}{6},&&\int_0^{\frac{\pi}{3}}{\arccos \sqrt{\frac{\cos x}{1+2\cos x}}dx}=\frac{5\pi ^2}{48}. \end{align*}$$

$$\begin{align*} &\int_0^{\frac{\pi}{5}}{\arccos}\left( \frac{3+\sqrt{5}-2\left( \sqrt{5}+2 \right) \cos x}{1+\sqrt{5}-2\left( \sqrt{5}+3 \right) \cos x} \right) dx=\frac{11\pi ^2}{150},\\ &\int_0^{\frac{3\pi}{5}}{\arccos}\left( \frac{3-\sqrt{5}+2\left( \sqrt{5}-2 \right) \cos x}{1-\sqrt{5}+2\left( \sqrt{5}-3 \right) \cos x} \right) dx=\frac{61\pi ^2}{150}. \end{align*}$$
\end{theorem}}
{\sihao
$$\begin{Solution} 下面贴出其中一个积分的解答过程,由西西(王永喜)在某论坛给出. \begin{align*} &\int_0^{\frac{\pi}{3}}{\arccos \left( \frac{1-\cos x}{\text{2}\cos x} \right) dx}=\int_0^{\frac{\pi}{3}}{\text{2}\arctan \sqrt{\frac{\text{3}\cos x-1}{\cos x+1}}dx} \\ &=\int_0^{\pi}{\text{4}\arctan \sqrt{\frac{\text{3}\cos 2y-1}{\cos 2y+1}}dy}\quad \left( x=2y \right) \\ &=\int_0^{\frac{\pi}{6}}{\text{4}\arctan \left( \frac{\sqrt{1-\text{3}\sin ^2y}}{\cos y} \right) dy}=\int_0^{\frac{\pi}{6}}{4\left[ \frac{\pi}{2}-\arctan \left( \frac{\cos y}{\sqrt{1-\text{3}\sin ^2y}} \right) \right] dy} \\ &=\frac{\pi ^2}{3}-4\int_0^{\frac{\pi}{6}}{\arctan \left( \frac{\cos y}{\sqrt{1-\text{3}\sin ^2y}} \right) dy} \\ &=\frac{\pi ^2}{3}-4\int_0^{\frac{\pi}{6}}{\int_0^1{\frac{\cos y}{\sqrt{1-\text{3}\sin ^2y}}\frac{dt}{1-\left( \frac{1-\sin ^2y}{1-\text{3}\sin ^2y} \right) t^2}dy}} \\ &=\frac{\pi ^2}{3}-\int_0^{\frac{\pi}{6}}{\int_0^1{\frac{\text{4}\cos y\sqrt{1-\text{3}\sin ^2y}dt}{\left( 1-\text{3}\sin ^2y \right) +\left( 1-\sin ^2y \right) t^2}dy}} \\ &=\frac{\pi ^2}{3}-\int_0^{\frac{\pi}{3}}{\int_0^1{\frac{4\sqrt{3}\cos ^2wdt}{\text{3}\cos ^2w+\left( 2+\cos ^2w \right) t^2}dw}}\quad \left( \sin w=\sqrt{3}\sin y \right) \\ &=\frac{\pi ^2}{3}-\int_0^{\frac{\pi}{3}}{\int_0^1{\frac{4\sqrt{3}\sec ^2wdt}{\left[ \left( 3+3t^2 \right) +2t^2\tan ^2w \right] \left( 1+\tan ^2w \right)}dw}} \\ &=\frac{\pi ^2}{3}-\int_0^{\sqrt{3}}{\int_0^1{\frac{4\sqrt{3}dtds}{\left[ \left( 3+3t^2 \right) +2t^2s^2 \right] \left( 1+s^2 \right)}}}\ \ \left( s=\tan w \right) \\ &=\frac{\pi ^2}{3}-\int_0^{\sqrt{3}}{\int_0^1{\frac{4\sqrt{3}}{t^2+3}\left( \frac{1}{1+s^2}-\frac{2t^2}{\left( 3t^2+3 \right) +2t^2s^2} \right) dtds}} \\ &=\frac{\pi ^2}{3}-\int_0^1{\frac{4\sqrt{3}}{t^2+3}\left[ \frac{\pi}{3}-\sqrt{\frac{2t^2}{3t^2+3}}\arctan \left( \sqrt{\frac{2t^2}{t^2+1}} \right) \right] dt} \\ &=\frac{\pi ^2}{9}+4\sqrt{2}\int_0^1{\frac{t}{\left( t^2+3 \right) \sqrt{t^2+1}}\arctan \left( \frac{t\sqrt{2}}{\sqrt{t^2+1}} \right) dt} \\ &=\frac{\pi ^2}{9}+\left[ \text{4}\tan ^{-1}\left( \frac{\sqrt{t^2+1}}{\sqrt{2}} \right) \tan ^{-1}\left( \frac{t\sqrt{2}}{\sqrt{t^2+1}} \right) \right] _{0}^{1}\\ &\quad-4\sqrt{2}\int_0^1{\frac{1}{\left( 3t^2+1 \right) \sqrt{t^2+1}}}\tan ^{-1}\left( \frac{\sqrt{t^2+1}}{\sqrt{2}} \right) dt \\ &=\frac{13\pi ^2}{36}-4\sqrt{2}\int_0^1{\frac{1}{\left( 3t^2+1 \right) \sqrt{t^2+1}}\tan ^{-1}\left( \frac{\sqrt{t^2+1}}{\sqrt{2}} \right) dt} \\ &=\frac{5\pi ^2}{36}-\int_0^1{\frac{4}{3t^2+1}\int_0^1{\frac{1}{1+\left( \frac{t^2+1}{2} \right) u^2}}dudt} \\ &=\frac{13\pi ^2}{36}-4\int_0^1{\int_0^1{\frac{1}{u^2+3}\left[ \frac{1}{t^2+\frac{1}{3}}-\frac{1}{t^2+\frac{u^2+2}{u^2}} \right] dudt}} \\ &=\frac{5\pi ^2}{36}+4\int_0^1{\frac{u}{\left( u^2+3 \right) \sqrt{u^2+2}}\tan ^{-1}\left( \frac{u}{\sqrt{u^2+2}} \right) du} \\ &=\frac{5\pi ^2}{36}+4\left[ \tan ^{-1}\sqrt{u^2+2}\tan ^{-1}\left( \frac{u}{\sqrt{u^2+2}} \right) \right] _{0}^{1}-4\int_0^1{\frac{\tan ^{-1}\sqrt{u^2+2}}{\left( u^2+1 \right) \sqrt{u^2+2}}du} \\ &=\frac{13\pi ^2}{36}-4\int_0^1{\frac{\tan ^{-1}\sqrt{u^2+2}}{\left( u^2+1 \right) \sqrt{u^2+2}}du}=\frac{13\pi ^2}{36}-\frac{5\pi ^2}{24}=\frac{11\pi ^2}{72}. \end{align*} \end{Solution}$$

%\textbf{注.}本题的分布函数是比较复杂的,我用如下的方法尝试了进行计算:

[1] H. S. M. Coxeter. The functions of Schlafli and Lobatschefsky. The Quarterly Journal of Mathematics, (1):13–29, 1935.

[2] H. S. M. Coxeter. A challenging definite integral. Am. Math. Mon., 95:330, 1988.
}

{\erhao
\definecolor{shadethmcolor}{cmyk}{0,.13,.11,0}
\definecolor{shaderulecolor}{cmyk}{0,0.88,0.85,0.35}
$$\begin{theorem} (XPS023,本本蛋蛋的问题,后面的积分由向老师给出解答)正三角形带电薄片(带正电荷)位于\(\,\Sigma\colon\,x+y+z=-a\)（其中\(\,a>0\)）的平面上，且带电薄片限定于\(-a\le x\le 0\)与\(-a\le y\le 0\)之间,其电荷面密度为\(\sigma\),试求出原点处的电场强度\(\boldsymbol{E}\) (矢量). \end{theorem}$$
}

{\sihao
\begin{Solution}

$$\left|\overrightarrow{\boldsymbol{E}}\,\right|\,=\sqrt{3}\displaystyle\iint\limits_{\Sigma\colon\,x+y+z=-a}\dfrac{\sigma\,\,{\rm\,d}S}{4\pi\varepsilon_0\left(x^2+y^2+z^2\right)}\dfrac{\left|x\right|}{\sqrt{x^2+y^2+z^2}}$$

$$\big|\overrightarrow{\boldsymbol{E}}\big|\,\cos\langle\overrightarrow{\boldsymbol{E}},\overrightarrow{\boldsymbol{i}}\rangle=\displaystyle\iint\limits_{\Sigma\colon\,x+y+z=-a}\dfrac{\sigma\,\left|x\right|\,{\rm\,d}S}{4\pi\varepsilon_0\left(x^2+y^2+z^2\right)^{\frac{3}{2}}}$$
$$\big|\overrightarrow{\boldsymbol{E}}\big|\,\cos\langle\overrightarrow{\boldsymbol{E}},\overrightarrow{\boldsymbol{j}}\rangle=\displaystyle\iint\limits_{\Sigma\colon\,x+y+z=-a}\dfrac{\sigma\,\left|y\right|\,{\rm\,d}S}{4\pi\varepsilon_0\left(x^2+y^2+z^2\right)^{\frac{3}{2}}}$$
$$\big|\overrightarrow{\boldsymbol{E}}\big|\,\cos\langle\overrightarrow{\boldsymbol{E}},\overrightarrow{\boldsymbol{k}}\rangle=\displaystyle\iint\limits_{\Sigma\colon\,x+y+z=-a}\dfrac{\sigma\,\left|z\right|\,{\rm\,d}S}{4\pi\varepsilon_0\left(x^2+y^2+z^2\right)^{\frac{3}{2}}}$$

$$\begin{align*} \big|\overrightarrow{\boldsymbol{E}}\big|\,&=\sqrt{3}\displaystyle\iint\limits_{\Sigma\colon\,x+y+z=-a}\dfrac{\sigma\,\left|x\right|\,{\rm\,d}S}{4\pi\varepsilon_0\left(x^2+y^2+z^2\right)^{\frac{3}{2}}}\\ &=\frac{\sqrt{3}\,\sigma}{4\pi\varepsilon_0} \displaystyle\iint\limits_{\Sigma\colon\,x+y+z=-a}\dfrac{\,\left|x\right|\,}{\left(x^2+y^2+z^2\right)^{\frac{3}{2}}}{\rm\,d}S\\ &=\frac{\sqrt{3}\,\sigma}{4\pi\varepsilon_0} \int_{-a}^0\int_{-a-y}^0 \dfrac{\sqrt{3}\,\left|x\right|}{\left(x^2+y^2+\left(-a-x-y\right)^2\right)^{\frac{3}{2}}}{\rm\,d}x{\rm\,d}y\\ &=\frac{\sqrt{3}\,\sigma}{4\pi\varepsilon_0} \int_{-a}^0\int_{-a-y}^0 \dfrac{\sqrt{3}\,\left|x\right|}{\left(x^2+y^2+\left(a+x+y\right)^2\right)^{\frac{3}{2}}}{\rm\,d}x{\rm\,d}y\\ &=\frac{\sqrt{3}\,\sigma}{4\pi\varepsilon_0} \int_0^a\int_0^{a-y} \dfrac{\sqrt{3}\,x}{\left(x^2+y^2+\left(a-x-y\right)^2\right)^{\frac{3}{2}}}{\rm\,d}x{\rm\,d}y\\ &=\frac{3\,\sigma}{4\pi\varepsilon_0} \int_0^a\int_0^{a-y} \dfrac{\,x}{\left(x^2+y^2+\left(a-x-y\right)^2\right)^{\frac{3}{2}}}{\rm\,d}x{\rm\,d}y\\ \end{align*}$$

$$\begin{align*} \color{red}{\boxed{\quad\color{black}{\int_0^a\int_0^{a-y} \dfrac{\,x}{\left(x^2+y^2+\left(a-x-y\right)^2\right)^{\frac{3}{2}}}{\rm\,d}x{\rm\,d}y\,=\,\frac{\pi}{6}}\quad}} \end{align*}$$
\end{Solution}

}

{\erhao
\definecolor{shadethmcolor}{cmyk}{.10,.10,0,0}
\definecolor{shaderulecolor}{cmyk}{.75,.75,0,.5}
$$\begin{theorem} (XPS024, IBM官网的挑战题, August 1998)平面上有一个三角形$ABC$,若点$D,E,F$分别在边$AB,BC,CA$上,且$\triangle DEF$为正三角形, $AD=BE=CF$.求证: $\triangle ABC$也为正三角形. \end{theorem}$$
}

\end{document}

 

\documentclass[11pt,no-math,a4paper]{article}
\RequirePackage{xeCJK}

%%%修改数学字体
\usepackage{fontspec}
\usepackage[T1]{fontenc}
\usepackage{times}
\usepackage[complete,amssymbols,amsbb,eufrak,nofontinfo,
subscriptcorrection,zswash,mtpscr]{mtpro2}

%\usepackage{mathpazo}
%\renewcommand{\rmdefault}{ibh}
%\usepackage{fourier}
%\usepackage{charter}
%\usepackage{helvet}
\usepackage{amsmath,amsthm}
%%%修改数学字体
%\usepackage{CJKnumb}
%\usepackage{amsmath,amssymb,amsthm}

\setCJKmainfont[BoldFont={方正黑体简体},ItalicFont={方正楷体简体}]{方正书宋简体}
%\setCJKsansfont[BoldFont={黑体}]{方正中等线简体}
%\setCJKmonofont{方正中等线简体}

\setCJKfamilyfont{kd}{华文行楷}
\setmainfont{Times New Roman}
\setsansfont{DejaVu Sans}
\setmonofont{Latin Modern Mono}

\setCJKfamilyfont{song}{方正书宋简体}
\newcommand{\song}{\CJKfamily{song}}
\setCJKfamilyfont{hei}{方正黑体简体}
\newcommand{\hei}{\CJKfamily{hei}}
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

\newcommand{\chaoda}{\fontsize{55pt}{\baselineskip}\selectfont}
\newcommand{\chuhao}{\fontsize{42pt}{\baselineskip}\selectfont} % 字号设置
\newcommand{\xiaochuhao}{\fontsize{36pt}{\baselineskip}\selectfont} % 字号设置
\newcommand{\yihao}{\fontsize{28pt}{\baselineskip}\selectfont} % 字号设置
\newcommand{\erhao}{\fontsize{21pt}{\baselineskip}\selectfont} % 字号设置
\newcommand{\xiaoerhao}{\fontsize{18pt}{\baselineskip}\selectfont} % 字号设置
\newcommand{\sanhao}{\fontsize{15.75pt}{\baselineskip}\selectfont} % 字号设置
\newcommand{\xiaosanhao}{\fontsize{15pt}{\baselineskip}\selectfont} % 字号设置
\newcommand{\sihao}{\fontsize{14pt}{\baselineskip}\selectfont} % 字号设置
\newcommand{\xiaosihao}{\fontsize{12pt}{14pt}\selectfont} % 字号设置
\newcommand{\wuhao}{\fontsize{10.5pt}{12.6pt}\selectfont} % 字号设置
\newcommand{\xiaowuhao}{\fontsize{9pt}{11pt}{\baselineskip}\selectfont} % 字号设置
\newcommand{\liuhao}{\fontsize{7.875pt}{\baselineskip}\selectfont} % 字号设置
\newcommand{\qihao}{\fontsize{5.25pt}{\baselineskip}\selectfont} % 字号设置

 

 

 

\usepackage{tikz}
\usepackage{makeidx}
\usepackage{enumitem}
%\usepackage[left=2.6cm,right=2.6cm,top=2.54cm,bottom=2.54cm]{geometry}
\usepackage[body={16cm,26.67cm}, left=0.6cm,right=0.6cm,top=0.54cm,bottom=0.54cm]{geometry}
%\geometry{papersize={480mm,800mm}}
%\usepackage{mathtools}
%\usepackage{mathrsfs}

\usepackage{multirow,booktabs}
\usepackage{makecell}
%\title{中国科学技术大学\\
%2015年硕士学位研究生入学考试试题}
%\author{(线性代数与解析几何)}
%\date{}

%\newenvironment{newproof}{\par\CJKfamily{xiao}\noindent{\makebox[0pt][r]{\;\;}\textbf{证明:}}\color{black!90}\small}{\hfill$\Box$\quad\par}

%\newenvironment{solution}{\par\CJKfamily{xiao}\noindent{\makebox[0pt][r]{\;\;}\textbf{解:}}\small}{\hfill$\Box$\quad\par}

\newenvironment{Proof}{\par\noindent{\hei 证明}\hspace{1em}}{\qed\par}
\newenvironment{Answer}{\par\noindent{\hei 答}\hspace{1em}}{\par\song}
\newenvironment{Solution}{\par\noindent{\hei 解}\hspace{1em}}{\hfill$\lhd$\par\vspace{6pt}\song}
\newcommand{\Ker}{\mathrm{Ker}\,}

\usepackage{fancyhdr}
\usepackage{fancybox}
\usepackage{lastpage}%此宏包是获取总页数用的。
\pagestyle{fancy}
\renewcommand{\headrulewidth}{0pt}%设置页眉线
\renewcommand{\footrulewidth}{1pt}%设置页脚线

\fancyhf{}%清除所有页眉页脚

\lfoot{科目名称：数学}
\cfoot{}
\rfoot{第\thepage 页\quad 共\pageref{LastPage} 页}

\usepackage{shadethm}
\newshadetheorem{theorem}{}%[section]
%\shadetheoremstyle{plain}

\begin{document}
%\maketitle

%\fancypage{%
%\setlength{\fboxsep}{13pt}%
%\setlength{\fboxrule}{0.8pt}%
%\setlength{\shadowsize}{0pt}%
%\shadowbox}{}

$$\begin{center} {\xiaochuhao \CJKfamily{kd}{Xionger问题与解答} }\\ {\yihao \CJKfamily{kd}{18博的几道初等概率问题} }\\ {\sihao 微信公众号:Xionger的数学小屋\quad 投稿: 2609480070@qq.com} \end{center}$$

{\erhao

\definecolor{shadethmcolor}{cmyk}{0,.13,.11,0}
\definecolor{shaderulecolor}{cmyk}{0,0.88,0.85,0.35}
$$\begin{theorem} 一个游戏$100$关,每关得花费一分钟,并且有$1/2$的概率通关.如果某一关没过就得从第一关重新开始,概率还是$1/2$通过,求通关时间的期望. \end{theorem}$$ }
{\sihao
$$\begin{Solution} 记$X=X_1+X_2+\cdots+X_n$为通关时间,其中$X_i$表示通过整个游戏,即通过第$100$关时在第$i$关玩了多少次, $1\leq i\leq 100$.注意到$\mathbb{E}[X_{100}]=2$且$\mathbb{E}[X_{i-1}]=2\mathbb{E}[X_i]$,因此 \begin{align*} \mathbb{E}\left[ X \right] &=\mathbb{E}\left[ \sum_{i=1}^{100}{X_i} \right] =\sum_{i=1}^{100}{\mathbb{E}\left[ X_i \right]}=\sum_{i=1}^{100}{2^{101-i}}\\ &=\sum_{i=1}^{100}{2^i}=2^{101}-2. \end{align*} \end{Solution}$$

\textbf{注.}本题的分布函数是比较复杂的,我用如下的方法尝试了进行计算:

记通关时间为$n\geq 100$.
\begin{enumerate}
\item[(1)] 若$n=100$,则该玩家必定一口气通过所有的100关,概率为$\displaystyle\frac{1}{2^{100}}$;

\item[(2)] 若$n=101$,则该玩家先跪在第一关,然后重新开始一口气通过所有的100关,概率为$\displaystyle(1-\frac{1}{2})\frac{1}{2^{100}}=\frac{1}{2^{101}}$,即$1=1+0$;

\item[(3)] 若$n=102$,则该玩家可能连续两次跪在第一关,然后重新开始一口气通过所有的100关;可能先是跪在第二关,然后重新开始一口气通过所有的100关.总的概率为$\displaystyle\frac{2}{2^{102}}=\frac{1}{2^{101}}$,即$2=1+1=2+0$;

\item[(4)] 若$n=103$,则该玩家可能连续三次跪在第一关,然后重新开始一口气通过所有的100关;可能先是跪在第二关,然后跪在第一关,接着重新开始一口气通过所有的100关;可能先是跪在第一关,然后跪在第二关,接着重新开始一口气通过所有的100关;另外一种可能是先跪在第三关,然后重新开始一口气通过所有的100关.总的概率为$\displaystyle\frac{4}{2^{103}}=\frac{1}{2^{101}}$,即$3=1+1+1=1+2=2+1=3+0$;
\end{enumerate}

如此类推$4=1+1+1+1=1+1+2=1+2+1=2+1+1=3+1=1+3=2+2=4+0$,总共8种分拆方式.对于更大的$n$,分拆个数也有此规律,因此我猜测:

\textcolor[rgb]{0.00,0.50,0.00}{对于正整数$n$,满足题意的整数分拆有$2^{n-1}$种.}

由此可得$N=100+n$的概率为
$$\frac{2^{n-1}}{2^N}=\frac{1}{2^{N+1-n}}=\frac{1}{2^{101}}.$$
故所求期望为
$$E=\frac{100}{2^{100}}+\sum_{N=101}^{\infty}{\frac{N}{2^{101}}}\rightarrow \infty.$$
这说明,此款游戏永远不能通过所有关卡,这是荒谬的!

我很迷惑,求助于冯w,他告诉我里面存在一个分拆的问题,比如$200=199+1$,这意味着玩家首先没通过第$199$关,然后没通过第1关;然而本游戏只有100关,这就出现了问题!
}

{\erhao
\definecolor{shadethmcolor}{cmyk}{0,.13,.11,0}
\definecolor{shaderulecolor}{cmyk}{0,0.88,0.85,0.35}
$$\begin{theorem} 在$(0,1)$上的均匀分布中随机取数,若随机取$n$个数,当它们的求和第一次大于$1$时,就把这个$n$记录下来.求记录下的这个数的期望. \end{theorem}$$
}

{\sihao
\begin{Solution}
令$X_1,X_2,\ldots,X_n\sim U(0,1)$, $S_0=0,S_n=X_1+X_2+\cdots+X_n$,定义停时
$$\tau=\inf\{n\geq 0:S_n>1\}.$$ 问题转化为求$\mathbb{E}[S_\tau]$.

我们可知$S_n-n/2$是一个鞅,因为$S_{\tau\wedge n}\leq 2$,满足最优取样定理的条件,可以得到
$\mathbb{E}[S_\tau-\tau/2]=S_0=0$,因此$\mathbb{E}[S_\tau]=\mathbb{E}[\tau]/2$,只需求$\mathbb{E}[\tau]$即可.

考虑到$\tau$是一个在$\{1,2,3,\ldots\}$上取值的计数随机变量,其期望为
$$\mathbb{E}\left[ \tau \right] =\sum_{n=1}^{\infty}{n\mathrm{Pr}\left( \tau =n \right)}=\sum_{n=1}^{\infty}{\mathrm{Pr}\left( \tau \geq n \right)},$$
这个公式可以参考钟开莱的《概率论教程》.这里,事件$\{\tau\geq n\}$等价于事件$\{X_1+\cdots+X_{n-1}\leq 1\}$,考虑正方体$A:\{(x_1,\ldots,x_n):0<x_i<1\}$以及单纯形$B:\{(x_1,\ldots,x_n):0<x_i<1,x_1+x_2+\cdots+x_n\leq 1\}$,利用$n$重积分知识可计算出$B$的体积为$V_B=\frac{1}{n!}$,因此
$$\begin{align*} \mathbb{E}\left[ \tau \right] &=\sum_{n=1}^{\infty}{\mathrm{Pr}\left( X_1+\cdots +X_{n-1}\leq 1 \right)}=\sum_{n=0}^{\infty}{\mathrm{Pr}\left( X_1+\cdots +X_n\leq 1 \right)}\\ &=\sum_{n=0}^{\infty}{\frac{V_B}{V_A}}=\sum_{n=0}^{\infty}{\frac{1}{n!}}=e, \end{align*}$$
因此所求概率为
$$\mathbb{E}[S_\tau]=\mathbb{E}[\tau]/2=\frac{e}{2}.$$
\end{Solution}

\textbf{注.}可以利用Wald方程证明
$$\mathbb{E}[S_\tau]=\mathbb{E}[\tau]\mathbb{E}[X_n]=\frac{e}{2}.$$
}

{\erhao
\definecolor{shadethmcolor}{cmyk}{.10,.10,0,0}
\definecolor{shaderulecolor}{cmyk}{.75,.75,0,.5}
$$\begin{theorem} 在一个圆周上随机取三点,求它们构成钝角三角形的概率. \end{theorem}$$
}

\end{document}