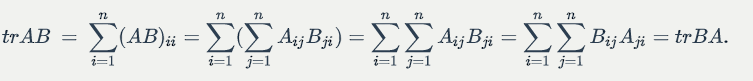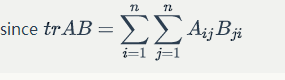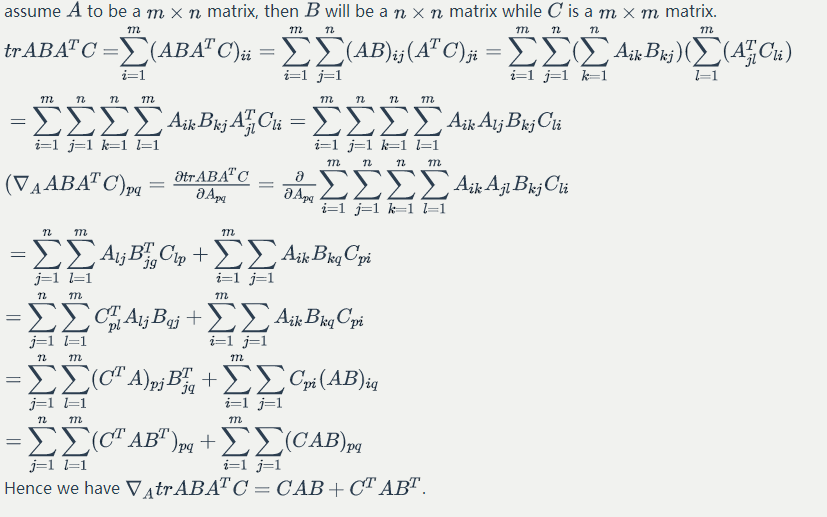CS 229 notes Supervised Learning
CS 229 notes Supervised Learning
标签(空格分隔): 监督学习 线性代数
Forword
the proof of Normal equation and, before that, some linear algebra equations, which will be used in the proof.
The normal equation
Linear algebra preparation
For two matrices and
such that
is square,
.
Proof:
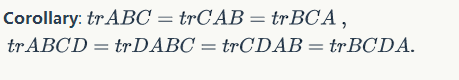
Some properties: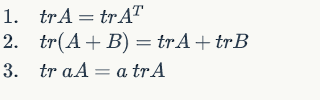
some facts of matrix derivative:
Proof:
Proof 1:
Proof 2:
Proof:
(refers to the cofactor)
Least squares revisited
(if we don’t include the intercept term)
since ,
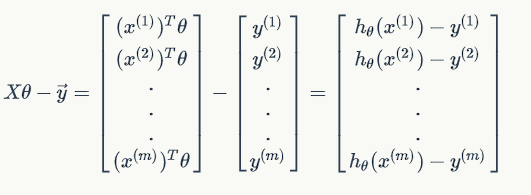
Thus,
$\frac{1}{2}(X\theta-\vec{y})^T(X\theta-\vec{y}) =
\frac{1}{2}\displaystyle{\sum{i=1}^{m}(h\theta(x^{(i)}) -y^{(i)})^2} = J(\theta) $.
Combine Equations :
Hence
Notice it is a real number, or you can see it as a matrix, so
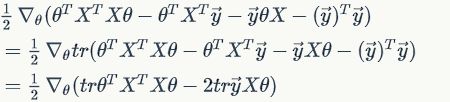
since and
involves no
elements.
then use equation with
,
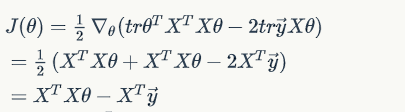
To minmize , we set its derivative to zero, and obtain the normal equation: