浅谈归并排序：合并 K 个升序链表的归并解法
在面试中遇到了这道题：如何实现多个升序链表的合并。这是 LeetCode 上的一道原题，题目具体如下：
用归并实现合并 K 个升序链表
给你一个链表数组，每个链表都已经按升序排列。
请你将所有链表合并到一个升序链表中，返回合并后的链表。
示例 1：
输入：lists = [[1,4,5],[1,3,4],[2,6]] 输出：[1,1,2,3,4,4,5,6] 解释：链表数组如下： [ 1->4->5, 1->3->4, 2->6 ] 将它们合并到一个有序链表中得到。 1->1->2->3->4->4->5->6
这题可以用归并的思想来实现，我们两两链表合并，到最后合成所有的链表。代码如下：
public ListNode mergeKLists(ListNode[] lists) {
return merge(lists, 0, lists.length - 1);
}
public ListNode merge(ListNode[] lists, int left, int right) {
if(left == right) {
return lists[left];
}
if (left > right) {
return null;
}
int mid = (left + right) >> 1;
return mergeTwoLists(merge(lists, left, mid), merge(lists, mid + 1, right));
}
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
if(l1 == null) {
return l2;
}
if(l2 == null) {
return l1;
}
ListNode head = new ListNode(-1);
ListNode cur = head;
while(l1 != null && l2 != null) {
if(l1.val < l2.val) {
cur.next = l1;
l1 = l1.next;
}else {
cur.next = l2;
l2 = l2.next;
}
cur = cur.next;
}
cur.next = l1 == null ? l2:l1;
return head.next;
}
现在我们来回顾一下归并排序的知识
一、归并排序
1. 归并排序的定义
- 基本思路：借助外部空间，合并两个有序数组/序列，得到更长的数组
- 算法思想：分而治之
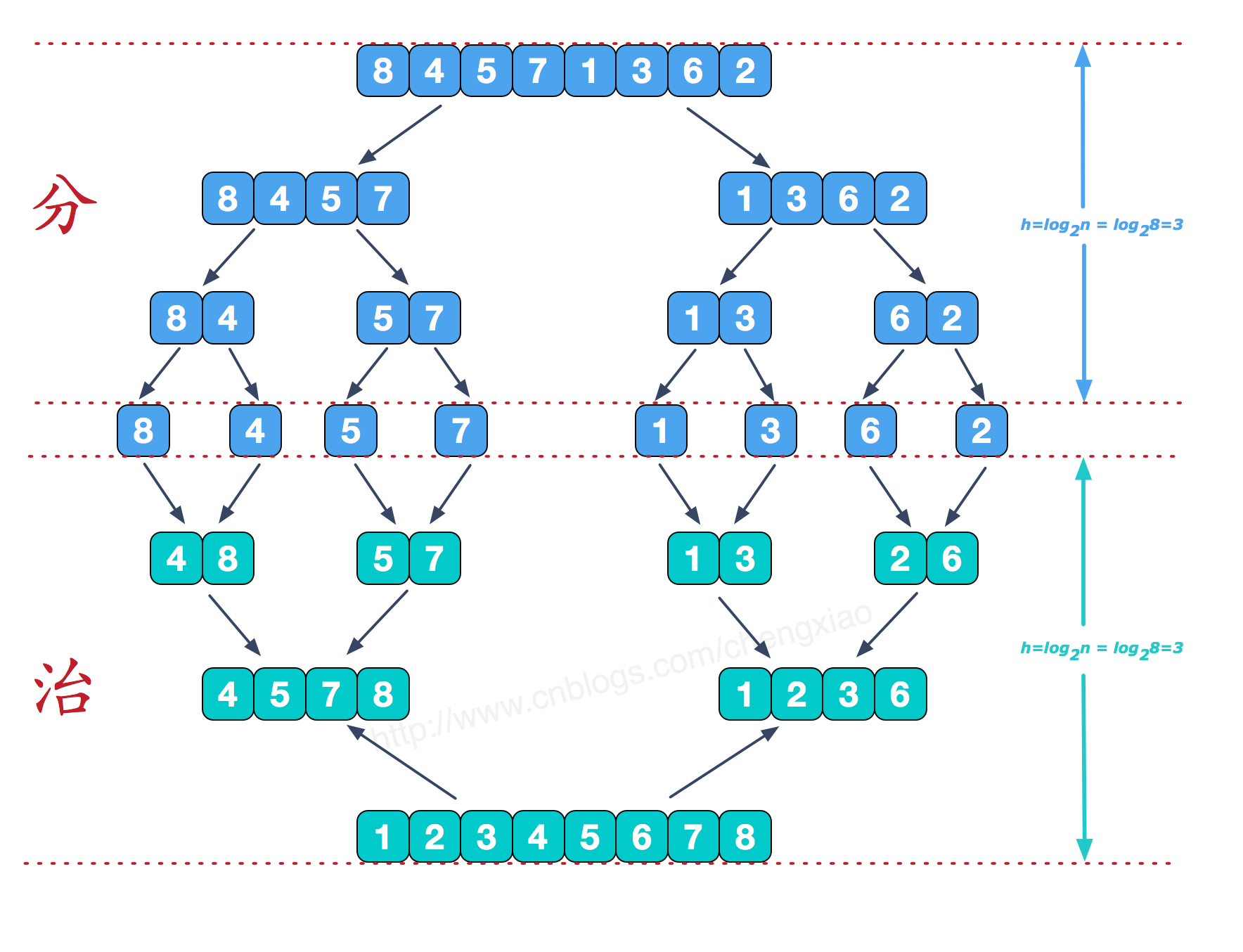
比如对于数组[8,4,5,7,1,3,6,2]的排序：整体的过程是这样：先“分”成小问题，再进行“治”操作
2.归并排序算法代码实现
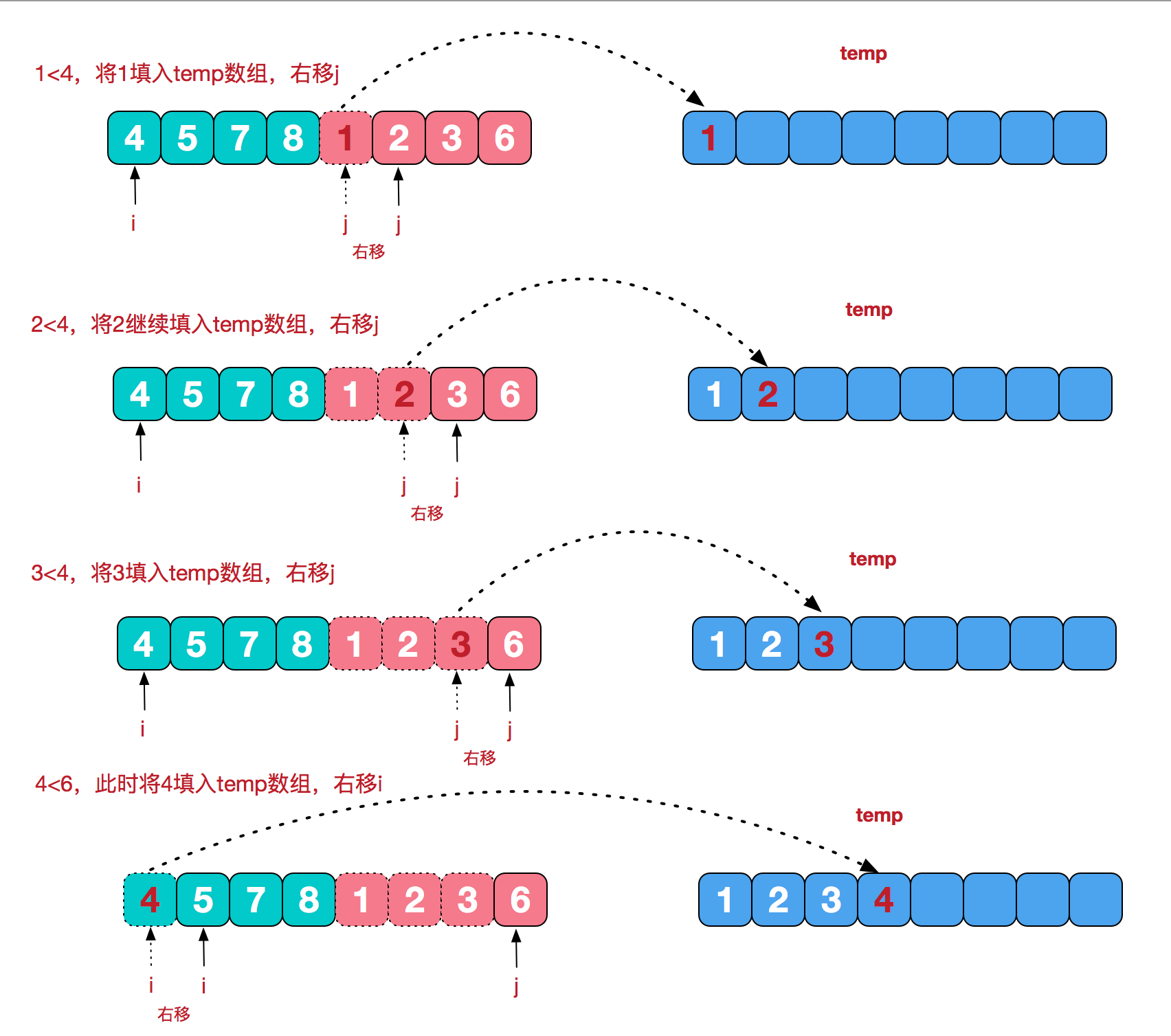
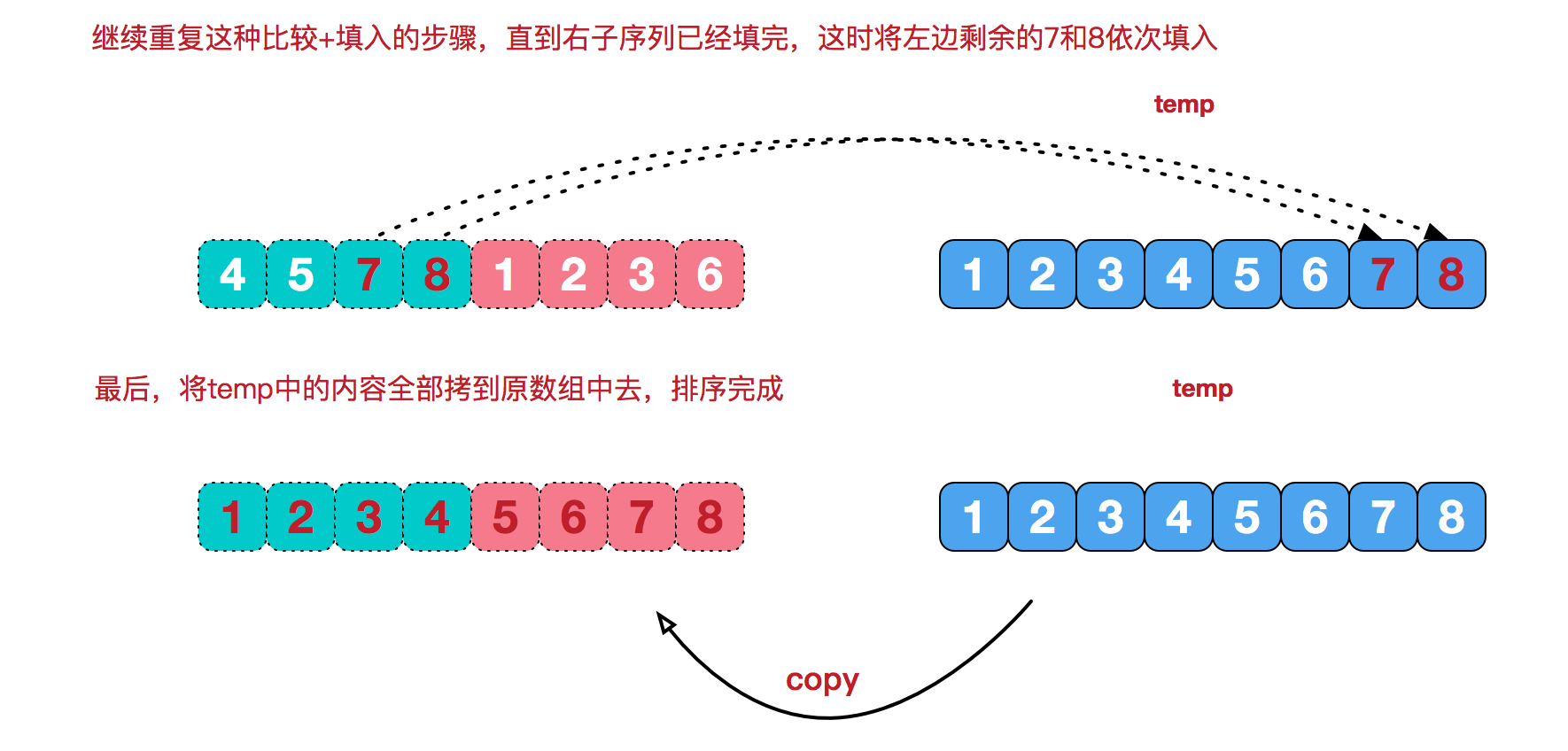
先来看看归并排序实现一个数组[8,4,5,7,1,3,6,2]的排序，难以理解的是合并相邻有序子序列这块，我们来看 [4,5,7,8] 和[1,2,3,6]这两个已经有序的子序列的合并：图片转自这篇博客图解排序算法(四)之归并排序
public int[] sortArray(int[] nums) {
int[] temp = new int[nums.length];
merge(nums, 0, nums.length - 1, temp);
return nums;
}
public void merge(int[] nums, int left, int right, int[] temp) {
if(left < right) {
int mid = (left + right) >> 1;
merge(nums, left, mid, temp);
merge(nums, mid + 1, right, temp);
mergeSort(nums, left, mid, right, temp);
}
}
public void mergeSort(int[] nums, int left, int mid, int right, int[] temp) {
int i = left;
int j = mid + 1;
for(int k = left; k <= right; k++) {
temp[k] = nums[k];
}
for(int k = left; k <= right; k++) {
//当 i 指针走完时，将 j 指针部分复制到数组中
if(i == mid +1) {
nums[k] = temp[j];
j++;
//若 j 指针走完，将 i 指针部分复制到最后数组中
}else if(j == right + 1) {
nums[k] = temp[i];
i++;
//这里的 = 是保持排序算法的稳定性，即排序后相等的数据原有顺序不变
}else if(temp[i] <= temp[j]) {
nums[k] = temp[i];
i++;
}else {
nums[k] = temp[j];
j++;
}
}
}
二、归并排序的一些经典题
1.LeetCode 88. 合并两个有序数组
给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2，另有两个整数 m 和 n ，分别表示 nums1 和 nums2 中的元素数目。
请你 合并 nums2 到 nums1 中，使合并后的数组同样按 非递减顺序 排列。
注意：最终，合并后数组不应由函数返回，而是存储在数组 nums1 中。为了应对这种情况，nums1 的初始长度为 m + n，其中前 m 个元素表示应合并的元素，后 n 个元素为 0 ，应忽略。nums2 的长度为 n 。
示例 1：
输入：nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出：[1,2,2,3,5,6]
解释：需要合并 [1,2,3] 和 [2,5,6] 。
合并结果是 [1,2,2,3,5,6] ，其中斜体加粗标注的为 nums1 中的元素。
这道题可以用归并排序的思想来完成，这里就是用的“治”操作：
public void merge(int[] nums1, int m, int[] nums2, int n) {
int[] temp = new int[m+n];
for(int t = 0; t < m; t++) {
temp[t] = nums1[t];
}
for(int t = m, g = 0; t < m + n & g < n; t++,g++) {
temp[t] = nums2[g];
}
int i = 0;
int j = m;
for(int k = 0; k < m + n; k++) {
if(i == m) {
nums1[k] = temp[j];
j++;
} else if(j == m + n) {
nums1[k] = temp[i];
i++;
} else if(temp[i] <= temp[j]) {
nums1[k] = temp[i];
i++;
} else {
nums1[k] = temp[j];
j++;
}
}
}
2.剑指 Offer 51. 数组中的逆序对
在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组，求出这个数组中的逆序对的总数。
示例 1:
输入: [7,5,6,4]
输出: 5
这题实际上还是利用数组中的元素两两配对比较，也就是分治处理，不过这次是比较大小后的计数。
public int reversePairs(int[] nums) {
int len = nums.length;
if(len < 2) {
return 0;
}
int[] temp = new int[len];
return mergePairs(nums, 0, len - 1, temp);
}
public int mergePairs(int[] nums, int left, int right, int[] temp) {
//如果是无参void 则可写成 return; 或者不写
if(left >= right) {
return 0;
}
int mid = (left + right) >> 1;
int leftCount = mergePairs(nums, left, mid, temp);
int rightCount = mergePairs(nums, mid + 1, right, temp);
int reverseCount = merge(nums, left, mid, right, temp);
//最后记得返回三者之和
return leftCount + rightCount + reverseCount;
}
public int merge(int[] nums, int left, int mid, int right, int[] temp) {
int i = left;
int j = mid + 1;
int count = 0;
for(int t = left; t <= right; t++) {
temp[t] = nums[t];
}
for(int k = left; k <= right; k++) {
if(i == mid + 1) {
nums[k] = temp[j++];
} else if(j == right + 1 || temp[i] <= temp[j]) {
nums[k] = temp[i++];
} else {
nums[k] = temp[j++];
count += mid - i + 1;
}
}
return count;
}
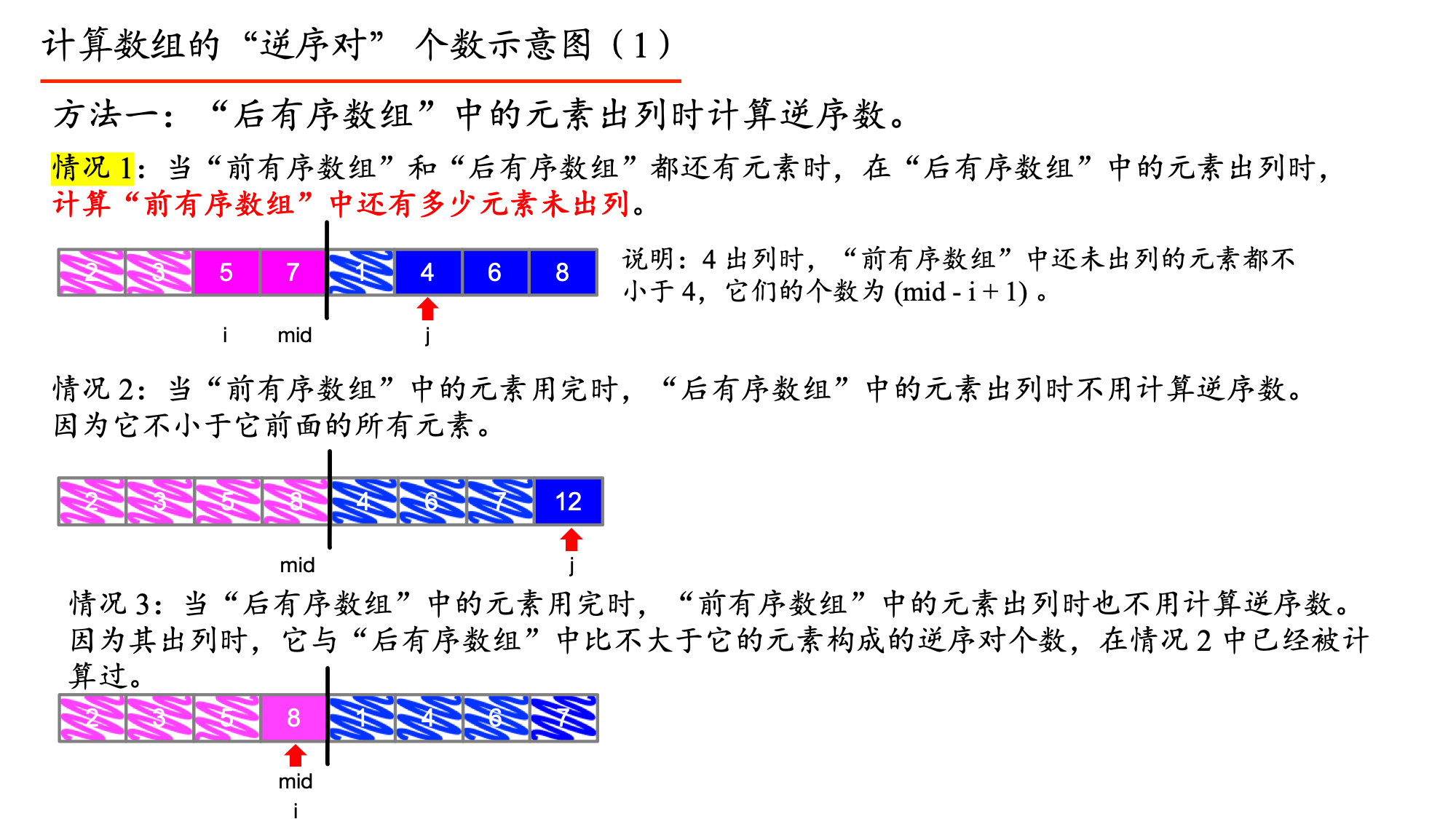
这里要说一下逆序数的求法：前提是两个序列有序
如果有两个有序序列：
Seq1：3 4 5
Seq2：2 6 8 9
对于序列seq1中的某个数a[i],序列seq2中的某个数a[j]：
- 如果a[i]<a[j],没有逆序数
- 如果a[i]>a[j]，那么逆序数为seq1 中a[i]后边元素的个数(包括a[i])，即len1 -i+1。
3.LeetCode 315. 计算右侧小于当前元素的个数
给你一个整数数组 nums ，按要求返回一个新数组 counts 。数组 counts 有该性质： counts[i] 的值是 nums[i] 右侧小于 nums[i] 的元素的数量。
示例 1：
输入：nums = [5,2,6,1] 输出：[2,1,1,0] 解释： 5 的右侧有 2 个更小的元素 (2 和 1) 2 的右侧仅有 1 个更小的元素 (1) 6 的右侧有 1 个更小的元素 (1) 1 的右侧有 0 个更小的元素
这题和第二题类似，但是这里要解决定位的问题，因为我们的元素节点在归并排序的时候是会移动的，所以需要设置一个索引数组来给这些元素定位。但是求逆序数用的是第二种方法：在前有序数组出列时，计算后有序数组中已经出列的元素个数。
public List<Integer> countSmaller(int[] nums) {
int len = nums.length;
List<Integer> res = new ArrayList<>();
if(len < 2) {
res.add(0);
return res;
}
int[] temp = new int[len];
int[] indexes = new int[len];
int[] result = new int[len];
for(int i = 0; i < len; i++) {
indexes[i] = i;
}
merge(nums, 0, len - 1, temp, indexes, result);
for(int i = 0; i < len; i++) {
res.add(result[i]);
}
return res;
}
public void merge(int[] nums, int left, int right, int[] temp, int[] indexes, int[] result) {
if(left >= right) {
return;
}
int mid = (left + right) >> 1;
merge(nums,left, mid, temp,indexes,result);
merge(nums,mid+1,right,temp,indexes,result);
mergeSort(nums,left,right,mid,temp,indexes,result);
}
public void mergeSort(int[] nums, int left, int right, int mid, int[] temp, int[] indexes, int[] result) {
int i = left;
int j = mid + 1;
for(int t = left; t <= right; t++) {
temp[t] = indexes[t];
}
for(int k = left; k <= right; k++) {
if(i == mid + 1) {
indexes[k] = temp[j++];
} else if(j == right + 1) {
indexes[k] = temp[i++];
result[indexes[k]] += right - mid;
} else if(nums[temp[i]] <= nums[temp[j]]) {
indexes[k] = temp[i++];
result[indexes[k]] += j - mid - 1;
} else {
indexes[k] = temp[j++];
}
}
}
归并排序的思想很重要，在解决负责问题的分治思想有利于将大问题分解。从而更快的解决问题。
