乘积最小问题

乘积最小问题

今天看到三个这样的题

最小乘积生成树,$HNOI2014$画框,不讲武德

大概就是一个物品有两种特征值$a,b$,他的代价是$(\sum a)\times(\sum b)$

$P5540$最小乘积生成树

第一感觉这种题和$wqs$二分有点关系,结果发现没有什么关系...

这种题都是一种套路吧,第一次见的话很难想到

暴力的话就是找出所有生成树求个最小值

考虑求出所有生成树,这个生成树有两个属性$\sum a, \sum b$

我们要找一个二维坐标轴上$(x,y)[Min(x\times y)]$

那么这个东西考虑怎么得到,考场上想到一个东西,能不能分别找两部分的最小值,然后搞一下合并之类的,发现这个思路被合并卡住了,但是对正解有一定启发意义

正解:

$Step1:$

求出与$x/y$轴距离最近的点,也很好找吧,毕竟直接对两个属性分别求一个最小生成树就好了m设两点分别是$A,B$

考虑最优点在哪啊,首先$A\times B$可以看成矩阵面积吧,那么距离原点越近越小

其实把所有点在二维平面上表示出来,最小的必然在下凸壳上,不在下凸壳上必然是不优的

那么又有了$AB,$那么最小值又能进一步确定在$AB$左下方

 

 

 

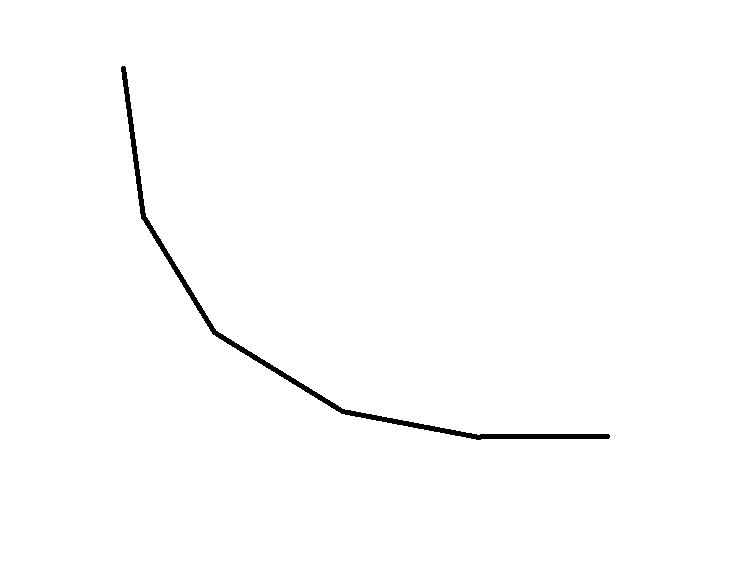
最后维护出来的大概是这个东西

证明,假设最优点在$B$右侧,那么由于斜率增大,感性想一下,一个增大的多,一个减小的少,那么不会更优

或者面积最是$k,y=\frac{k}{x}$,只要我有点脑子就会发现这个必然在里面较优

$Step2:$

找到一个在$AB$左下方距离$AB$最远的点,这个时候还不是最优解,那我们需要找最优解

显然的,最优点必然在直线$AB$靠近原点的一侧,那么就把在这里面的点都搞出来取$\min$就好了(扯)

首先怎么找到距离$AB$左下方最远点(不一定是最优点),最远点就是面积最大的点,因为底边确定

最小化$AB\times AC$即可,首先$A,B$已知

$AB\times AC=(x_B-x_A)y_C+(y_A-y_B)x_C-(x_B-x_A)y_A+(y_B-y_A)x_A$

那么就将前两项最小化就好了(狂暴吐槽洛谷此题第一篇题解),那么把边权设为前面两项的和求一个最小生成树就好了

那么我们可以愉快的认为,我们只需要找到$AB$下面的所有点就好了,至于这个东西可以一步步缩小范围,就是相当于一点一点确定凸包就好了,我们可以根据这个东西找到所有凸包上的点了

$Step3:$

递归处理

$P3236$画框

一样的套路,分别找到第一个最小的和第二个最小的,然后放到二维平面上,然后继续得出一样的式子

这个东西可以搞一个二分图带权最小匹配(小常数费用流可以冲一冲),这道题也就完了

$LOJ3412$不讲武德

如果说前两道题是入门的话,这道题就是$Ex_{Ex_{Ex}}$了

首先可以愉快的$2^n$枚举直接获得$10pts$的优异成绩

这时候前面的题就有用了

枚举$k$,然后找到$k$个元素的两个属性分别最小的不成环集合,然后推式子找到凸壳上的点,这个时候把每个边附上新的权值重新跑一遍,递归处理

这个题就是找到一个新的集合,也是新的式子的最小值,继续递归处理,目前共得到$50pts$

考虑一下刚刚那个重新计算代价的式子

$a_i(r_y-l_y)-b_i(r_x-l_x)$化简式子为$a_i-b_ik$的形式

那么显然每个点$a,b$已知,这个就是一个一次函数的形式,然后这是$m$条直线,至多有$m^2$个交点,那么本质不同的范围只有$m^2$个,直接全处理出来就好了

然而上面的并没有考虑是树还是图,不是树显然就寄了

不是树的话,就考虑最小生成树算法,对于刚才那个是选前$k$个就好了

然而现在不能成环了,还是能搞一个交换关系

那么还是说维护直线交点,这个就是在交点位置维护最小生成树就好了$+15pts$

到了这就是正解了,一些证明就是最小生成树交换次数问题了