模拟费用流
本文主要是对其他博客的理解
分十三类
基本题干\(:\)
\(n\)个松鼠,\(m\)个洞,求一个满足要求的匹配的最小代价
易\(:\)
\(Sit1.\)
只能往左走
考虑每个松鼠尽量走右边第一个就可以,考虑排一下序,每个挑最近的走就可以了
由于一开始看的博客,分两种思路讲
博客:
\(Sit2.\)
无限制,可以左右走
考虑设计\(DP\),\(dp[i][j]\)表示前\(i\)个位置,\(j\)个洞需要匹配
\(j\)可正可负,正表示洞多,负表示鼠多
显然的事情,不交叉匹配一定不会比交叉匹配差,那么转移只用考虑不交叉的情况就可以了,目前转移到第\(i\)个,显然的,负的可以转移到正的,让一个松鼠匹配这个洞可以作为一种方案
显然的一个东西,你可以先把转移的东西塞到\(dp\)状态里面,考虑这样代价计算方式\(:\)
\(|x_i-y_j|\)需要看松鼠和洞的位置具体分析正负
转移方程易得\(:\)
对于松鼠的转移\(:\)
\(j>=0 \ \ \ dp[i][j]=dp[i-1][j+1]+x[i]\)
显然的洞多那么就先把松鼠的位置累积进去,累积进去的也是对的
\(j<0 \ \ \ dp[i][j]=dp[i-1][j+1]-x[i]\)
显然这个时候松鼠多,这个时候转移很有意思,先把洞和松鼠统一排好序之后转移。
显然的事情如果这个时候什么多,他在\(-\)的后面,那么就可以先减去了
对于洞的转移\(:\)
\(j>0 \ \ \ dp[i][j]=min(dp[i-1][j-1]-y[i],dp[i-1][j])\)
这个时候洞多,考虑这个时候加这个洞优让松鼠去匹配优还是让前面的去匹配松鼠比较优
\(j<=0 \ \ \ dp[i][j]=dp[i-1][j-1]+y[i]\)
显然这个时候不交叉匹配让一个松鼠匹配是比较优的
复杂度\(O(n^2)\)
考虑优化这个\(DP\)
刚才写的时候也发现大部分去\(min\)时候不需要的,显然的
优化洞的转移\(:\)
这部分不是很理解,就我理解而言
用了一个栈来存放决策点,每次只需要更新\(f[i][0]\)的答案,其余直接更新即可
至于怎么更新
首先目前如果是松鼠,显然需要让这个松鼠匹配一个洞,那么就在关于洞的栈的决策点挑出一个来更新,感觉不是很对,那么每次\(pop\)是什么,我思考一下.
先考虑这个答案是怎么更新的
\(Ans=tag_2-a[i]+sf.top()\)
\(tag_2\)维护的是所有松鼠位置的\(-\)和所有洞位置的\(+\),。。。(我貌似看的这个博客有问题...)
现将上面小部分略去,博客里代码貌似有点锅
\(upd:\)他的代码解释在下面,枯了。。。(白费半小时伪证,果然证错了)
我们考虑对上面的\(DP\)进行差分处理
\(j>0 \ \ \ d[i][j]=f[i][j]-f[i][j-1]\)
\(j<0 \ \ \ d[i][j]=f[i][j]-f[i][j+1]\)
显然只差分不能表示出每个状态的具体值,只能维护一个相对关系,那么就考虑只存\(f[i][0]\)的值,其他的就可以根据差分数组得到了
得到新的转移方式\(:\)
当前是松鼠
\(f[i][0]=f[i-1][0]+d[i-1][1]+a[i]\)
\(d[i-1][1]=f[i-1][1]-f[i-1][0]\)
\(f[i][0]=f[i-1][0]+f[i-1][1]-f[i-1][0]+a[i]\)
\(f[i][0]=f[i-1][1]+a[i]\)
\(tql!\)
这个\(f[i][0]\)的转移和初始推导式子是一样的。
那么考虑这个时候\(d\)的变化,按原始式子考虑
\(j>=0 \ \ \ dp[i][j]=dp[i-1][j+1]+x[i]\)
\(j<0 \ \ \ dp[i][j]=dp[i-1][j+1]-x[i]\)
目前的差分数组应该和上一层的差分数组数值一样,整体右移一位,\(d[i][j]=d[i-1][j+1]\)
\(j>0||j<-1 \ \ d[i][j]=-d[i-1][1]-x[i]\times 2\)
自然边界和零点位置要特殊考虑
洞的转移\(:\)
\(dp[i][0]=min(dp[i-1][0],dp[i-1][0]+d[i-1][-1]+a[i])\)
\(d[i-1][-1]=dp[i-1][-1]-dp[i-1][0]\)
\(dp[i][0]=min(dp[i-1][0],dp[i-1][0]+dp[i-1][-1]-dp[i-1][0]+a[i])\)
\(dp[i][0]=min(dp[i-1][0],dp[i-1][-1]+a[i])\)
和形式原式一致
关于\(d\)的转移
\(Sit1:d[i-1][-1]+a[i]<0\)
\(dp[i][0]=dp[i-1][0]+d[i-1][-1]+a[i]\)
\(d[i][j]=d[i-1][j-1]\)
\(j>0||j<-1 \ \ d[i][j]=-d[i-1][1]-y[i]\times 2\)
\(Sit2:d[i-1][-1]+a[i]>=0\)
\(dp[i][0]=dp[i-1][0]\)
\(d[i][j]=d[i-1][j]\)
\(j>0||j<-1 \ \ d[i][j]=y[i]\)
写到这,我才明白刚刚的栈维护转移方程的具体含义,泪目了.
其实发现如果是这样转移的话,每次只会更改两个位置的值,其余的都是直接转过来的,那么只需要维护改变位置的值就可以了,复杂度一下子降下来了.
至于上面的转移,我再重新解释一下
代码
stack sz,sf;
int tag1=0,tag2=0,f0=0;
for(int i=1;i<=n;i++)
{
//首先知道,栈维护的是DP方程的差分
if(op[i]==1)//洞
{
tag1-=a[i],tag2+=a[i];
sf.push(f0+a[i]-tag2);
//把差分塞进去,
f0=min(sz.top()+tag1-a[i],f0);sz.pop();
//考虑怎么维护这个f
//我就说第一项没有f0,第二项有f0
//其实考虑交替转移
//假设上一步是鼠
//那这一步的转移式子反带入和初始式子差不太多
//至于tag1和tag2谁明白了给我讲一下,我不是很知道
}
else // 鼠
{
tag1+=a[i],tag2-=a[i];
sz.push(f0+a[i]-tag1);
f0=sf.top()+tag2-a[i];sf.pop();
//原始式子
//f[i][0]=f[i-1][0]+d[i-1][1]+a[i]
//f[i][0]=f[i-1][0]+f[i-1][1]-f[i-1][0]+a[i]
//f[i][0]=f[i-1][1]+a[i]
//这个转移式子
//f0=sf.top()+(yuan)tag2-2*a[i]
}
}
我感觉一上午都在会与不会的边缘游走。。。
发现这个\(DP\)是具有凸性的,也就是说斜率一直呈增长态势,可能会有最低点,或者有可能有最高点。
不对,\(d\)貌似是一直是正数,然后可以解释了,会出现最低点
我找到\(2019WC\)课件了,这时候可以换个思路了
我的理智要溢出来了。
课件:
转移式是大体不变的
只不过对于洞的转移式子
思考一下发现现在把这个放进去一定是优的,然后更正部分式子
\(dp[i][j]=dp[i-1][j-1]+y[i](j<0)\)
\(dp[i][j]=dp[i-1][j-1]-y[i](j>0)\)
\(dp[i][j]=min(dp[i-1][j-1]+y[i],f[i-1][j])(j=0)\)
考虑只有一个点做决策,其余的都是直接转移(位移和整体加\(/\)减)
然后考虑用两个栈来维护\(DP\)的\(j>=0\)和\(j<0\)两个部分,打上整体标记(区间加\(/\)减),然后就可以了。这也就很好的解释了那个代码(上午让我理智溢出的代码)。
至于那个对\(DP\)的差分也就很好理解了
那\(Sit2\)告一段落了
\(Sit3.\)
只能进左边的洞,每个洞有一个代价\(w[j]\),代价是\((x[i]-y[j]+w[j])\),最大化总代价(松鼠不必全部进洞)
转移式子\(:\)
目前是松鼠
\(dp[i][j]=max(dp[i-1][j],dp[i-1][j+1]+x[i])\)
显然你最后一个松鼠给他配对一个是比较优的,然后不需要决策,直接取第二项(这里显然我错了)
目前是洞
\(dp[i][j]=max(dp[i-1][j-1]-y[i]+w[i],dp[i-1][j])\)
貌似多一个洞可能不是很优,目前貌似需要决策
先给出结论,这个\(DP\)维护出来是凸性的
\(dp[i][j]\)表示到了第\(i\)个位置,目前还有\(j\)个洞没有匹配的最大价值
如果\(dp[i][j+1]-dp[i][j]>dp[i][j]-dp[i][j-1]\)
显然的这个时候如果把\(j-1->j\)的多的洞和\(j->j+1\)的洞进行一下替换,这个时候\(dp[i][j]\)是变大的,证明刚才的并不是最优决策,那么上面的式子不成立
那么考虑差分\(dp\)数组
\(d[i][j]=dp[i][j]-dp[i][j-1]\)
上面证明,\(d[i][j]>d[i][j+1]\)
那么这个\(dp\)是先增后降
反观转移式子
\(dp[i][j]=max(dp[i-1][j-1]-y[i]+w[i],dp[i-1][j])\)
这个\(dp\)是凸的,为了保持凸性的方法是,改一个数,其余不变
那么\(d[i-1]\)(上一个位置)到\(d[i]\)也仅仅只是改变一个数
那么理解一下
\(dp[i][j]=max(dp[i-1][j-1]-y[i]+w[i],dp[i-1][j])\)
\(dp[i-1]\)先增后降,转移时,那么考虑在前一部分增得多,后半部分比较优,再往后就是前部分比较优。
中间有个分界点,其余部分按原来的\(d[i-1]\)而这个分界点特殊考虑
貌似这个分界点在最后?
重新看松鼠的转移\(:\)
\(dp[i][j]=max(dp[i-1][j],dp[i-1][i-1][j+1]+x[i])\)
设之前的洞数为\(T\)个
\(dp[i][0]=dp[i-1][0]+d[i-1][1]+x[i]\)
\(dp[i][0]=dp[i-1][0]+dp[i-1][1]-dp[i-1][0]+x[i]\)
\(dp[i][0]=dp[i-1][1]+x[i]\)
显然这样是比较优的
那么显然选第二项是比较优的
\(d[i][j]=d[i-1][j+1](1<=j<T)\)
\(d[i][j]=-x[i](j=T)\)
前面的肯定选第一项,最后一个只能选第二项,目前最后一项和前一项目前差\(x[i]\)
那么转移到第\(i\)个位置,只需要维护\(f[i][0]\)和差分数组\(d\)就可以了
转移的时候只需要\(dp[i][0]\)那么就
\(dp[i][0]=dp[i-1][0]+d[i-1][1]+x[i]\)
查询\(d[i-1][1]\)就可以了
显然的是,证明的\(d\)是单调递减的,那么找一个最大的\(d\)就找到了\(d[i-1][1]\)
那么转移这个方程的时候只需要维护最大值(最大值一定是转移点),支持单点插入(新的点),删除最大值,改变最大值,那么\(priority\)_\(queue\)是个不错的选择
\(Sit3.\)结束了
那么考虑\(Sit2.\)的另外一种解法,费用流
建图也很显然了
起点连向所有松鼠,流量是\(1\),费用是\(0\),然后洞向终点连边,流量是\(1\),费用是\(0\),所有直线上的点向两边的点连边,流量是\(INF\),费用是距离,这样流出来的最小费用最大流,保证每个松鼠都能匹配,并且每个洞最多被匹配一遍,而且得出了正确的结果。
直接费用流时间复杂度不是很优秀
那么考虑模拟费用流
从左到右考虑每一个松鼠,他肯定是匹配目前没有匹配的洞的左右最近的洞的一个。
如果这个时候有一个反向弧\(p->q\),这个时候\(q\)的左边决策点距离会减少\(2\times(q-p)\)
给出结论\(dp\)呈凸性
\(d[i][j]=dp[i][j]-dp[i][j-1](j>0)\)
\(d[i][j]=dp[i][j]-dp[i][j+1](j<0)\)
推导过程和上面类似,为了保证最优,感性理解一下和上面(正确性)也是一致的
如果目前是松鼠
\(dp[i][0]=dp[i-1][0]+d[i-1][1]+x[i]\)
\(dp[i][0]=dp[i-1][0]+dp[i-1][1]-dp[i-1][0]+x[i]\)
\(dp[i][0]=dp[i-1][0]+dp[i-1][1]-dp[i-1][0]+x[i]\)
\(dp[i][0]=dp[i-1][1]+x[i]\)
我写到发现课件写错了(和博客拍一拍==)...
关于\(d\)的转移
\(d[i][j]=d[i-1][j+1]\)
\(j>=0 \ \ \ dp[i][j]=dp[i-1][j+1]+x[i]\)
\(j<0 \ \ \ dp[i][j]=dp[i-1][j+1]-x[i]\)
两边的差分数组不变,中间的发生变化
\(d[i][-1]=-2\times x[i]-d[i-1][1]\)
如果目前是洞
\(dp[i][0]=min(dp[i-1][0],dp[i-1][0]+d[i-1][-1]+y[i])\)
\(dp[i][0]=min(dp[i-1][0],dp[i-1][0]+dp[i-1][-1]-dp[i-1][0]+y[i])\)
\(dp[i][0]=min(dp[i-1][0],dp[i-1][-1]+y[i])\)
如果\(d[i-1][-1]+y[i]<0\)
\(dp[i][0]=dp[i-1][0]+d[i-1][-1]+y[i]\)
否则
\(dp[i][0]=dp[i-1][0]\)
由于\(dp\)转移如下,只有\(j=0\)时候\(d\)不同
\(dp[i][j]=dp[i-1][j-1]+y[i](j<0)\)
\(dp[i][j]=dp[i-1][j-1]-y[i](j>0)\)
\(dp[i][j]=min(dp[i-1][j-1]+y[i],f[i-1][j])(j=0)\)
那么\(d\)
\(d[i][j]=d[i-1][j-1](j<0||j>1)\)
\(j=1\)
\(dp[i][1]=dp[i-1][0]-y[i]\)
第一个式子\(d[i][1]=-2\times y[i]-d[i-1][-1]\)
第二个式子\(d[i][1]=-y[i]\)
每次只需要一个点决策,其余的点直接转移
那么\(d\)还是一个单调的,最高点应该在\(dp[i][0]\)处去到
还是考虑用\(heap\)维护转移,然后我们使用\(d\)转移\(dp[0]\),然后用上一个\(dp[0]\)去更新\(d\)
伪代码
我们用\(heap\)去转移\(dp\),本质上是反悔贪心的过程
相当于维护了两个增广集合,分别代表松鼠的增光或者洞的增广,还是说,按照刚才说的直接建立费用流跑图,和这个的处理方式是相同的,无非是改变之后对距离的增减之类,更是对于决策点更新与维护
其实我感觉是转移\(dp\)好理解点
\(Sit4.\)
进度条刚过半,请放心食用
每个洞可容纳多只老鼠,有一个容量上限
先说点乱搞能过的做法\(/xyx\)
做两遍贪心,强制每只松鼠的运动方向
求得答案\(S_1/S_2\)
首先给出结论\(:\)
对于原问题,一定存在最优解属于\(min(S_1+S_2,V)\)里面
\(V\)是初始洞的集合
感性理解一下,就是部分拼成整体,肯定他的选择,是从这个里面挑出部分来拼到一起的最优解。
那么我们对于得到的洞(拆开)跑一遍\(Sit2.\)我只能说太妙了\(!\)
自然模拟费用流是能解决掉此问题的
考虑模拟费用流是怎么处理的
每次到一个点,考虑对对它进行增广,就是在所有选择里面挑一个代价最小的更新答案,相当于贪心,然而贪心会挤掉其他选择,自然把代价同样压入\(pq\),在所有选择挑出最优决策即可
对于一个洞能多次使用,就把他拆成好多洞就可以了
具体和上面的实现差不多
\(Sit5\)
每只松鼠可以任意分身多次,每只洞容量无限,每只松鼠至少一个分身进洞,一个洞至少有一只松鼠
考虑把一只松鼠拆成两类
第一种是容量是\(1\),费用是\(-INF\)
第二种是容量是\(INF\),费用是\(0\)
同样的洞按照\(Sit4\)的做法,把上限改成\(INF\)即可
讲到这就差不多了,下面的都是一些加强版,我先写几道题加深一下理解再去补充
\(4977. [Lydsy1708\)月赛\(]\)跳伞求生
代码
#include<bits/stdc++.h>
#define int long long
#define MAXN 550000
using namespace std;
struct node
{
int id,zd,val;
}poz[MAXN];
bool cmp(node x,node y)
{
if(x.zd!=y.zd)
{
return x.zd<y.zd;
}
return x.id<y.id;
}
int Ans,n,m;
priority_queue<int>res;
signed main()
{
//这不就是只能往左选择吗
//显然的如果是房子就插入pq
//如果是人就开始决策
//从小到大排序
//很显然的事情,如果还有的话直接选
//唯有冲突的时候才会选一个大的
freopen("T1.in","r",stdin);
freopen("T1.out","w",stdout);
scanf("%lld%lld",&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%lld",&poz[i].zd);
poz[i].id=0;
}
for(int i=1;i<=m;i++)
{
scanf("%lld%lld",&poz[i+n].zd,&poz[i+n].val);
poz[i+n].id=1;
}
sort(poz+1,poz+1+n+m,cmp);
for(int i=1;i<=n+m;i++)
{
if(poz[i].id==0)
{
if(res.empty()) continue;
if(poz[i].zd+res.top()<0) continue;
Ans+=poz[i].zd+res.top();
res.pop();
res.push(-poz[i].zd);
}
else
{
res.push(-poz[i].zd+poz[i].val);
}
}
cout<<Ans<<endl;
}
感觉很像后悔贪心,但确实是退流的思想
例\(2\ NOI2017\)蔬菜
貌似做着题突然发现,模拟费用流好像就是后悔贪心...貌似高一时接触到就一直叫后悔贪心\(?\)
还是考虑这道题,我做的后悔贪心的题都有一种普遍的思路,倒推思想,正推需要考虑的事情太多,不如倒推解决。
考虑倒推的现象,就是从某一天开始,每天出现\(x\)个某种蔬菜,然后选择逐渐变多,每次找最优解即可
考虑为什么能解决问题,首先这题有一个限制,就是每天有蔬菜消失,但是前一天如果卖的足够多就不会消失,考虑这个怎么解决,这个用每个蔬菜每天增加一定量能否解决,对啊,这个的本质是什么,就是他限制了了你的售卖天数,否则在某个前缀和里面,最多可以卖一个数量,想到这我觉得已经很妙了,继续考虑这一天能不能卖多点,你只是增加了蔬菜,可以在前面某一天卖出去,那么就很显然了
我们现在就可以的得到第\(p\)天的答案,往前推也不是很难,只需要把今天收益最小的一部分删去即可
事到如今,我只能说模拟费用流\(yyds\)
\(tql,sto,orz\)
代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN=100000;
struct node
{
int a,s,c,x;
}poz[MAXN+10];
int n,m,k,Ans[MAXN+1000];
priority_queue<pair<int,int> >Q;
pair<int,int>S[MAXN+1000];
bool vis[MAXN+1000];
int used[MAXN+1000];
vector<int>de[MAXN+1000];
signed main()
{
scanf("%lld%lld%lld",&n,&m,&k);
for(int i=1;i<=n;i++)
{
scanf("%lld%lld%lld%lld",&poz[i].a,&poz[i].s,&poz[i].c,&poz[i].x);
// cout<<"now: "<<i<<endl;
}//输入收益,第一次奖励,库存,腐败程度
for(int i=1;i<=n;i++)//最后一次出现时间
{
if(poz[i].x==0)
{
de[MAXN].push_back(i);
}
else
{
de[min(MAXN,(poz[i].c+poz[i].x-1)/poz[i].x)].push_back(i);
}
}
for(int i=MAXN;i>0;i--)
{
//属于是经典倒推了
//枚举今天是第几天
int top=0;
for(int j=0;j<de[i].size();j++)
{
Q.push(make_pair(poz[de[i][j]].a+poz[de[i][j]].s,de[i][j]));
}
//放入决策点(价值,编号)
//这里价值直接放进去了单位收益和起始奖励
if(Q.empty()) continue;
for(int j=m;j&&!Q.empty();)
{
//选出m个点
//vis用处尚且不清楚
int val=Q.top().first;
int id=Q.top().second;
Q.pop();
if(!vis[id])
{
vis[id]=true;
//used是这个编号的蔬菜用了几个
//j是还需选多少个
Ans[MAXN]+=val;
used[id]+=1;
j--;
if(poz[id].c>1) Q.push(make_pair(poz[id].a,id));
//好像是用没用过
//考虑这个算法貌似不用保证什么退流之类的???
//c是库存,表示还能继续用但是不用计算第一次多的奖励了
//这里貌似有点意思,处理的仅仅是第一次的奖励+贡献
//那么这样是对的吗,先往下看
}
else
{
int res=min(j,poz[id].c-used[id]-(i-1)*poz[id].x);
//.......我貌似忘记used了
//rest记录的是目前节点能够选几个
j-=res;
//剩余还有几个
used[id]+=res;
//记录使用的个数
Ans[MAXN]+=(res*val);
//显然是对的
if(used[id]!=poz[id].c) S[++top]=(make_pair(poz[id].a,id));
}
}
//我现在好奇一件事,就是说你这个东西的第一次奖励在最后一次算是合法的吗
//考虑这样能不能保证每一天是最多的,发现好像是只需要每一天的最大值就可以了
//那这样既保证了选择是合法的,也保证了最多,貌似是没有问题的
//这样是否和结果的最优决策一样
//考虑必然是选那些最优点没错,我无非是把一些从后面统计的贡献转到前面了
//反正都是最大值那就没错了
while(top) Q.push(S[top--]);
}
while(!Q.empty()) Q.pop();
//我现在悟了...
//又不明白了...
//我在考虑正推能不能解决问题
//好像不太行的样子
//正推没有办法解决腐烂问题
//而倒退相当于重新模拟一遍
//正确性也是对的
//但是这个第一次的收益呢
//那没事了,我懂了
int Sum=0;
for(int i=1;i<=n;i++)
{
Sum+=used[i];
}
for(int i=1;i<=n;i++)
{
if(used[i]==1) Q.push(make_pair(-poz[i].a-poz[i].s,i));
else if(used[i]) Q.push(make_pair(-poz[i].a,i));
}
for(int i=MAXN-1;i>0;i--)
{
Ans[i]=Ans[i+1];
while(Sum>i*m&&!Q.empty())
{
//这必然需要这一步选的恰好差不多多
int val=Q.top().first;
int id=Q.top().second;
Q.pop();
if(used[id]>1)
{
int rest=min(used[id]-1,Sum-(i*m));
Ans[i]+=rest*val;
used[id]-=rest;
Sum-=rest;
if(used[id]==1) Q.push(make_pair(-poz[id].a-poz[id].s,id));
else Q.push(make_pair(-poz[id].a,id));
}
else
{
Ans[i]+=val;
used[id]-=1;
Sum-=1;
}
}
}
int p;
for(int i=1;i<=k;i++)
{
scanf("%lld",&p);
cout<<Ans[p]<<endl;
}
}
最后一道例题
\(P5470 [NOI2019]\) 序列
这个思路很妙啊
首先建出费用流的模型,原点向所有\(A\)中的点连边,流量是\(1\),费用是\(val_a[i]\),\(A\)和\(B\)中的点一一对应连边,流量是\(1\),费用是\(0\),然后考虑汇点和所有\(B\)连边,流量是\(1\),费用是\(val_b[i]\),然后这个时候只有满足相等的边,那么不等的边,建两个虚点,流量是\(k-l\),费用是\(0\)
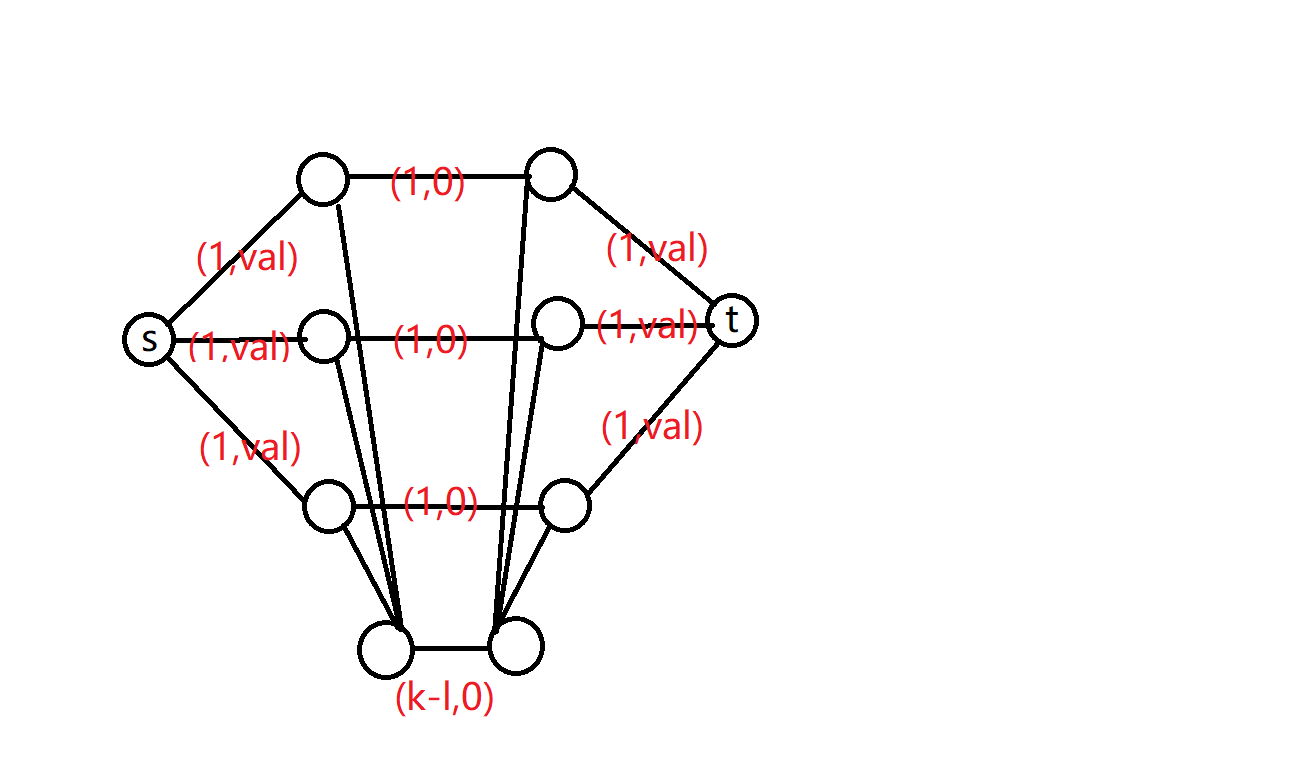
这个图流量为\(k\)的最大费用最大流就是答案
考虑正确性,首先选了\(2\times k\)个点
最多有\(k-l\)对不同,而且价值最大
考虑什么时候得到最大解
显然的事情,每组里面最大的\(k-l\)个必选
然后剩下的搞一个匹配即可
我觉得我可以自己写写?
写着写着发现要维护好多东西,我再想想

