欧拉角、万向节死锁（锁死）理解

目录

• 欧拉角理解
  • 举例讲解
  • 顺规、内旋与外旋
    • 顺规
    • 内旋与外旋
    • 总结
  • 东北天坐标系
  • 数学表示
    • 公式推导
    • 举例计算
• 万向节死锁理解
  • 说明
  • 形象表示
  • 数学表示

欧拉角理解

---

举例讲解

欧拉角用三次独立的绕确定的轴旋转角度来表示姿态。如下图所示

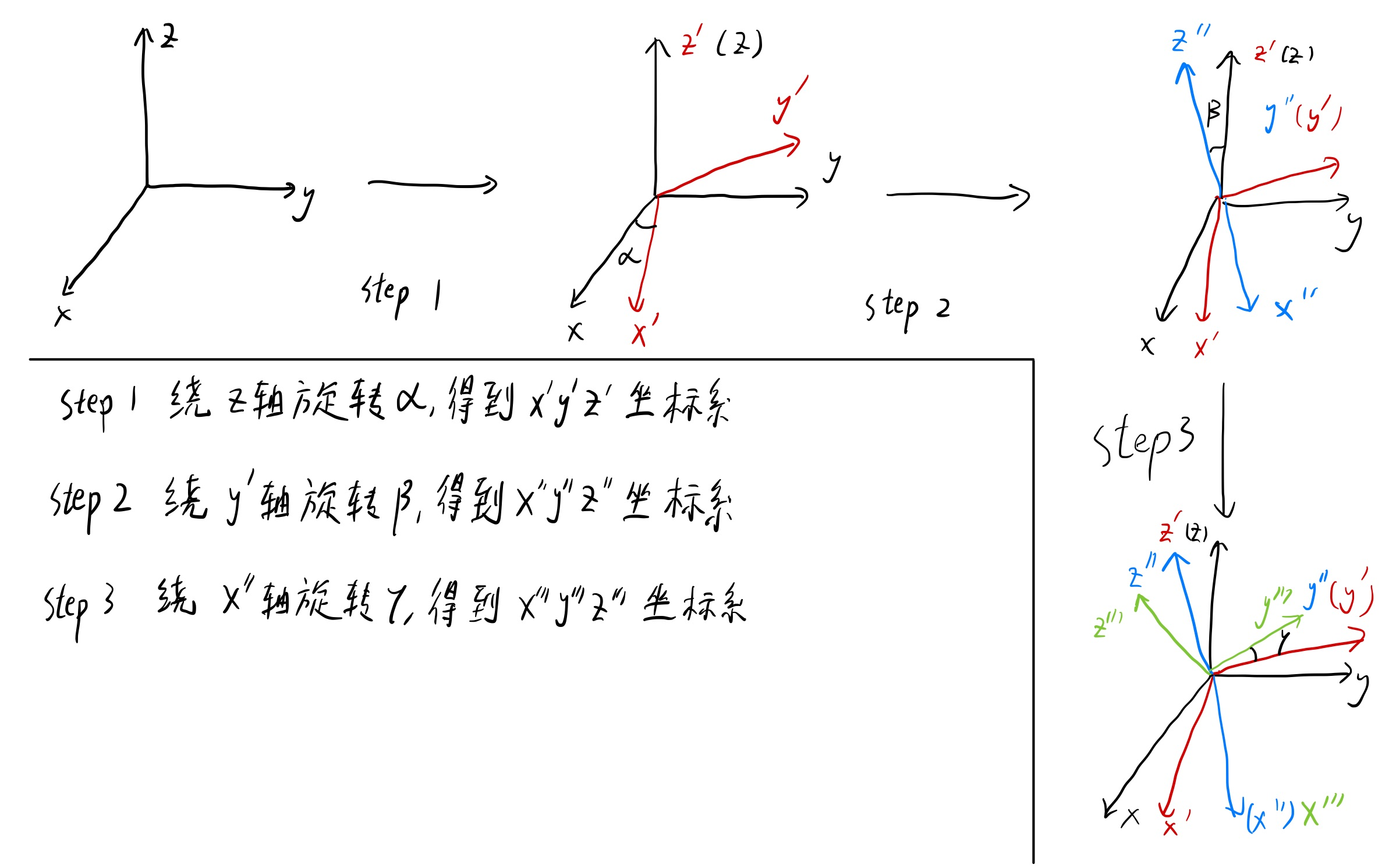
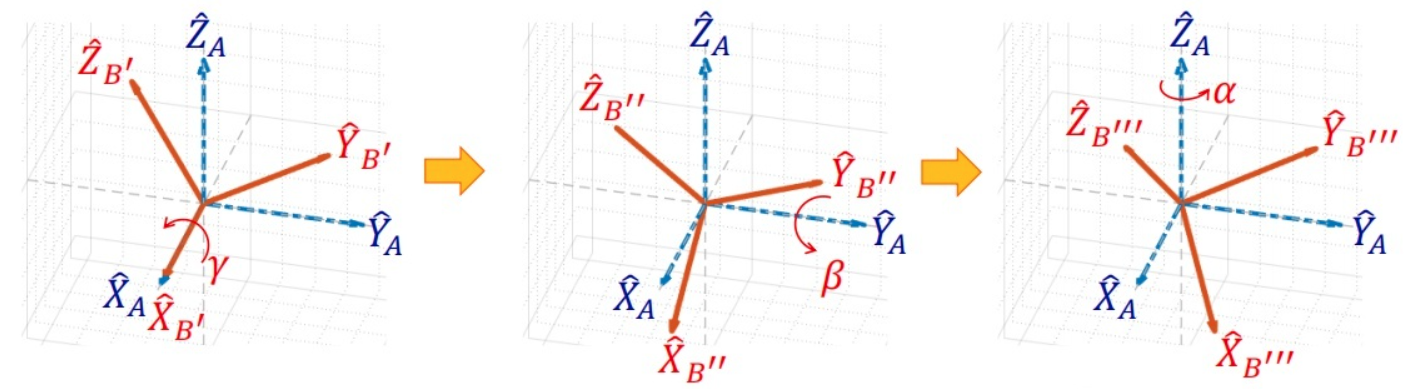
经过三次旋转，旋转角度分别为\(\alpha\)、\(\beta\) 和 \(\gamma\)，由初始的\(xyz\)坐标系得到了最终的\(x'''y'''z'''\)坐标系。这就是欧拉角来表示姿态的方法。

如图所示为航空航天中常用的欧拉角，图中的\(\psi\)、\(\theta\)和\(\phi\) 对应于上图中的\(\alpha\)、\(\beta\) 和 \(\gamma\)。

航空航天中常用的欧拉角

---

顺规、内旋与外旋

上面所举的例子中，旋转的顺序是按照 \(z-y-x\) 的顺序来进行旋转的，并且每一次旋转都是绕自身轴（运动轴）进行的， 这只是欧拉角的一种表示方式。欧拉角共有12种表示方式。

顺规

顺规即欧拉角三次转动的顺序规定，欧拉角一共有12种顺规

三个轴只用两个的：Proper Euler angles (z−x−z, x−y−x, y−z−y, z−y−z, x−z−x, y−x−y）
三个轴全都用的：Tait-Bryan angles (x−y−z, y−z−x, z−x−y, x−z−y, z−y−x, y−x−z）

上文举例所用的 \(z-y-x\) 是三个轴都用的一种顺规，即 先绕\(z\)轴旋转，再绕\(y\)轴旋转，最后绕\(x\)轴旋转。

内旋与外旋

根据绕旋转轴的不同，可以分为内旋和外旋。

内旋 Intrinsic rotations：绕运动轴
外旋 Extrinsic rotations：绕固定轴

上文所举的例子每次旋转都是绕上一次旋转所新产生的坐标轴旋转的（这句话有点绕），比如第二次旋转绕的是\(y''\)而不是固定的坐标轴\(y\)。所以是绕运动轴，即内旋。

• 如下图所示，每一次旋转都是绕蓝色的固定轴旋转

绕固定坐标轴旋转

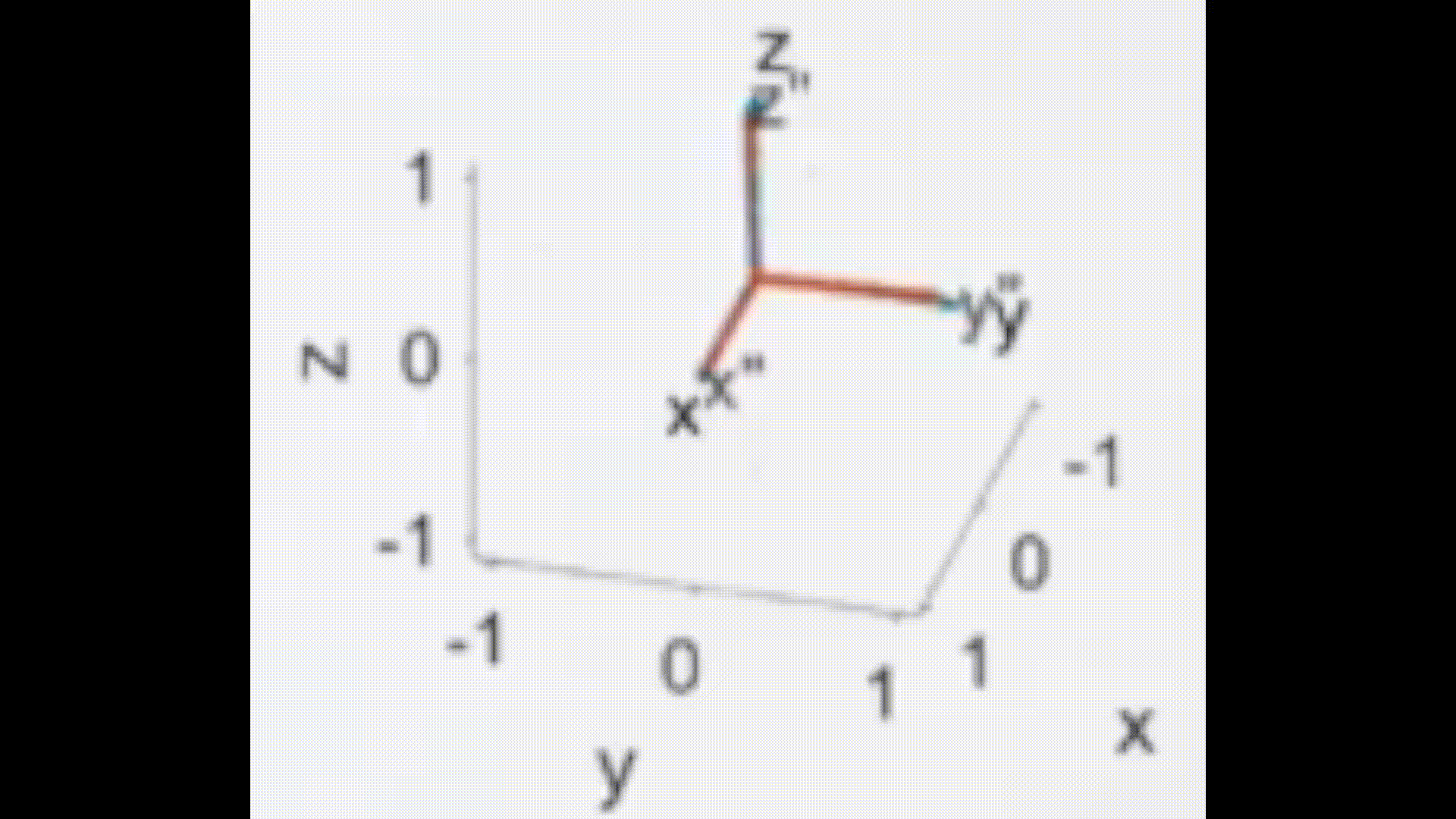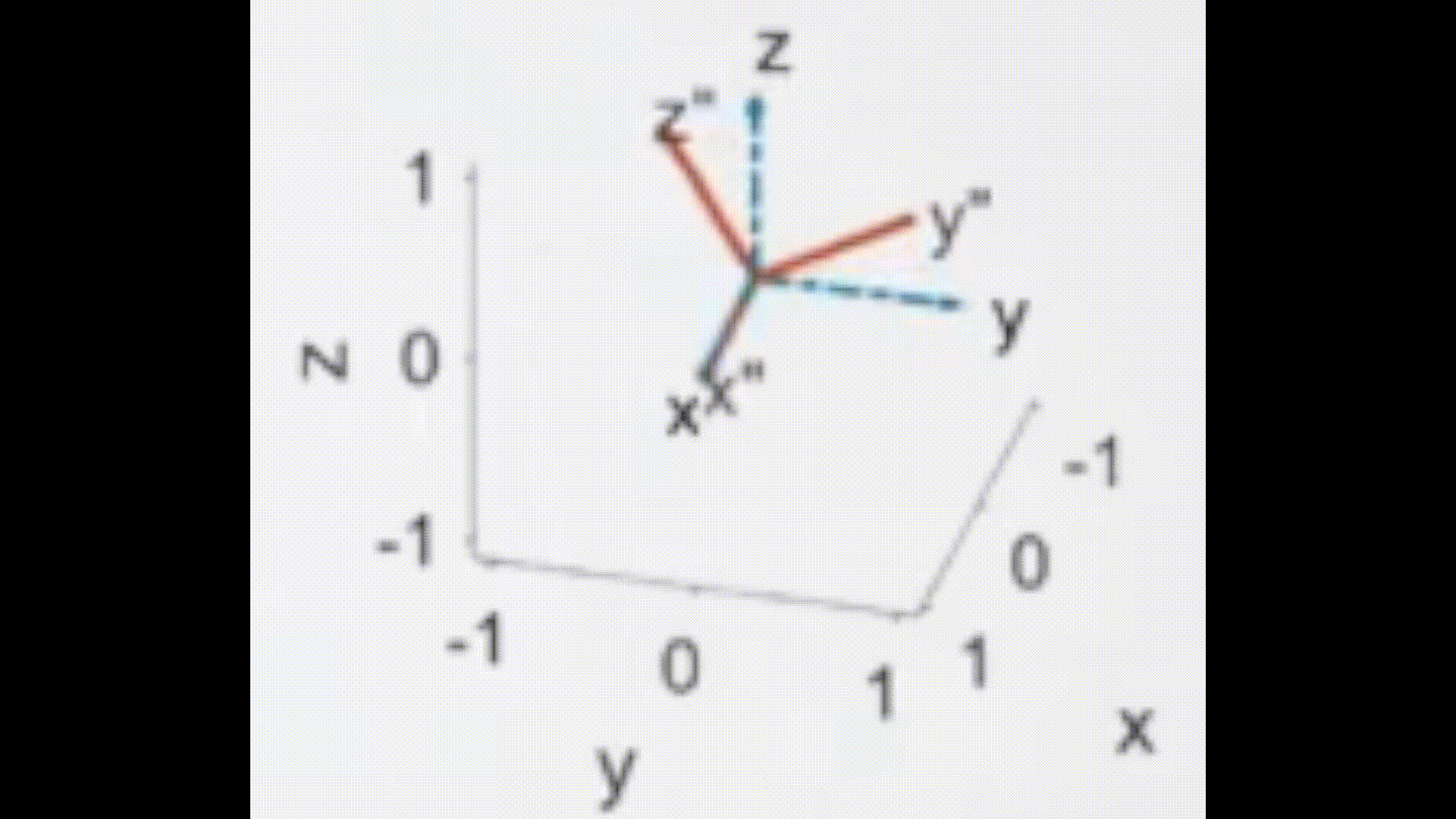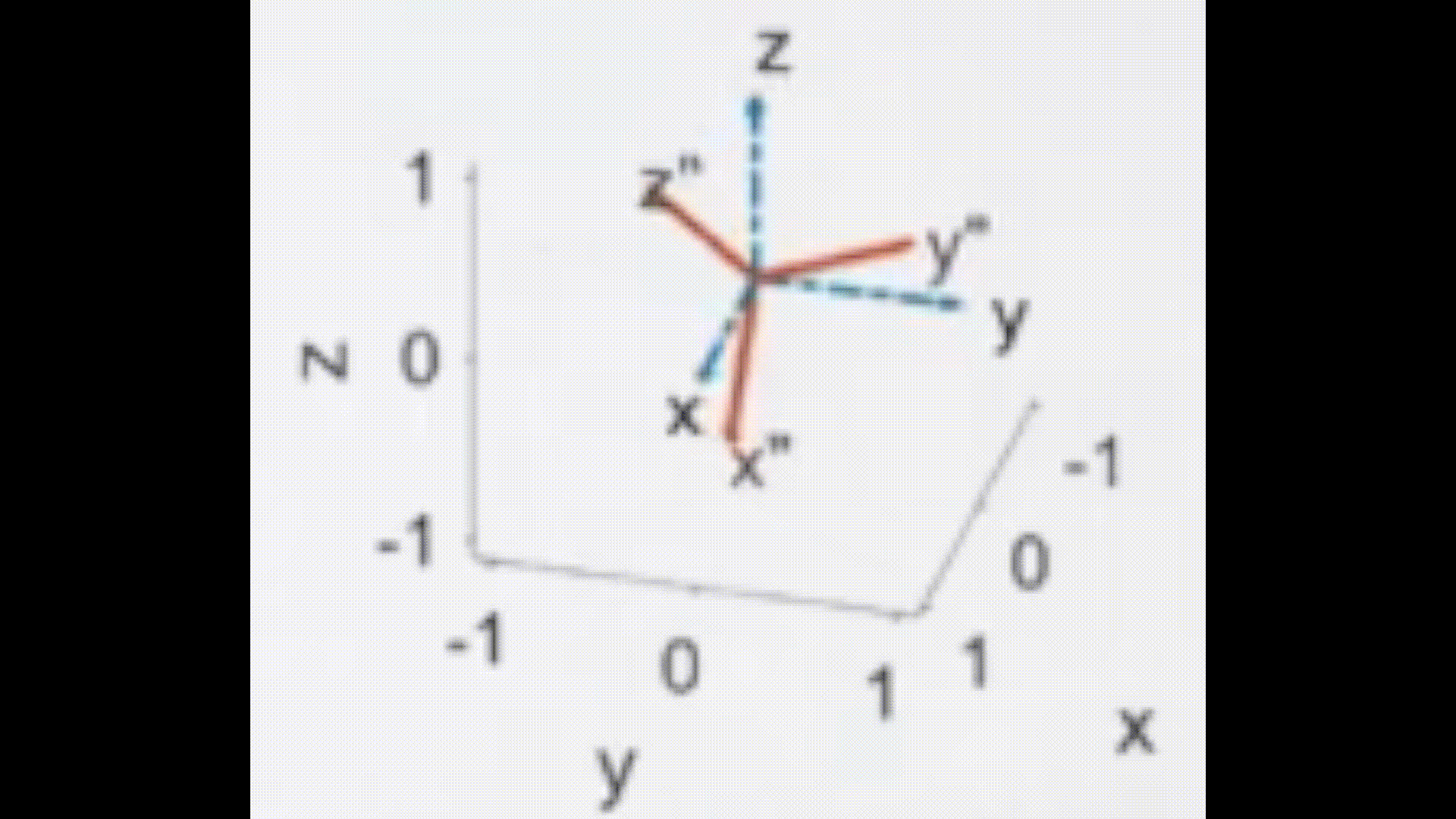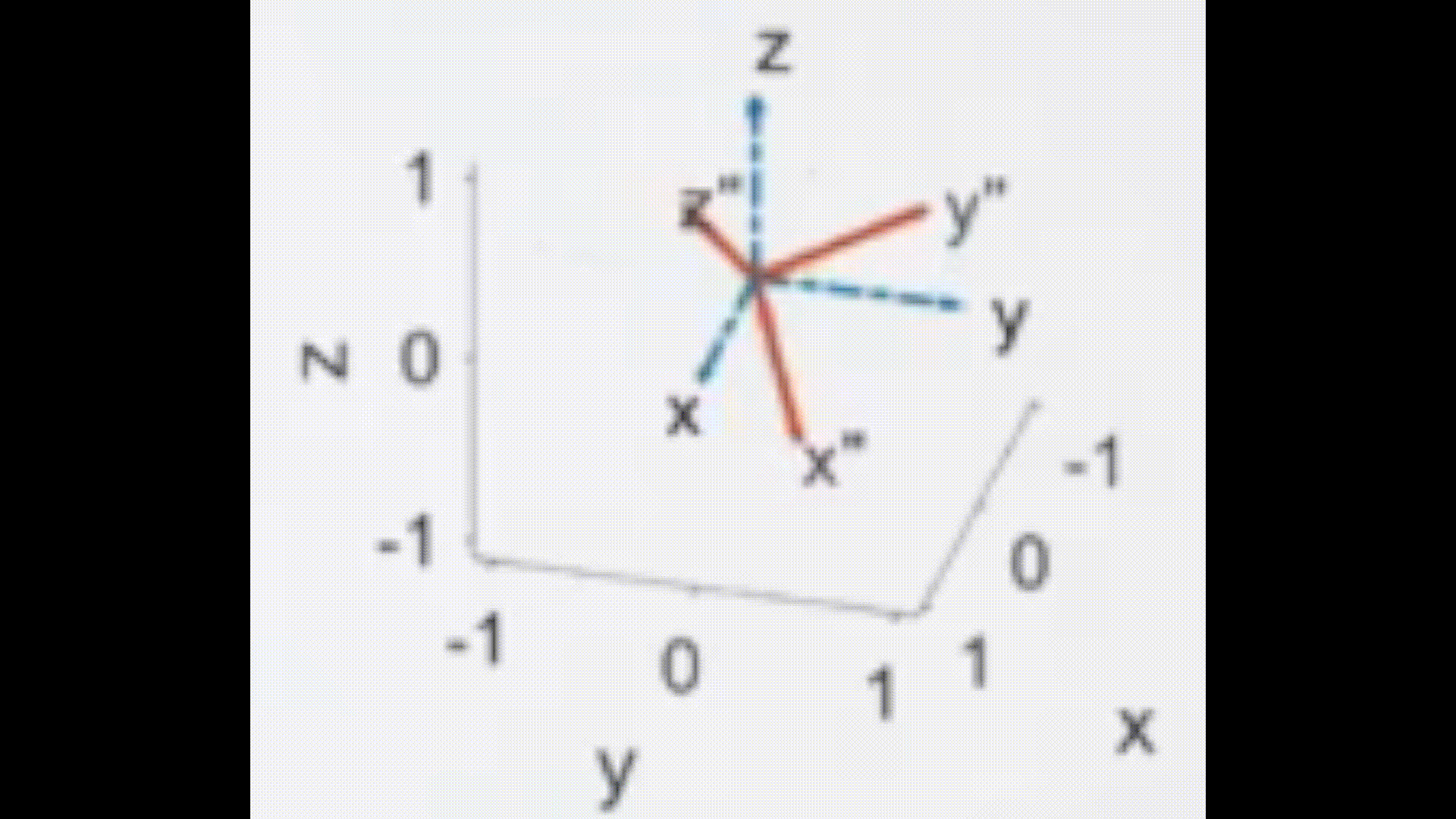
• 如下图所示，每一次旋转都是绕红色（第一张图）、绿色（第二张图）、紫色（第三张图）的运动轴旋转

绕运动坐标轴旋转

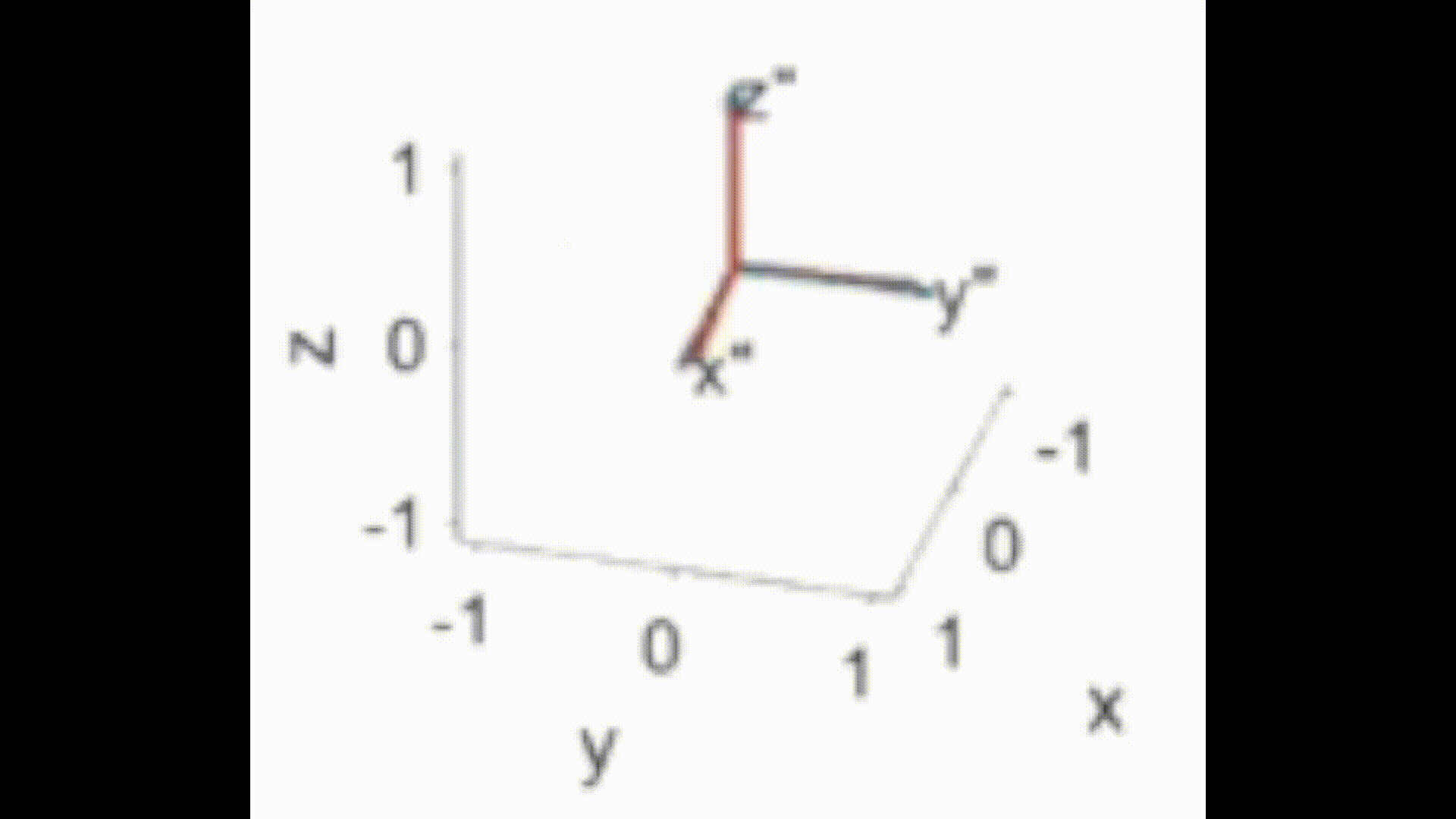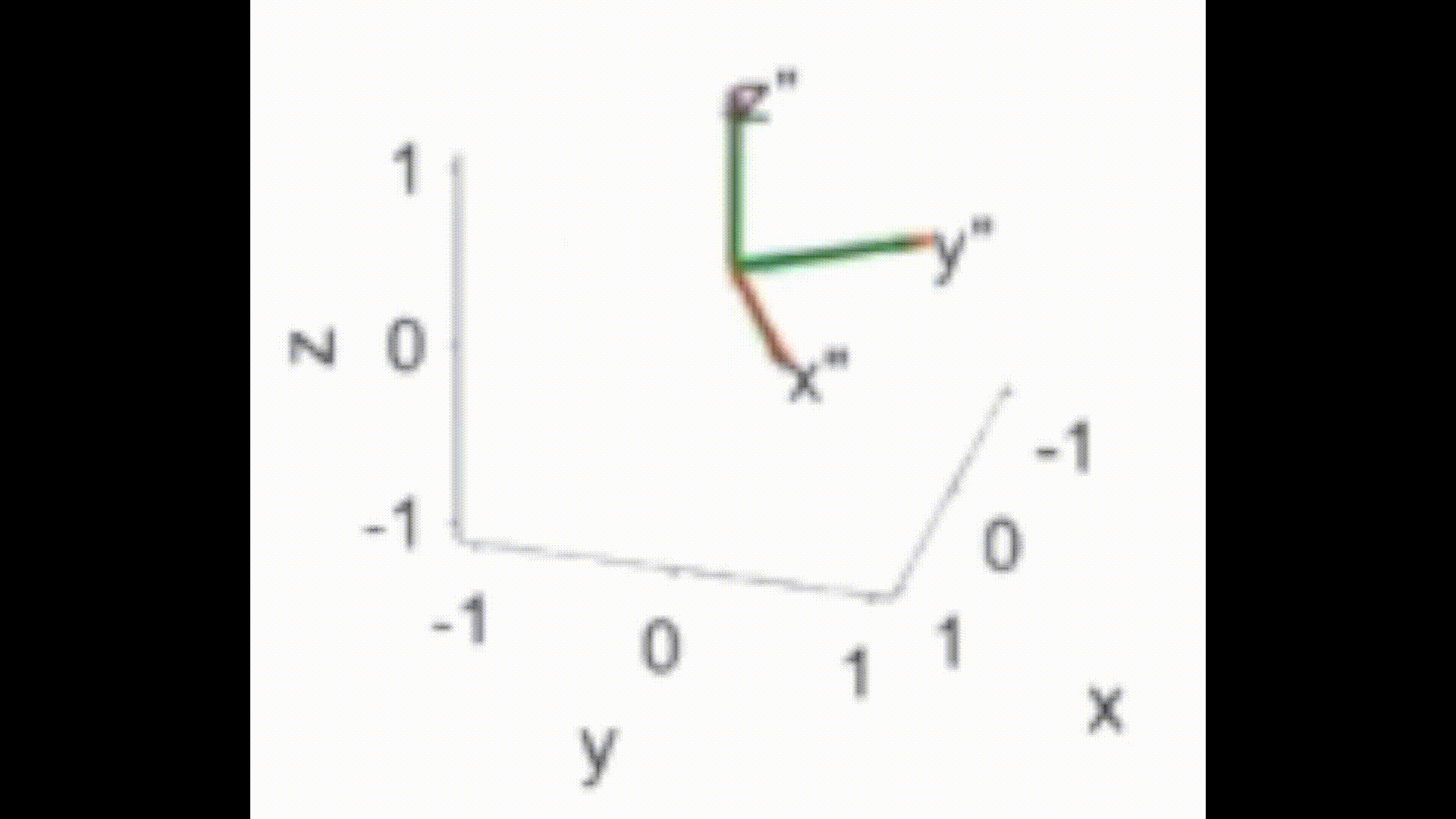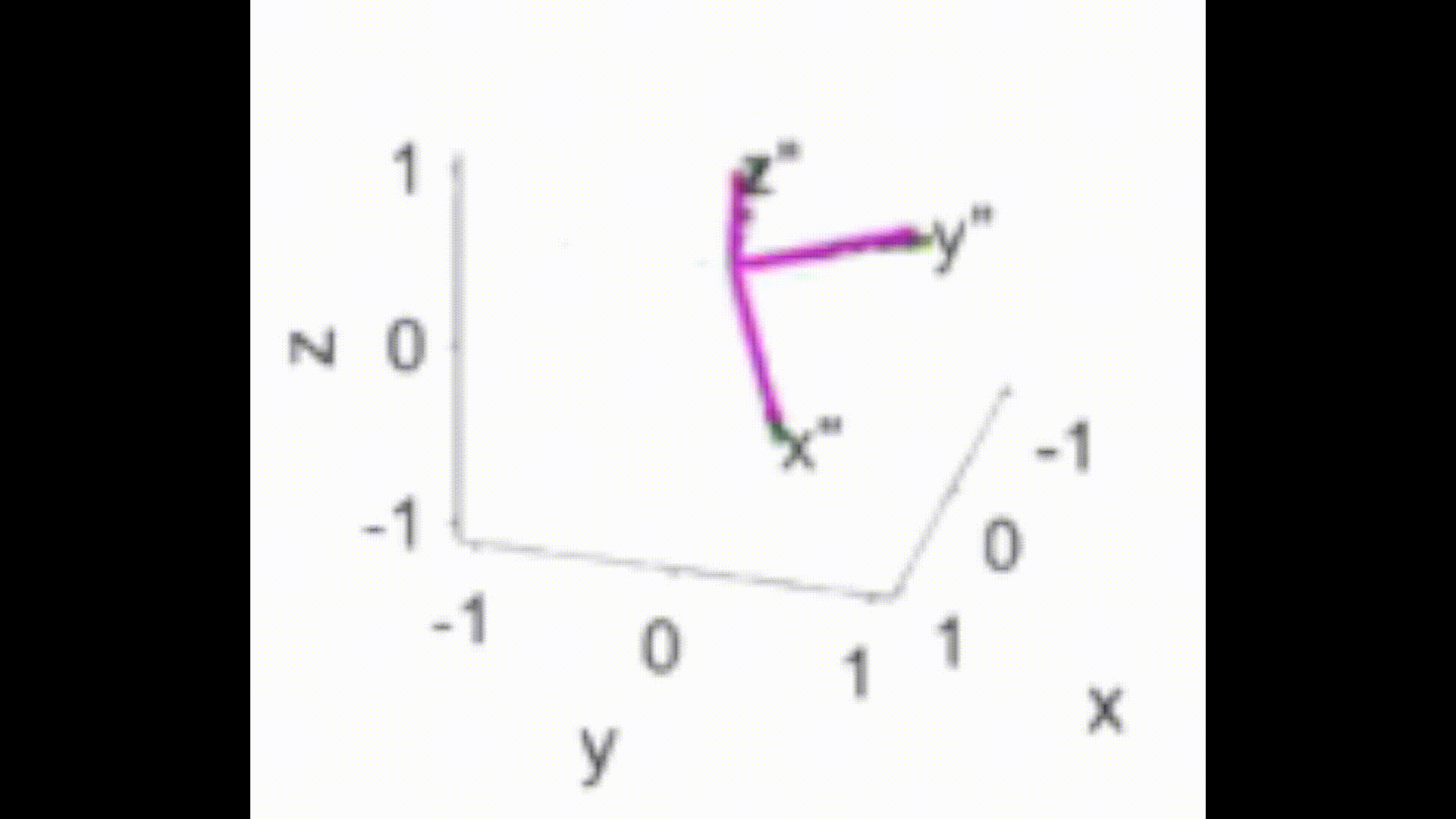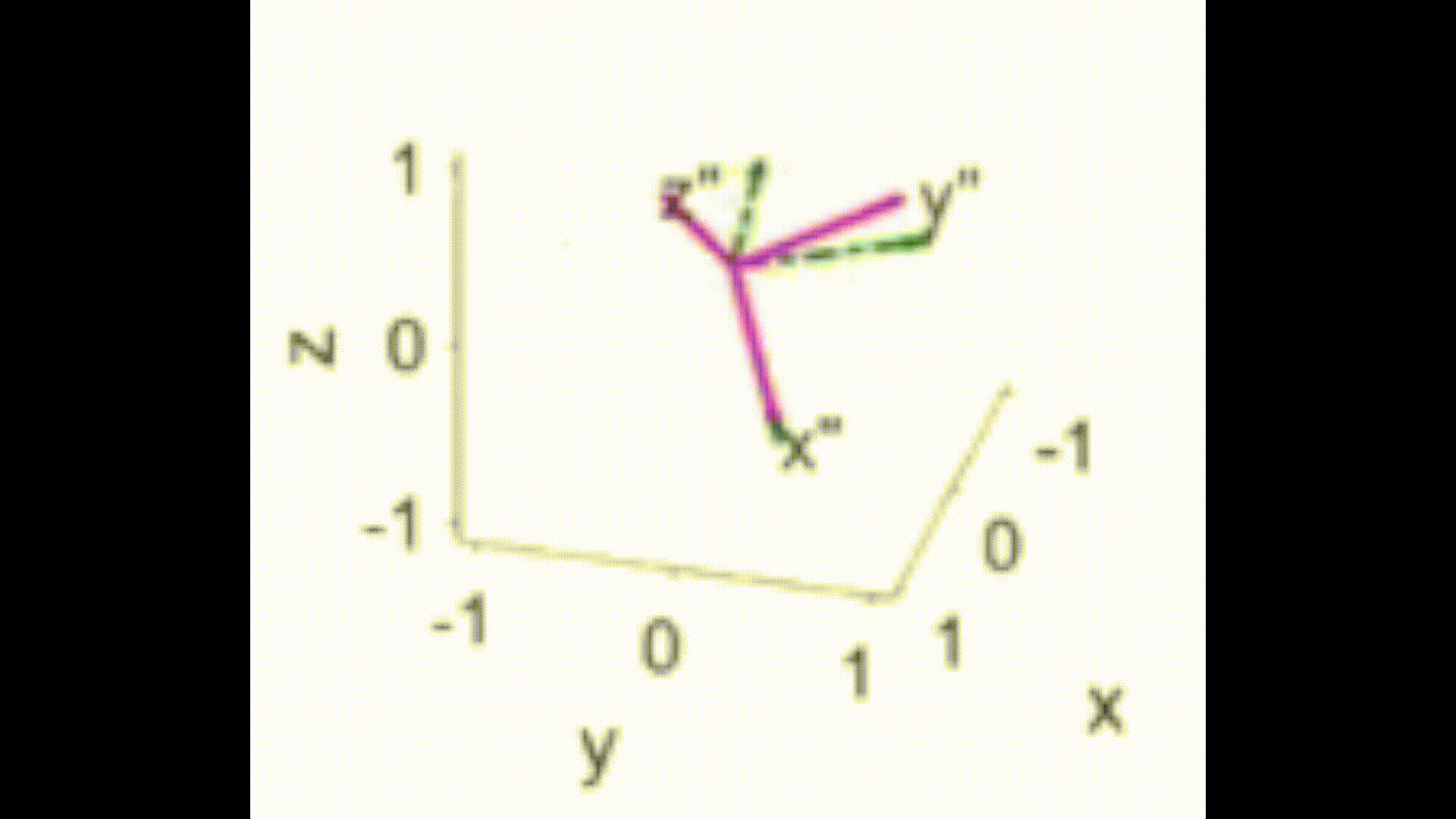
这里图片应引用了台大林沛群老师讲解的机器人运动学。

在绕轴旋转的时候，顺规有12种，内外旋有2种，但是一般情况下，欧拉角都是说的绕自身轴（运动轴）旋转，即 内旋 。所以欧拉角共有 \(1\times12=12\) 种表示方式。

---

总结

首先说一个很有意思却很不直观的结论：三次绕固定轴旋转的最终姿态和以相反顺序三次绕运动轴旋转的最终姿态相同。

一般情况下，每一个领域有自己默认的欧拉角定义，也就是24种的其中之一。比如经典力学中使用\(zxz\)，量子力学使用的是\(zyz\)，航空航天使用\(zyx\)或\(zxy\)。所以在跨行业或者跨模块协作的时候，一定要问清楚对方是哪一种欧拉角。

---

东北天坐标系

我在调一款九轴姿态传感器的时候，看到这样的表述：

这里面东北天坐标系是指，旋转前的\(xyz\)坐标轴与东北天这三个方向是对应的，即\(x\)轴指向东方，\(y\)轴指向北方，\(z\)轴指向天空。
或者这么理解：当计算出的欧拉角的 \(\alpha=0,\beta=0,\gamma=0\) 的时候，\(x\)轴指向东方，\(y\)轴指向北方，\(z\)轴指向天空。如下图所示

---

数学表示

公式推导

以 \(z-y-x\) 顺规和绕自身轴（运动轴）旋转为例，介绍一下欧拉角与旋转矩阵的关系。
规定：
先绕 \(z\) 轴旋转 \(\alpha\) ； 再绕 \(y\) 轴旋转 \(\beta\) ； 再绕 \(x\) 轴旋转 \(\gamma\)
用 \(c\) 表示 \(cos\) ，用 \(s\) 表示 \(sin\)

绕 \(z\) 轴旋转 \(\alpha\) 所产生的旋转矩阵为

\[R_1=\begin{bmatrix} c\alpha & -s\alpha & 0 \\ s\alpha & c\alpha & 0 \\ 0 & 0 & 1 \end{bmatrix} \]

绕 \(y\) 轴旋转 \(\beta\) 所产生的旋转矩阵为

\[R_2=\begin{bmatrix} c\beta & 0 & s\beta \\ 0 & 1 & 0 \\ -s\beta & 0 & c\beta \end{bmatrix} \]

绕 \(x\) 轴旋转 \(\gamma\) 所产生的旋转矩阵为

\[R_3=\begin{bmatrix} 1 & 0 & 0 \\ 0 & c\gamma & -s\gamma \\ 0 & s\gamma & c\gamma \end{bmatrix} \]

绕自身轴（运动轴）转动时，先转动的放在前面，求得旋转矩阵为

\[\begin{aligned} R_{ZYX} &=R_1 R_2 R_3 \\ &=\begin{bmatrix} c\alpha c\beta & c\alpha s\beta s\gamma - c\gamma s\alpha& s\alpha s\gamma + c\alpha c\gamma s\beta \\ c\beta s\alpha & c\alpha c\gamma + s\alpha s\beta s\gamma & c\gamma s\alpha s\beta - c\alpha s\gamma \\ -s\beta & c\beta s\gamma & c\beta c\gamma \end{bmatrix} \end{aligned}\]

举例计算

假设先对 \(z\) 轴旋转 \(45°\) ，再对 \(y\) 轴旋转 \(30°\) ，最后对 \(x\) 轴旋转 \(60°\)

计算得到最终结果为

\[\begin{aligned} R_{ZYX} &=R_1 R_2 R_3 \\ &=\begin{bmatrix} 0.6124 & 0.3062 & 0.1768 \\ 0.6124 & 0.6597 & 0.1768 \\ 0 & 0.75 & 0.4330 \end{bmatrix} \end{aligned}\]

---

万向节死锁理解

说明

欧拉角表示姿态的时候，会出现万向节死锁的情况
当我使用传感器（维特智能WT901c-485）读取角度的时候，在\(ZYX\)的顺规下，当pitch角度为90或-90的时候，roll和yaw角度会乱飘，这就是遇到了万向节的死锁。
不同的顺规死锁的情况不一样，本文仅以\(ZYX\)说明死锁的情况。

---

形象表示

我们以手机为例，说明一下万向节死锁的情况

注意，欧拉角表示姿态时，只能旋转三次，这是理解死锁的前提！

首先这是一个手机，我们对其建立坐标系，平行于手机长边是 \(X\) 轴，平行于手机短边是 \(Y\) 轴，垂直于桌面是 \(Z\) 轴。我们按照 \(ZYX\) 的顺规，对手机进行旋转

1. 首先，先绕 \(Z\) 轴旋转得到 \(X'Y'Z'\) 坐标系，如图中绿色所示

2. 然后对 \(X'Y'Z'\) 绕 \(Y'\) 轴旋转-90°，得到 \(X''Y''Z''\) ，如图中蓝色所示（此时旋转后的 \(X''\) 轴与旋转之前的 \(Z'\) 轴重合）

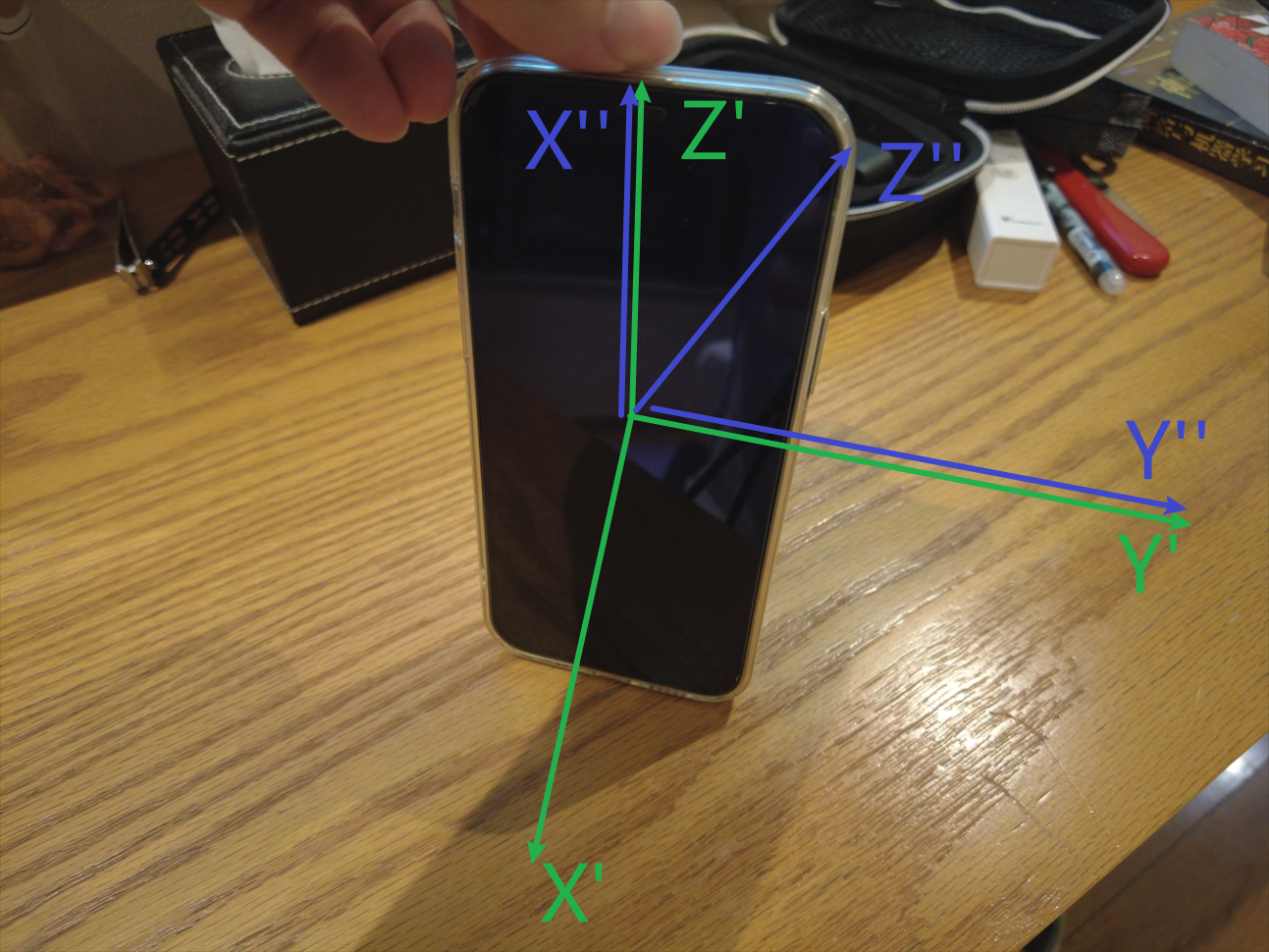
3. 最后将 \(X''Y''Z''\) 绕 \(X''\) 轴旋转得到 \(X'''Y'''Z'''\) 坐标系，如图中黄色所示。

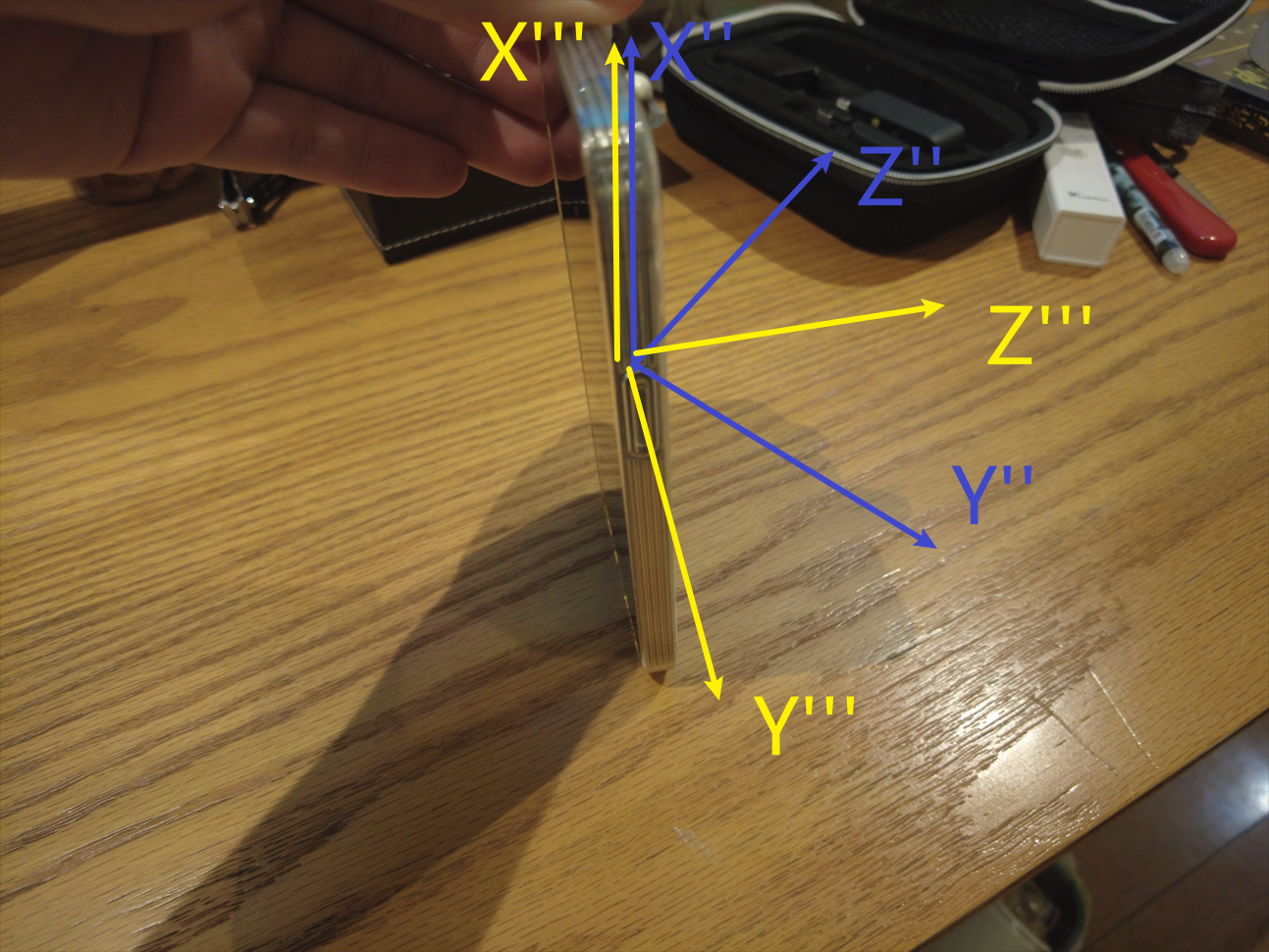
这时候重点来了！！！

我们发现，这样旋转过后，手机的长边是与桌面（地面）垂直的，手机的短边是与桌面（地面）平行的。并且，无论第一步转 \(Z\) 轴转了多少度，第三步转 \(X\) 轴转了多少度，手机长边与短边都是这个状态。

这就是欧拉角表示角度时的“万向节死锁”现象，按理说欧拉角可以表示三个自由度，即三个方向的旋转。但是在这种情况下，只要\(\beta=\pm90°\)，无论 \(\alpha\)与\(\gamma\)怎么取值，手机最终的长边都会与地面垂直，这就好像少了一个自由度，只有2个自由度，所以称之为“万向节死锁”。

那么为什么会出现这种情况呢？

一种感性的理解是这样：我们在第二步旋转的时候，将旋转后的 \(X''\) 轴与旋转之前的 \(Z'\) 轴重合（这个我在上面旋转演示的时候加粗说明了）。

而第一步旋转是绕 \(Z'\) 轴旋转的，第三步旋转是绕 \(X''\) 轴旋转的，所以两轴重合意味着两次旋转绕的是同一个轴，所以说，三个自由度变为了两个自由度。

---

数学表示

接下来我们从数学的角度来理解一下死锁为什么会发生，结合上文的形象表示，理解起来更容易。

我们在上文已经求了在 \(ZYX\) 顺规下的旋转矩阵为

\[\begin{aligned} R_{ZYX} &=R_1 R_2 R_3 \\ &=\begin{bmatrix} c\alpha c\beta & c\alpha s\beta s\gamma - c\gamma s\alpha& s\alpha s\gamma + c\alpha c\gamma s\beta \\ c\beta s\alpha & c\alpha c\gamma + s\alpha s\beta s\gamma & c\gamma s\alpha s\beta - c\alpha s\gamma \\ -s\beta & c\beta s\gamma & c\beta c\gamma \end{bmatrix} \end{aligned}\]

现在把 \(\beta=90°\) 带进去看一下旋转矩阵有什么结果，此时旋转矩阵变成了这样。

\[\begin{aligned} R_{ZYX} &=R_1 R_2 R_3 \\ &=\begin{bmatrix} 0 & -s(\alpha - \gamma)& c(\alpha-\gamma) \\ 0 & c(\alpha-\gamma) & s(\alpha-\gamma) \\ -1 & 0 & 0 \end{bmatrix} \end{aligned}\]

可以发现，此时的 \(\alpha\) 和 \(\gamma\) 其实是一个变量 \(\alpha-\gamma\)，这也从另一个角度说明了在这种情况下，少了一个自由度，所以出现了“万向节死锁”。