【Leetcode】二分系列
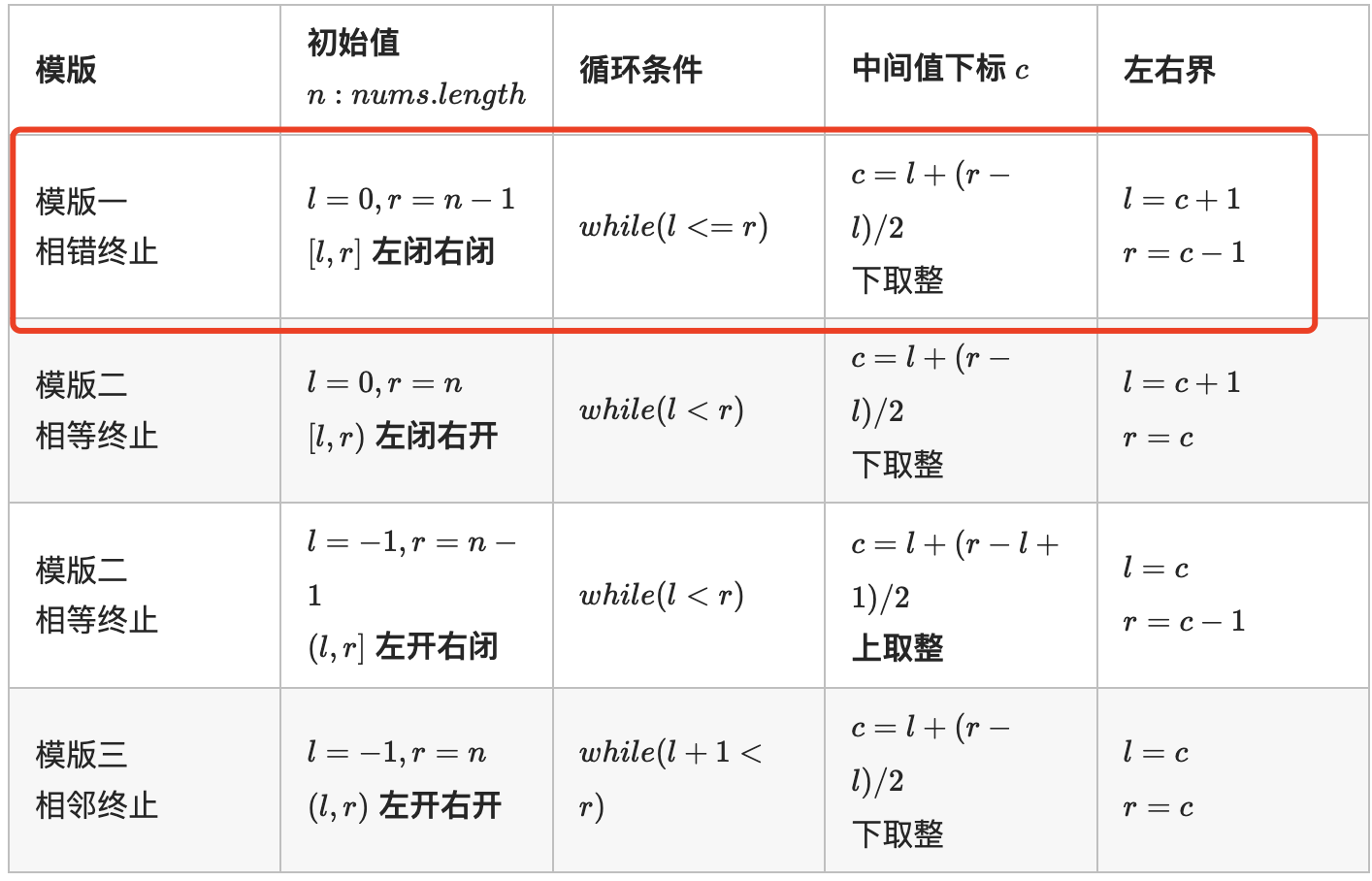
【规律总结】
1.查找采用标准二分框架
def midFind(): l, r = 0, len(nums) - 1 while l <= r: m = l + (r - l) // 2 if nums[m] == target: return mid elif nums[m] < target: # 需要往右走 l = m + 1 else: # 需要往左走 r = m - 1 return -1
2.不可能满足要求的正常往下走,满足要求的判断是否第一个/最后一个
3.初始值:l,r初始值永远不变
4.循环条件:l<=r永远不变
5.更新条件:r更新r=m-1,当m位置可以取到时更新为r=m,当有重复数字时更新为r=r-1。但l更新不可能从m+1变成m,但发现有l=l+1的情况
6.返回值:尽量在中间找到一个合适的位置返回,一般为=target或者l=r。如果找不到,则返回l
7.不完全有序数组,需要找到有序的一段进行判断走向
【Leetcode-33】
一、题目:搜索旋转排序数组
整数数组 nums 按升序排列,数组中的值 互不相同 。
在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]](下标 从 0 开始 计数)。例如, [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。
给你 旋转后 的数组 nums 和一个整数 target ,如果 nums 中存在这个目标值 target ,则返回它的索引,否则返回 -1 。
二、代码:
def search(self, nums: List[int], target: int) -> int: l, r = 0, len(nums) - 1 while l <= r: m = l + (r - l) // 2 if nums[m] == target: return m elif nums[m] >= nums[l]: # 左有序,通过左段判断是否在里面从而确定走向 if nums[l] <= target < nums[m]: # 在左段 r = m - 1 else: # 在右段 l = m + 1 else: # 右有序 if nums[m] < target <= nums[r]: # 在右段 l = m + 1 else: # 在左段 r = m - 1 return -1
三、参考资料
https://leetcode.cn/problems/search-in-rotated-sorted-array/solution/yi-wen-dai-ni-shua-bian-er-fen-cha-zhao-dtadq/
【Leetcode-34】
一、题目:在排序数组中查找元素的第一个和最后一个位置
给定一个按照升序排列的整数数组 nums,和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
二、代码:
def searchRange(self, nums: List[int], target: int) -> List[int]: """ 标准二分架构,找到时判断是否是第一个/最后一个,不是则往可能是的方向走 """ def getFisrt(): l, r = 0, len(nums) - 1 while l <= r: m = l + (r - l) // 2 if nums[m] == target: # 可能是第一个,也可能需要往左走找第一个 if m == l or nums[m - 1] < target: # 是第一个 return m else: r = m - 1 elif nums[m] > target: # 需要往左走 r = m - 1 else: l = m + 1 return -1 def getEnd(): l, r = 0, len(nums) - 1 while l <= r: m = l + (r - l) // 2 if nums[m] == target: # 可能是最后一个,也可能需要往右走再找 if m == r or nums[m + 1] > target: # 是最后一个 return m else: l = m + 1 elif nums[m] > target: # 需要往左走 r = m - 1 else: l = m + 1 return -1 s, e = getFisrt(), getEnd() return [s, e]
三、参考资料
https://leetcode.cn/problems/search-in-rotated-sorted-array/solution/yi-wen-dai-ni-shua-bian-er-fen-cha-zhao-dtadq/
【Leetcode-35】
一、题目:搜索插入位置
给定一个升序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
你可以假设数组中无重复元素。
二、代码:
def searchInsert(self, nums: List[int], target: int) -> int: """ 标准二分写法,根据测试用例得知最终返回l的位置 """ l, r = 0, len(nums) - 1 while l <= r: mid = l + (r - l) // 2 if nums[mid] == target: return mid elif nums[mid] < target: l = mid + 1 else: r = mid - 1 return l
三、参考资料
https://leetcode.cn/problems/search-in-rotated-sorted-array/solution/yi-wen-dai-ni-shua-bian-er-fen-cha-zhao-dtadq/
【其他】
一、题目:给定一个升序数组和一个目标值,在数组中找到第一个大于目标值的索引,如果不存在则返回-1
二、代码:
def getFisrt(): l, r = 0, len(nums) - 1 while l <= r: m = l + (r - l) // 2
if nums[m] <= target: # 需要往右走 l = m + 1 else: if m == l or nums[m-1] <= target: return m else: r = m - 1 return -1 nums = [1, 3, 5, 5, 6] target = 7 # 0, 1, 2, 5, 7 print(getFisrt())
三、参考资料
https://leetcode.cn/problems/search-in-rotated-sorted-array/solution/yi-wen-dai-ni-shua-bian-er-fen-cha-zhao-dtadq/
【其他】
一、题目:给定一个升序数组和一个目标值,在数组中找到最后一个小于目标值的索引,如果不存在则返回-1
二、代码:
def getFisrt(): l, r = 0, len(nums) - 1 while l <= r: m = l + (r - l) // 2 if nums[m] >= target: # 需要往左走 r = m - 1 else: if m == r or nums[m+1] >= target: return m else: l = m + 1 return -1 nums = [1, 3, 5, 5, 6] target = 0 # 0, 1, 2, 5, 7 print(getFisrt())
三、参考资料
https://leetcode.cn/problems/search-in-rotated-sorted-array/solution/yi-wen-dai-ni-shua-bian-er-fen-cha-zhao-dtadq/
【Leetcode-69】
一、题目:x的平方根
实现 int sqrt(int x) 函数。
计算并返回 x 的平方根,其中 x 是非负整数。
由于返回类型是整数,结果只保留整数的部分,小数部分将被舍去。
二、代码:
def mySqrt(self, x: int) -> int: """ 二分,找一个平方<=x的数,最后走到的点是最接近的点 """ l, r = 0, x res = 0 while l <= r: m = l + (r - l) // 2 val = m * m if val <= x: l = m + 1 res = m else: r = m - 1 return res
【Leetcode-74】
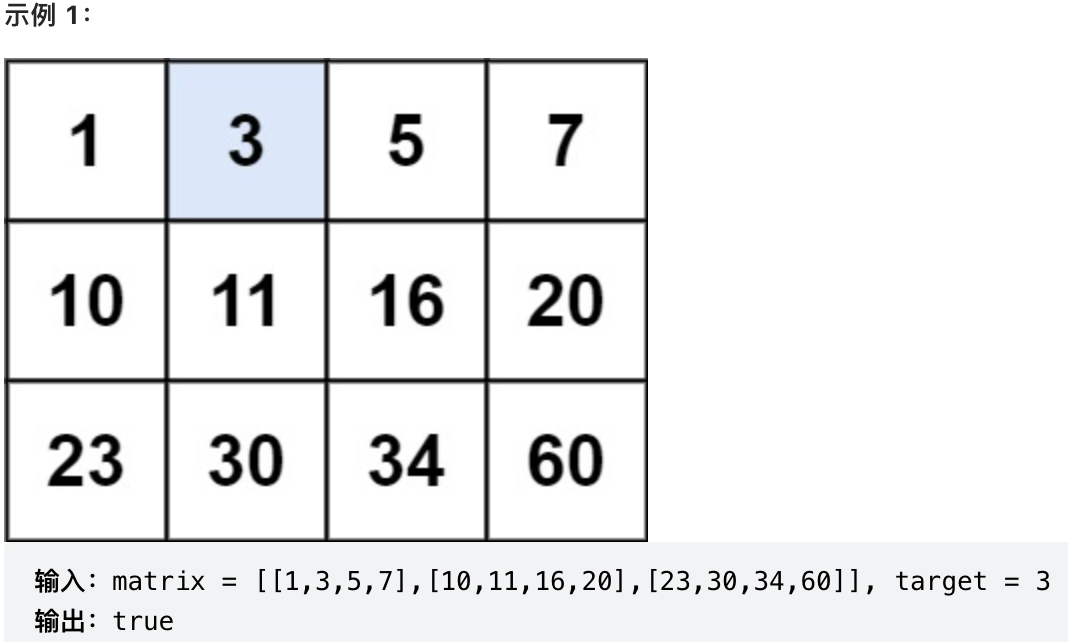
一、题目:搜索二维矩阵
编写一个高效的算法来判断 m x n 矩阵中,是否存在一个目标值。该矩阵具有如下特性:
每行中的整数从左到右按升序排列。
每行的第一个整数大于前一行的最后一个整数。
二、代码:
def searchMatrix(self, matrix: List[List[int]], target: int) -> bool: """ 二分 """ i, j = len(matrix) - 1, 0 while i >= 0 and j < len(matrix[0]): # 不超出边界 if matrix[i][j] == target: return True elif matrix[i][j] > target: # 往上走 i -= 1 else: # 往右走 j += 1 return False
【Leetcode-81】
一、题目:搜索旋转排序数组2
已知存在一个按非降序排列的整数数组 nums ,数组中的值不必互不相同。
在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了 旋转 ,使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]](下标 从 0 开始 计数)。例如, [0,1,2,4,4,4,5,6,6,7] 在下标 5 处经旋转后可能变为 [4,5,6,6,7,0,1,2,4,4] 。
给你 旋转后 的数组 nums 和一个整数 target ,请你编写一个函数来判断给定的目标值是否存在于数组中。如果 nums 中存在这个目标值 target ,则返回 true ,否则返回 false 。
二、代码:
def search(self, nums: List[int], target: int) -> int: l, r = 0, len(nums) - 1 while l <= r: m = l + (r - l) // 2 if nums[m] == target: return True elif nums[m] >= nums[l]: # 左不一定有序,通过左段判断是否在里面从而确定走向 if nums[l] <= target < nums[m]: # 一定在左段 r = m - 1 else: # 可能在右段也可能在左段如[1,0,1,1,1] l = l + 1 # l = m + 1 else: # 右不一定有序 if nums[m] < target <= nums[r]: # 一定在右段 l = m + 1 else: # 可能在左段也可能在右段 r = r - 1 # r = m - 1 return False
三、参考资料
https://leetcode.cn/problems/search-in-rotated-sorted-array/solution/yi-wen-dai-ni-shua-bian-er-fen-cha-zhao-dtadq/
【Leetcode-153】
一、题目:寻找旋转排序数组中的最小值
已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到:
若旋转 4 次,则可以得到 [4,5,6,7,0,1,2]
若旋转 7 次,则可以得到 [0,1,2,4,5,6,7]
注意,数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。
给你一个元素值 互不相同 的数组 nums ,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。
你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
示例:输入nums = [3,4,5,1,2],输出1;输入nums = [4,5,6,7,0,1,2],输出0;输入nums = [11,13,15,17]输出11.
二、代码:
def findMin(self, nums: List[int]) -> int: """ 首先找到出口,出口是序列递增&第一个是最小值 其次根据示例找到规律为:左有序则最小值在右边,右有序则最小值在左边 """ l, r = 0, len(nums) - 1 while l <= r: m = l + (r - l) // 2 if nums[l] <= nums[r]: # 序列递增,说明最左边就是最小的 return nums[l] elif nums[m] >= nums[l]: # 说明左有序,最小值在右边,且不包含m位置 l = m + 1 else: # 说明右有序,最小值在左边,且可能取到m r = m return -1
三、参考资料
https://leetcode.cn/problems/search-in-rotated-sorted-array/solution/yi-wen-dai-ni-shua-bian-er-fen-cha-zhao-dtadq/
【Leetcode-154】
一、题目:旋转数组的最小数字
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。输入一个递增排序的数组的一个旋转,输出旋转数组的最小元素。例如,数组 [3,4,5,1,2] 为 [1,2,3,4,5] 的一个旋转,该数组的最小值为1。
注意:包含重复数字
二、代码:
def minArray(self, nums: List[int]) -> int: """ 根据测试用例总结规律 [1], [1, 3, 3], [3, 1, 3], [2, 2, 2, 0, 2], [3, 4, 5, 1, 2] """ if len(nums) == 1: return nums[0] l, r = 0, len(nums) - 1 while l <= r: m = l + (r - l) // 2 if nums[m] == nums[r]: r = r - 1 elif nums[m] > nums[r]: # 左升序,最小在右 l = m + 1 else: # 右升序,最小在左 r = m return nums[l]
【Leetcode-162】
一、题目:寻找峰值
峰值元素是指其值大于左右相邻值的元素。
给你一个输入数组 nums,找到峰值元素并返回其索引。数组可能包含多个峰值,在这种情况下,返回 任何一个峰值 所在位置即可。
二、代码:
def findPeakElement(self, nums: List[int]) -> int: """ 左边数小,右边一定至少有一个峰值(左边不确定有没有,但右边一定有) """ l, r = 0, len(nums) - 1 while l <= r: m = l + (r - l) // 2 if m == 0 or nums[m] > nums[m-1]: # 右边一定有 if m == len(nums) - 1 or nums[m+1] < nums[m]: return m else: l = m + 1 else: # 左边一定有 r = m - 1
【Leetcode-287】
一、题目:寻找重复数
给定一个包含 n + 1 个整数的数组 nums ,其数字都在 1 到 n 之间(包括 1 和 n),可知至少存在一个重复的整数。
假设 nums 只有 一个重复的整数 ,找出 这个重复的数 。
二、代码:
def findDuplicate(self, nums: List[int]) -> int: """ 在1-n随机猜一个数m,统计<=m的数量cnt cnt>m说明重复数在1-m且m可以取到 cnt<=m说明重复数在m+m+1-n 当只有1个数时说明该数就是重复数 m取中间值每次可以砍掉一半,因此是二分法 """ l, r = 1, len(nums) while l <= r: m = l + (r - l) // 2 cnt = 0 for num in nums: if num <= m: cnt += 1 if l == r: return m elif cnt > m: r = m else: l = m + 1
【Leetcode-378】
一、题目:有序矩阵中第K小的元素
给你一个 n x n 矩阵 matrix ,其中每行和每列元素均按升序排序,找到矩阵中第 k 小的元素。
请注意,它是 排序后 的第 k 小元素,而不是第 k 个 不同 的元素。
二、代码:
def kthSmallest(self, matrix: List[List[int]], k: int) -> int: """ 值域二分 首先猜测一个可能的数(中间数)m,计算<=m的数量,m最多(右重复数字)为第p大 p<k,则一定只能往大了走,此时l=m+1 p>k,只能往小了走,但可能取到m,有重复值的情况下能取到 p=k,不能直接返回,因为m可能不存在matrix中!只能在更小的数找 """ def get_cnt(target): i, j = len(matrix) - 1, 0 num = 0 while i >= 0 and j < len(matrix[0]): if matrix[i][j] <= target: num += i + 1 j += 1 else: i -= 1 return num l, r = matrix[0][0], matrix[-1][-1] while l <= r: m = l + (r - l) // 2 # 猜的数 p = get_cnt(m) # 计算<=m的数量, m(最多,有重复数字的情况下)为第p大 if l == r: return m if p >= k: # 往小了找,当前m可能 r = m else: # 往大找,m不可能,因为可能重复数字 l = m + 1


