2024省选联测14

A. 整除

求有多少个正整数 \(x\) 满足 \(c_0x^{a_0}+c_1x^{a_1}+...+c_{n-1}x^{a_{n-1}}\) 能被 \(x^0+x^1+...+x^{m-1}\) 整除，\(|c_i|=1\)。

特判 \(x=1\) 是否可行。

\[\begin{aligned} S&=x^0+x^1+...+x^{m-1}\\ \\ xS&=x^1+...+x^{m-1}+x^m\\ \\ S&=\dfrac{x^m-1}{x-1} \end{aligned} \]

设 \(f(x)=c_0x^{a_0}+c_1x^{a_1}+...+c_{n-1}x^{a_{n-1}}\)。

即求有多少 \(x\) 满足 \(f(x)\cdot(x-1)\bmod(x^m-1)=0\)。
\({}\)
设 \(f(x)\cdot(x-1)\bmod(x^m-1)=\sum_{i=0}^{m-1}b_ix^i\)。

当 \(b_i=0\) 或 \(x-1\) 或 \(-x+1\) 时满足条件。

先求出 \(b_i\)，若 \(b_i=0\) 则有无数解。

否则，枚举 \(x\)，不断进行以下操作：

• 若 \(b_i\ge x\)，则将 \(b_i\) 减去 \(x\)，\(b_{(i+1)\bmod m}\) 加上 \(1\)。
• 若 \(b_i\le-x\)，则将 \(b_i\) 加上 \(x\)，\(b_{(i+1)\bmod m}\) 减去 \(1\)。

判断得到的 \(b_i\) 是否满足条件。

每次操作会使 \(b_i\) 的绝对值之和至少减少 \(x-1\)，总操作数为 \(O(n\log n)\)。使用 map 维护，时间复杂度 \(O(n\log^2 n)\)。

点击查看代码

bool cmp(pair <int, int> x, pair <int, int> y) {return abs(x.first) > abs(y.first);}

int get(int x)
{
    int res = k, ans = s; cnt = 0;
    for(int i = 1; i <= tot && abs(c[i].first) >= x; ++ i)
        q.push(c[i].second);

    while(!q.empty())
    {
        int u = q.front(); q.pop(); t[++cnt] = u;
        if(abs(b[u]) < x) continue;

        res -= b[u] - b[u] % x;
        res -= b[(u + 1) % m];
        ans -= abs(b[u]) + abs(b[(u + 1) % m]);
        b[(u + 1) % m] += b[u] / x; b[u] %= x;
        ans += abs(b[u]) + abs(b[(u + 1) % m]);
        res += b[(u + 1) % m];
        q.push((u + 1) % m);
    }

    for(int i = 1; i <= cnt; ++ i) b[t[i]] = a[t[i]];

    return ans == 0 || abs(res) == m * (x - 1);
}

void work()
{
    int sum = 0, ans = 0, o = 1; a.clear(); tot = 0;

    scanf("%lld%lld", &n, &m);
    for(int i = 1, x, y; i <= n; ++ i)
        scanf("%lld%lld", &y, &x), a[(x + 1) % m] += y, a[x % m] -= y, sum += y;

    for(auto i : a) o &= i.second == 0;

    if(o) {printf("-1\n"); return;}

    ans = sum % m == 0; b = a; k = 0; s = 0;
    for(auto i : a)
    {
        if(!i.second) continue;
        c[++tot] = {i.second, i.first};
        k += i.second; s += abs(i.second);
    }

    sort(c + 1, c + 1 + tot, cmp);
    for(int i = 2; i <= abs(c[1].first) + 1; ++ i) ans += get(i);

    printf("%lld\n", ans);
}

B. 词典

一个 01 串 \(s\) 是单词当且仅当 \(s\) 中不包含两个连续的 \(0\)。

一个包含 \(n\) 个单词的词典是 \(n\) 个单词的集合，且满足其中任意一个单词都不是任意其他单词的前缀。

给定一个词典 \(D\)，定义 01 串 \(s\) 的代价 \(C(S)=\sum_{j=1}^k\lfloor(1+\log_2j)\rfloor\)，其中 \(k\) 是 \(D\) 中满足 \(s\) 是 \(t\) 的前缀的单词数量。该词典 \(D\) 的代价即为所有 01 串的代价之和。

例如，考虑一个包含 \(4\) 个单词的词典 \(\{0,10,110,111\}\)。这个词典的代价为

\[C(\epsilon)+C(0)+C(1)+C(10)+C(11)+C(110)+C(111)=8+1+5+1+3+1+1=20 \]

这里 \(\epsilon\) 表示空串。求包含 \(n\) 个单词的词典的代价的最小值。

设答案为 \(f(n)\)，\(g(n)=\sum_{i=1}^n\lfloor1+\log_2j\rfloor\)。

钦定左儿子为 \(0\)，右儿子为 \(1\)。Trie 树上每个叶子结点是一个单词，每个结点作为一个前缀求代价。

\[f(n)=g(n)+\min_{1\le k\le n-1}\{[k>1]g(k)+f(k)+f(n-k)\} \]

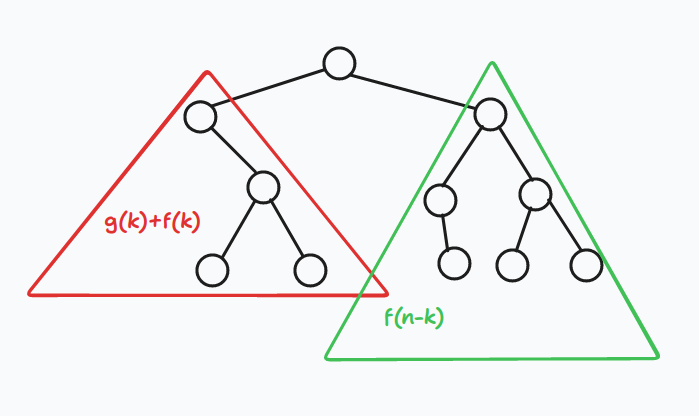
发现 \(g(n)\) 是 \(O(n\log n)\) 级别，\(f(n)\) 是 \(O(n\log^2n)\) 级别，\(f(n)-f(n-1)\) 是 \(O(\log^2n)\) 级别。对于每个 \(v\) 求出最大的 \(m\) 满足 \(f(m)-f(m-1)=v\)，查询时二份答案。

对于每个 \(v\) 变化的点，我们二分求出下一个转折点。在二分过程中，我们需要求得 \(f(n)\) 值。三分求出 \(\min_{1\le k\le n-1}\{[k>1]g(k)+f(k)+f(n-k)\}\) 在哪里取最小值。\(g(n)\) 可以直接 \(O(\log n)\) 求出。

点击查看代码

struct Node
{
    int pos, delta, val;
    friend bool operator < (Node x, Node y)
        {return x.pos == y.pos ? (x.delta == y.delta ? x.val < y.val : x.delta < y.delta) : x.pos < y.pos;}
} s[N];

int G(int x)
{
    if(x <= n) return g[x]; int res = 0, j = __lg(x);
    for(int i = 1; i <= j; ++ i) res += i * (1ll << i - 1);
    return res + (j + 1) * (x - (1ll << j) + 1);
}

// 根据已知断点求 f
int F(int x)
{
    if(x <= n) return f[x];
    int p = lower_bound(s + 1, s + 1 + top, (Node){x, 0, 0}) - s;
    return s[p - 1].val + s[p].delta * (x - s[p - 1].pos);
}

int P(int i, int j) {return (j > 1) * G(j) + F(j) + F(i - j);}

int D(int x)
{
    int l = x * 0.33, r = x * 0.66, ans = 3e18;
    while(r - l > 30)
    {
        int mid1 = l + (r - l) / 3.0, mid2 = r - (r - l) / 3.0;
        P(x, mid1) > P(x, mid2) ? l = mid1 : r = mid2;
    }
    for(int i = l; i <= r; ++ i) ans = min(ans, P(x, i));
    return ans + G(x);
}

void work()
{
    for(int i = 1; i <= n; ++ i) g[i] = g[i - 1] + __lg(i) + 1; f[1] = 1;
    for(int i = 2, j = 1; i <= n; ++ i)
    {
        while(j < i && P(i, j) > P(i, j + 1)) ++ j;
        f[i] = g[i] + P(i, j);

        if(f[i] - f[i - 1] != f[i - 1] - f[i - 2])
            s[++top] = {i - 1, f[i - 1] - f[i - 2], f[i - 1]}; 
    }
    while(s[top].pos < 1e15)
    {
        int diff = D(s[top].pos + 1) - s[top].val;
        int l = s[top].pos + 1, r = l * 1.03, ans;

        while(l <= r)
        {
            int mid = l + r >> 1;
            D(mid) - D(mid - 1) == diff ? l = mid + 1, ans = mid : r = mid - 1;
        }
        s[top + 1] = {ans, diff, s[top].val + diff * (ans - s[top].pos)}; ++ top;
    }
}

signed main()
{
    freopen("dictionary.in", "r", stdin);
    freopen("dictionary.out", "w", stdout);

    work();

    int x; scanf("%lld", &T);
    while(T --) scanf("%lld", &x), printf("%lld\n", F(x));

    return 0;
}