11月份test总结
test-53
A:选举
【题目描述】
Alice和Bob要竞选魔方市市长。
有n个选民,编号为1~n,它们中有的人支持Alice,有的人支持Bob,还有的人保持中立。
现在你需要把选民分成若干个区间,每个区间的长度在[l,r]中。如果一个区间中支持Alice的人比支持Bob的人多,那么Alice得一票,一个区间中支持Bob的人比支持Alice的人多,那么Bob得一票。
Alice想要赢得选举,于是它请你合理地分区间,使得它获得的票数减去Bob获得的票数最大。
神似某次考试题(但难度不一样)
【Ans】
设 f(s)f(s) 表示 0101 串 ss 中所有 11 的位置的下标的和。那么操作 A 和操作 B 分别需要满足:
f(si)+kx≡f(si+1)(modn)f(si)+1≡f(si+1)(modn)
可得:
kx≡1(modn)
kx≡1(modn)
所以当 kk 与 nn 不互质时,无解。
B:卡片
【题目描述】
小象有n张卡片,第i张卡片上有一个数字ai。Alice和Bob轮流选择卡片 (不能重复),如果某次选择后已选择的卡片上的数字的最大公约数为1或者没有卡片可以选择,那么当前角色失败。
你需要求出:1、如果双方都选择最优策略,谁会获胜;2、如果双方都随机选取,Alice获胜的概率。
【Ans】
首先把所有的可以互相到达的点用并茶几缩一下。
对于传送门的情况可以 Floyd 跑一遍也可以 bitset 整一遍,还可以对于一个询问直接搜一下
跑步
【题目描述】
小C同学认为跑步非常有趣,于是决定制作一款叫做《天天爱跑步》的游戏。《天天爱跑步》需要玩家完成打卡任务。
这个游戏的地图可以看做一棵包含n个结点和n−1条边的树,每条边连接两个结点,且任意两个结点存在一条路径互相到达。树上结点的编号为从1到n的连续正整数。新的一天开始时,某个玩家在第0秒从自己的起点出发,以每秒跑一条边的速度,不间断地沿着最短路径向着自己的终点跑去,跑到终点后该玩家就算完成了打卡任务。(由于地图是一棵树,所以每个人的路径是唯一的)
小C想知道游戏的活跃度,所以在每个结点上都放置了一个观察员。在结点j的观察员会选择在第Wj秒观察玩家,一个玩家能被这个观察员观察到当且仅当该玩家在第Wj秒也正好到达了结点j。小C想知道每个观察员会观察到多少人?
注意:我们认为一个玩家到达自己的终点后该玩家就会结束游戏,他不能等待一段时间后再被观察员观察到。即对于把结点j作为终点的玩家:若他在Wj秒之前到达终点,则在结点j的观察员不能观察到该玩家;若他正好在第Wj秒到达终点,则在结点j的观察员可以观察到这个玩家。
但是这个游戏实在是太难了,所以游戏还增加了充钱的功能,玩家可以在报刊亭购买《骏网一卡通》(有10、30、50、100面额,据说从某时候开始还会收税)来获得加成(其实有时候米米卡、多多卡之类的便宜一些)。具体来说,某人充了一张卡后,可以对地图上的边进行修改,删除边(a,b),并添加边(c,d),同时,为了维持服务器正常运行,保证地图仍然是一棵树。随着树形态的变化,小C为了更全面地了解活跃度,决定在某些时刻修改某个Wj。
【Ans】
emmm……改编题,
前NOIP原题
test-54
A:
【题目描述】
【Ans】
我们把一个物品看做 Ai 与 Bi
之间的连边。
那么如果加入这条边之后联通块中有超过两个环或者两个环就是不合法的,也就是合法的状态只能是一个基环树和树的森林这样一个形态。
直接并茶几判断连通性,标记一下当前的联通块中是否有环就好了。
B:
【题目描述】
【Ans】
只学会了一个状压的做法。。。
首先有一个定理:
棵无根生成树,经典问题prufer序列证明
扩展Cayley定理:被确定边分为大小为a1,a2,⋯,am
的连通块,则有nm−2∏ai
test-55
A:军训
【Ans】
解题思路
不算特别难的题,但是有一点细节。。。
首先需要并茶几缩一下点,然后判断一下是否合法,由于我们需要字典序最小的,因此我们应当保证一个联通块中标号较小的点为根节点。
那么对于所有不能够相等的标号对,我们再标号较大的点记下来标号较小的点的限制,然后从前往后扫一遍取 mex
值就好了。
B:命题规范
【Ans】
确实是一个李超线段树的好题。。。
发现一个位置 p 的最后答案其实就是对于以 p 为右端点向左边拓展,以 p+1 为左端点可以向右边拓展的最优解。
这两种情况类似只讨论第一种情况,记前缀和数组是 prea,preb
那么最优解就是 max1≤l≤r{(prear−preal−1)−k(prebr−prebl−1)}
对于一个右端点 p 而言答案就是 preap−k×prebp+max0≤i<p{prebi×k−preai}
直接以 k 为下标,李超线段树维护就好了。
C:前置知识
【Ans】
解题思路
只学会了一个状压的做法。。。
首先有一个定理:
棵无根生成树,经典问题prufer序列证明
扩展Cayley定理:被确定边分为大小为a1,a2,⋯,am
的连通块,则有nm−2∏ai
然后我们枚举那些边是连接的然后根据上面的定理求出来一个至少有若干条边相同的值,然后二项式反演就好了。
test-56
A:环
【题目描述】
给定一个长度为 n 的 0101 串,定义两种类型的操作:
操作 A:选择一个 x,将序列循环右移 x 位。
操作 B:选择一个 x,满足序列的第 x 个位置为 1,且第 (x+1)modn 的位置不为 1,交换序列的第 x 个位置和第 (x+1) mod n 个位置的字符。
给定 n, k, ln, k, l,构造一个由 l 个长度为 n 的 0101 串构成的序列 S,序列中的每个串恰好有 k 个 11。且对于任意一个串 si,都既可以通过操作 A,也可以通过操作 B 变为 si+1。
【Ans】
设 f(s)f(s) 表示 0101 串 ss 中所有 11 的位置的下标的和。那么操作 A 和操作 B 分别需要满足:
f(si)+kx≡f(si+1)(modn)f(si)+1≡f(si+1)(modn)
可得:
kx≡1(modn)
kx≡1(modn)
所以当 kk 与 nn 不互质时,无解。
#include <stdio.h>
#include <stdlib.h>
#include <algorithm>
#include <string.h>
#include <math.h>
#define lld long long
using namespace std;
const int N = 110;
int T, n, k, l;
inline int exgcd(int a, int b, int &p, int &q){
if (!b) return p = 1, q = 0, a;
int ret = exgcd(b, a % b, q, p);
q -= a / b * p;
return ret;
}
inline int inv(int a, int b) {
int p, q;
exgcd(a, b, p, q);
return (p % b + b) % b;
}
int a[N];
int main() {
scanf("%d", &T);
for (; T --; ) {
scanf("%d%d%d", &n, &k, &l);
if (__gcd(n, k) != 1) {
puts("NO");
continue;
}
puts("YES");
int ik = inv(k, n);
for (int i = 1; i <= l; ++ i) {
memset(a, 0, sizeof(a));
for (int j = 0; j < k; ++ j)
a[(i + j) % n * ik % n] = 1;
for (int j = 0; j < n; ++ j)
putchar('0' + a[j]);
puts("");
}
}
}
B:DNA 序列
【题目描述】
给定 nn 个只包含 A, C, G, TA, C, G, T 的字符串,对于每一个字符串,取出它的一个前缀,最后以任意顺序首尾拼接起来,求能得到的最小的字符串。
【Ans】
假如确定了顺序,那么最后一个串一定只会选取其第一个字符。确定顺序之后进行贪心即可。
C:探寻
【题目描述】
给出一个带边权的有根树,根为 11,每个节点都有一个权值,每次经过一条之前未经过的边时,需要花费边权的代价,每次经过一个之前未经过的点,可以获得点权大小的钱。当钱数目为 00 时结束游戏。求初始钱数最小为多少时,可以走到叶子节点。
【Ans】
把每个节点向其父亲节点连边的边权作为到达节点的代价。那么要想让初始钱数最少,一定走完了所有可以收益的节点。对于每个节点维护一个 setset,存储子树内所有节点的代价,将代价从小到达排序,贪心地选取即可。
test-57
A:精神焕发
【题目描述】
给出一棵 n 个点的树,点从 1 至 n 编号。每个点 u 上有足够多瓶加血 wu 的药水,如果原来你的血量为 x,那么喝下这瓶药水后你的血量会变为 x+wu。
有 q 次询问。每次询问给出数 x 与两个点的编号 s、t。
这次询问中,你的初始血量为 x,一开始在 s,想要走到 t。每次走到一个点,你就会喝下这个点上的药水(一开始来到点 s 时会喝下 s 上的药水)。你可以多次经过一个点,每次经过时都会喝下一瓶这个点上的药水。如果某个时刻你的血量小于 0,那么你就死了。你想知道你是否可以在不死的情况下从 s 走到 t。
更形式化地,你需要判断是否存在一个点的编号组成的序列 p1…k,满足:
p1=s,pk=t;
对于任意 i∈[1,k−1],树上的点 pi 与 pi+1 之间有一条边。
对于任意 i∈[1,k],有 x+∑j=1iwpj≥0。
pp 的长度 kk 可以由你决定,并且 pp 中可以存在相同的元素。
【Ans】
从 s 到 t 如果不走最短的路径,而是绕到一些地方加血,那么必然经过一条两端点权值和 >0 的边。
如果到达了这样的边的任意一个端点,那么可以获得无限血,我们把这样的点标记为无限血点。
所以要么从 s 走最短路径到 t,要么从 s 走最短路径到无限血点,获得无限血后再走到 t
第二种情况可以通过 up and down DP 维护从每个点最少需要多少血才能到达一个无限血点。
第一种情况即求 s 到 t 路径上的前缀最小值,容易发现前缀最小值是整个路径或是整个路径除去 t 点,否则路径上一定有无限血,可以第二种情况处理
B:顺逆序对
【题目描述】
对于一个 1,…,n的排列 a1,…,an,定义 i 处的顺序对数 f(i) 为满足 1≤j<i 且 aj<ai的 j 的数量,定义 i 处的逆序对数 g(i) 为满足 i<j≤n 且 aj<ai 的 j 的数量。
给定 n,对于每个 k=0,1,…,n−1,求出满足 maxi=1n∣f(i)−g(i)∣=k的 a1,…,an的数量模 1e9+7 的值。
【Ans】
一个有意思的数学题
int n;
int main()
{
n=read();ll las=0,ans=0,fac=1;
for(ll k=0;k<n;++k,fac=fac*k%MOD){
ll hlf=(n-k)/2;
ans=fac*fpr(k+1,hlf+((n-k)&1))%MOD*fpr(k,hlf)%MOD;
printf("%lld ",(ans-las+MOD)%MOD);las=ans;
}
return 0;
}
C: 串串
【题目描述】
FAT想要烫串串。
现在有一个长度为 n 的字符串 S 与一个长度为 m 的字符串 T
定义字符串 Si 表示将从 S 的第 i 个字符后断开得到 A,B,将 B 从尾到头形成的字符串设为 B′,将 B′ 接在 A 后面得到的字符串。
对于每个 i,FAT 想知道 T 在 Si 中出现的次数。
【Ans】
T 在 Si=AB′ 中的出现次数是 T 在 A 中的出现次数 + T 在 B′ 中的出现次数 + T 跨过 A 和 B′ 的出现次数
前两个很好处理,考虑最后一个
T 的一个后缀要与 B′ 的前缀匹配,剩余的前缀要与 A 的后缀匹配
可以先处理出所有跟 B′ 的前缀匹配的 T 后缀,然后询问它们剩的前缀有多少个是 A 的后缀
可以建出 KMP 的 fail tree 解决
时间复杂度 O(nlogn)
test-58
A:GCD和LCM
【题目描述】
现在有T个询问,每个询问给你三个整数n,m,a,求对于所有1<=i<=n,1<=j<=m,1<=gcd(i,j)<=a 的i,j,对1e9取模。
【Ans】
莫比乌斯反演+树状数组BIT
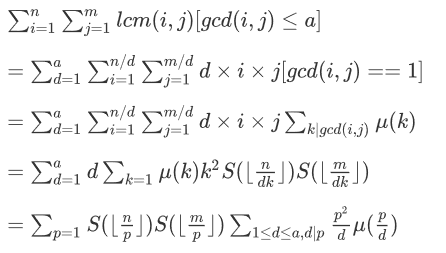
对于后面的,考虑添加一个a对于答案的贡献,对于前面的,则可以直接用数论分块解决。
献上莫比乌斯反演的例题:
P1829 【国家集训队】Crash的数字表格/JZPTAB
分块模板题
类似题:数表
B:平面图
【题目描述】
【Ans】
现在已经知道有哪些边是关键边了,需要动态维护所在连通块。
隔断一条关键边的时候考虑启发式分裂,给分裂出来的较小的连通块重新标号。
讲解的时候,提到了乱搞算法:双向bfs,很不幸的是数据加强了。
11.11
\(\small双十一\)
\(\cal T1:\)序列(chain)
【题目简述】
有 \(n\) 个合数,均可以表示为\(a=p*q\) \((p,q\in prime).\)
【Ans】
正解考察的是DAG图上DP,但是 “枚举+最短路” 乱搞做法也能A,想法简单易懂,引人深思
Code
#include<bits/stdc++.h>
using namespace std;
#define INF (0x7f7f7f7f)
const int N=5e4+100;
const int M=1e6+100;
const int V=8e4+100;
map<int,int>mp;
int pd[V];
struct EDGE{
int to,nxt;
}edge[N];
struct sss{
int l,r;
}a[N];
int tot;
int rudu[V];
int head[V];
void add(int u,int v)
{
edge[++tot].to=v;
edge[tot].nxt=head[u];
head[u]=tot;
rudu[v]++;
}
int tp;
int flg[M];
int prime[M];
void init()
{
for(int i=2;i<M;i++)
{
if(!flg[i])
{
prime[++tp]=i;
mp[i]=tp;
}
for(int j=1;j<=tp&&prime[j]*i<M;j++)
{
flg[i*prime[j]]=prime[j];
if(i%prime[j]==0)break;
}
}
}
int dis[V];
int vis[V];
int SPFA(int s)
{
int ans=-INF;
for(int i=1;i<V;i++)
{
dis[i]=-INF;
}
memset(vis,0,sizeof vis);
dis[s]=0;
queue<int>q;
q.push(s);
vis[s]=1;
while(!q.empty())
{
int u=q.front();
q.pop();
for(int i=head[u];i;i=edge[i].nxt)
{
int v=edge[i].to;
if(dis[v]<dis[u]+1)
{
dis[v]=dis[u]+1;
if(!vis[v])
{
q.push(v);
}
}
}
}
for(int i=1;i<V;i++)
{
ans=max(ans,dis[i]);
}
return ans;
}
int main()
{
init();
int n;
scanf("%d",&n);
int x;
for(int i=1;i<=n;i++)
{
scanf("%d",&x);
a[i].l=flg[x];
a[i].r=x/flg[x];
add(mp[a[i].l],mp[a[i].r]);
}
int tmp=0;
for(int i=1;i<=n;i++)
{
if(rudu[mp[a[i].l]]==0&&pd[mp[a[i].l]]==0)
{
pd[mp[a[i].l]]=1;
tmp=max(tmp,SPFA(mp[a[i].l]));
}
}
printf("%d",tmp);
return 0;
}
\(\cal T2:\)生成最小树(mintree)
【题目简述】
给一张(n,m)的图,从中选出一棵生成树,每次可以选择树上一条边使其边权-1,为至少需要多少次操作会使它变为最小生成树?(保证联通且无重)
【Ans】
需要用到严格次小生成树,

Code
typedef long long ll;
const int MAXN=10010, MAXM=200010;
int vis[MAXN],pos=0;
map<pair<int,int>,int> MP;
vector<int> notTree;
ll ans=0;
struct edge{
int from,to,weight;
bool inTree;
}Edges[MAXM];
struct node{
int parent,weight,height;
vector<int> childs;
void set(int w)
{
if(weight>w)
{
ans+=weight-w;
weight=w;
}
}
}Nodes[MAXN];
void add(int a,int b,int weight)
{
Edges[pos].weight=weight;MP[make_pair(a,b)]=pos;
Edges[pos].from=a;Edges[pos].to=b;
Nodes[a].childs.push_back(pos);pos++;
Edges[pos].weight=weight;MP[make_pair(b,a)]=pos;
Edges[pos].from=b;Edges[pos].to=a;
Nodes[b].childs.push_back(pos);pos++;
}
bool cmp(int a, int b)
{
return Edges[a].weight<Edges[b].weight;
}
void DFS(int x, int height)
{
if(vis[x])return;
vis[x]=true;
for(int i=0;i<Nodes[x].childs.size();i++)
{
int eid = Nodes[x].childs[i];
int to = Edges[eid].to;
if(Edges[eid].inTree)
{
if(vis[to]) continue;
Nodes[to].weight = Edges[eid].weight;
Nodes[to].height = height + 1;
Nodes[to].parent = x;
DFS(to, height + 1);
}
else if(to < x)
notTree.push_back(eid);
}
}
int un(int a, int b, int w)
{
if(a == b) return a;
node na = Nodes[a], nb = Nodes[b];
int p;
if(na.height == nb.height)
{
Nodes[a].set(w);
Nodes[b].set(w);
p = un(na.parent, nb.parent, w);
}
else if(na.height > nb.height)
{
Nodes[a].set(w);
p = un(na.parent, b, w);
}
else
{
Nodes[b].set(w);
p = un(a, nb.parent, w);
}
if(a != p)
Nodes[a].parent = p;
if(b != p)
Nodes[b].parent = p;
return p;
}
int main()
{
int n, m, u, v, weight;
cin >> n >> m;
for (int i = 1; i <= m; i++)
{
cin >> u >> v >> weight;
add(u, v, weight);
}
for (int i = 1; i < n; i++)
{
cin >> u >> v;
Edges[MP[make_pair(u, v)]].inTree = true;
Edges[MP[make_pair(v, u)]].inTree = true;
}
DFS(1, 0);
sort(notTree.begin(), notTree.end(), cmp);
for(int i = 0; i < notTree.size(); i++)
{
edge e = Edges[notTree[i]];
un(e.from, e.to, e.weight);
}
cout << ans << endl;
return 0;
}
\(\cal T3:\)互质序列(rlprime)
【题目简述】
求满足下列条件的序列的个数:
- 序列递增
- 所有数字\(\in [A,B]\) \((B-A \leqslant 100)\)
- 序列中的所有数字两两互质
【Ans】
根据老套路来讲,这题是DP,由于性质3,所以我们可以考虑枚举100以内的质数,再进行一个状压的DP来统计序列个数
Code
#define ll long long
ll A,B;
int cnt[25];
ll f[1<<23];
int prime[25]={
2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97
};
int main()
{
scanf("%lld%lld",&A,&B);
f[0]=1;
vector<int>p;
for(ll i=A;i<=B;i++)
{
for(int j=0;j<25;j++)
{
if(i%prime[j]==0)
cnt[j]++;
}
}
for(int i=0;i<25;i++)
{
if(cnt[i]>1)
p.push_back(prime[i]);
}
for(ll i=A;i<=B;i++)
{
int s=0;
for(int j=0;j<p.size();j++)
{
if(i%p[j]==0)
{
s|=(1<<j);
}
}
int S=((1<<p.size())-1)^s;
for(int j=S;j;j=(j-1)&S)
{
f[j|s]+=f[j];
}
f[s]+=f[0];
}
ll ans=0;
for(int i=0;i<(1<<p.size());i++)
{
ans+=f[i];
}
printf("%lld",ans-1);
return 0;
}
\(\cal T4:\)鬼鬼的序列(seq)
【题目简述】
给了一个由\(n\)个数组成的数列\(a\),找到最长的子串满足在其中添加小于等于\(k\)个数后变为公差为\(d\)的等差数列
【Ans】
具备上述条件的子串需要满足子串中所有的数 \(\% d\)同余,同时\(\frac{(Max-Min)}{d}-(r-l+1)\leqslant k\) 维护极差
Code
#include <algorithm>
#include <bits/stdc++.h>
#define pir pair<int, int>
using namespace std;
const int SIZE = 2e5 + 10;
const int INF = 0x3f3f3f3f;
int x[SIZE], y[SIZE];
struct Stack
{
int st[SIZE];
int tp;
void clear() { tp = 0; }
void push(int x) { st[++tp] = x; }
int top() { return st[tp]; }
int sec() { return st[tp - 1]; }
void pop() { --tp; }
bool empty() { return tp == 0; }
} stmn, stmx;
struct Laffey
{
#define ls(i) (i << 1)
#define rs(i) (i << 1 | 1)
int l, r;
int mn, cov, add;
Laffey(int l = 0, int r = 0, int mn = INF, int cov = -1, int add = 0) : l(l), r(r), mn(mn), cov(cov), add(add) {}
} tree[SIZE << 2];
void push_up(int i)
{
tree[i].mn = min(tree[ls(i)].mn, tree[rs(i)].mn);
}
void update(int i, int cov, int add)
{
if (cov != -1)
{
tree[i].add = 0;
tree[i].mn = cov;
tree[i].cov = cov;
}
tree[i].add += add;
tree[i].mn += add;
}
void push_down(int i)
{
if (!tree[i].cov)
return;
update(ls(i), tree[i].cov, tree[i].add);
update(rs(i), tree[i].cov, tree[i].add);
tree[i].cov = -1;
tree[i].add = 0;
}
void build(int l, int r, int i)
{
tree[i].l = l, tree[i].r = r;
if (l == r)
return;
int mid = (l + r) >> 1;
build(l, mid, ls(i));
build(mid + 1, r, rs(i));
push_up(i);
}
void Cover(int l, int r, int i, int k)
{
if (l > r)
return;
if (tree[i].l >= l && tree[i].r <= r)
{
update(i, k, 0);
return;
}
push_down(i);
if (tree[ls(i)].r >= l)
Cover(l, r, ls(i), k);
if (tree[rs(i)].l <= r)
Cover(l, r, rs(i), k);
push_up(i);
}
void Add(int l, int r, int i, int k)
{
if (tree[i].l >= l && tree[i].r <= r)
{
update(i, -1, k);
return;
}
push_down(i);
if (tree[ls(i)].r >= l)
Add(l, r, ls(i), k);
if (tree[rs(i)].l <= r)
Add(l, r, rs(i), k);
push_up(i);
}
int query(int i, int k)
{
if (tree[i].l == tree[i].r)
return tree[i].l;
push_down(i);
if (tree[ls(i)].mn <= k)
return query(ls(i), k);
if (tree[rs(i)].mn <= k)
return query(rs(i), k);
return INF;
}
int cnm(int s, int i)
{
if (tree[i].l == tree[i].r)
return tree[i].mn;
push_down(i);
if (tree[ls(i)].r >= s)
return cnm(s, ls(i));
return cnm(s, rs(i));
}
pir comp(pir a, pir b)
{
if (a.first == b.first)
return a.second < b.second ? a : b;
return a.first > b.first ? a : b;
}
int z[SIZE];
map<int, int> t;
int lst[SIZE];
int main()
{
int n, k, d;
cin >> n >> k >> d;
for (int i = 1; i <= n; i++)
{
cin >> x[i];
if (d == 0)
continue;
y[i] = (x[i] % d + d) % d, z[i] = floor(x[i] * 1.0 / d);
lst[i] = t[x[i]];
t[x[i]] = i;
}
if (d == 0)
{
pir ans = {0, INF};
int l = 0, r = 0;
for (int i = 1; i <= n; i++)
{
if (x[i] != x[i - 1])
l = i;
ans = comp(ans, {i - l + 1, l});
}
cout << ans.second << " " << ans.second + ans.first - 1;
return 0;
}
build(1, n, 1);
int last = 1;
pir ans = {0, INF};
for (int i = 1; i <= n; i++)
{
if (y[i] != y[i - 1])
{
Cover(1, i - 1, 1, INF);
stmn.clear();
stmx.clear();
}
Cover(1, lst[i], 1, INF);
Cover(i, i, 1, 0);
Add(1, i, 1, -1);
Add(stmn.top() + 1, i, 1, z[i] - z[stmn.top()]);
Add(stmx.top() + 1, i, 1, z[stmx.top()] - z[i]);
while (!stmn.empty() && z[i] < z[stmn.top()])
Add(stmn.sec() + 1, stmn.top(), 1, z[stmn.top()] - z[i]), stmn.pop();
while (!stmx.empty() && z[i] > z[stmx.top()])
Add(stmx.sec() + 1, stmx.top(), 1, z[i] - z[stmx.top()]), stmx.pop();
int l = query(1, k - 1);
ans = comp(ans, make_pair(i - l + 1, l));
stmn.push(i);
stmx.push(i);
}
cout << ans.second << " " << ans.second + ans.first - 1;
return 0;
}

 test总结
test总结

