简单博弈论

前置知识

IGC游戏

一、定义：

1. 两名选手
2. 两名选手轮流行动，每一次行动可以在有限合法操作集合中选择一个
3. 游戏的任何一种可能的局面(position)，合法操作集合只取决于这个局面本身，不取决于轮到哪名选手操作、以前的任何操作、骰子的点数或者其它因素；局面的改变称为“移动”(move)
4. 如果轮到某名选手移动，且这个局面的合法的移动集合为空（也就是说此时无法进行移动），则这名选手负

 对于第三条，我们有更进一步的定义Position，我们将Position分为两类：

P-position：在当前的局面下，先手必败
N-position：在当前的局面下，先手必胜

N/P性质：

1. 合法操作集合为空的局面是P-position
2. 可以移动到P-position的局面是N-position
3. 所有移动都只能到N-position的局面是P-position

二、步骤

步骤1:将所有终结位置标记为必败点（P点）；
步骤2: 将所有一步操作能进入必败点（P点）的位置标记为必胜点（N点）
步骤3:如果从某个点开始的所有一步操作都只能进入必胜点（N点） ，则将该点标记为必败点（P点） ；
步骤4: 如果在步骤3未能找到新的必败（P点），则算法终止；否则，返回到步骤2。

SG函数

一、定义

任何一个 ICG 游戏都可以通过把每个局面看成一个顶点，对每个局面和它的子局面连一条有向边来抽象成这个“有向图游戏”。下面我们就在有向无环图的顶点上定义 SG(Sprague-Garundy) 函数。

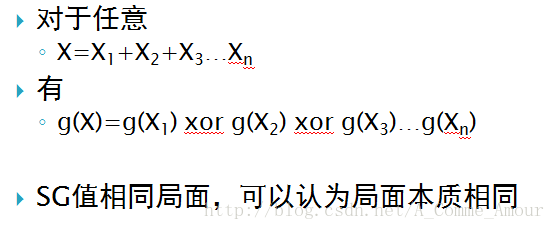
建立

首先定义\(mex(minimal excludant)\)运算，这是施加于一个集合的运算，表示最小的不属于这个集合的非负整数。例如

\[mex{0,1,2,4}=3、 mex{2,3,5}=0、mex{}=0。 \]

对于一个给定的有向无环图，定义关于图的每个顶点的SG函数sg如下：sg(x)=mex{ sg(y) | y是x的后继 }。也就是说，一个点的SG函数为在它所有后继中都未出现的最小的值。

SG值的计算方法：（重点）

1. 可选步数为1~m的连续整数，直接取模即可，SG(x) = x % (m+1);
2. 可选步数为任意步，SG(x) = x;
3. 可选步数为一系列不连续的数，用模板计算。

nim游戏

1. 初始：\(n\)堆

2. 玩法：每次从一堆中选任意扔掉，不可选 \(0\)。

3. 胜负判断：拿走最后的石子\(win\)

做法

性质：对于一个局面，当且仅当A1 xor A2 xor ... xor AN =0时，该局面为P局面。

威佐夫博弈