学案2

前言：这篇虽然真的很水，但真的有在认真对待QwQ

学案2

排序

性质

稳定性

稳定性是指相等的元素经过排序之后相对顺序是否发生了改变。

基数排序、计数排序、插入排序、冒泡排序、归并排序是稳定排序。
选择排序、堆排序、快速排序不是稳定排序。

时间复杂度

oiwiki有

选择排序

oiwiki有

冒泡排序

oiwiki有

插入排序

oiwiki有

计数排序

oiwiki有

基数排序

oiwiki有

快速排序

oiwiki有

归并排序

oiwiki有

堆排序

oiwiki有

桶排序

oiwiki有

希尔排序

oiwiki有

锦标赛排序

oiwiki有

高精

oiwiki有

浅谈STL&高精：懒人利器&一生之敌

说在前头：

这是copy学长的。
考虑到时间是有限的，知识是无限的，会讲得很快。

1. 第二次讲课，把这个课件修了修应该更加接近时代了一些
2. 其实就是想给大家先看看这个才写的这玩意：

1、\(STL\)

​ \(STL\)​是“Standard Template Library”，简单来说就是标准工具库，是C++编译器提供的一套 易用的现成的算法工具.(无感情)

1)、迭代器

​ \(STL\) ​特产，可以理解为指针，它的数据类型定义是这样的

STL类型（包括<>里的东西）::iterator a;//定义一个数据类型为某个STL迭代器的变量为a
STL类型（包括<>里的东西）::const iterator a;//定义一个数据类型为某个STL迭代器的常量为a
STL类型（包括<>里的东西）::reverse_iterator a;//定义一个反向迭代器a	

​ 对\(STL\)的迭代器我们有以下分类：

​ 1.单向迭代器：仅支持对容器向前或向后的单一方向的便利支持对元素的读取，其中正向迭代器大家应该都不陌生，关于反向迭代器的话就是反向，迭代器，没了然后你在遍历的时候

for(vector< int >::reverse_iterator it = vec.rbegin(); it != vec.rend(); it ++)

这就是反向遍历了

​ 2.双向迭代器：支持双向遍历，支持读取

​ 3.随机访问迭代器：支持O（1）复杂度的随机访问，支持读取

​ 但 \(STL\) 与 \(STL\) 之间不能一概而论，部分迭代器之间是有一点区别滴，就在后面讲吧。

​ 对了,首先一定要明确一点:

所有STL的.end()返回的都是最后元素的后一位的迭代器

迭代器失效

​ 这是我在搜一些神奇的东西的时候看到的，下次 \(RE\) 的时候可以往这方面考虑一下（当然你没用迭代器的话就另说了）。
由于不同\(STL\)之间的迭代器不一样，迭代器失效的情况也不尽相同。后面我们会大力分讨仔细叙述一番：

---

2)\(vector\)

​ \(vector\)，不定长数组，是一种基于你数组中元素个数决定空间的东西，不用你去预先开空间，可能会省点空间(也可能二倍开炸你），甚至能拿着玩意氵过某些数据结构的题。

---

\(vector\) 的原理：

​ 我们设当前的 \(vector\) 里有了 \(n\) 个元素，而他已经申请了 \(m\) 的空间，

​ 如果 \(n==m\),那么 \(vector\) 内部就会再申请\(2*m\)的空间,把原来的数挪到这里面,删去原来的空间

​ 如果 \(n<m/4\) ,那么 \(vector\) 内部会释放成 \(m/2\) 的内存

---

​ 构造操作：

// 0. 创建空vector; 常数复杂度
vector<int> v0;
// 1. 这句代码可以使得向vector中插入前3个元素时，保证常数时间复杂度
v0.reserve(3);
// 2. 创建一个初始空间为3的vector，其元素的默认值是0; 线性复杂度
vector<int> v1(3);
// 3. 创建一个初始空间为3的vector，其元素的默认值是2; 线性复杂度
vector<int> v2(3, 2);
// 4. 创建一个v2的拷贝vector v4， 其内容元素和v2一样; 线性复杂度
vector<int> v4(v2);
// 5. 创建一个v4的拷贝vector v5，其内容是{v4[1], v4[2]}; 线性复杂度
vector<int> v5(v4.begin() + 1, v4.begin() + 3);
// 6. 移动v2到新创建的vector v6，不发生拷贝; 常数复杂度; 需要 C++11
vector<int> v6(move(v2));  // 或者 v6 = std::move(v2);

​ 用法应该不用多说，在这就提一嘴吧

#include<vector>//头文件：不过不会还有人不打万能头吧
V.push_back(b);//在数组末尾新加一个元素b 复杂度均摊常数，最坏线性(这种情况似乎并不多见？)
V.size();//读取V数组的元素个数
v.resize();//改变vector的长度，多退少补
v.max_size();//返回vector可能的最大长度
V.pop_back();//删除最后一个元素 常数复杂度
V.push_front(a);//别用，单次操作O（n）的
V.empty();//是否为空
V.clear();//清空数组
V.begin();V.end();//返回第一个元素/末尾元素的迭代器
V.insert(poi,b);//在迭代器poi的位置插入b 复杂度与poi离末尾的距离有关
V.erase(poi);//删除迭代器poi位置的元素 复杂度同insert
V.erase(first,last);//删除迭代器first到迭代器last的元素 复杂度同insert
V.assign(len,val);//将一定长度内存分配给V并初始化其中元素为val
V.reserve(len);//申请重新分配内存（前提是你至少得有len个元素，否则您就等死（RE）吧（无仁慈））
sort(V.begin(),V.end(),cmp);//将V数组按一定规则排序

当我们去 \(\rm OI-Wiki\) 上搜索的时候，我们可以发现这么一段东西：

vector<bool>标准库特别提供了对 bool 的 vector 特化，
每个“bool”只占 1 bit，且支持动态增长。
但是其 operator[] 的返回值的类型不是 bool& 而是 vector<bool>::reference。
因此，使用 vector<bool> 使需谨慎，
可以考虑使用 deque<bool> 或 vector<char> 替代。
而如果你需要节省空间，请直接使用 bitset。

什么意思呢?就是说\(vector\)虽然对\(bool\)进行了特化，他的内存变小了，但是他的返回值也不是一般的\(bool\)了，这就会导致你的一些操作及其印度，一开始是三位数的报错，后来嘛……就没有后来了……

\(update\)：自从我开始学重载后，我甚至见过\(4k+\)的报错……

再\(update\)：今天某乬佬带我见了4.9k+的报错，我人都傻了......

---

关于\(vector\)​的迭代器—随机访问迭代器:

​ 可能是先入为主的观念吧,我觉得它的迭代器是比较常规的(而且极其灵活，及其快乐)

vector<int>::iterator it=V.begin();
int a=*it;//星号解除引用,即迭代器指向的元素,此时a==V[0]
it++;//将迭代器移向下一位
it=it+6;//将迭代器移向下6位
it=vec.end() - vec.begin()//vector支持迭代器之间相减（但不支持相加，返回的是一个difference_type型，你直接当int也没多大问题但还是建议你强转一下
/*如果还有其他的求在场dalao补充*/

---

​ 1.\(vector\)的失效问题

​ 首先明确，\(vector\)存的元素的地址都是连续的，所以当某一位得地址发生改变，后边的也都会改变，具体来讲的话：

(1)使用erase()时指向删除节点之后（包括）的全部迭代器全部失效，但由于erase操作会返回下一个有效的迭代器，用它来初始化删除节点失效的迭代器就行了

(2)push_back()时，先前指向end()的迭代器全部失效

(3)当我们满足了阀值，发生空间重新分配时，所有迭代器全部失效

(4)当我们插入一个元素(insert();push_back（）)时，如果空间未重新分配，指向插入位置之后的迭代器全部失效

---

3)\(set/multiset\)

​ \(set\)​,你可以直接理解为数学里的集合,它同样没有重复元素.和数学集合唯一的区别大概就是内部有序(从小到大),所以你塞进去的类型需要被定义过\(<\)​​.

​ 如果需要存重复元素的话,我们有multiset.

\(set\)​的本质：

​ \(set\)的内部其实是一种效率比较高的 \(rb\_tree\)（红黑树，平衡树的一种）

所以有好多操作都是 \(log\) 级别的

---

\(set\)​の常用操作

set<int > s;
s.insert();//插入
s.erase(iterator);//删除迭代器指向的值
s.erase(frist,second);//删除迭代器first和second之间的所有值
s.erase(value);//删除值为value的元素，记得删之前康康合法不合法
s.find(value);//查找值为value的迭代器，不存在返回.end()
s.count(value);//value是否出现过
s.begin();
s.end();
s.clear();//清空
s.empty();//是否为空
s.max_size();//返回能承载的最大元素
s.size();//返回元素个数
s.rbegin();//返回反转后的begin C++11
s.rend();//返回反转后的end C++11
s.lower_bound(x);//set内部的log级别
s.upper_bound(x);//set内部的log级别

关于最大元素，我从\(\rm C++ Referece\)看到的是这玩意：

This is the maximum potential size the container can reach due to known system or library implementation limitations, but the container is by no means guaranteed to be able to reach that size: it can still fail to allocate storage at any point before that size is reached.

翻译一下：

​ 这是由于已知的系统或库实现限制，容器可以达到的最大潜在大小，但是容器并不能保证能够达到该大小：在达到该大小之前，它仍然可能无法在任何时候分配存储。

至于有啥用，你感性理解一下？

---

\(multiset\)の常用操作:

​ set能用的东西multiset都能用，那其实就一个定义了，还有几个不一样的我下面也会写

multiset<类型名> sm;
sm.erase(value);//删除所有等于value的元素
sm.count(value);
/*其实上面的.count()返回的是set中等于value的元素的个数
但是因为set不重，所以返回的只有0/1
而这个就是真正的“等于value的元素的个数”了*/

---

\(multiset，set\)​​の迭代器—双向访问迭代器：

​ 不支持随机访问，支持型号解除引用，仅支持++和--两个符号进行移动，支持==和!=进行比较

​ 还有一个比较好玩的点，是关于 insert 的返回值问题，insert 这个东西吧，他就很神奇，他长这样：

pair< set< type_name >,  bool > insert(const value_type& val);

​ 换言之，他返回的是一个 \(pair\)，其中first 指的是你插入位置的迭代器，second 返回的是一个 bool 变量

代表你是否成功的插入（没跟之前的重复），同时，他返回的是一个 const，嗯？提这个干嘛？你知道有个东西他叫 珂朵莉树 吗

4)\(map\)

官方定义：

​ \(map\)是关联容器，用于存储由键值和映射值组合而成的元素，并遵循特定顺序。

换句话说\(map\)就是一个\(key->value\)的单向映射关系

​ \(key\)就是下标，我们称他为键值，\(value\)就是下标的对应值

​ 它的内部也是一棵\(rb\_tree\)。

---

\(map\)の常用操作:

map<key_type,val_type >;
m[key];//map的随机调用（伪），复杂度log级的
m.insert();//插入
m.erase(iterator);//删除迭代器指向的值
m.erase(first,second);//删除迭代器first和second之间的所有值
m.erase(key_value);//删除键值为key_value的元素，记得删之前康康合法不合法
m.find(key_value);//查找键值值为key_value的迭代器，不存在返回.end()
m.count(key_value);//键值key_value是否出现过，因为非重，所以也是0/1
m.begin();
m.end();
m.clear();//清空
m.empty();//是否为空
m.max_size();//返回能承载的最大元素
m.size();//返回元素个数
m.rbegin();//返回反转后的begin
m.rend();//返回反转后的end
m.equl_range(int key);//返回的是pair<iterator, iterator>, 前一个等价于lower_bound()，后一个等价于upper_bound()，返回的是键值等于key的键值对的范围
m.emplace();//insert plus

值得注意的是，map的键值对的键值是可能相同的，所以他的一个 key 可以对应一堆的 val
其实\(map\)的操作和\(set\)的操作十分类似 毕竟sm是一对嘛

---

\(map\)​の迭代器—双向访问迭代器：

​ 我们的\(map\)的迭代器其实是一个\(pair\)，例如：

map<int,int >::iterator it;
it=m.begin();
it->first;//key_value
it->second;//value

---

5）\(unordered\_map\)

​ c++11现在可以用了，来提一提 \(unordered\_map\)， 这东西是基于 \(hash\) 的对吧

那我们就可以用这个东西来优化自己的判重之类的东西，可以从 map 的 O(log) 级别变成期望 O(1)。

​ 但是啊，很印度的事情来了，unordered_map ，他是我看见的第一个使用 前向迭代器 的东西，就是说他只能用 *it, ++it, it++ 三个运算……

​ 操作也不多，就几个：

unordered_map< int, int > mp;
mp.begin();
mp.end();
mp.find();

Warning： 既然这东西是基于 hash 的，那他就会有一定概率发生 hash 冲突，然后你的 unordered_map 就会变成 O(n^2)+ 了……

---

还有两个东西我没讲:

​ \(multimap\)（我不知道这玩意有啥用）

​ \(unordered\_set\)(c++11,基于hash)

​ 有兴趣的自己康康吧

---

\(map,set,multimap,multiset\)的迭代器失效问题：
因为他们都是关联式容器（key-val），所以甚至没有区别，erase()之后只有被删除元素的迭代器失效，解决方案：用完之后迭代器自增（++），或者erase() 返回他更新后的迭代器，直接赋个值就行

6)\(queue/PQ/deque/stack\)

​ 把这一坨东西放在一起讲是因为操作和原理及其类似，我们放在一起讲

---

​ 首先我们得明确一点，\(queue\)、\(PQ\)、\(stack\)都属于容器适配器，而\(deque\)不是(我绝对不会告诉你我是因为之前不知道才把他们写在一起的)

​ \(C++\)中的容器适配器是干什么的呢？我们已有容器（比如\(vector\)、\(list\)、\(deque\)），他们支持的的操作很多，比如插入，删除，迭代器访问等等。而我们希望这个容器表现出来的是栈的样子：先进后出，入栈出栈等等，此时，我们没有必要重新动手写一个新的数据结构，而是把原来的容器重新封装一下，改变它的接口，就能把它当做栈使用了。

​ 但对于我们来说用到更多的是他们自带的底层容器，无需更改

​ stack的底层容器是deque

​ queue的底层容器是deque

​ priority_queue的底层容器是vector

​ \(queue\)和\(PQ\)大家都用过(你已知的所有操作就是\(queue\)能用的所有操作了，真的)，这里不再多讲

​ quque&qriority_queueの构造：

queue<TypeName> q;  // 使用默认底层容器 deque，数据类型为 TypeName
queue<TypeName, Container> q;  // 使用 Container 作为底层容器
queue<TypeName> q2(q1);  // 将 s1 复制一份用于构造 q2
priority_queue<TypeName> q;             // 数据类型为 TypeName
priority_queue<TypeName, Container> q;  // 使用 Container 作为底层容器
priority_queue<TypeName, Container, Compare> q;
// 使用 Container 作为底层容器，使用 Compare 作为比较类型

// 默认使用底层容器 vector
// 比较类型 less<TypeName>（此时为它的 top() 返回为最大值）
// 若希望 top() 返回最小值，可令比较类型为 greater<TypeName>
// 注意：不可跳过 Container 直接传入 Compare

​ 还有之前在打\(heap_dij\)的时候大家有用过这么一个玩意：

#define pair<int,int > P
qriority_queue<P,vector<p > ,greater<P > >;

其实就是上面这一行的体现：

priority_queue<TypeName, Container, Compare> q;

​ 有一个点得注意一下，因为\(PQ\)内部已经不满足\(FIFO\)了，所以\(queue\)的队首元素是q.front();而PQ是pq.top();，还有\(PQ\)里面没有.clear(),\(PQ\)里面有两个\(log\)级别的操作，分别为push()&pop()

---

​ 构造操作：

stack<TypeName> s;  // 使用默认底层容器 deque，数据类型为 TypeName
stack<TypeName, Container> s;  // 使用 Container 作为底层容器
stack<TypeName> s2(s1);        // 将 s1 复制一份用于构造 s2

​ \(stack\)的话其实就是一个栈，操作也很简单

stack<int > stk;
stk.push();
stk.top();
stk.size();
stk.empty();
stk.pop();

​ 什么？这三个东西的迭代器？哦对了，它仨没有迭代器,(呵，躯壳而已)

---

​ 接下来是重头戏，\(deque\)！！！

​ \(deque\)是一个双端队列，什么意思呢，我可以从两端调用！！！

​ 构造操作:

// 1. 定义一个int类型的空双端队列 v0
deque<int > v0;
// 2. 定义一个int类型的双端队列 v1，并设置初始大小为10; 线性复杂度
deque<int > v1(10);
// 3. 定义一个int类型的双端队列 v2，并初始化为10个1; 线性复杂度
deque<int > v2(10, 1);
// 4. 复制已有的双端队列 v1; 线性复杂度
deque<int > v3(v1);
// 5. 创建一个v2的拷贝deque v4，其内容是v4[0]至v4[2]; 线性复杂度
deque<int > v4(v2.begin(), v2.begin() + 3);
// 6. 移动v2到新创建的deque v5，不发生拷贝; 常数复杂度; 需要 C++11
deque<int > v5(std::move(v2));

​ 常规操作：

deque<int > dq;
dq.begin();
dq.end();
dq.front();//返回前端元素
dq.back();//返回后端元素
dq.push_front();//把一个东西塞到前端
dq.push_back();//把一个东西塞到后端
dq.insert(poi,val);//在迭代器poi位置插入val
dq.insert(poi,n,val);//在迭代器poi位置插入n个val
dq.insert(poi.firat,last);//在迭代器poi后插入迭代器first到迭代器last的所有元素的拷贝
dq.erase(it);//删除迭代器it引用的值
dq.erase(first,last);//删除迭代器first到迭代器last的所有值
dq.clear()//清空
dq[poi];//这是我最喜欢dq的一点了，就像数组一样调用poi位置的值

\(deque\)的迭代器—随机访问迭代器：

​ 支持==和！=比较，支持++ --移动，支持*解除引用，支持[]随机访问调用

---

\(deque\)的迭代器失效

(1)插入元素时全部迭代器失效(其实在队首插入还是有些不同的)

(2)在队首队尾删除时只有末尾迭代器失效

7)\(bitset\)

​ \(bitset\)就是一个二进制数，但是存在了一个类似于数组的结构里，而且数组每一位都是0/1，占1bit

\(bieset\)的定义:

bitset<10000> a;//定义a为一个10000位的二进制数

bitset的构造有四种:

bitset<4> bitset1;　　//无参构造，长度为4，默认每一位为0
bitset<8> bitset2(12);　　//长度为8，二进制保存，前面用0补充
string s = "100101";
bitset<10> bitset3(s);　　//长度为10，前面用0补充
char s2[] = "10101";
bitset<13> bitset4(s2);　　//长度为13，前面用0补充

bitset的常见操作:

bitset<4> b1(string("1001"));
bitset<4> b2(string("0110"));
b1^=b2;
b1&=b2;
b1|=b2;
b1<<=2;
b1>>=1;
~b2;
b1==b2;
b1!=b2;
b1&b2;
b1|b2;
b1^b2;
/*经典的二进制位运算bitset都可以干*/
b1.count();//返回1的个数
b1.size();//求bitset的大小
b1.test();//查位置为poi的数0/1，返回false/true
b1.any();//是否有1 true/false
b1.none();//是否没有1 true/false
b1.all();//是否全部为1 true/false
b1.set();//所有位全部初始化为1
b1.set(poi);//讲poi位赋值为1
b1.reset();//所有位全部初始化为0
b1.reset(poi);//poi位赋值为0
b1.to_ulong();//转化为十进制(unsigned long)
b1.to_string();//转化为字符串(string)

---

8)垃圾佬最爱的\(<algorithm>\)

​ 这个东西就很神奇，这个头文件里总能找到一些用起来很舒服的东西。
​ 像sort啊,kth-number()啊,就很实用(某种意义上)
​ 这感觉就像在捡垃圾(Lg倒了我真难受TAT)
​ 但其实大家常用的也就这么几个，你去C++ Reference上也刨不出来啥了，提一嘴就过吧
​ 常用操作:

reverse(first,last);//区间反转
/*剩下的我感觉没啥了，详情请见C++ Reference -> <algorithm> */

9) \(Array\)

\(Array\) 是一个听起来很……高级的一个东西，然后你把这个词扔到百度翻译上去：

…………………………………………………………

但是这东西我既然讲了就一定有他的好处对吧，那就听我接着 bb 吧

\(Array\) 是一个 c++11 的新容器，初始分配内存，支持随机调用

直接上操作：

Array<type_name, 100> c;//定义一个Array c,里面的元素初始随机
Array<type_name, 100> c = {};//定义一个Array c，初始元素赋为0
Array<type_name, 100> c = {42};//定义一个Array c
Array<type_name, 100> c(c1);拷贝构造,大家都懂
c[idx] = 10;//数组赋值
c.at(idx) = 10;//指针人狂喜
c.front();//看图说话
c.back();//看图说话
c.begin() / end() / rbegin() / rend() / cbegin()/ cend() / crbegin() / crend();

接下来我们来说说这玩意到底有啥用

首先你可以用指针，然后扔掉中括号（bushi）

之后，array 这个东西可以放在其他 STL 中，比如你想拿vector + 定长的数组，你可以这样：

vector< array< int, 1000> >

其他的STL也同理，而且他 不用重载小于号

10) \(Tuple\)

\(Tuple\) ，这个玩意听起来很新奇啊（其实我也noip之后才学的）

他是有中文名字的，他叫 元组（我听到了PY党 && C# 党暴起的声音）

简单来讲，这个东西就是一个paiaiaiaiaiaiaiaiaiaiaiaiaiaiaiaiaiaiaiaiaiair

就是说，它是用来保存元素集合的对象，而且元素可以是不同类型

构造也比较类似：

tuple<string, size_t> t1;
tuple<my_struct, string> t2 {my_struct{...}, string{"F**k CCF"}};
tuple<my_struct, string> t2_copy {t2};
tuple<string, string, string> t3 {"F**k", "CCF", "wrnm"};
tuple<string, string> t4 = make_tuple("ccf", "nmsl");

当然我们还可以用 \(pair\) 来构造 \(tuple\)：

auto pair_ = make_pair("f**k", "ccf");
tuple<string, string> TU {pair_};
tuple<string, string> thu{pair<string, string> {"f**k", "ccf"}}

那这样的话就有了另一个问题：我们的 pair 因为只有两个参，所以才有了first 和 second ，但是tuple 这个东西，他是有一堆参数的……这个时候就又有了两个函数来辅助操作：get<>() 和 tie<>()

get<>() 的话有两种使用，一种是基于元素的：

get<0>(a);//返回tuple的第一个元素

第二种是根据类型，但要求这个类型在tuple 中只出现了一次，但是他很玄学，不推荐使用

tie<>() 的用法很简洁：

auto thu = make_tuple(string{"ccf"}, 114514, 'c', 11.2);
string str;
int a;
char ch;
double aa;
tie(str, a, ch, aa) = thu;

简洁明了，一目了然

11) \(\_\_gnu\_pbds\)

大的来了

__gnu_pbds 实际上是一个 namespace，内部封装了Trie, Tree, Hash,priority_queue 等数据结构

首先我们需要一段前摇：

#include<ext/pb_ds/assoc_container.hpp>
#include<ext/pb_ds/tree_policy.hpp>//用tree
#include<ext/pb_ds/hash_policy.hpp>//用hash
#include<ext/pb_ds/trie_policy.hpp>//用trie
#include<ext/pb_ds/priority_queue.hpp>//用priority_queue
using namespace __gnu_pbds;

太烦了吧！！！如果我全都用的话，你想怎么办？

答案是有的：

#include<bits/extc++.h>
using namespace __gnu_pbds;
//bits/extc++.h与bits/stdc++.h类似，bits/extc++.h是所有拓展库，bits/stdc++.h是所有标准库

但是！这是 \(Linux\ only\) ！！！因为windows 环境下会少一个头文件（各位大佬可以试试把 Linux 的头搬过来试试）

hash

这个 hash 全名是 hash_table 用法和map类似，但是他常数极其优秀（这也是平板电视的特质）

操作的话：

cc_hash_table< string, int > ha;//拉链法
gp_hash_table< string, int > hh;//探测法，似乎会更快一些

然后用到最多的大概就是 [] 和 find() 了，没了

tree

大的来了

这里的 tree 指的就是 平衡树 ，其中有 rb_tree, splay_tree, ov_tree 其中 rb_tree 是最快的。

#define pii pair< int, int > 
#define mp(a, b) make_pair(a, b)
tree< pii, null_type, less<int>, rb_tree_tag, tree_order_statistics_node_update> tr;
//数据类型，无映射，排序方式，树的类型，更新方式(为了支持查询第k大和排名的值)
tr.insert(mp(x,y)); //插入;
tr.erase(mp(x,y)); //删除;
tr.order_of_key(pii(x,y)); //求排名 
tr.find_by_order(x); //找k小值，返回迭代器 
tr.join(b); //将b并入tr，前提是两棵树类型一样且没有重复元素 
tr.split(v,b); //分裂，key小于等于v的元素属于tr，其余的属于b
tr.lower_bound(x); //返回第一个大于等于x的元素的迭代器
tr.upper_bound(x); //返回第一个大于x的元素的迭代器

而且这个东西他也不支持插入相同元素，所以可以用个pair 或自定义结构体或者用long long 和 double 整个hash来搞

Trie

字典树，这玩意手写就行了（摆了摆了）

剩下的还又一些杂七杂八的 特别NB 的，我就先不说了，感兴趣的可以去看看 日爆

12) \(rope\)(G++ only)

rope，这东西我也说不上来他到底是个啥，就很奇怪

他是块链的底层实现，但是但本来是作为超级string存在

但是我们还可以拿他可持久化线段树等……

首先如果想声明一个 rope 我们需要一个头和一个命名空间：

#include<ext/rope>
using namespace __gnu_cxx;

然后构建的话是这样的：

rope< int > rp;
rope< long long > lp;
rope< char > cp;
crope crp; // 等价于rope<char> crp;
rope< doouble> db;
//rope里面不能嵌套STL

操作的话我们为了方便区分，所以我们根据定义类型不同分为两部分

1. crope / rope<char> ：

append(string &s,int pos,int n);//将一个字符串的pos位之后的n位放进rope的后面
substr(int pos, int len);//提取从pos之后的len个字符
at(int x);//访问下标为x的元素
erase(int pos, int num);//从pos开始，删除num个字符
copy(int pos, int len, string &s);//从rope的下标pos开始的len个字符用字符串s代替，如果pos后的位数不够就补足
replace(int pos, string &x);//从rope的下标pos开始替换成字符串x，x的长度为从pos开始替换的位数，如果pos后的位数不够就补足

2. rope<others>

insert(int pos, int *s, int n);//将int数组（以下的s都是int数组）s的前n位插入rope的下标pos处，如没有参数n则将数组s的所有位都插入rope的下标pos处

append(int *s,int pos,int n);//把数组s中从下标pos开始的n个数连接到rope的结尾，如没有参数n则把数组s中下标pos后的所有数连接到rope的结尾，如没有参数pos则把整个数组s连接到rope的结尾

substr(int pos, int len);//提取rope的从下标pos开始的len个数

at(int x);//访问rope的下标为x的元素

erase(int pos, int num);//从rope的下标pos开始删除num个数

copy(int pos, int len, int *s);//从rope的下标pos开始的len个数用数组s代替，如果pos后的位数不够就补足

replace(int pos, int *x);//从rope的下标pos开始替换成数组x，x的长度为从pos开始替换的位数，如果pos后的位数不够就补足

那怎么那他写可持久化线段树呢？简单！暴力就行了！

时间复杂度 \(O(n \sqrt n)\)，这样的话时间复杂度

而在可持久化的优势空间复杂度上，rope是 \(O(玄学)\) 的。

---

\(STL\)的题我找不到多少，所以就给大家整来了可以用STL水的题

P2234 营业额统计（平衡树（×）set（√））

P1486 郁闷的出纳员（平衡树（×）vector（√））

P3850 书架（平衡树（×）vector（√））

---

--------------------------------------------------------------分界线----------------------------------------------------------------------

2、高精来了！！！

我先说一嘴:

\(\Huge\rm Python\)​​是世界上最好的语言

后来某dalao看见了，他让我再添上一句：

人生苦短，我学\(\Huge\rm Python\)​

关于高精：

我们为什么需要它？

因为我们C++中最长的 unsigned long long 也只有2⁶⁴面对特大的数据范围(10¹⁰⁰⁸⁶)直接傻眼，我们又不能拿\(Python\)去打表（好像可以？我的电脑里就有前朝遗物$ P\ Y\ 3\ .\ 7$），所以才有了这么一个东西。

1)常规高精

就是模拟你小学手算的过程，我们拿一个式子举例：

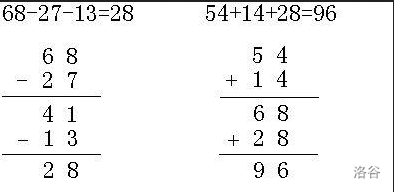
就这么乱搞就可以了

一开始我的代码里是没有高精除高精的(感谢小鸟游先生提供素材)：

而且我抱着认真负责 为省事找理由 的态度，我还特意去搜了一下，结果发现了这个：

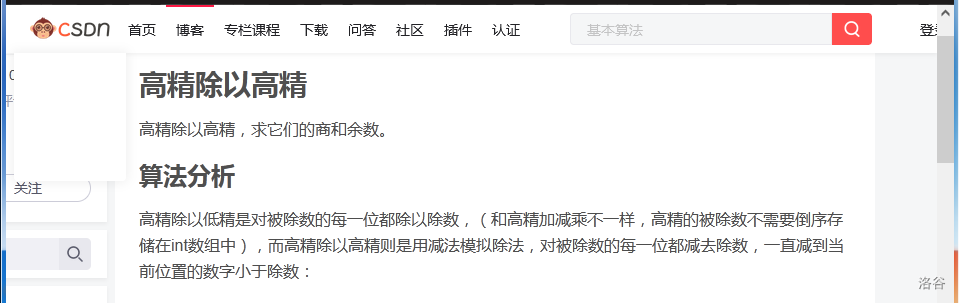
好嘛，\(\Huge直接连减就完事了\)​​​​​​​,于是就有了代码里的高精除高精实现

代码：

#include<bits/stdc++.h>
using namespace std;

string str1,str2;
bool flag;
vector<int > a,b,ans;
vector<int > anss;

void turnn(string s,vector<int > &v)
{
	int len=s.length()-1;int c;
	for(int i=len;i>=0;i--)
	{
		c=int(s[i]-'0');
		v.push_back(c);
	}
}
bool lless(vector<int > v1,vector<int > v2)//<
{
	if(v1.size()!=v2.size()) return (v1.size()<v2.size());
	for(int i=0;i<v1.size();++i)
	{
		if(v1[i]!=v2[i]) return (v1[i]<v2[i]);
	}
	return false;
}
bool more(vector<int > v1,vector<int > v2) {return lless(v2,v1);}//>
bool nless(vector<int > v1,vector<int > v2) {return !lless(v1,v2);}//>=
bool nmore(vector<int > v1,vector<int > v2) {return !lless(v2,v1);}//<=
bool equa(vector<int > v1,vector<int > v2) {return !lless(v1,v2)&&!lless(v2,v1);}//==
bool nequal(vector<int > v1,vector<int > v2) {return lless(v1,v2)||lless(v2,v1);}//!=
vector<int > add(vector<int > v1,vector<int > v2)
{
	vector<int > v3;
	int maxx=max(v1.size(),v2.size());
	int g=0;
	for(int i=0;i<maxx;++i)
	{
		int x=0;
		if(i<v1.size()) if(v1[i]) x+=v1[i];
		if(i<v2.size()) if(v2[i]) x+=v2[i];
		if(g) x+=g;
		g=x/10;x%=10;
		v3.push_back(x);
	}
	if(g) v3.push_back(g),g=0;
	while(v3.size()>1&&!v3.back()) v3.pop_back();
	return v3;
}
vector<int > sub(vector<int > v1,vector<int > v2)
{
	vector<int > v3;
	if(lless(v1,v2))
	{
		flag=1;swap(v1,v2);
	}
		int g=0;
	for(int i=0;i<v1.size();i++)
	{
		int x=0;
		if(i<v1.size()) x+=v1[i];
		if(i<v2.size()) x-=v2[i];
		if(g) x-=g;
		if(x<0)
		{
			g=1;
			if(i<v1.size()) x+=10;
		} 
		else g=0;
		v3.push_back(x);
	} 
	while(v3.size()>1&&!v3.back()) v3.pop_back();
	if(flag) v3[v3.size()-1]=-v3[v3.size()-1];
	return v3;
}
vector<int > mul(vector<int > v1,vector<int > v2)
{
	vector<int > v3;
	if(str1=="0"||str2=="0")
	{
		v3.push_back(0);return v3;
	}
	if(v1.size()<v2.size()) swap(v1,v2);
//	v3.resize(v2.size()+v1.size());
	v3.assign(v2.size() + v1.size(),0);
	for(int i=0;i<v1.size();i++)
	{
		for(int j=0;j<v2.size();j++)
		{
			v3[i+j]+=v1[i]*v2[j];
		}
	}
	for(int i=0;i<v3.size();i++)
	{
		if(v3[i]>9)
		{
			v3[i+1]+=v3[i]/10;
			v3[i]%=10;
		}
	}
	while(v3.size()>1&&!v3.back()) v3.pop_back();
	return v3;
}

vector<int > dvi(vector<int > v1,vector<int > v2)
{
	int tim =0;
	while(more(v1,v2));
	v1=sub(v1,v2);
	return v1;
}

vector<int > mul_(vector<int > v1,long long num)
{
	vector<int >v3;
	int g=0;
	for(int i=0;i<v1.size() || g;i++)
	{
		if(i<v1.size()) g+=v1[i]*num;
		v3.push_back(g % 10);
		g/=10;
	}
	while(v3.size()>1 && !v3.back()) v3.pop_back();
	return v3;
} 

vector<int > dvi_(vector<int > v1,long long num,long long &r)
{
	vector<int > v3;
	r=0;
	for(int i=v1.size()-1;i>=0;i--)
	{
		r=(r<<1)+(r<<3)+v1[i];
		v3.push_back(r/num);
		r=r%num;
	}
	reverse(v3.begin(),v3.end());
	while(v3.size()>1&&!v3.back()) v3.pop_back();
	return v3;
}

void prin(vector<int > v)
{
	vector<int >::iterator it=v.end()-1;
	if(v.size()>1) while(*it==0) it--;
	for(it;it>=v.begin();it--) cout<<*it;
}

int n;
long long bb,res;
string s1;
vector<int > aa; 

int main()
{
	
	string s1;
	cin >> s1 >> bb;
	turnn(s1,aa);
	prin(dvi_(aa,bb,res));
	return 0;
}

2)压位高精

其实我们并没有必要一位一位的搞

所以我们可以考虑分块(误)

把他按一定位数截开，然后在搞事

code：

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int mec=1e4;
int c[140001],num,d[140001],s[180002],lt[140001],e[140001],f[140001]={1,1};
bool tc,td;
char a[150001],b[150001];
void sum(int c[],int d[]);
void dec(int c[],int d[]);
void mul(int c[],int d[]);
void div(int c[],int d[]);
int tpow(int n)
{
	int m=10;
	while(--n)
		m*=10;
	return m;
}
void ly(int c[],int n)
{
	int m=n%4;
	n/=4;
	c[0]+=n;
	for(int i=c[0];i>n;--i)
		c[i]=c[i-n];
	for(int i=n;i;--i)
		c[i]=0;
	if(m)
	{
		m=tpow(m);
		for(int i=n+1;i<=c[0];++i)
		{
			c[i]*=m;
			if(c[i-1]>=mec)
			{
				c[i]+=c[i-1]/mec;
				c[i-1]%=mec;
			}
		}
	}
	if(c[c[0]]>=mec)
	{
		c[++c[0]]=c[c[0]-1]/mec;
		c[c[0]-1]%=mec;
	}
	while(c[c[0]]==0&&c[0]) --c[0];
}
void ry(int c[],int n)
{
	int m=n%4;
	n/=4;
	c[0]-=n;
	for(int i=1;i<=c[0];++i)
		c[i]=c[i+n];
	for(int i=c[0]+1;i<=c[0]+n;++i)
		c[i]=0;
	if(m)
	{
		m=tpow(m);
		for(int i=1;i<=c[0];++i)
		{
			c[i]/=m;
			if(c[i]<=mec)
				c[i]+=c[i+1]%m*mec/m;
		}
	}
	if(c[c[0]]>=mec)
	{
		c[++c[0]]=c[c[0]-1]/mec;
		c[c[0]-1]%=mec;
	}
	while(c[c[0]]==0&&c[0]) --c[0];
}
int cmp(int c[],int d[])
{
	if(c[0]<d[0]) return -1;
	else if(c[0]>d[0]) return 1;
	else
	{
		for(int i=c[0];i;--i)
			if(c[i]>d[i]) return 1;
			else if(c[i]<d[i]) return -1;
	}
	return 0;
}
void cpy(int c[],int d[])
{
	for(int i=c[0];i>d[0];--i)
		c[i]=0;
	for(int i=0;i<=d[0];++i)
		c[i]=d[i];
}
void cler(int s[])
{
	for(int i=s[0];i;--i) s[i]=0;
	s[0]=1;
}
void check(int c[])
{
	printf("%d",c[c[0]]);
	for(int i=c[0]-1;i;--i)
		printf("%04d",c[i]);
	puts("");
}
void init()
{
	scanf("%s%s",a,b);
	if(a[0]=='-') tc=1;
	if(b[0]=='-') td=1;
	for(int i=strlen(a)-1;i>=0;--i)
	{
		if(num%4==0&&a[i]!='-')
		{
			c[++c[0]]=a[i]-'0';
			int pw=10;
			for(int j=1;j<4&&i-j>=0&&a[i-j]!='-';++j)
			{
				c[c[0]]+=(a[i-j]-'0')*pw;
				pw*=10;
			}
		}
		++num;
	}
	num=0;
	for(int i=strlen(b)-1;i>=0;--i)
	{
		if(num%4==0&&b[i]!='-')
		{
			d[++d[0]]=b[i]-'0';
			int pw=10;
			for(int j=1;j<4&&i-j>=0&&b[i-j]!='-';++j)
			{
				d[d[0]]+=(b[i-j]-'0')*pw;
				pw*=10;
			}
		}
		++num;
	}
}
void write(int s[])
{
	printf("%d",s[s[0]]);
	for(int i=s[0]-1;i;--i)
		printf("%04d",s[i]);
	puts("");
}
void sum(int c[],int d[])
{
	if(tc&&td)
	{
		putchar('-');
		tc=td=0;
	}
	else if(tc)
	{
		tc=0;
		dec(d,c);
		return;
	}
	else if(td)
	{
		td=0;
		dec(c,d);
		return;
	}
	cler(s);
	s[0]=max(c[0],d[0]);
	for(int i=1;i<=s[0];++i)
	{
		s[i]=c[i]+d[i];
		if(i>1&&s[i-1]>=mec)
		{
			s[i]+=s[i-1]/mec;
			s[i-1]%=mec;
		}
	}
	if(s[s[0]]>=mec)
	{
		s[++s[0]]=s[s[0]-1]/mec;
		s[s[0]-1]%=mec;
	}
}
void dec(int c[],int d[])
{
	if(tc&&td)
	{
		td=0;
		dec(d,c);
		return;
	}
	else if(td)
	{
		td=0;
		sum(c,d);
		return;
	}
	else if(tc)
	{
		putchar('-');
		tc=0;
		sum(c,d);
		return;
	}
	cler(s);
	s[0]=max(c[0],d[0]);
	if(cmp(c,d)<0)
	{
		swap(c,d);
		putchar('-');
	}
	for(int i=1;i<=s[0];++i)
	{
		s[i]+=c[i]-d[i];
		if(s[i]<0)
		{
			s[i]+=mec;
			--s[i+1];
		}
	}
	while(s[s[0]]==0&&s[0]>1)
		--s[0];
}
void mul(int c[],int d[])
{
	if(tc^td)
	{
		putchar('-');
		tc=td=0;
	}
	cler(s);
	s[0]=c[0]+d[0]-1;;
	for(int i=1;i<=c[0];++i)
	{
		for(int j=1;j<=d[0];++j)
		{
			s[i+j-1]+=c[i]*d[j];
			if(i+j-1>1&&s[i+j-2]>=mec)
			{
				s[i+j-1]+=s[i+j-2]/mec;
				s[i+j-2]%=mec;
			}
		}
		if(s[i+d[0]-1]>=mec)
		{
			s[i+d[0]]=s[i+d[0]-1]/mec;
			s[i+d[0]-1]%=mec;
		}
	}
	if(s[s[0]+1]) ++s[0];
}
void div(int c[],int d[])
{
	if(tc^td)
	{
		putchar('-');
		tc=td=0;
	}
	cpy(e,d);
	int la=strlen(a)-tc,lb=strlen(b)-td;
	if(strlen(a)>strlen(b))
	{
		ly(e,strlen(a)-strlen(b));
		ly(f,strlen(a)-strlen(b));
	}
	while(cmp(c,d)>=0)
	{
		while(cmp(c,e)>=0)
		{
			dec(c,e);
			cpy(c,s);
			sum(lt,f);
			cpy(lt,s);
		}
		ry(e,1);
		ry(f,1);
	}
	if(lt[0]==0) lt[0]=1;
	write(lt);
	write(c);
}
void Fpow(int c[],int d[])
{
	lt[1]=lt[0]=1;
	while(d[1]>0||d[0]>1)
	{
		if(d[1]&1)
		{
			mul(lt,c);
			cpy(lt,s);
		}
		mul(c,c);
		cpy(c,s);
		for(int i=1;i<=d[0];++i)
		{
			d[i]=(d[i]+d[i+1]*mec)>>1;
		}
		while(d[d[0]]==0&&d[0]>1) --d[0];
	}
	write(lt);
}
int main()
{
	init();
//	sum(c,d);
//	write(s);
//	dec(c,d);
//	write(s);
//	mul(c,d);
//	write(s);
//	div(c,d);
//	Fpow(c,d);
//	cler(s);
//	write(s);
//	ry(c,5);
//	check(c);
//	ly(d,5);
//	check(d);
	return 0;
}

顺便我来讲一下重载

重载运算符

A.为什么重载？ Ans:为了让某些好用的东西被我自己的类(\(class\))所继承:举个栗子，我们想对我们的\(class\)数组进行排序，又懒得手写快排，这个时候我们直接一波重载小于号，我们就可以直接\(sort\)了~

B.How to 重载

Ans: operator,具体格式就是：

返回类型 operator 运算符(已有的) (const) (传参)
{
    与函数的操作基本无异了。
}

中间还有一些比较好V♂A♂N的东西，边看代码边聊。

3)bitset重载（如果我讲之前学明白了就干）

前方极度不适警告！！！

我们换一个思路

你用的int，long long，之类的其实都是基于二进制

而我们的STL恰好提供了一个存二进制数的东西——bitset

所以我们可以考虑用这玩意搞事情

这个东西有什么优点呢 ：

1.他是直接用bit存储的空间小的雅痞

2.他的枚举会比压位少很多，时间会更优（指加减及极大数据

那这个东西有什么缺点呢：

1.难写

2.长度是固定的

4)课下

题单里有板子和一些历史遗留故事（国王游戏），有一道kruscal的加法需要注意（高精度犯难）。

结束

或是

下一个开始？

题题题

学案1说的好玩的题（也就一道）：
P1084